2. 北京博鼎诚工程设计有限公司, 北京 100012
2. Beijing bodingchen Engineering & Design Co., Ltd, Beijing 100012, China
随着风力发电的渗透率不断增加,风电系统与电网之间的相互影响越来越大,电网公司要求风电机组在电网故障情况下能够按照电网规程继续并网运行,实现故障穿越[1-3]。永磁同步风电机组的发电机定子经全功率AC-DC-AC变流器与电网相接,发电机和电网不存在直接耦合,较其他类型的风电机组相比,电网故障对其影响更小[3],成为未来风电发展的重要方向。
由于电网故障以不对称情况居多,因而风电机组不对称故障穿越的研究具有重要的实际意义[4]。现有文献针对永磁同步风力发电机组实现故障穿越的研究,主要以对称故障情况居多[2, 3, 5-10]。不对称故障时,因网侧电压突然减小,由于PMSG风电机组中并网变流器的限流作用,机组并网功率将减小,而输入机械功率近似不变,这会导致交直交全功率变换器的“有功不平衡”,进而产生变换器直流母线电压升高等问题[6-7]。另外,不对称故障时,电网电压负序分量将带来并网负序电流和交直交换流器直流母线电压2倍工频波动等问题[5]。针对有功不平衡问题,可以采用和对称故障时相类似的故障穿越方法[6-7]。而不对称故障所产生的网侧负序电流和直流母线2倍工频纹波,会对电网运行和变流器自身的工作产生影响,因此期望在机组故障穿越期间,能够同时消除并网负序电流和直流侧母线2倍工频纹波[5, 9]。目前报道的方法有通过改变网侧变换器的控制策略,使其输出三相电流对称,从而减小不对称故障情况下网侧换流器并网电流中的负序分量[8-9],但是交直交换流器直流母线电压仍存在2倍工频波动。也有研究工作在并网电流中人为注入一定比例的负序分量实现并网功率平衡来减小直流母线2倍工频纹波[5, 10],但这以注入电网负序电流为代价。
为了平滑风电机组输出功率的波动,各种储能方法在风电中的应用受到广泛研究[11-15]。其中超级电容器因具有功率密度高、循环寿命长等优点,在平抑风电场输出功率高频段部分的波动上具有良好的应用前景,目前已有文献研究利用超级电容储能平滑风电场的功率波动[11, 16],但涉及利用超级电容实现故障穿越的研究还不多[13-14]。
笔者对将超级电容应用于永磁同步风电机组来实现故障穿越的控制策略进行了研究,以减小不对称故障所产生的并网负序电流和直流侧2倍工频纹波。
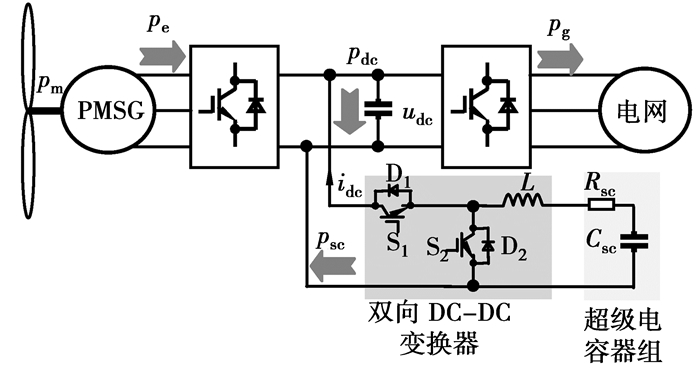
1 含超级电容的直驱风电机组工作原理及其功率分析 1.1 机组结构笔者讨论的含超级电容储能的永磁直驱风电机组结构图如图 1所示。
|
图 1 含超级电容的PMSG拓扑结构 |
图 1中,超级电容器组通过双向DC-DC变换器连接在交直交变流器的直流母线上。对超级电容器组采用不同的控制策略,可以实现不同的目标。如可以控制超级电容器组来实现并网功率的平滑,文献报道的超级电容在风电中的应用一般实现该功能[11, 16],或者实现故障情况下的有功不平衡的吞吐,避免直流母线电压的泵升[13-14]。文中主要研究借助超级电容来实现PMSG机组在不对称故障情况下的故障穿越,除避免直流母线电压的泵升之外,还可同时减小并网负序电流和直流母线电压纹波。
1.2 不对称故障情况下的功率分析图 1中的超级电容储能系统不工作时,即超级电容储能系统输出的功率psc为零。
| $ {p_{{\rm{sc}}}} = {u_{{\rm{dc}}}} \times {i_{{\rm{dc}}}} = 0。$ | (1) |
PMSG的输出功率经交直交换流器并入电网,假设风轮机输出的机械功率为pm,发电机输出的电磁功率为pe,逆变器并入电网的功率为pg。
正常情况下,风轮机的输出机械功率与发电机的输出电磁功率,以及并网功率相等(忽略损耗)。
| $ {P_{\rm{m}}} = {P_{\rm{e}}} = {P_{\rm{g}}}。$ | (2) |
发生短时不对称故障的期间,风轮机输出机械功率为pm可近似为恒定。不对称故障时网侧电压特性一般表现为正序分量幅值下降,同时出现负序电压分量,并网电流中也可能会存在负序分量,不对称故障情况下的并网功率[5]可表示为
| $ \begin{array}{l} \left[{\begin{array}{*{20}{c}} {{P_{{\rm{g}}0}}}\\ {{P_{{\rm{gs}}2}}}\\ {{P_{{\rm{gc2}}}}}\\ {{Q_{{\rm{g0}}}}} \end{array}} \right] = \frac{3}{2}\left[{\begin{array}{*{20}{c}} {{e_{{\rm{dp}}}}}&{{e_{{\rm{qp}}}}}&{{e_{{\rm{dn}}}}}&{{e_{{\rm{qn}}}}}\\ {{e_{{\rm{qn}}}}}&{-{e_{{\rm{dn}}}}}&{-{e_{{\rm{qp}}}}}&{{e_{{\rm{dp}}}}}\\ {{e_{{\rm{dn}}}}}&{{e_{{\rm{qn}}}}}&{{e_{{\rm{dp}}}}}&{{e_{{\rm{qp}}}}}\\ {{e_{qp}}}&{-{e_{{\rm{dp}}}}}&{ - {e_{{\rm{qn}}}}}&{{e_{{\rm{dn}}}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{i_{{\rm{dp}}}}}\\ {{i_{{\rm{qp}}}}}\\ {{i_{{\rm{dn}}}}}\\ {{i_{{\rm{qn}}}}} \end{array}} \right], \end{array} $ | (3) |
式中:Pg0、Qg0为并网平均有功功率及并网平均无功功率;Pgs2为2次有功功率正弦项峰值,Pgc2为2次有功功率余弦项峰值;idp、iqp、idn、iqn分别为并网基波电流的正序、负序电流的d、q分量;edp、eqp、edn、eqn为并网基波电压的正序、负序电压的d、q分量。
由式(3)可得并网有功功率pg的表达式为
| $ \begin{array}{l} {p_g} = {P_{\rm{g0}}} + {P_{\rm{gs2}}}\sin \left( {2\omega t} \right) + {P_{{\rm{gc2}}}}\cos \left( {2\omega t} \right)\\ \;\;\;\;\;\; = {P_{{\rm{g0}}}} + {P_{{\rm{g2}}}}\sin \left( {2\omega t + \theta } \right)。\end{array} $ | (4) |
不对称故障时电网电压跌落,由于网侧换流器的限流,并网功率pg将减小,对应为式(4)中并网有功功率直流分量Pg0下降。同时正负序电压电流还产生式(4)中的有功功率2倍工频波动分量。根据图 1中的功率关系可得
| $ {p_{\rm{e}}}-{p_{\rm{g}}} = \frac{{{\rm{d}}\left( {\frac{1}{2}C{u_{{\rm{dc}}}}^2} \right)}}{{{\rm{d}}t}}。$ | (5) |
由于短时故障期间pm近似恒定,根据式(5)可知电网不对称故障情况下,并网功率pg的直流分量Pg0减小,将导致交直交换流器直流侧电容电压udc泵升,这与对称故障情况相似;同时由于并网功率pg中含有2倍工频波动分量,交直交变流器直流母线上将产生2倍工频电压波动[5],该电压波动将会影响换流器的正常工作。
笔者将借助超级电容来消除不对称故障期间的直流母线电压波动和2倍工频纹波分量,提高永磁同步直驱风电机组的故障穿越能力。
2 超级电容储能系统不对称故障穿越控制策略从1.2节中的分析可以看出,在发生不对称故障时,并网有功中存在波动分量,该波动分量将在直流母线上产生相应的2倍工频电压纹波。当加入超级电容储能系统后,超级电容储能系统输出功率为psc,直流侧电容电压的功率关系由式(5)变为
| $ {p_{\rm{e}}} + {p_{{\rm{sc}}}}-{p_{\rm{g}}} = \frac{{{\rm{d}}\left( {\frac{1}{2}C{u_{{\rm{dc}}}}^2} \right)}}{{{\rm{d}}t}}。$ | (6) |
如果在电网不对称故障情况下,能够控制超级电容储能系统输出有功psc跟踪并网有功pg与发电机输出有功pe的差值Δp,即
| $ {p_{{\rm{sc}}}} = \Delta p = {p_{\rm{g}}}-{p_{\rm{e}}}。$ | (7) |
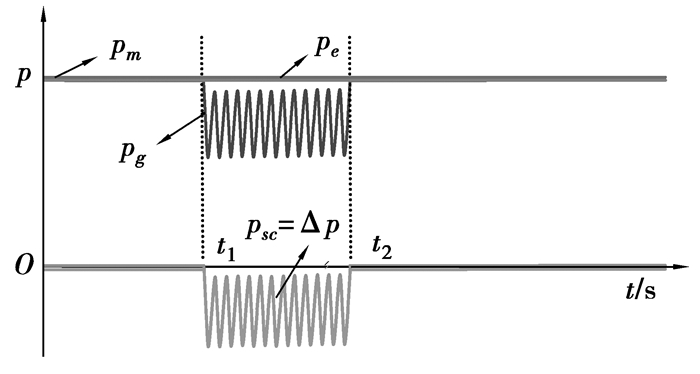
当式(7)满足时,根据式(6)可知,直流侧电容电压的2倍工频纹波能够被消除。文中根据式(7)提出的功率控制思想如图 2所示。
|
图 2 提出的功率控制思想 |
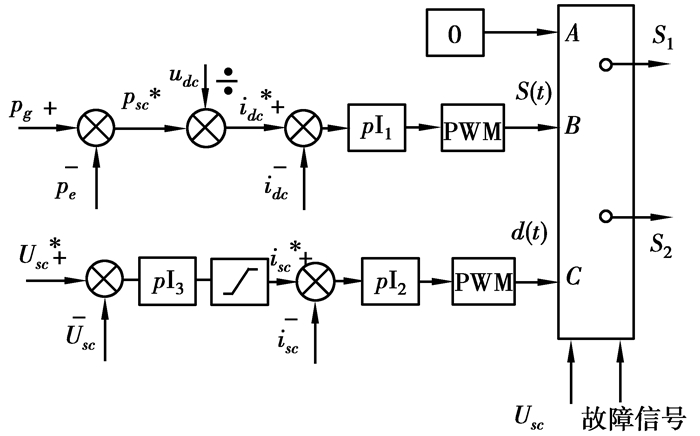
图 1中超级电容器组通过双向DC-DC变换器并联在交直交变换器直流侧,超级电容工作在3种状态:1) 电网正常时的待机状态;2) 电网故障时的故障穿越状态;3) 电网故障消除后的恢复状态。结合超级电容的3种工作状态,图 2中的功率控制思想可以采用图 3所示的控制电路来实现。
|
图 3 双向DC-DC变换器控制框图 |
超级电容的3种工作状态由故障信号和超级电容电压信号共同决定。结合图 3,3种工作状态的切换和控制过程如下:
1) 电网正常时,超级电容工作在状态1,处于待机状态,接受A路信号,S1、S2均输出低电平,双向DC-DC变换器中的两个功率器件均关断。
2) 电网故障期间,超级电容工作在状态2,处于故障穿越状态,接受B路信号。在故障穿越状态,并网功率pg和发电机输出功率pe的差值作为超级电容储能系统输出功率的参考信号psc*,psc*除以直流侧电压udc可得到直流侧输出电流参考信号idc*,通过电流闭环得到双向DC-DC变换器的控制信号d(t)。超级电容处理功率的快速跟踪控制,才能实现直流侧2倍工频纹波的消除,电流环的带宽应较高。
3) 电网故障消除后,超级电容工作在状态3,处于恢复状态,接受C路信号。超级电容因在故障期间吸收能量而致使其电压上升,偏离额定值,在故障消除后,储能系统处于释能工作状态,释放超级电容中储能的能量,为下一次故障穿越提供条件。在故障恢复状态下,采用超级电容的电压电流双环控制来使超级电容电压恢复到额定值。为避免超级电容充放电电流过大,在电压环后加入限幅环节。为了避免释能过快而破坏直流侧电压的稳定,电压环截止频率应较低。当超级电容电压恢复到额定值附近后,第3状态结束,超级电容重新处于待机状态,即第1状态。
在电网发生短时不对称故障瞬时,涡轮机和发电机一般继续保持正常运行,机侧变换器控制策略不变,仍进行最大风能跟踪,而控制网侧变换器实现注入电网电流无负序分量,保证并网电流对称;通过控制超级电容器组吞吐的功率以达到消除直流母线电压的2倍工频纹波的目的, 保证故障期间风电机组仍能正常并网运行。机侧变流器可采用常规的转速外环、电流内环的双闭环控制结构,进行最大风能跟踪的控制[16],如转速环跟踪最佳转速,而电流环采用零d轴电流控制。网侧变流器采用电压外环、电流内环的双闭环控制结构,在电流环的控制中可引入消除并网电流负序分量的控制策略[8]。由于加入文中提出的超级电容不对称故障穿越方法,对原机侧和网侧变流器的控制可以不做修改,文中不再详细介绍。
3 超级电容容量的选取由于超级电容单体额定电压低,需要大量的单体串并联后才能用于风电系统。为了满足对超级电容电压和能量存储的要求,同时尽量减少串并联的超级电容单体数,需要对超级电容容量和构成进行设计。本节将结合风电低电压穿越标准对超级电容的容量选取进行讨论。
由图 2可知,电网不对称故障期间,超级电容处理的功率给定值Δp为直流分量与2倍工频分量之和。Δp的2倍工频分量将导致超级电容电压的2倍工频波动,而超级电容电压的上升量主要取决于Δp的直流分量
| $ E =-\overline {\Delta p} \times t = \frac{{{P_{{\rm{gN}}}} \times \left( {1-U\% } \right)}}{{I\% }} \times t。$ | (8) |
式中:PgN为额定并网功率;U%为电网电压相对于额定值的百分比;I %为电网电流相对于额定值的百分比;t为超级电容的储能时间。
设计由m个单体串联,n组并联构成超级电容组。单体额定耐压为Vrated,设计的超级电容额定端电压为Vsc_rated,则有
| $ m \times {V_{{\rm{rated}}}} = {V_{{\rm{sc\_rated}}}}。$ | (9) |
故障期间,超级电容因储存能量E而致使单体的电压升高,电压升高值为Vup,超级电容单体容值为C,则有
| $ \begin{array}{l} \frac{{nC}}{{2m}} \times \left\{ {{{\left[{m\left( {{V_{{\rm{rated}}}} + {V_{{\rm{up}}}}} \right)} \right]}^2} -{{\left( {m{V_{{\rm{rated}}}}} \right)}^2}} \right\} = E\\ \Rightarrow {V_{{\rm{rated}}}} + {V_{{\rm{up}}}} = \sqrt {\frac{{2E}}{{m \times n \times C}} + {V_{{\rm{rated}}}}^2} 。\end{array} $ | (10) |
由上文可知,故障期间超级电容充放功率为Δp,其单体等效电阻Resr上的压降VResr约为
| $ {V_{{{\mathop{\rm R}\nolimits} _{{\rm{esr}}}}}} = \frac{{\Delta P}}{{m \times {V_{{\rm{rated}}}}}} \times \frac{{{R_{{\rm{esr}}}}}}{n}。$ | (11) |
为保证超级电容储能系统的正常运行,单体电压不能超过单体最大电压值Vmax,则有
| $ \begin{array}{l} {V_{{\rm{rated}}}} + {V_{{\rm{up}}}} + {V_{{{\mathop{\rm R}\nolimits} _{{\rm{esr}}}}}} \le {V_{\max }}\\ \Rightarrow \sqrt {\frac{{2E}}{{m \times n \times C}} + {V_{{\rm{rated}}}}^2} + \frac{{\Delta P}}{{m \times n \times {V_{{\rm{rated}}}}}} \times {R_{{\rm{esr}}}} \le {V_{\max }}。\end{array} $ | (12) |
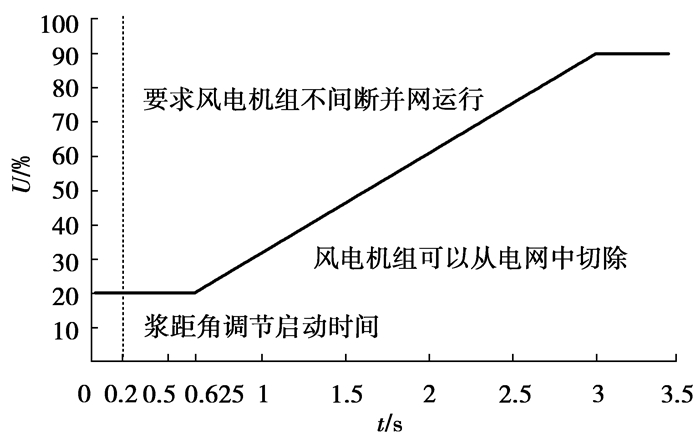
参考中国风电低电压穿越标准[17],图 4为中国故障穿越标准中电网电压跌落程度与风电机组需持续并网运行时间的关系。由图 4可知,风电机组持续并网运行最恶劣的情况是:电网电压有效值跌落至额定值的20%并持续0.625 s。但故障发生0.2 s以后,涡轮机浆距角调节开始响应,进而能根本减少发电机输出有功pe[18],所以超级电容的储能时间t可设定为0.2 s,图 4中黄色区域代表超级电容在故障期间储存的能量。故障期间,并网电流值上升为最大限定值,I%=120%。将额定并网功率PgN=1 MW,U%=20%,I%=120%,t=0.2 s代入式(8),可得E=0.13 MJ。
|
图 4 中国的低电压穿越标准 |
设计的超级电容额定端电压Vsc_rated=400 V,超级电容单体参考MAXWELL公司适合大功率场合1 500 F超级电容[19]。查阅资料得其等效电阻Resr=0.35 mΩ,单体的额定电压Vrated=2.5 V,最大电压Vmax=2.7 V,超级电容在故障期间的储能E=0.13 MW。将以上数据代入式(9)、(12)中可计算得到超级电容器构成为m=160,n=6。对应的超级电容器等效电容值Csc=56.25 F,等效电阻值Rsc=9.3 mΩ。
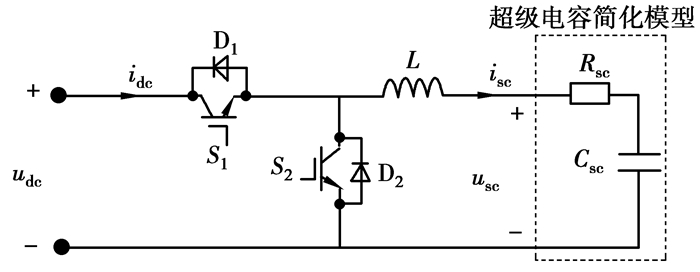
4 超级电容储能系统的数学模型与控制器设计超级电容的物理特性非常复杂,文献[12]采用梯形电路构建了超级电容的分布参数模型,实验显示其特性曲线与实际超级电容特性十分接近。但电压跌落等电网故障持续时间往往很短(≤1 s),因此可以将超级电容简化为只含主导超级电容秒级充电特性的模型[19],如图 5中所示,其中Csc表示超级电容,Rsc表示等效串联电阻。
|
图 5 超级电容储能系统结构 |
超级电容储能系统结构如图 5所示,S1、S2表示开关管(IGBT),D1、D2表示续流二极管,L表示电感,Rsc和Csc构成超级电容的简化模型。图 5所示电路的开关平均模型为
| $ \left\{ \begin{array}{l} L\frac{{d < {i_{{\rm{sc}}}}\left( t \right){ > _{{\rm{Ts}}}}}}{{dt}} = d\left( t \right) < {u_{{\rm{dc}}}}\left( t \right){ > _{{\rm{Ts}}}}-< {u_{{\rm{sc}}}}\left( t \right){ > _{{\rm{Ts}}}}, \\ {C_{{\rm{sc}}}}\frac{{d\left( { < {u_{{\rm{sc}}}}\left( t \right){ > _{{\rm{Ts}}}}-< {i_{{\rm{sc}}}}\left( t \right){ > _{{\rm{Ts}}}}{R_{{\rm{sc}}}}} \right)}}{{dt}} = < {i_{{\rm{sc}}}}\left( t \right){ > _{{\rm{Ts}}}}, \\ < {i_{{\rm{dc}}}}\left( t \right){ > _{{\rm{Ts}}}} = d\left( t \right) < {i_{{\rm{sc}}}}\left( t \right){ > _{{\rm{Ts}}}}, \\ D = \frac{{{U_{{\rm{sc}}}}}}{{{U_{{\rm{dc}}}}}}。\end{array} \right. $ | (13) |
其中d(t)为S1的开关占空比,S1、S2在一个开关周期内互补开通。对式(11)进行小信号扰动分析,可以得到其线性交流小信号模型以用于控制器设计。
| $ \left\{ \begin{array}{l} L\frac{{d\;{i_{{\rm{sc}}}}\hat (t)}}{{dt}} = D\;{{\rm{u}}_{{\rm{dc}}}}\hat (t) + d\hat (t){U_{{\rm{dc}}}}-{u_{{\rm{sc}}}}\hat (t), \\ {C_{{\rm{sc}}}}\frac{{d\;{u_{{\rm{sc}}}}\hat (t)}}{{dt}}-{R_{{\rm{sc}}}}{C_{{\rm{sc}}}}\frac{{d\;{i_{{\rm{sc}}}}\hat (t)}}{{dt}} = {i_{{\rm{sc}}}}\hat (t), \\ {i_{{\rm{dc}}}}\hat (t) = D\;{i_{{\rm{sc}}}}\hat (t) + d\hat (t){I_{{\rm{sc}}}}, \\ D = \frac{{{U_{{\rm{sc}}}}}}{{{U_{{\rm{dc}}}}}}。\end{array} \right. $ | (14) |
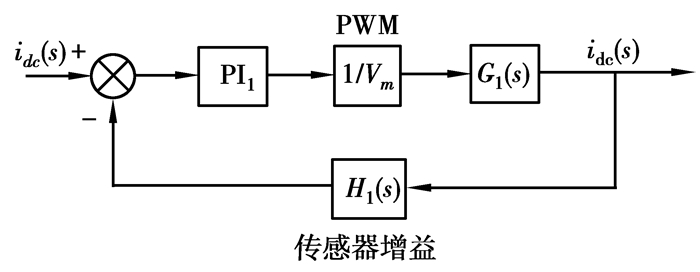
参照图 3中B路信号的设计,构建电流控制环小信号模型,如图 6所示。
|
图 6 电流环小信号模型框图 |
电流环补偿器PI1的设计主要取决于电流传递函数G1(s),如下:
| $ \begin{array}{l} {G_1}\left( s \right) = \frac{{{i_{{\rm{dc}}}}\mathop (\limits^ \wedge s)}}{{d\mathop (\limits^ \wedge s)}}\\ = \frac{{D{U_{{\rm{dc}}}}}}{{sL + {R_{{\rm{sc}}}} + \frac{1}{{s{C_{{\rm{sc}}}}}}}} + {I_{{\rm{sc}}}}。\end{array} $ | (15) |
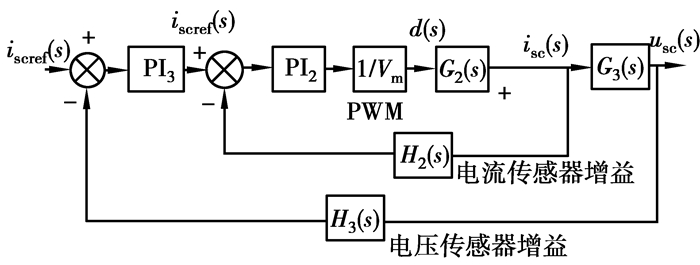
同理,参照2节中C路信号的设计,构建电流内环电压外环的小信号模型,如图 7所示。
|
图 7 电压电流双环小信号模型框图 |
电流传递函数G2(s)和电压传递函数G3(s)如下:
| $ \left\{ \begin{array}{l} {G_2}\left( s \right) = \frac{{{i_{{\rm{sc}}}}\mathop (\limits^ \wedge s)}}{{d\mathop (\limits^ \wedge s)}} = \frac{{{U_{{\rm{dc}}}}}}{{sL + {R_{{\rm{sc}}}} + \frac{1}{{s{C_{{\rm{sc}}}}}}}} = \frac{{s{U_{{\rm{dc}}}}{C_{{\rm{sc}}}}}}{{{s^2}L{C_{{\rm{sc}}}} + s{R_{{\rm{sc}}}}{C_{{\rm{sc}}}} + 1}}, \\ {G_3}\left( s \right) = \frac{{{u_{{\rm{sc}}}}\mathop (\limits^ \wedge s)}}{{{i_{{\rm{sc}}}}\mathop (\limits^ \wedge s)}} = {R_{{\rm{sc}}}} + \frac{1}{{s{C_{{\rm{sc}}}}}} = \frac{{1 + s{R_{{\rm{sc}}}}{C_{{\rm{sc}}}}}}{{s{C_{{\rm{sc}}}}}}。\end{array} \right. $ | (16) |
为满足功率的快速响应性,B、C路信号中的电流环截止频率均设计为1 000 Hz;为避免释能过快而破坏直流侧电压的稳定,C路信号中的电压环截止频率设计为2 Hz。传感器和脉宽调制(PWM)的增益均为1,稳态时,取Udc=1 200 V,Usc=400 V,Isc=0 A,并将L=0.1 mH,Csc=56.25 F,Rsc=9.3 mΩ也代入式(15)、式(16),可计算得图 3中PI调节器的参数。
5 仿真验证电力系统中常见的不对称故障有单相接地短路故障、相间短路故障和两相接地故障。限于篇幅,笔者只给出了单相接地短路故障时的仿真波形,同时给出了文献[13]中没有考虑电网不对称故障时交直交换流器直流侧母线电压波动的仿真对比。在MATLAB中建立了1 MW永磁同步风电机组的系统仿真模型,主要对文中提出的不对称故障情况下的故障穿越控制方法进行了验证,仿真参数如表 1所示。
| 表 1 1 MW PMSG风力发电机组仿真参数 |
笔者主要针对短时的电网不对称故障,更长时间的故障可通过调节风机的浆距角,进而从机械控制的角度消除有功的不平衡。浆距角控制的响应时间通常为0.2 s左右[18],故仿真中设置单相接地故障发生在0.5~0.7 s,持续时间为0.2 s。正常情况下,电网相电压有效值Urms=400 V;发生单相接地故障,正序相电压有效值Urms+=265.58 V,负序电压有效值Urms-=132.79 V,电压不平衡度为50%。参考中国风电并网标准中要求无功调节容量范围为额定运行时功率因数0.97(超前)~0.97(滞后)[17],故仿真中正常时段和故障时段并网无功功率分别控制为0和0.243 MVar,机侧换流器和网侧换流器在故障情况下均按额定电流的1.2倍限幅。
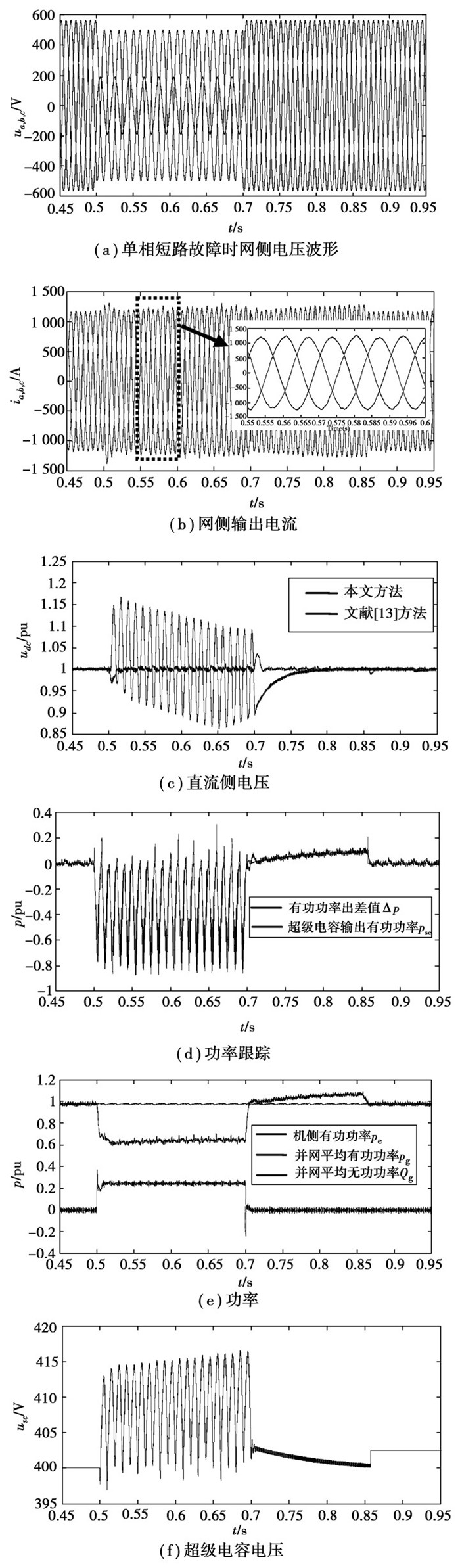
图 8为电网单相接地短路故障时的对应波形。图 8(a)为电网电压通过Y-Y型变压器后逆变器侧的电压波形;图 8(b)为网侧电流波形,采用1.2节中的网侧变流器控制策略后,故障期间电流对称,消除了负序分量,故障消除后,由于超级电容的释能,电网电流高于额定值直至释能结束;从图 8(c)可知,采用文献[13]中的方法,由于没有考虑不对称故障期间直流侧有功不平衡的2倍工频波动,直流侧电压波动值约为稳态值的17%,而采用笔者加入超级电容储能系统的方法直流侧电压波动值仅为稳态值的4%左右,实现了消除电压2倍工频波动的目标;从图 8(d)可看出,采用2节中超级电容储能系统控制策略,超级电容储能系统输出有功psc较好地跟踪了并网有功pg与发电机输出有功pe的差值Δp,以达到消除直流侧电压波动的目的;从图 8(e)可知,故障期间机侧输入有功功率无需改变,而由于需要将超级电容储存的有功释放回电网,故障恢复后存在过载恢复,同时机组在故障期间向电网提供了无功支持,;图 8(f)为超级电容的电压波形,故障期间超级电容因存储有功,电压上升且存在100 Hz的功率脉动,其实质是直流侧的电压2倍工频波动转移到了超级电容上,超级电容进入待工作状态的判定依据是电压恢复到额定值,而由于超级电容器中等效电阻上的电压降影响,超级电容器释能结束进入待工作状态后的稳定电压与额定值存在一定偏差。
|
图 8 仿真结果 |
仿真结果验证了所提出的故障穿越策略实现了并网电流无负序分量,同时减小了直流侧电容电压的2倍工频波动。
6 结语针对采用永磁同步发电机的直驱风力发电系统,分析了发生不对称故障时PMSG系统的功率关系,并提出了利用超级电容储能来实现不对称故障穿越的控制策略,其核心思想是不对称故障情况下超级电容储能系统的输出功率跟踪网侧变换器的输出功率与机侧变换器输入功率之间的差值,在实现了网侧换流器无负序并网电流的基础上,同时减小交直交换流器的直流侧电容电压2倍工频波动。文中提出的控制方法在电网故障时,发电机和交直交变流器的运行均不受影响,仅需对超级电容储能系统进行相应功率控制,仿真结果验证了文中所提方法的有效性。
| [1] |
张治俊, 李辉, 陈宏文, 等.
双馈风电机组总体控制策略及运行性能[J]. 重庆大学学报, 2011, 34(7): 63–68.
ZHANG Zhijun, LI Hui, CHEN Hongwen, et al. Overall control strategy and operational performances of a doubly fed wind turbine generator system[J]. Journal of Chongqing University, 2011, 34(7): 63–68. DOI:10.11835/j.issn.1000-582X.2011.07.011 (in Chinese) |
| [2] |
李辉, 赵斌, 韩力.
风力发电机组暂态模型和稳定性分析方法评价[J]. 重庆大学学报, 2008, 31(5): 481–486.
LI Hui, ZHAO Bin, HAN Li. Assessment of transient models and stability analysis methods for wind power generation units[J]. Journal of Chongqing University, 2008, 31(5): 481–486. DOI:10.11835/j.issn.1000-582X.2008.05.003 (in Chinese) |
| [3] |
胡书举, 李建林, 许洪华.
永磁直驱风电系统低电压运行特性的分析[J]. 电力系统自动化, 2007, 31(17): 73–76.
HU Shuju, LI Jianlin, XU Hongbua. Analysis on the low-voltage-ride-through capability of direct-drive permanent magnetic generator wind turbines[J]. Automation of Electric Power Systems, 2007, 31(17): 73–76. DOI:10.3321/j.issn:1000-1026.2007.17.017 (in Chinese) |
| [4] | 李光琦. 电力系统暂态分析[M]. 北京: 中国电力出版社, 2006. |
| [5] | Chong N, Li R, Bumby J. Unbalanced-grid-fault ride-through control for a wind turbine inverter[C]//Proceedings of 2007 42nd IAS Annual Meeting Conference of the 2007 IEEE Transactions Industry Applications, September 23-27, 207, New Orleans LA. Piscataway:IEEE Press, 2007:154-164. |
| [6] | Abedini A, Nasiri A. PMSG wind turbine performance analysis during short circuit faults[C]//Proceedings of 2007 IEEE Canada Electrical Power Conference, October 25-26, 2007, Montreal, Canada. Piscataway; IEEE Press, 2007:160-165. |
| [7] |
姚骏, 廖勇, 庄凯.
电网故障时永磁直驱风电机组的低电压穿越控制策略[J]. 电力系统自动化, 2009, 33(12): 91–96.
YAO Jun, LIAO Yong, ZHUANG Kai. A low voltage ride-through control strategy of permanent magnet direct-driven wind turbine under grid faults[J]. Automation of Electric Power Systems, 2009, 33(12): 91–96. DOI:10.3321/j.issn:1000-1026.2009.12.019 (in Chinese) |
| [8] | Kim H S, Mok H S, Choe G H, et al. Design of current controller for 3-phase PWM converter with unbalanced input voltage[C]//Proceedings of the 199829th Annual IEEE Power Electronics Specialists Conference, May 17-22, 1998, Fukuoka, Japan. Piscataway:IEEE Press, 1998, 1:503-509. |
| [9] | Alepuz S, Busquets S, Bordonau J, et al. Control of neutral-point-clamped converter in distributed power generation to fulfill low voltage ride-through requirements[C]//Proceedings of 2007 IEEE Power Electronics Specialists Conference, June 17-21, 2007, Orlando, Florida. Piscataway:IEEE Press, 2007:2322-2327. |
| [10] |
肖磊, 黄守道, 黄科元, 等.不对称电网故障下直驱永磁风力发电系统直流母线电压稳定控制的功率控制[J].电工技术学报, 2010, 25(7):123-129. Xiao lei, Huang Shoudao, Huang Keyuan, Ye Sheng.DC Voltage Stability of Directly-Driven Wind Turbine With PM Synchronous Generator During the Asymmetrical Faults[J]. Transactions of China Electrotechnical Society, 2010, 25(7):123-129. |
| [11] | Abbey C, Joos G. Supercapacitor energy storage for wind energy applications[J]. IEEE Transactions on Industry Applications, 2007, 43(3): 769–776. DOI:10.1109/TIA.2007.895768 |
| [12] | Muyeen S M, Takahashi R, Murata T, et al. Integration of an energy capacitor system with a variable-speed wind generator[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 740–749. DOI:10.1109/TEC.2009.2025323 |
| [13] | Hajizadeh A, Golkar M A, Feliachi A. Voltage control and active power management of hybrid fuel-cell/energy-storage power conversion system under unbalanced voltage sag conditions[J]. IEEE Transactions on energy conversion, December, 2010, 25(4): 1195–1208. DOI:10.1109/TEC.2010.2062516 |
| [14] |
张坤, 毛承雄, 陆继明, 等.
基于储能的直驱风力发电系统的功率控制[J]. 电工技术学报, 2011, 26(7): 7–14.
ZHANG Kun, MAO Chengxiong, LU Jiming, et al. Power control strategy of directly drive wind turbine with energy storage system[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 7–14. (in Chinese) |
| [15] |
李霄, 胡长生, 刘昌金, 等.
基于超级电容储能的风电场功率调节系统建模与控制[J]. 电力系统自动化, 2009, 33(9): 86–90.
LI Xiao, HU Changsheng, LIU Changjin, et al. Modelling and controlling of SCES based wind farm power regulation system[J]. Automation of Electric Power Systems, 2009, 33(9): 86–90. DOI:10.7500/AEPS200812038 (in Chinese) |
| [16] | Draou A, Sato Y, Kataoka T. A new state feedback based transient control of PWM AC to DC voltage type converters[J]. IEEE Transactions on Power Electronics, 1995, 10(6): 716–724. DOI:10.1109/63.471291 |
| [17] | Q/GDW392-2009风电场接入电网技术规定[S]. 北京: 国家电网公司, 2009. |
| [18] | Geng H, Yang G. Output power control for variable-speed variable-pitch wind generation systems[J]. IEEE Transactions on Energy Conversion, 2010, 25(2): 494–503. DOI:10.1109/TEC.2009.2034366 |
| [19] | Zubieta L, Richard B. Characterization of double-layer capacitors for power electronics applications[J]. IEEE Transactions on Industry Applications, 2000, 2(1): 199–205. |
 2014, Vol. 37
2014, Vol. 37

