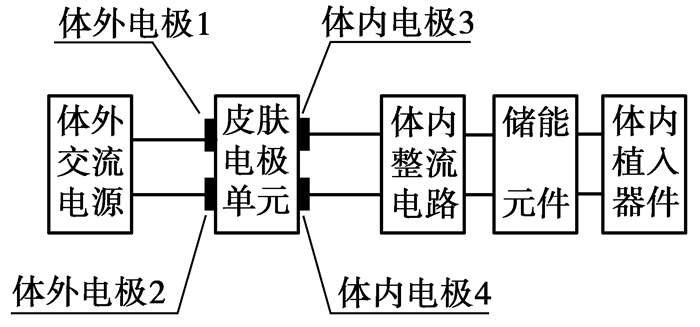
体内植入电子器件具有光明的、广泛的临床应用前景。在目前的植入电子器件应用中,主要以电池技术和磁感应技术供能。电池供能的最大问题是使用寿命受到限制,电能耗尽后需通过外科手术更换电池;而植入电池占植入器件总体积的50%以上,是妨碍微型化的关键因素[1-2]。电磁感应技术虽可将体外电能传递到体内且应用广泛,但会对附近的医疗设备产生射频干扰,而其体内感应线圈限制了植入器件微型化[3]。体导电能量传递技术是植入电子器件能量供给技术的一个重要研究方向。该方式可将丰富的体外电能传递到体内植入器件,是一种有效而稳定的能量供给方案。体导电能量传递系统[4-6]如图 1所示,主要包括体外电能供给电路、皮肤组织及其两侧的电极组成的皮肤电极单元、体内能量转换电路和功能植入器件,是一个复杂的场路耦合系统。由于皮肤电极单元的电极电流是集总电流,文献[2]提出用X型等效二端口网络(图 2)等效替换皮肤电极单元,建立电路模型,研究体导电能量传递系统。因此,能量传递效率[7]等特性与该网络的阻抗参数有关。目前,主要通过实验测量的方法获得该网络阻抗参数,尚无从理论计算方法的角度来获取。
|
图 1 体导电能量传递框图 |

|
图 2 皮肤电极单元的X型等效电路模型 |
笔者研究X型等效二端口网络参数的计算方法,为设计能量传递效率最优的皮肤。
电极单元奠定基础,提出的计算方法如下:
1) 在电极形状和布局一定的条件下,外电极施加正弦电压,通过电磁场原理计算端口电流电压。
2) 通过快速傅里叶变换(FFT)提取端口电流电压的幅值和相位。
3) 在上述激励电压和负载电流确定的条件下,根据X型等效电路(图 2)求取其阻抗参数。
1 场路耦合法计算端口电流电压为了获得体导电中皮肤电极单元端口处的电压、电流参数,建立皮肤电极单元的场路耦合模型。
1.1 场路耦合物理模型体导电“场”“路”耦合物理模型如图 3所示,Ω1、Ω2、Ω3、Ω4为电极区域;Ω5为皮肤组织区域,含有传导电流和位移电流但不含源电流;S1、S2、S3、S4为电极与电路的连接边界;S15、S25、S35、S45为电极与皮肤组织的内部交界面;uin为施加在电极上的交变电压;i1为注入电极的外电流;R0为体内电路部分的等效电阻;uout为其输出电压;i2为该电路的电流。

|
图 3 体导电物理模型 |
体外电压源在电极上施加交变电压,在皮肤组织区域产生交变电场。该电场引起皮肤组织中的带电粒子定向移动,从而在体内、外电极间产生传导电流和位移电流,体内电极接受传递的能量并向体内植入器件供电。
在皮肤电极区域按“场”[8]的观点进行电磁场计算,而在电路上将这些电极与电源、电容、电阻等集总参数相连。这样以电压源为激励,电流作为未知量进行处理符合体导电能量传递的实际情况。
1.2 准静态电场有限元求解体导电能量传递系统的交流电压源频率低于100 kHz时,电磁波的波长大于3 000 m,远大于人体的3维尺寸。因此,把皮肤内的时变电磁场简化为准静态电场[9]。
假设生物组织是各向同性的均匀介质,在皮肤、电极区域内,用磁场强度H和电场强度E表示的场方程和边界条件为
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \times H = \sigma E + \frac{{\partial D}}{{\partial t}},}\\ {\nabla \times E = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \mathit{\Omega} }\\ {\nabla \cdot D = \rho ,} \end{array}} \right. $ | (1) |
| $ \int_S { - n\left( {J + \frac{{\partial D}}{{\partial t}}} \right)} = {I_1},{S_1}、{S_2}; $ | (2) |
| $ \int_S { - n\left( {J + \frac{{\partial D}}{{\partial t}}} \right)} = {I_2},{S_3},{S_4}; $ | (3) |
| $ n \cdot E = 0,{S_5}; $ | (4) |
| $ n \cdot \left( {{E_1} - {E_2}} \right) = 0\;{S_{15}}、{S_{25}}、{S_{35}}、{S_{45}}。$ | (5) |
引入标量电位φ来描述电场强度,即
E=-∇φ,则上述场方程可写成:
| $ \left. { - \frac{{{\xi _0}{\xi _r}{\nabla ^2}\left( {\partial \varphi } \right.}}{{\partial t}}} \right) - \nabla \cdot \left( {\sigma \nabla \varphi } \right) = 0,\mathit{\Omega }; $ | (6) |
| $ \int_s {n \cdot \left( {\sigma \left( {\nabla \varphi } \right) + {\xi _0}{\xi _r}\nabla \frac{{\partial \varphi }}{{\partial t}}} \right){\rm{d}}s} = {I_1},{S_1},{S_2}; $ | (7) |
| $ \int_s {n \cdot \left( {\sigma \left( {\nabla \varphi } \right) + {\xi _0}{\xi _r}\nabla \frac{{\partial \varphi }}{{\partial t}}} \right){\rm{d}}s} = {I_2},{S_3},{S_4}; $ | (8) |
| $ \frac{{\partial \varphi }}{{\partial n}} = 0,{S_5}; $ | (9) |
| $ \frac{{\partial {\varphi _1}}}{{\partial n}} - \frac{{\partial {\varphi _2}}}{{\partial n}} = 0,\;{S_{15}},{S_{25}},{S_{35}},{S_{45}}。$ | (10) |
式中:Ω为整个求解区域;σ为电导率;ξr为相对介电常数。对上述电场方程(6)~(10)采用加权余量法进行伽辽金有限元离散,并整理,式(6)转换成式(11):
| $ \begin{array}{*{20}{c}} {\int_\mathit{\Omega } {\nabla \cdot \left[ {\left( {\sigma \nabla \varphi } \right){N_j}} \right]{\rm{d}}v} - \int_\mathit{\Omega } {\left[ {\left( {\sigma \nabla \varphi } \right)\nabla \cdot {N_j}} \right]{\rm{d}}v} + }\\ {\int_\mathit{\Omega } {\nabla \cdot \left[ {{N_j}{\xi _0}{\xi _r}\nabla \left( {\frac{{\partial \varphi }}{{\partial t}}} \right)} \right]{\rm{d}}v} - }\\ {\int_\mathit{\Omega } {\left[ {{\xi _0}{\xi _r}\nabla \left( {\frac{{\partial \varphi }}{{\partial t}}} \right)\nabla \cdot {N_j}} \right]{\rm{d}}v} = 0\left( {j = 1,2, \cdots ,NP} \right)。} \end{array} $ | (11) |
其中:Nj为权函数;NP为节点总数。
根据边界条件式(7)、式(8)、式(9)和式(10),经过简化,式(11)最后成为
| $ \begin{array}{*{20}{c}} {2\int_{S1} {\frac{{{I_1}}}{{{S_1}}}{N_j} \cdot n{\rm{d}}s} + 2\int_{S3} {\frac{{{I_2}}}{{{S_3}}}{N_j} \cdot n{\rm{d}}s} - \int_\mathit{\Omega } {\left( {\sigma \nabla \varphi } \right)\nabla \cdot {N_j}{\rm{d}}v} - }\\ {\int_\mathit{\Omega } {\left( {{\xi _0}{\xi _r}\nabla \frac{{\partial \varphi }}{{\partial t}}} \right)\nabla \cdot {N_j}{\rm{d}}v} = 0。} \end{array} $ | (12) |
式(12)在整个求解域内空间离散化,可以得到一个时间的一阶微分方程组,将其矩阵形式表示为
| $ \mathit{\boldsymbol{K}}\varphi + \mathit{\boldsymbol{M}}\frac{{\partial \varphi }}{{\partial t}} + \mathit{\boldsymbol{CI}} = 0, $ | (13) |
式中: K为劲度矩阵; M为阻尼矩阵; C、D为耦合劲度矩阵。
1.3 场路耦合电路方程考虑离子型导电的特点和电极极化效应,体导电能量传递系统采用交流激励源,体外场路耦合电路模型如图 4所示。

|
图 4 激励电源电路模型 |
体外电路回路方程为
| $ {u_{{\rm{in}}}} = i{R_1} + {\varphi _1} - {\varphi _2}, $ | (14) |
式中:uin为体外激励电压; i1为回路电流; R1为电源等效内阻; $φ$1、$φ$2分别为电极1、2的电位。写成矩阵即
| $ D\varphi + {R_1}I = {u_{{\rm{in}}}}, $ | (15) |
体内场路耦合模型如图 5所示。

|
图 5 体内电路模型 |
R2为等效串联内阻,体内回路电路方程为
| $ {i_2}{R_2} = {\varphi _3} - {\varphi _4}, $ | (16) |
其中:i2为体内回路电流;$φ$3、$φ$4分别为体内电极3、4的点位。
写成矩阵即
| $ E\varphi = - {R_2}I = 0。$ | (17) |
将式(13)与式(15)、式(17)联立, 可得体导电的场路耦合模型为
| $ \left[ {\begin{array}{*{20}{c}} K&0&C\\ D&{{R_1}}&0\\ E&{ - {R_2}}&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \varphi \\ I\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} M&0&0\\ 0&0&0\\ 0&0&0 \end{array}} \right]\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} \varphi \\ I\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ {{u_{{\rm{in}}}}}\\ 0 \end{array}} \right], $ | (18) |
将其写成标准形式:
| $ \mathit{\boldsymbol{PX}} + \mathit{\boldsymbol{Q}}\frac{{{\rm{d}}\mathit{\boldsymbol{X}}}}{{{\rm{d}}t}} = \mathit{\boldsymbol{f}}, $ | (19) |
其中:
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} K&0&C\\ D&{{R_1}}&0\\ E&{ - {R_2}}&{ - 1} \end{array}} \right],\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} \varphi \\ I\\ 0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} M&0&0\\ 0&0&0\\ 0&0&0 \end{array}} \right],\mathit{\boldsymbol{f}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{u_{{\rm{in}}}}}\\ 0 \end{array}} \right]; $ |
式(19)为时域模型,求解时需进行时间离散。笔者采用中心差分方法进行,其离散格式为
| $ \frac{{Q\left( {{\varphi _{n + 1}} - {\varphi _n}} \right)}}{{\Delta t}} + \frac{{P\left( {{\varphi _{n + 1}} - {\varphi _n}} \right)}}{2} = \frac{{{f_{n + 1}} + {f_n}}}{2}。$ | (20) |
将式(19)代入式(20),整理得:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\frac{M}{{\Delta t}} + \frac{K}{2}}&0&{\frac{C}{2}}\\ {\frac{D}{2}}&{\frac{{{R_1}}}{2}}&0\\ {\frac{E}{2}}&{ - \frac{{{R_2}}}{2}}&{ - \frac{1}{2}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} \varphi \\ I\\ 0 \end{array}} \right]_{n + 1}} = \\ \left[ {\begin{array}{*{20}{c}} {\frac{M}{{\Delta t}} - \frac{K}{2}}&0&{ - \frac{C}{2}}\\ { - \frac{D}{2}}&{ - \frac{{{R_1}}}{2}}&0\\ {\frac{E}{2}}&{\frac{{{R_2}}}{2}}&{\frac{1}{2}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} \varphi \\ I\\ 0 \end{array}} \right]_n} + \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{{{u_{in,n + 1}} + {u_{in,n}}}}{2}}\\ 0 \end{array}} \right]。\end{array} $ | (21) |
式(21)即为体导电能量传递3维瞬态电磁场的场路耦合计算公式。所推导的场路耦合方程虽然增加了几个电流变量,但是方程系数的稀疏对称性的优点却得到了很好的保持;只要知道激励电压条件uin,便可将此时的标量电位$φ$及电极处的瞬变电流i同时求解出来。
2 FFT提取端口电流电压的幅值和相位场路耦合模型已仿真得到皮肤电极单元各端口电压、电流的离散数据,为获取它们的幅值和相位,需对其进行谱分析。考虑到全相位FFT(apFFT)谱分析与有限FFT变换相比具有频谱泄漏少的优点[10-11],且在无噪声的条件下相位无需要校正[12],故选用前者。
现以提取电极电压的幅值和相位为例,apFFT谱分析的具体过程如下:场路耦合模型已得到的电压离散数据为:x(-20), x(-19), …x(0), …, x(20),共41个数据。离散数据来自体导电的单频信号,故可以列出以x(0)为中心的N个N维向量,有:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_0} = {{\left[ {x\left( 0 \right),x\left( 1 \right), \cdots ,x\left( {N - 1} \right)} \right]}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{x}}_1} = {{\left[ {x\left( { - 1} \right),x\left( 0 \right), \cdots ,x\left( {N - 2} \right)} \right]}^{\rm{T}}},}\\ { \cdots \cdots }\\ {{\mathit{\boldsymbol{x}}_{N - 1}} = {{\left[ {x\left( { - N + 1} \right),x\left( { - N + 2} \right), \cdots ,x\left( 0 \right)} \right]}^{\rm{T}}}。} \end{array} $ |
其中,N=21。
将每个向量进行循环移位,把样本点x(0)移到首位,则可得到另外的N个N维向量。对准x(0)相加并取其平均值,则可得到全相位数据向量:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{ap}} = \frac{1}{N}\left[ {Nx\left( 0 \right) + \left( {N - 1} \right)x\left( 1 \right) + x\left( { - N + 1} \right) + \cdots + } \right.}\\ {{{\left. {x\left( {N - 1} \right) + \left( {N - 1} \right)x\left( { - 1} \right)} \right]}^{\rm{T}}}。} \end{array} $ | (22) |
对式(22)进行FFT变换,即得到apFFT谱:
| $ {X_{ap}}\left( k \right) = \frac{A}{{{N^2}}}\frac{{{{\sin }^2}\left[ {{\rm{ \mathsf{ π} }}\left( {\beta - k} \right)} \right]}}{{{{\sin }^2}\left[ {{\rm{ \mathsf{ π} }}\left( {\beta - k} \right)/N} \right]}}{{\rm{e}}^{j{\varphi _0}}},k = 0,1, \cdots ,N - 1。$ |
其幅值为
| $ A = \sum\limits_{k = {k_0} - 2}^{{k_0} + 2} {\left| {{X_{ap}}\left( k \right)} \right|} , $ |
初相位为
| $ {\varphi _0} = {\rm{ang}}\left[ {{X_{ap}}\left( {{k_0}} \right)} \right]。$ |
按照上述方法同样提取各个电极处电流信号的幅值和初相位,由此可进一步得到电流电压的实部和虚部,为接下来用变载法计算X等效电路阻抗参数提供必要的数据。
3 变载法计算X型等效电路阻抗目前可以用来计算X等效模型Z参数的方法有开路法、短路法、最优化方法和参数估计法等。其中,开路法和短路法计算体导电网络参数均会改变皮肤电极域的流线分布结构,因此该方法计算的网络参数不能反映体导电系统正常工作时皮肤电极单元域内的结构特征,导致计算结果不准确。另外,该方法还存在多次改变电路结构和多次提取数据的缺点。参数估计法计算体导电网络参数时数学处理较复杂。最优化方法不仅数学处理复杂,且得到的解不唯一。因为皮肤电极单元参数的计算为一非线性多维无约束最优化问题[13],约束条件不足,该方法往往能求得多个局部最优解,但难以确定全局最优解。
为克服以上方法的不足,笔者引入了一种可以准确计算X等效模型阻抗参数的方法—基于场路耦合的变载法。变载法通过改变负载端负载值,建立方程组计算阻抗参数。该方法既可以避免改变激励源的接线方式,又可以减少方程的个数,使测量数据的数学处理变得简单。
具体来讲,在1、2端串联接入电压源和电阻Rin,在3、4端接入负载R。为简化分析计算,仅考虑激励源内阻和负载均为纯电阻的情况。由此,图 2变为图 7所示。

|
图 7 仿真实验下的变载法 |
当负载R为R1时,电流电压分别记为I10、I20、U10、U20;改变负载为R2时,另记为I11、I21、U11、U21。根据二端口网络知识,得到Z参数方程组(23)和(24)。
| $ \left\{ \begin{array}{l} U_1^0 = {Z_{11}}I_1^0 + {Z_1}2I_2^0,\\ U_2^0 = {Z_2}1I_1^0 + {Z_{22}}I_2^0; \end{array} \right. $ | (23) |
| $ \left\{ \begin{array}{l} U_1^1 = {Z_{11}}I_1^1 + {Z_{12}}I_2^1,\\ U_2^1 = {Z_{21}}I_1^1 + {Z_{22}}I_2^1; \end{array} \right. $ | (24) |
令Zpq=ZpqR+jZpqI(p, q=1, 2),将方程组(23)、(24)按实部虚部分解,可得到含8个未知数8个方程的方程组。即
| $ \begin{array}{l} \left\{ \begin{array}{l} U_{mR}^n = {Z_{m1R}}I_{1R}^n - {Z_{m1I}}I_{1I}^n - {Z_{m2R}}I_{2R}^n + {Z_{m2I}}I_{2I}^n,\\ U_{mI}^n = {Z_{m1R}}I_{1I}^n - {Z_{m1I}}I_{1R}^n - {Z_{m2R}}I_{2I}^n + {Z_{m2I}}I_{2R}^n; \end{array} \right.\\ \;\;\;\;\left( {其中\;m = 1,2;n = 0,1} \right) \end{array} $ |
(其中m=1, 2;n=0, 1)
因为皮肤电极单元对称,所以Z12=Z21。于是方程组成为含6个未知数8个方程的超定线性方程组。代入电流电压的实部和虚部值,解此方程组,可以求出皮肤电极单元等效二端口网络阻抗参数Z11、Z12(Z21)和Z22的实部和虚部。再根据以下关系:
| $ \left\{ \begin{array}{l} {Z_{11}} = {Z_1} + {Z_2} + {Z_5},\\ {Z_{22}} = {Z_3} + {Z_4} + {Z_5},\\ {Z_1} = {Z_2},\\ {Z_3} = {Z_4},\\ {Z_{12}} = {Z_{21}} = {Z_5}。\end{array} \right. $ |
即可求出X等效模型的各个阻抗参数。
4 仿真计算和验证 4.1 仿真计算本仿真实验采用COMSOL Multiphysics3.5a软件搭建实验平台,实现场路耦合的仿真计算。考虑心脏起博器植入胸腔的临床应用,建立皮下植入器件的电极皮肤单元的物理模型,如图 8所示。图中皮肤厚度为6 mm,半径为40 mm,根据意大利应用物理研究院的人体组织的电介特性选择皮肤组织的电导率和相对介电常数,见表 1[14-15];电极材料选用导电率为50 000 s/m的AgCl,厚度为1 mm,内外电极紧贴皮肤组织(其距离为皮肤组织厚度);外激励电压源Uin=20 V,内阻Rin=500 Ω,内电极负载电阻R取R1=1 000 Ω,R2=2 000 Ω。因耦合电路是通过spice语言设置,所以图中模型的电路部分没有显示出来。

|
图 8 COMSOL建立的场路耦合模型 |
| 表 1 皮肤组织电特性 |
为了考察电源频率和电极分布对X等效模型各个阻抗参数的影响,进行了下述3类仿真试验。
图 9为电极半径r=5 mm、电极间距d=10 mm、频率取不同值时得到的X等效模型的阻抗参数。可以看出,当频率增大时,阻抗参数的实部和虚部都减小,但当频率达到4 kHz以后,实部变化较缓慢,而虚部变化也平缓了许多。因此,激励频率应选择大于4 kHz。

|
图 9 阻抗参数与频率的关系 |
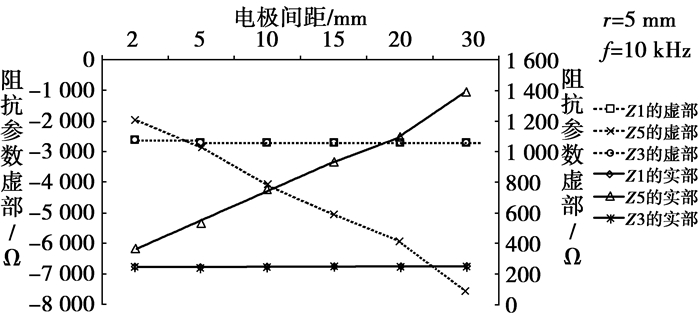
图 10为频率f=10 kHz、电极半径r=5 mm、电极间距取不同值时得到的X等效模型的阻抗参数。当电极间距增大时,Z1和Z3基本保持不变,而Z5随着间距的增大而增大,与电极间距的增大基本上呈线性变化关系。因此,设计电极时,应适当增大电极间距来增大Z5,减小横向电流,提高电流传递效率。
|
图 10 阻抗参数与电极间距的关系 |
图 11为频率f=10 kHz、电极间距d=10 mm、电极半径取不同值时得到的X等效模型的阻抗参数。当半径很小时,阻抗参数很大,随着电极半径的增大,Z1、Z3、Z5都减小;当半径增大到5 mm以后,阻抗参数变化缓慢。因此,宜将电极半径设计在5 mm以上。

|
图 11 阻抗参数与电极半径的关系 |
采用变载法得到的X型等效电路参数搭建电路,比较该电路和场路耦合在相同激励和负载情况下的端口电流电压,可以检验变载法计算的X型等效电路参数的合理性。图 12为PSIM软件搭建的验证电路,图中电极皮肤阻抗单元的参数是电极间距d=10 mm、电极半径r=5 mm、频率f=10 kHz情况下采用变载法的计算值。激励和输入输出电阻与COMSOL设置保持一致:激励电压源Uin=20 V,频率f=10 kHz,输入电阻Rin=500 Ω,输出电阻R=1 000 Ω。计算的端口电流电压见表 2,相对误差小于0.12%,说明变载法计算的X型等效电路参数是合理的。此外,体内电极电流与体外电极电流之比(即电流传递效率)为58%。

|
图 12 PSIM搭建的验证电路 |
| 表 2 COMSOL与PSIM仿真结果比较 |
笔者通过建立场路耦合模型、运用apFFT谱分析和二端口网络的相关理论,采用变载法成功计算出皮肤电极单元X等效电路模型的阻抗参数,并验证了计算结果的正确性。在此基础上研究了这些参数随供能频率、电极间距和电极半径的变化特性。为进一步从电路角度分析和优化体导电能量传递系统的性能提供了基本参数。
| [1] | Deterre M, Boutaud B, Dalmolin R, et al. Energy harvesting system for cardiac implant applications[C]//Proceedings of 2011 Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS (DTIP), May 11-13, 2011, Aix-en-Provence.Piscataway:IEEE Press, 2011:387-391. |
| [2] | Roknsharifi M, Haider M R, Islam S K. A low-power area efficient voltage reference and data generation unit for inductively powered implant system[C]//Proceedings of 2011 IEEE Topical Conference on Biomedical Wireless Technologies, Networks, and Sensing Systems (BioWireleSS), January 16-19, 2011, Phoenix, AZ. Piscataway:IEEE Press, 2011:107-110. |
| [3] | Bradley P D. Wireless medical implant technology-recent advances and future developments[C]//Proceedings of the 2011 European Solid-State Device Research Conference, September 12-16, 2011, Helsinki. Piscataway:IEEE Press, 2011:37-41. |
| [4] | SUN M G, JUSTIN G A, ROCHE P A, et al. Passing data and supplying power to neural implants[J]. IEEE Engineering in Medicine and Biology Magazine, 2006, 25(5): 39–46. DOI:10.1109/MEMB.2006.1705746 |
| [5] | Tang Z D, Sclabassi R J, Su C, et al. Transcutaneous battery recharging by volume conduction and its circuit modeling[C]//Proceedings of 28th Annual International Conference of IEEE Engineering in Medicine and Biology Society, October 30-September 3, 2006, New York, NY. Piscataway:IEEE Press, 2006:644-647. |
| [6] |
唐治德, 赵毅, 张艳, 等.
植入电子器件体导电能量传递模型[J]. 重庆大学学报, 2008, 31(10): 1139–1159.
TANG Zhide, ZHAO Yi, ZHANG Yan, et al. A model for volume conduction energy transfer[J]. Journal of Chongqing University, 2008, 31(10): 1139–1159. DOI:10.11835/j.issn.1000-582X.2008.10.011 (in Chinese) |
| [7] |
唐治德, 吴明鹏, 余小闯, 等.
植入医学器件的电能供给及电磁场仿真[J]. 重庆大学学报, 2010, 33(9): 56–61.
TANG Zhide, WU Mingpeng, YU Xiaochaung, et al. Power supply and electromagnetic simulation of implantable medical devices[J]. Journal of Chongqing University, 2010, 33(9): 56–61. DOI:10.11835/j.issn.1000-582X.2010.09.010 (in Chinese) |
| [8] |
张黎明, 赵燕平, 邓阿丽.
电磁场问题的"场"理论与"路"理论[J]. 现代雷达, 2007, 29(2): 66–79.
ZHANG Liming, ZHAO Yanping, DENG Ali. Electromagnetic fields theory and circuit theory in the analysis of electromagnetic fields problems[J]. Modern Radar, 2007, 29(2): 66–79. (in Chinese) |
| [9] | Chen X L, Benkler S, Chavannes N, et al. Low frequency electromagnetic field exposure study with posable human body model[C]//Proceedings of 2010 IEEE International Symposium on Electromagnetic Compatibility (EMC), July 25-30, 2010, Fort Lauderdale, FL. Piscataway; IEEE Press, 2010:702-705. |
| [10] | Huang X H, Wang Z H, Hou G Q. New method of estimation of phase, amplitude, and frequency based on all phase FFT spectrum analysis[C]//Proceedings of 2007 International Symposium on Intelligent Signal Processing and Communication Systems, November 28-December1, 2007, Xiamen, China. Piscataway:IEEE Press, 2007:284-287. |
| [11] |
李春宇, 张晓林, 张展, 等.
基于D F T的正弦波初相估计算法及误差分析[J]. 北京航空航天大学学报, 2007, 33(5): 580–584.
LI Chunyu, ZHANG Xiaolin, ZHANG Zhan, et al. Phase estimation of sinusoid signal based on DFT and error analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(5): 580–584. (in Chinese) |
| [12] |
王兆华, 黄翔东.
基于全相位谱分析的相位测量原理及其应用[J]. 数据采集与处理, 2009, 24(6): 777–782.
WANG Zhaohua, HUANG Xiangdong. Principle of phase measurement and its application based on all-phase spectral analysis[J]. Journal of data acquisition & processing, 2009, 24(6): 777–782. (in Chinese) |
| [13] | Kiranyaz S, Ince T, Yildirim A, et al. Fractional particle swarm optimization in multidimensional search space[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2010, 40(2): 298–319. DOI:10.1109/TSMCB.2009.2015054 |
| [14] | Institute for applied physics.Dielectric properties of body tissues:Italy[EB/OL]: [2007].http://niremf.ifac.cnr.it/Tissprop. |
| [15] | Federal Communications Commission. Tissue dielectric properties:FCC, Washington, DC[EB/OL], [2008].http://www.fcc.gov/fcc-bin/dielec.sh. |
 2014, Vol. 37
2014, Vol. 37

