电阻抗成像(electrical impedance tomography,EIT)作为一种新型的功能成像技术[1-2],在体表通过电极施加弱的安全电流来测量体表引起的电压,然后将所获得的电压值送回计算机,依照一定的图像重建算法来重建关于被测对象内部的电导率(电阻抗)分布信息的断层图像。EIT具有无创无害、低成本、结构简单和功能成像及动态图像监护的优点[3-4],因而得到国内外众多研究者的广泛关注。
EIT图像重建的本质就是求解逆问题,即已知边界电压,求得目标区域内电导率(电阻抗)的分布,但是其技术困难在于逆问题的不适定性[5]。因此在重建图像算法中通常采用正则化算法来改善其病态性,以得到适定的解[6]。
EIT逆问题中最常用的正则化算法就是Tikhonov正则化算法。此算法的实质是构造特定形式的罚函数来实现对解的阻尼作用,从而达到使解稳定的目的。它的成功应用依赖于正则化参数的合适选取。目前选取正则化参数的方法有Arcangeli准则、偏差原理、岭迹法、广义交叉核实法(generalized cross-validating,GCV)和L曲线法等[7-8]。使用前两种方法来确定正则化参数时,需要先对原始数据的误差水平做出估计。但是关于这些数据的先验性的信息仅便于理论分析,实际中参数的复杂分布导致其难于获取和验证。岭迹法具有直观的优点,但是缺乏严格的理论依据,并且具有主观性和随意性。GCV的缺点在于其函数的变化平缓,甚至难以收敛, 以至于求解的最优值不是全局最优值。L曲线法是目前广泛使用的确定正则化参数的方法,具有函数图像变化明显、定位准确的特点,在控制网评差、GPS快速定位和航天飞行器的精密轨道结算等方面已有应用[9-10],但是在有些情况下L曲线并没有拐点,因此在这种情况下L曲线法失效。
笔者提出了一种新的正则化参数的选取方法,通过极小化正则化算法中的残差范数(residual norm)和解范数(solution norm)的乘积(product of residual norm and solution norm,PRS)来求取正则化参数。理论上该方法较L曲线法更为简单。为验证该方法的有效性,结合二维场域模型,进行了相关的图像重构仿真实验和水槽实验,并与L曲线法进行了对比。结果表明,这种方法更具有优越性。
1 EIT数学模型以二维EIT问题为例[11],EIT的图像重建问题实质上是一个低频电流场的逆问题求解,即已知边界电流和电压,求解内部的电导率分布。通常情况下,被研究区域的电流场被视为准静态场,该电场区域内的电位分布函数φ与电导率分布函数σ满足拉普拉斯方程:
| $ \nabla \cdot \left[ {\sigma \left( {x,y} \right) \cdot \nabla \varphi \left( {x,y} \right)} \right] = 0,\left( {x,y} \right) \in \mathit{\Omega }; $ | (1) |
其边界条件为
| $ \varphi \left( {x,y} \right) = f\left( {x,y} \right),\;\;\left( {x,y} \right) \in \partial \mathit{\Omega }; $ | (2) |
| $ \sigma \left( {x,y} \right)\frac{{\partial \varphi \left( {x,y} \right)}}{{\partial \mathit{\boldsymbol{v}}}} = j\left( {x,y} \right),\;\;\left( {x,y} \right) \in \partial \mathit{\Omega }。$ | (3) |
式中:∂Ω为场域Ω的边界;f为已知边界电位;j为流入场域Ω的电流密度;v为场域边界∂Ω的外法向单位向量。电阻抗成像的正问题是在已知电导率σ分布和边界条件的情况下求取场域内的电位分布φ,而逆问题则是利用已知的边界条件(2)、(3)求解方程(1)中电导率σ的分布。
将场域离散成M个单元,电导率σ0=(σ1, σ2, …, σM-1, σM)T具有M个元素,其中每个元素代表每个单元的电导率。实际电流注入后,所测量的电极上的电压为Vij(i, j=1, 2, …, N),N为电极个数。使用有限元法计算每次电流注入时电极上的电压F(σ0),σ为求得的电导率分布。EIT的线性模型表示为
| $ \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\sigma }}_0}} \right) - \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{J}}\left( {{\mathit{\boldsymbol{\sigma }}_0} - \mathit{\boldsymbol{\sigma }}} \right), $ | (4) |
其中J为Jacobian矩阵。
应用最小二乘法的原理,将式(4)转换为
| $ Z\left( \mathit{\boldsymbol{\sigma }} \right) = \min \left\| {J\left( {{\mathit{\boldsymbol{\sigma }}_0} - \mathit{\boldsymbol{\sigma }}} \right) - \left[ {\mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\sigma }}_0}} \right) - \mathit{\boldsymbol{V}}} \right]} \right\|_2^2。$ | (5) |
电阻抗成像的逆问题就是寻找电导率σ的分布从而使得Ζ(σ)最小。
2 Tikhonov正则化及参数选取 2.1 Tikhonov正则化EIT图像重构的难点是对严重病态的非线性逆问题进行求解,而该问题表现在对条件数很大的Jacobian矩阵求逆。因此对于这样的问题,在求解过程中往往需要利用正则化算法来降低Jacobian矩阵的条件数,改善病态性。
Tikhonov正则化算法是基于最小二乘法的原理,通过在目标函数中引入特定形式的罚函数来对Jacobian矩阵进行惩罚,以求得稳定的解。应用于EIT逆问题的Tikhonov正则化算法的形式[12]为
| $ \begin{array}{*{20}{c}} {E\left( {{\mathit{\boldsymbol{\sigma }}_0} - \mathit{\boldsymbol{\sigma }}} \right) = \min \left\{ {\left\| {J\left( {{\mathit{\boldsymbol{\sigma }}_0} - \mathit{\boldsymbol{\sigma }}} \right) - } \right.} \right.}\\ {\left. {\left. {\left[ {F\left( {{\mathit{\boldsymbol{\sigma }}_0}} \right) - \mathit{\boldsymbol{V}}} \right]} \right\|_2^2 + {\lambda ^2}\left\| {\mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{\sigma }}_0} - \mathit{\boldsymbol{\sigma }}} \right)} \right\|_2^2} \right\}。} \end{array} $ | (6) |
式中:λ>0,为正则化参数,控制着右边残差范数‖J(σ0-σ)-[F(σ0)-V]‖和罚函数‖L(σ0-σ)‖的相对比重;L为正则化矩阵,通常取L=I。
2.2 正则化参数的选取令F(σ0)-V=B,δσ=σ0-σ,则式(6)可以表示为
| $ \mathit{\boldsymbol{E}}\left( {\mathit{\boldsymbol{\delta \sigma }}} \right) = \min \left\{ {\left\| {\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{\delta \sigma }} - \mathit{\boldsymbol{B}}} \right\|_2^2 + {\lambda ^2}\left\| {\mathit{\boldsymbol{\delta \sigma }}} \right\|_2^2} \right\}。$ | (7) |
对式(7)求导可得到解为
| $ \mathit{\boldsymbol{\delta \sigma }} = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}} + {\lambda ^2}\mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{B}}。$ | (8) |
设J∈Rp×q,秩为r,对J进行奇异值分解得:
| $ \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{US}}{\mathit{\boldsymbol{V}}^{\rm{T}}} = \sum\limits_{i = 1}^r {{\mathit{\boldsymbol{u}}_i}{\alpha _i}\mathit{\boldsymbol{v}}_i^{\rm{T}}} , $ | (9) |
式中:U和V分别为S的左右奇异矩阵,且均为正交阵;ui和vi分别为αi在U和V中对应的向量;S为由J的r个奇异值为对角元素组成的矩阵,且α1≥α2 ≥…≥αr-1≥αr>0。则式(8)可写成:
| $ \mathit{\boldsymbol{\delta \sigma }} = \sum\limits_{i = 1}^r {\frac{{\alpha _i^2}}{{\alpha _i^2 + {\lambda ^2}}}\frac{{\mathit{\boldsymbol{u}}_i^{\rm{T}}\mathit{\boldsymbol{B}}}}{{{\alpha _i}}}{\mathit{\boldsymbol{v}}_i}} 。$ | (10) |
称
可见式(7)右边两项均是λ的函数,即
| $ \begin{array}{l} \rho {\left( \lambda \right)^2} = \left\| {\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{\delta \sigma }} - \mathit{\boldsymbol{B}}} \right\|_2^2\\ \;\;\;\;\;\;\;\;\;\; = \sum\limits_{i = 1}^r {\frac{{{\lambda ^2}B_i^2}}{{{{\left( {\alpha _i^2 + {\lambda ^2}} \right)}^2}}}\left\| \gamma \right\|_2^2} , \end{array} $ | (11) |
| $ \eta {\left( \lambda \right)^2} = \left\| {\mathit{\boldsymbol{\delta \sigma }}} \right\|_2^2 = \sum\limits_{i = 1}^r {\frac{{\alpha _i^2B_i^2}}{{{{\left( {\alpha _i^2 + {\lambda ^2}} \right)}^2}}}} 。$ | (12) |
其中
L曲线法是以正则化参数λ为参变量,通过横纵坐标的对比来确定正则化参数。它是基于残差范数‖J·δσ-B‖2和罚函数‖δσ‖2的比值的曲线图。曲线用log-log坐标,具有明显的“L”形状。
Hanke等认为L曲线的关键是定位曲线上曲率最大的那个点,选择其对应的λ为所求的正则化参数。设横坐标和纵坐标分别为
| $ \hat \rho \left( \lambda \right) = \mathit{lg}{\left\| {\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{\delta \sigma }} - \mathit{\boldsymbol{B}}} \right\|_2},\hat \eta \left( \lambda \right) = \lg {\left\| {\mathit{\boldsymbol{\delta \sigma }}} \right\|_2}; $ | (13) |
根据曲率公式:
| $ \kappa = \frac{{\hat \rho '\hat \eta '' - \hat \rho ''\hat \eta '}}{{{{\left[ {{{\left( {\hat \rho '} \right)}^2} + {{\left( {\hat \eta '} \right)}^2}} \right]}^{3/2}}}}, $ | (14) |
式中:
正则化参数的选取应该综合考虑残差范数和解范数对目标函数的贡献,通过减小Jacobian矩阵较小的奇异值对噪声的影响来控制解的光滑程度。在大多数情况下,根据文献[13], 可以通过极小化泛函来实现。
| $ \mathit{\Phi }\left( \lambda \right) = {\left\| {\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{\delta \sigma }} - \mathit{\boldsymbol{B}}} \right\|_2} \cdot {\left\| {\mathit{\boldsymbol{\delta \sigma }}} \right\|_2}。$ | (15) |
Engl[13]等指出,在L曲线的拐点C(
| $ \left[ {\hat \rho '\left( {{\lambda _ * }} \right) + \hat \eta '\left( {{\lambda _ * }} \right)} \right] \cdot \mathit{\Phi }\left( {{\lambda _ * }} \right) = 0; $ | (16) |
即
因此通过对式(15)的求解,可以求得λ的非劣解。对于任何λ,该方法不需像L曲线计算导数和曲率,大大地减少了计算量,节省了运算时间,易于实现。
3 重建结果比较 3.1 模型及设定建立如图 1所示的有限元二维模型,内有1 090个单元、578个节点,采用16电极相邻注入模式。

|
图 1 计算模型 |
仅仅观察重建图像,只能定性地感觉图像的好坏,不能定量评价图像的优劣,因此,依据图像的相关度(correlation degree,CD)[14],残差范数(residual norm,RN)和解的误差范数(error norm,EN)[15]来综合评价不同λ所重建出的图像质量。其中,图像相关度的定义为
| $ {\rm{CD}} = \frac{{\sum\limits_{i = 1}^M {\left( {{\sigma _{{\rm{true}} - i}} - \bar \sigma { - _{{\rm{true}}}}} \right)\left( {{\sigma _{{\rm{rec}} - i}} - {{\bar \sigma }_{{\rm{rec}}}}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^M {{{\left( {{\sigma _{{\rm{true}} - i}} - {{\bar \sigma }_{{\rm{true}}}}} \right)}^2}} \cdot \sum\limits_{i = 1}^M {{{\left( {{\sigma _{{\rm{rec}} - i}} - {{\bar \sigma }_{{\rm{rec}}}}} \right)}^2}} } }}, $ | (17) |
式中:σtrue-i、σrec-i为第i个单元的真实电导率和重建计算出的电导率;σtrue、σrec分别为所有单元的真实电导率与重建计算出的电导率的平均值;M为总单元数。
相关度代表重建的图像与真实图像的相似程度[16]。因此,相关度的值越大,表明重建图像与真实图像越接近,重建的图像质量越好。残差范数和解的误差范数均表示重建图像与真实图像的误差,理论上这两个值越小越好。
3.3 仿真结果为了验证所选择的正则化参数方法的适用性,采用上述模型,利用笔者提出的优化方法和L曲线法进行对比。针对目标区域的电导率、位置、大小以及噪声等不同情况,将仿真实验分为5组。对用式(14)和式(15)所求的正则化参数(分别用λLC和λPRS表示)重建出的图像做比较,并根据上述3个评价指标对图像进行了评价。
3.3.1 改变目标区域位置设置背景区域电导率为3 S/m,目标电导率为1 S/m,目标区域的中心位置分别位于(8, 0),半径约为2,如图 2(a)所示。根据求得的λPRS和λLC重建的图像分别如图 2(b)和(c)所示。
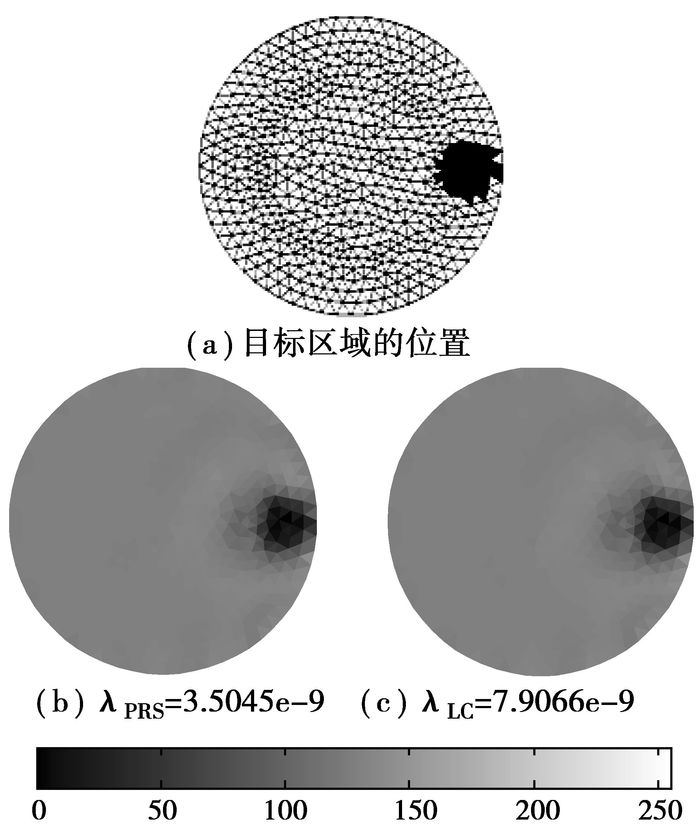
|
图 2 目标区域的中心位于(8, 0) |
需要说明的是,笔者采用的是动态成像,因此灰度条的数值为相对灰度值,并非为绝对电导率值。根据前面给出的3个评价指标来评价它们的质量。另外了还对比两种方法所用的时间,结果见表 1所示。
| 表 1 目标中心位于(8, 0)时的评价结果 |
从上表可以看出,根据该优化方法选取的λ重建的图像与真实图像的相关度较大,同时残差范数和误差范数以及计算时间也较小。因此,利用这种方法能够快速找到相对最优的λ。
改变目标区域的位置至(0, 0),其他参数不变,根据不同的λ重构出的图像和评价结果如图 3和表 2所示。

|
图 3 目标区域的中心位于(0, 0) |
| 表 2 目标中心位于(0, 0)时的评价结果 |
与上文3.3.1中图 2对应,设置背景区域电导率为3 S/m,目标区域电导率为1 S/m,目标区域中心位于(6, 0),半径约为4。根据不同的λ所重建出的图像分别如图 4所示,评价结果如表 3所示。

|
图 4 目标区域半径约为4 |
| 表 3 目标区域半径为4时的评价结果 |
保持目标区域中心不变,仍位于(8, 0),半径约为2,如图 2(a)所示。设置背景区域电导率为3 S/m,目标区域电导率分别为6 S/m。根据不同的λ所重建出的图像如图 5所示,评价指标的计算结果如表 4所示。

|
图 5 目标区域的电导率为6 S/m |
| 表 4 目标区域电导率为6 S/m时的评价结果 |
设置背景区域电导率为3 S/m,目标区域电导率为1 S/m,双目标区域的中心位置分别位于(-8, 0)和(8, 0),半径分别约为2。根据不同的λ所重建出的图像分别如图 6所示,评价结果如表 5所示。
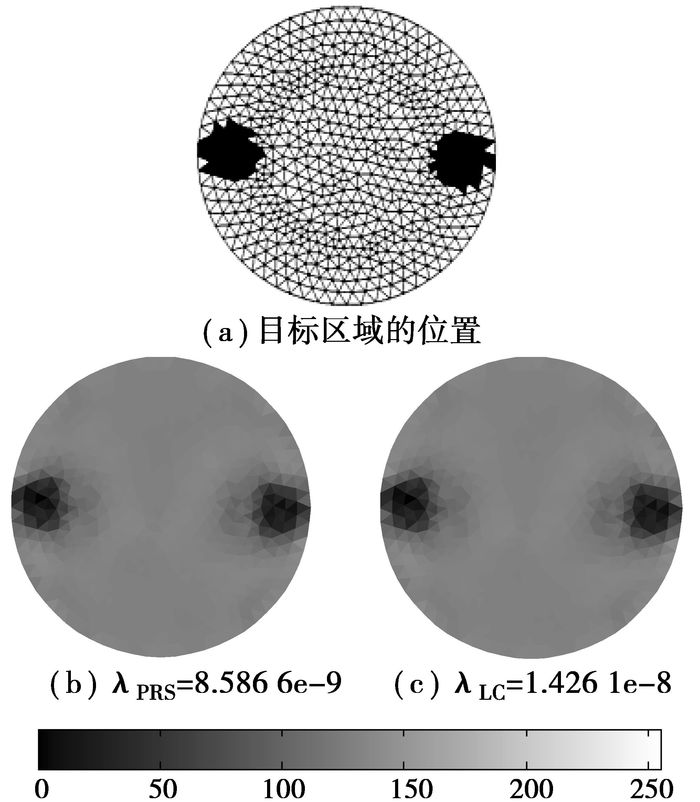
|
图 6 双目标区域 |
| 表 5 双目标时的评价结果 |
为了测试该优化方法的抗噪性,在原始数据的基础上添加不同强度的的高斯白噪声。根据不同的噪声强度,依据该方法计算出相应的λ,再利用所求的λ重建出图像。设置背景区域电导率为3 S/m,目标区域电导率为1 S/m,其中心位置位于(0,0),半径约为2 (如图 3(a)所示)。重建的图像如图 7所示,同样,评价结果如表 6所示。

|
图 7 不同噪声下重建的图像 |
| 表 6 不同噪声下的评价指标的计算结果 |
在实际物理测量中,不可避免会受到多方面因素影响,如硬件系统的测量噪声、工频干扰等,这直接影响最后的重构图像质量。为了验证该方法的有效性,笔者利用其所在团队开发出的二维水槽实时电阻抗成像系统所采集的电压数据,进行了相应的水槽实验,如图 8(a)所示。在水槽中装满水,放入一铝棒,针对图 8(b)两种不同的目标位置,与仿真实验类似,分别利用笔者所改进的方法和L曲线选取的λ进行图像重构,如图 8(c)-(d)所示。

|
图 8 水槽实验模型和重构图像 |
需要说明的是,上图中,深色表示高电导率,浅色表示低电导率。由于铝棒是良导体,其电导率比水要高很多,因此在上图中以黑色表示。
3.5 分析和讨论根据3.3节中前4组仿真实验的重建图像和评价结果,可以看出,当不存在噪声时,根据笔者提出的优化方法求取的λ重建出的图像质量普遍较好,用时较少, 能较好重现目标区域。从而验证了这种正则化参数选取方法的适用性。但需说明,第5组仿真实验中,随着噪声的增加,所重建的图像效果呈恶化趋势。当噪声强度为5%时,图像已经完全失真,背景区域扰动严重,出现有多个虚假的目标,重建图像失败。这是由于Tikhonov正则化算法采取的是2范数的函数为正则化函数,侧重于对适定性问题的解决,而忽略了对逆问题由此产生的有平滑效应,使得重建的图像呈平滑状态,空间分辨率不高,干扰噪声在平滑的过程中被传播和扩散。
在对铝棒的水槽成像实验中,从重构图像中能基本识别出铝棒的位置。横向对比图 8(c)-(d),目标靠近边缘时的图像比目标接近中心区域的图像要好,重构出的目标大小更接近实际目标的大小。纵向对比可以发现采用笔者提出的方法PRS法所重构的图像质量比用L曲线法重构的图像高。但是图像边缘处不均匀,均存在伪影,造成以上现象有以下3点原因:1)硬件测量系统本身的噪声和外界环境中的干扰等因素。2)有限元剖分误差,为了保持全文的一致性,在水槽实验部分采用与仿真实验相同的有限元剖分模型。该有限元模型的剖分密度低,同时利用有限元进行正问题计算时存在模型误差。3)EIT的逆问题是欠定的,成像区域内部大的电导率变化在边界可能产生非常微小的变化,且边界测量值对边缘附近,尤其是电极附近的电导率变化很敏感,而对中心附近电导率变化不敏感,这就导致了目标在中心区域的重构图像质量没有目标在边缘处的图像质量好。
最后,笔者对这种方法作了不适定分析。参数设置如前文3.3.1中相同,λPRS=3.504 5e-9,使用Tikhonov正则化后的Jacobian矩阵的奇异值分解图如图 9所示。
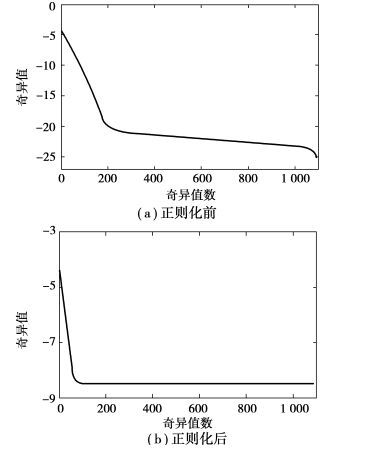
|
图 9 正则化前后Jacobian矩阵的奇异值分解图 |
从上图可以看出,对Jacobian矩阵进行正则化处理后,奇异值仍处于分散的状态,这说明正则化前后Jacobian矩阵的性质没有发生大的变动。经计算,当λPRS=3.504 5e9时,条件数由正则化前的7.672 9e+21减小到2.466 0e+4,说明原Jacobian矩阵的不适定性得到了明显的改善。
4 结语笔者基于Tikhonov正则化算法,结合EIT的模型,利用极小化正则化算法中的残差范数和解范数的乘积的方法来求取正则化参数。并将这种方法引入到EIT图像重构算法中以解决正则化参数优化问题。通过相关的仿真实验和水槽实验,分析比较了根据该方法选取的λ和L曲线法选取的λ分别重建出的图像质量。实验结果表明,该方法具有简单实用和计算时间短的优点。采用所提出的优化方法选取的正则化参数重建的图像质量较好,能够较好地再现目标区域。这为EIT逆问题的病态方程的研究提供了一种实用而有效的参数优化方法,避免了以往选取正则化参数的随意性和主观性,提高了成像质量。
| [1] |
董秀珍.
生物电阻抗成像研究的现状与挑战[J]. 中国生物医学工程学报, 2008, 27(5): 641–643.
DONG Xiuzhen. Recent progress and challenges in the study of bioimpedance imaging[J]. Chinese Journal of Biomedical Engineering, 2008, 27(5): 641–643. (in Chinese) |
| [2] | Holder D S. Electrical impedance tomography of brain function[J]. Brain Topography, 1992, 5(2): 87–93. DOI:10.1007/BF01129035 |
| [3] | Boyle A, Adler A. The impact of electrode area, contact impedance and boundary shape on EIT images[J]. Physiological Measurement, 2011, 32(7): 745–754. DOI:10.1088/0967-3334/32/7/S02 |
| [4] | Abascal J F, Arridge S R, Bayford R H, et al. Comparison of methods for optimal choice of the regularization parameter for linear electrical impedance tomography of brain function[J]. Physiological Measurement, 2008, 29(11): 1319–1334. DOI:10.1088/0967-3334/29/11/007 |
| [5] | 张晓菊. 基于牛顿-拉弗逊正则化算法的开放式电阻抗成像研究[D]. 重庆: 重庆大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10611-2009220288.htm |
| [6] |
黄嵩, 张占龙, 罗辞勇, 等.
电阻抗静态成像中混合正则化算法抗噪性能的仿真研究[J]. 中国生物医学工程学报, 2009, 28(2): 309–313.
HUANG Song, ZHANG Zhanlong, LUO Ciyong, et al. Anti-jamming performance of mixed regularization algorithm in static electrical impedance tomography[J]. Chinese Journal of Biomedical Engineering, 2009, 28(2): 309–313. (in Chinese) |
| [7] | Hansen P C. Analysis of discrete ill-posed problems by means of the L-curve[J]. Society for Industrial and Application Mathematics, 1992, 34(4): 561–580. |
| [8] | Hansen P C, O'leary D P. The use of the L-curve in the regularization of discrete ill-posed problems[J]. SIAM Journal on Science Computing, 1993, 14(6): 1487–1503. DOI:10.1137/0914086 |
| [9] |
吴杰, 李明峰, 余腾.
测量数据处理中病态矩阵和正则化方法[J]. 大地测量与地球动力学, 2010, 30(4): 102–108.
WU Jie, LI Mingfeng, YU Teng. Ill matrix and regularization method in surveying data processing[J]. Journal of Geodesy and Geodynamics, 2010, 30(4): 102–108. (in Chinese) |
| [10] |
李绍新, 许晓安, 徐军发, 等.
基于L曲线法正则参数优化反演光子相关光谱[J]. 华中科技大学学报:自然科学版, 2010, 38(6): 102–106.
LI Shaoxin, XU Xiaoan, XU Jun, et al. Inversion of photon correlation spectroscopy by means of L-curve optimizing regular parameters[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2010, 38(6): 102–106. (in Chinese) |
| [11] |
陈民铀, 张晓菊, 罗辞勇, 等.
开放式电阻抗成像建模及其仿真[J]. 重庆大学学报, 2009, 32(7): 731–735.
CHEN Minyou, ZHANG Xiaoju, LUO Ciyong, et al. Modeling and simulation based on open electrical impedance tomography[J]. Journal of Chongqing University, 2009, 32(7): 731–735. DOI:10.11835/j.issn.1000-582X.2009.07.001 (in Chinese) |
| [12] | Hu L, Wang H X, Zhao B, et al. A hybrid reconstruction algorithm for Electrical impedance tomography[J]. Measurement Science and Technology, 2007, 18(3): 813–818. DOI:10.1088/0957-0233/18/3/033 |
| [13] | Engl H W, Hanke M, Neubauer A. Regularization of Inverse Problems[M].Germany:Springer, 2000. |
| [14] |
周景超, 戴汝为, 肖柏华.
图像质量评价研究综述[J]. 计算机科学, 2008, 35(7): 1–8.
ZHOU Jingchao, DAI Ruwei, XIAO Baihua. Overview of image quality assessment research[J]. Computer Science, 2008, 35(7): 1–8. (in Chinese) |
| [15] | Abascal J F, Arridge S R, Bayford R H, et al. Comparison of methods for optimal choice of the Regularization parameter for linear Electrical impedance tomography of brain function[J]. Physiological Measurement, 2008, 29(11): 1319–1334. DOI:10.1088/0967-3334/29/11/007 |
| [16] |
杨婉, 吴乐华, 范晔.
数字图像客观质量评价方法研究[J]. 通信技术, 2008, 41(7): 244–246.
YANG Wan, WU Lehua, FAN Ye. Study on objective digital image quality assessment methods[J]. Communications Technology, 2008, 41(7): 244–246. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

