磷酸铁锂动力电池具有质量轻、自放电率低、循环寿命长以及能量密度高和功率密度高等特点[1],成为纯电动汽车和混合动力电动汽车动力源的最佳选择之一[2]。而剩余容量(SOC)作为描述电池状态的重要参数,指蓄电池所存储的电量,与电池的开路电压、充放电电流、蓄电池内阻、电解液温度、自放电及电池的循环寿命等参数有关,且呈现较强的非线性,因此如何准确估计SOC是电池管理系统的关键技术之一[3-4]。精确估计SOC能有效防止电池过充过放,充分使用电池,节约电池成本,延长电池的使用寿命,并为电动汽车整车控制提供依据[5],而且精确的SOC还能为驾驶员提供准确的续航里程信息。
在进行SOC检测时,由于动力电池和电池管理系统的工作环境恶劣,数据采集将会受到干扰,进而导致SOC估计不准确。安时积分法和开路电压法是最常用的SOC估计算法,但由于开路电压法需要长时间静置,不能用于在线估计,而安时积分法的初值无法确定且存在传感器误差的累积,只能用于SOC的粗约估计。因此国内外研究人员提出了神经网络、模糊逻辑和卡尔曼滤波等[6-10]SOC估计算法,相对于前两种算法,卡尔曼滤波法具有计算量小,易于实现等特点,但卡尔曼滤波法[11]要求噪声的统计特性已知。而电池管理系统在采集数据过程中噪声统计特性未知,会影响算法的估计性能甚至导致算法不收敛[12]。另外卡尔曼滤波法对模型的依赖程度很高,估计效果受模型精度的影响[13]。
笔者首先根据SOC与开路电压(OCV)的关系来获得初始SOC,然后结合安时积分法采用基于动力电池等效电路模型的自适应卡尔曼滤波法[14]来估计SOC,同时对状态变量、温度等过程噪声和电压、电流采集噪声进行在线预测和修正,提高了SOC估计的精度。最后通过仿真对自适应卡尔曼滤波法和卡尔曼滤波法两种SOC估计算法进行了对比分析和讨论,并通过实验对算法的可行性进行了验证。
1 电池模型的建立相比于其他电池模型,等效电路模型能更直观地表现输入电流与输出电压之间的关系[15],便于电池特性分析和模型参数辨识,而且适用于很多类型的电池。因此,笔者将建立电池等效电路模型进行SOC估计。
等效电路模型的建立要考虑精确性和复杂性两个方面的因素[16]:既要较好地反映电池的动态特性又要便于工程应用。以河南环宇公司的HYP-3.2V/200Ah磷酸铁锂动力电池为研究对象,对电池充放电过程以及充放电结束后的端电压响应分别进行一、二、三阶拟合,直观上等效电路模型的阶数越高,数据拟合程度越好,即越接近实际的实验数据;但模型的阶数越高,模型复杂程度越高,当模型用于电动汽车动力电池SOC在线估计时,计算量越大,计算所用时间越长。而二阶拟合的拟合误差比一阶拟合的拟合误差小得多,与三阶拟合的拟合误差相差不大,因此采用如图 1所示的二阶RC等效电路模型用于SOC估计。
|
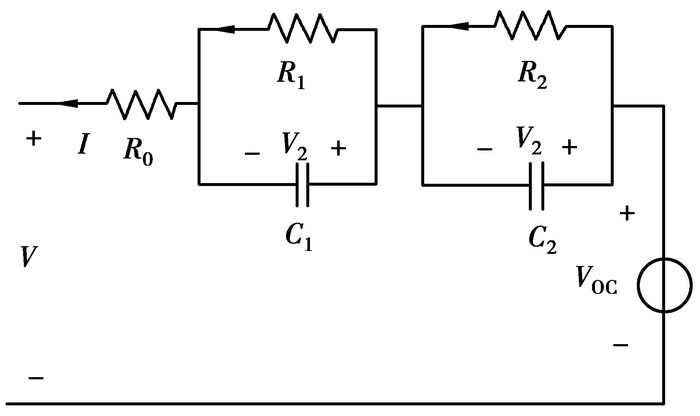
图 1 二阶RC电池模型 |
图 1中,VOC等于电池的开路电压(OCV),与SOC有关;R0表示包括活性物质、集流体、导电极耳以及活性物质/集流体之间的接触电阻;R1和C1分别指扩散层电阻和电容;R2和C2分别为紧密层电阻和电容;I为充放电电流,充电为负,放电为正;V为电池的端电压。
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{V_1}\left( {k + 1} \right)}\\ {{V_2}\left( {k + 1} \right)}\\ {{\rm{SOC}}\left( {k + 1} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_1}\left( {1 - \exp \left( { - \frac{{\Delta t}}{{{R_1}{C_1}}}} \right)} \right)}\\ {{R_2}\left( {1 - \exp \left( { - \frac{{\Delta t}}{{{R_2}{C_2}}}} \right)} \right)}\\ { - \frac{{\eta \Delta t}}{{{C_N}}}} \end{array}} \right]I\left( k \right) + }\\ {\left[ {\begin{array}{*{20}{c}} {\exp \left( { - \frac{{\Delta t}}{{{R_1}{C_1}}}} \right)}&0&0\\ 0&{\exp \left( { - \frac{{\Delta t}}{{{R_2}{C_2}}}} \right)}&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}\left( k \right)}\\ {{V_2}\left( k \right)}\\ {{\rm{SOC}}\left( k \right)} \end{array}} \right],} \end{array} $ | (1) |
| $ V\left( k \right) = \left[ {\begin{array}{*{20}{c}} { - 1}&{ - 1}&{\frac{{{\rm{d}}{V_{OC}}\left( {{\rm{SOC}}} \right)}}{{{\rm{dSOC}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}\left( k \right)}\\ {{V_2}\left( k \right)}\\ {{\rm{SOC}}\left( k \right)} \end{array}} \right] + {R_0}I\left( k \right)。$ | (2) |
对图 1所示的二阶RC电池模型,结合安时积分法[17],以电容C1,C2两端的电压V1,V2以及SOC 3个量为状态变量,充放电电流I为输入变量,电池端电压V为输出变量,可得到式(1)和式(2)所示的离散化的状态空间模型,将在此模型的基础上,采用自适应卡尔曼滤波法估计电池的SOC。
式(1)、(2)中, Δt为采样间隔,取Δt=1s;V1(k)、V2(k)和SOC(k)分别指第k个采样时刻电容C1、C2两端的电压和SOC;V1(k+1)、V2(k+1)和SOC(k+1)分别指第(k+1)个采样时刻电容C1、C2两端的电压和SOC;η为库伦效率;CN为电池的总安时容量;VOC为电池的开路电压,是SOC的函数。
2 电池模型参数的辨识 2.1 电池OCV与SOC关系曲线的测取在后续电池模型阻容参数辨识以及SOC估计中都涉及电池的OCV, 因此求取OCV非常关键。而OCV是SOC的单值函数,故可以通过OCV与SOC关系曲线来得到对应的OCV。笔者采用快速法[18]来获取OCV与SOC的关系曲线,文献[18]已经证明了该方法准确可行。
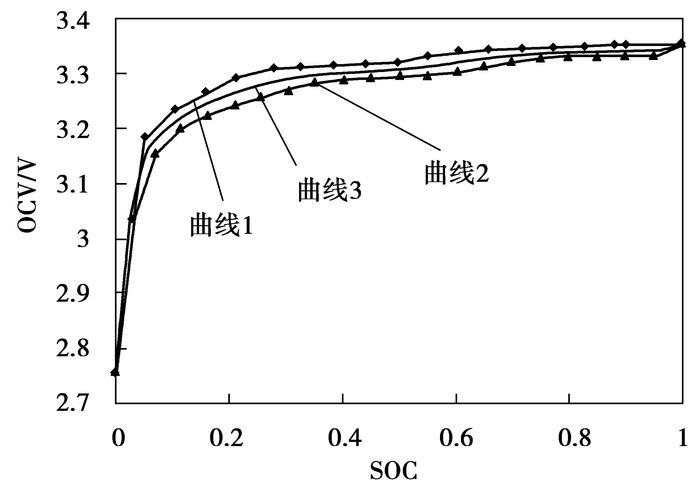
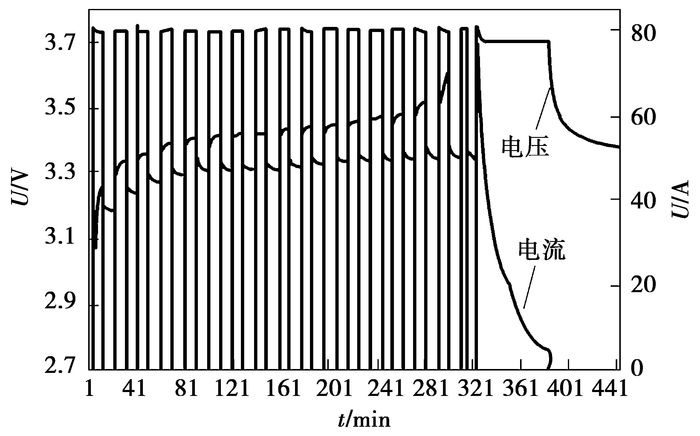
图 3中曲线1是以图 2所示的电流进行分段恒流(80 A)/恒压(3.7 V)充电,恒流阶段每隔5%SOC静置10 min,当端电压上升到3.7 V时静置10 min,此时端电压下降到3.7 V以下,然后再以80 A电流充电到端电压再次上升到3.7 V时进入恒压充电阶段,当充电电流下降到6 A以下充电完成,取静置时间段端电压的极小值点(图 2中每个脉冲电流之后端电压曲线的最小值点和充电完成充分静置后的端电压值)进行曲线拟合得到的;在放电时,取静置时间段电池端电压的极大值点进行曲线拟合得到曲线2;将曲线1和曲线2平均得到曲线3,以曲线3作为OCV与SOC关系曲线。
|
图 3 OCV-SOC曲线 |
|
图 2 充电电压、电流曲线 |
使用指数拟合方法来拟合电池端电压对脉冲电流的响应曲线,进而求出电池模型中的参数。图 1所示的电路模型中放电电流与输出电压的方程可以表示为
| $ \begin{array}{l} V = {V_{OC}} - I{R_0} - I{R_1}\left( {1 - \exp \left( { - \frac{t}{{{R_1}{C_1}}}} \right)} \right) - \\ I{R_2} = \left( {1 - \exp \left( { - \frac{t}{{{R_2}{C_2}}}} \right)} \right)。\end{array} $ | (3) |
所用matlab指数拟合表达式为
| $ V = {c_0} + {c_1}\exp \left( { - {\lambda _1}t} \right) + {c_2}\exp \left( { - {\lambda _2}t} \right), $ | (4) |
式中:c0、c1和c2为常数, 比较式(3)、式(4)可得:
| $ \begin{array}{*{20}{c}} {{R_1} = \frac{{{c_1}}}{I},{R_2} = \frac{{{c_2}}}{I};}\\ {{C_1} = \frac{1}{{{\lambda _1}{R_1}}},{C_2} = \frac{1}{{{\lambda _2}{R_2}}};}\\ {{R_0} = \left( {{V_{{\rm{OC}}}} - {c_0} - {c_1} - {c_2}} \right)/I。} \end{array} $ | (5) |
在求取R0的过程中,由于在平台电压区OCV随SOC的变化很小,会带来较大的误差,因此用下面的方法求取欧姆内阻R0:
对于式(3)有,
|
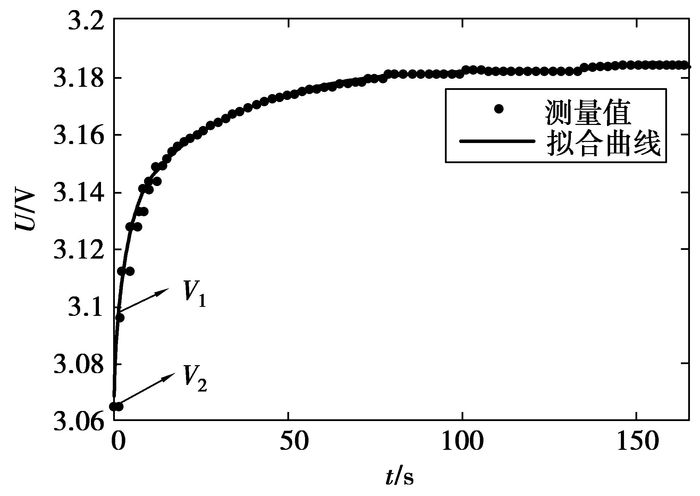
图 4 电流突然为0时的端电压响应曲线 |
| $ {R_0} = \frac{{{V_1} - {V_2}}}{I}。$ | (6) |
式(6)中, V2和V1是电流突然降为0的前后连续2个采样点的电池端电压。
参考《FreedomCAR电池试验手册》,暂不考虑充电情况,采用放电方式,用1C(200A)电流脉冲放电,每隔5%SOC静置1 h,然后利用式(3)~式(6)即可求出不同SOC下模型参数如表 1所示。
| 表 1 电池模型参数表 |
卡尔曼滤波法在估计电池的SOC时,如果假设噪声为高斯白噪声,则效果较好。但实际电池管理系统数据采集时噪声统计特性是未知的,采用自适应卡尔曼滤波法在卡尔曼滤波法的基础上,由测量数据对状态变量进行动态估计,并不断估计和修正噪声的统计特性,进而可以准确地估计电池的SOC。
根据式(1)、式(2),分别用x和y表示状态变量和输出变量,然后作相应的变量替换,即可得到式(7)所示的电池SOC估计模型。
| $ \left\{ \begin{array}{l} {x_{k + 1}} = {A_k}{x_k} + {B_k}{u_k} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{w_k},\\ {y_k} = {C_k}{x_k} + {D_k}{u_k} + {v_k},\\ {v_k} \sim \left( {{r_k},{R_k}} \right),\\ {w_k} \sim \left( {{q_k},{Q_k}} \right); \end{array} \right. $ | (7) |
式中:Γ为3×3干扰矩阵;wk为过程噪声,其均值和协方差分别为qk和Qk;vk为测量噪声,其均值和协方差分别为和rk和Rk。Qk、qk、Rk和rk均未知,通过自适应卡尔曼滤波法进行预测和估计。采用自适应卡尔曼滤波法估计SOC的步骤如式(8)~式(12)所示。
1) 设初始状态估计值x0_est和初始状态误差的协方差P0分别为
| $ \begin{array}{l} {x_{0\_{\rm{est}}}} = E\left[ {{x_0}} \right],\\ {P_0} = E\left[ {\left( {{x_0} - {x_{0\_{\rm{est}}}}} \right){{\left( {{x_0} - {x_{0\_{\rm{est}}}}} \right)}^{\rm{T}}}} \right]。\end{array} $ | (8) |
2) 由k-1(k=1, 2, 3, …)时刻的状态和误差协方差矩阵对k时刻的状态和误差协方差矩阵进行时间更新:
| $ \begin{array}{l} {x_{k\left| {k - 1\_est} \right.}} = {A_k}{x_{k - 1\_est}} + {B_k}{u_k} + \mathit{\Gamma }{\mathit{q}_{k - 1}},\\ {P_{k\left| {k - 1} \right.}} = {A_k}{P_{k - 1}}A_k^{\rm{T}} + \mathit{\Gamma }{Q_{k - 1}}{\mathit{\Gamma }^{\rm{T}}}。\end{array} $ | (9) |
3) 求卡尔曼增益矩阵Lk:
| $ {\mathit{\boldsymbol{L}}_k} = {P_{k\left| {k - 1} \right.}}C_k^{\rm{T}}{\left( {{C_k}{P_{k\left| {k - 1} \right.}}C_k^{\rm{T}} + {R_{k - 1}}} \right)^{ - 1}}。$ | (10) |
4) 用k时刻的输出误差对k时刻的状态和状态协方差矩阵进行时间更新:
| $ \begin{array}{l} {x_{k\_est}} = {x_{k\left| {k - 1\_{\rm{est}}} \right.}} + {L_k}{y_{k\_{\rm{error}}}},\\ {P_k} = \left( {I - {L_k}{C_k}} \right){P_{k\left| {k - 1} \right.}},\\ {y_{k\_{\rm{error}}}} = {y_k} - {C_k}{x_{k\left| {k - 1} \right.}} - {D_k}{u_k} - {r_{k - 1}}。\end{array} $ | (11) |
5) 过程噪声和测量噪声的均值和协方差的更新:
| $ \begin{array}{l} {q_k} = \left( {1 - {d_{k - 1}}} \right){q_{k - 1}} + {d_{k - 1}}G\left( {{x_{k\_est}} - } \right.\\ \;\;\;\;\left. {{A_k}{x_{k - 1\_est}} + {B_k}{u_{k - 1}}} \right),\\ {Q_k} = \left( {1 - {d_{k - 1}}} \right){Q_{k - 1}} + \\ \;\;\;{d_{k - 1}}G\left( {{L_k}{y_{k\_{\rm{error}}}}y_{k\_{\rm{error}}}^{\rm{T}}L_k^{\rm{T}} + {P_k} - {A_k}{P_{k\left| {k - 1} \right.}}A_k^{\rm{T}}} \right){G^{\rm{T}}},\\ {r_k} = \left( {1 - {d_{k - 1}}} \right){r_{k - 1}} + {d_{k - 1}}\left( {{y_k} - {C_k}{x_{k\left| {k - 1\_{\rm{est}}} \right.}} - {D_k}{u_k}} \right),\\ {R_k} = \left( {1 - {d_{k - 1}}} \right){R_{k - 1}} + \\ {d_{k - 1}}\left( {{y_{k\_{\rm{error}}}}y_{k\_{\rm{error}}}^{\rm{T}} - {C_k}{P_{k\left| {k - 1} \right.}}C_k^{\rm{T}}} \right)。\end{array} $ | (12) |
式(8)~式(12)中,Γ=
使用I=20-2.5sin(kΔt)A的变电流放电对上述磷酸铁锂电池进行仿真分析,分别采用卡尔曼滤波算法和自适应卡尔曼滤波算法估计SOC。取采样间隔Δt=1 s,仿真时间为2 400 s,仿真时取系统的初始值和误差协方差矩阵以及测量噪声协方差矩阵分别如下:
| $ {\mathit{\boldsymbol{x}}_0} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {0.99} \end{array}} \right],{\mathit{\boldsymbol{P}}_0} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{Q}}_0} = \left[ {\begin{array}{*{20}{c}} {0.3}&0&0\\ 0&{0.3}&0\\ 0&0&{0.0003} \end{array}} \right]。$ |
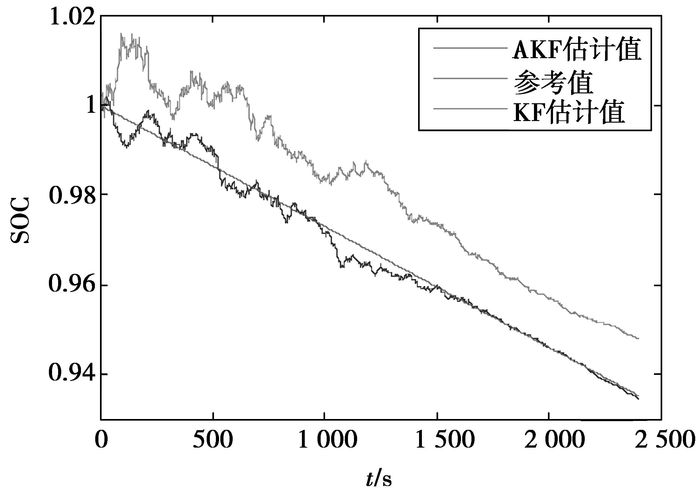
参考表 1所示的参数辨识结果,近似认为电池模型参数在SOC=0.94~1区间内不变,此时取SOC=1时的模型参数进行仿真。仿真结果如图 5和图 6所示,图 5、图 7和图 9中SOC参考值为通过较精确的电流积分计算得到的理论值,“AKF估计值”代表自适应卡尔曼滤波法SOC估计值,“KF估计值”代表卡尔曼滤波法SOC估计值;图 6和图 8中“AKF估计误差”表示自适应卡尔曼滤波法SOC估计误差,“KF估计误差”表示卡尔曼滤波法SOC估计误差。
|
图 5 SOC估计值 |
|
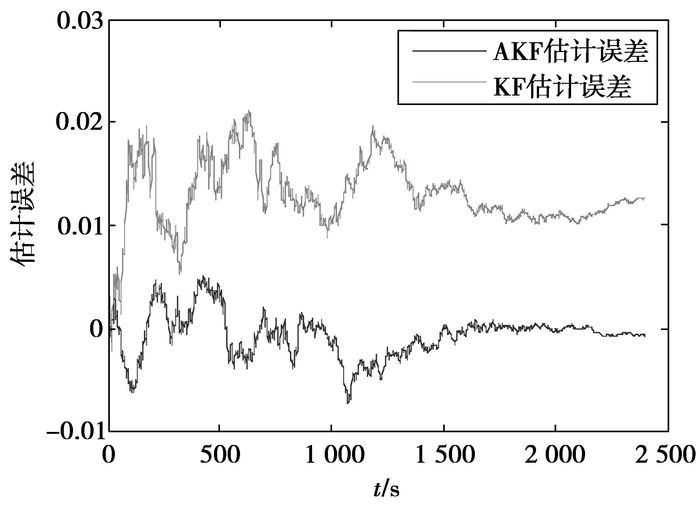
图 6 SOC估计误差 |
|
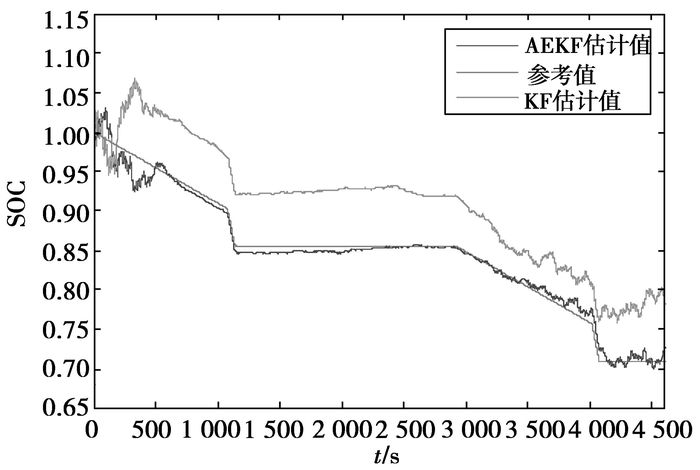
图 7 SOC估计值 |
|
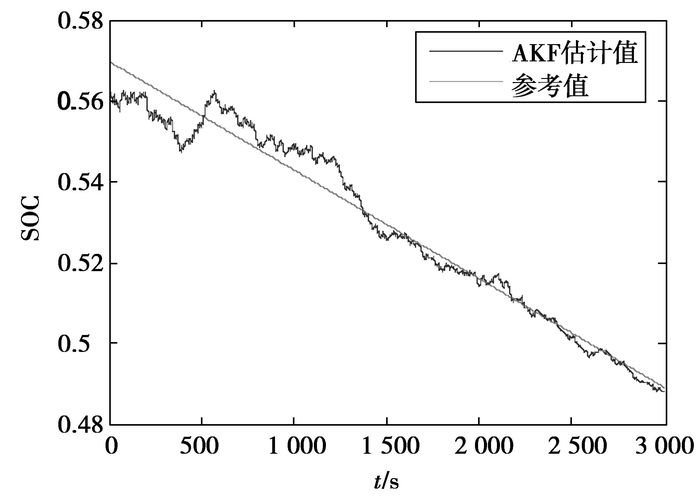
图 9 SOC=0.57时SOC估计值 |
|
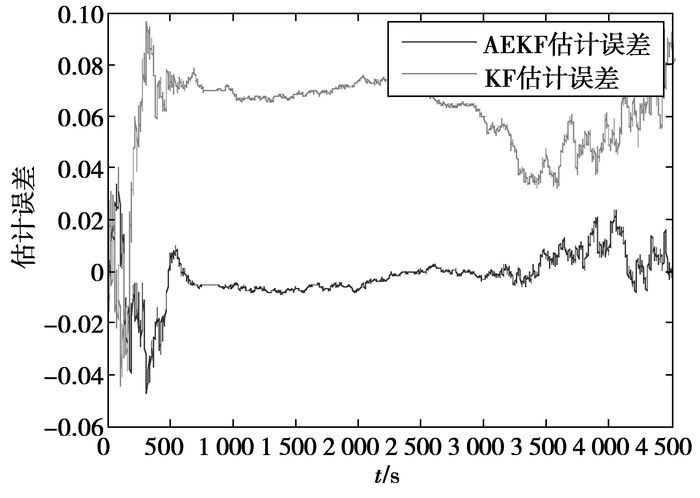
图 8 SOC估计误差 |
从图 5和图 6可以看出,卡尔曼滤波法SOC估计误差为2%左右,而且在仿真阶段的末期,其SOC估计误差趋向于一个稳定的值1%左右。主要是由于卡尔曼滤波法对模型的依赖程度较高,模型微小的误差都可能影响估计效果。笔者近似认为在SOC=0.94~1区间内电池模型参数不变,实际上在这个区间内电池模型参数随SOC的改变存在微小的变化,因此导致SOC估计值与理论值始终存在一定的差值。而自适应卡尔曼滤波法通过实时在线预测和估计系统噪声和输出噪声,进而对SOC预测值进行修正,可以在线修正微小的模型误差带来的SOC估计误差,使SOC估计值收敛于理论值,其SOC估计值在一个很小的范围(±1%)内围绕理论值上下波动,估计误差小于1%,估计精度高于卡尔曼滤波法的SOC估计精度,且自适应卡尔曼滤波法具有较好的鲁棒性。因此自适应卡尔曼滤波法不仅能够有效地降低未知噪声对SOC估计的影响,也减少了算法对模型的依赖程度。
参考《中华人民共和国汽车行业标准QC/T 743—2006,电动汽车用锂离子蓄电池》, 模拟简单放电工况测试,以C/3(66.7A)倍率电流放电18min,再以3C(600A)倍率电流放电1min,静置30min后开始下一个放电工况周期。取两个放电周期进行仿真分析,仿真结果如图 7和图 8所示。由图 7和图 8可以看出,卡尔曼滤波法在整个仿真阶段的SOC估计值与理论值都存在较大的偏差,一方面是由于卡尔曼滤波法在进行SOC估计时假定过程噪声和输出噪声为高斯白噪声,另一方面是由于卡尔曼滤波法对模型的依赖较高;而自适应卡尔曼滤波法的SOC估计值虽然在初始阶段存在较大的误差,为±4%,但经过很短的时间约500s就收敛于理论值,而且能很好地跟随理论值,估计误差明显小于卡尔曼滤波法的估计误差。
按照表 1所示的参数辨识结果对模型参数取值(在SOC=0~4.3%范围内,各参数取SOC=4.3%时的值,以此类推),对电池在SOC=0~1范围内进行上述仿真,得到了类似的结论。
由于磷酸铁锂动力电池在SOC=0.2~0.9区间内,OCV随SOC的变化很小,因此根据开路电压得到的SOC初始值会存在一定误差。因此有必要对初始值进行修正,以减少初值误差对SOC估计的影响。为了验证自适应卡尔曼滤波法对初始误差的修正作用,依照上面的方法,在SOC=0.57时, 取SOC的初值为0.56进行仿真,仿真结果如图 9示。
从图 9以看出虽然初始SOC估计误差较大,但经过较短的时间,约1 300 s,自适应卡尔曼滤波算法SOC估计值收敛到与实际值一致。表明自适应卡尔曼滤波法对初值误差有修正作用,初值越准确收敛速度越快。
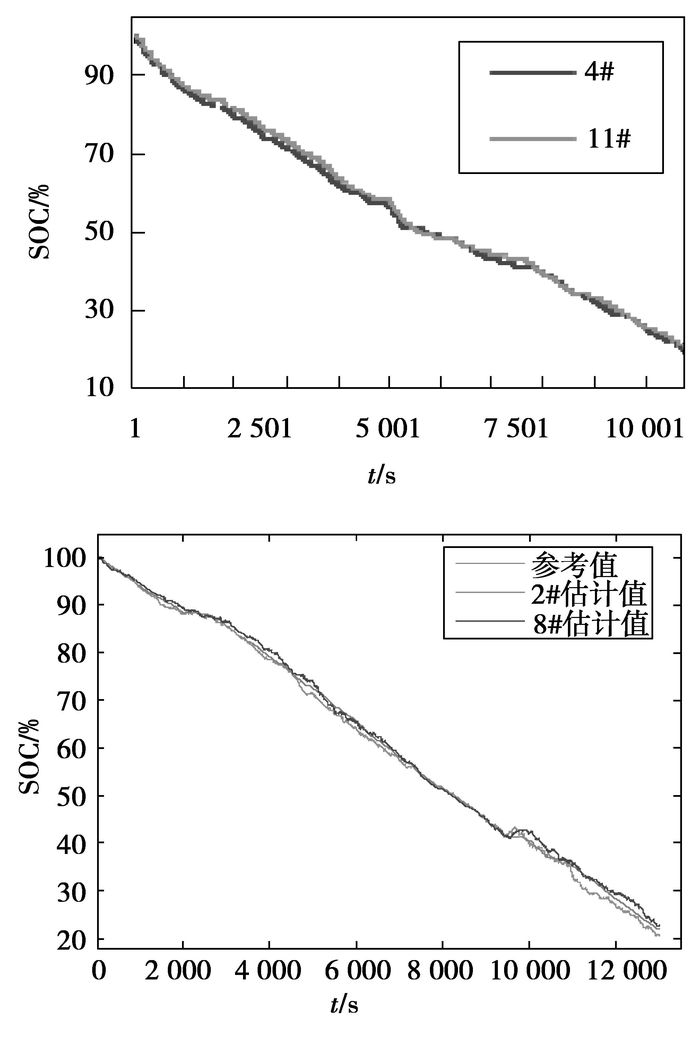
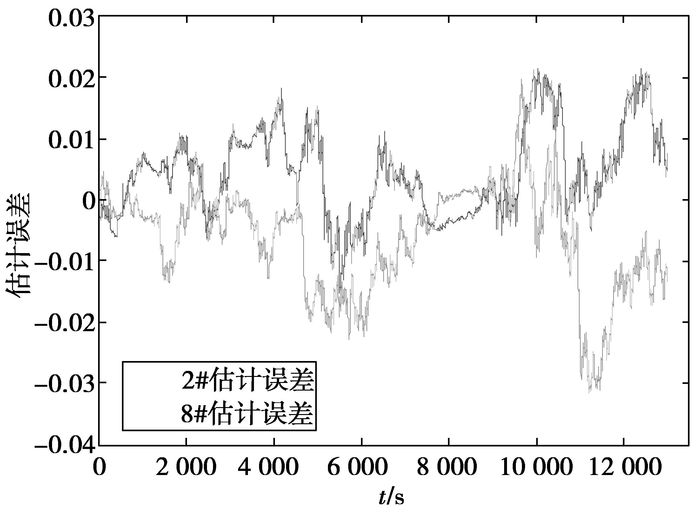
5 实验结果与分析将一组16节200 Ah磷酸铁锂动力电池装车在指定道路上进行实车试验,将SOC估计算法集成到电池管理系统中,并通过上位机监控软件记录各单节电池的SOC,实验结束后,调出2#和8#电池的SOC,得到如图 10所示的SOC估计曲线, 图 10“中参考值”是直接调出采集到的电机母线电流(电池组的电流),通过Ah积分法得到的SOC值。图 11是对应的SOC估计误差。
|
图 10 循环工况实验SOC估计值 |
|
图 11 循环工况实验SOC估计误差 |
从图 10可以看出通过自适应卡尔曼滤波法得到的2#和8#电池的SOC都能围绕参考值在一个很小的范围内上下波动,进一步说明算法得到的SOC比较准确地反映了电动汽车在行驶时SOC的变化情况,验证了算法的可行性。由于电池制造时的差异以及摆放在不同位置的电池散热不同,虽然电池管理系统带有能量均衡管理功能,但由于均衡电流较小,不足以及时消除各单体电池容量上的差异,因此图 10中2#电池和8#电池的SOC曲线不重合,另外由于参考值是通过采集到的电机母线上的电流积分得到的,与实际流过每节单体电池的电流存在微小差异,因而实际误差比仿真误差要大,但实际结果仍满足国家要求的SOC估计精度(±5%)。
6 结语从仿真结果可以看出,自适应卡尔曼滤波法利用测量数据在线估计噪声的均值和方差,然后根据每一步噪声的均值和方差的估计结果不断修正当前的SOC值,而且可以在线修正微小的模型误差对SOC估计精度的影响,可以比较精确地估计SOC,且估计误差明显小于基本卡尔曼滤波法的估计误差。另外,自适应卡尔曼滤波法对SOC初值误差有修正作用,初值越准确收敛速度越快。实验结果进一步验证了自适应卡尔曼滤波法适用于电动汽车用磷酸铁锂动力电池SOC估计。笔者电池模型参数是基于放电实验数据辨识得到的,而充电状态的电池模型参数与放电时不同,因此只验证了算法在放电时的SOC估计精度,对于充电时的情况有待根据充电实验数据辨识的模型参数进一步研究。
| [1] | 桂长清, 等. 实用蓄电池手册[M]. 北京: 机械工业出版社, 2011. |
| [2] | Liu Y H, Luo Y F. Search for an optimal rapid-charging pattern for Li-Ion Batteries using the taguchi approach[J]. Industrial Electronics, IEEE Transactions on Industrial Electronics, 2010, 57(12): 3963–3971. DOI:10.1109/TIE.2009.2036020 |
| [3] | Lee D T, Shiah S J, Lee C M, et al. State-of-Charge estimation for electric scooters by using learning mechanisms[J]. Vehicular Technology IEEEE transactions on Vehicular Technology, 2007, 56(2): 544–556. DOI:10.1109/TVT.2007.891433 |
| [4] |
胡明辉, 秦大同, 舒红, 等.
混合动力汽车电池管理系统SOC的评价[J]. 重庆大学学报:自然科学版, 2003, 26(4): 20–23.
HU Minghui, QIN Datong, SHU Hong, et al. SOC definition of battery management system used in hybrid vehicles[J]. Journal of Chongqing University:Nature Science Edition, 2003, 26(4): 20–23. (in Chinese) |
| [5] |
田光宇, 彭涛, 林成涛, 等.
混合动力电动汽车关键技术[J]. 汽车技术, 2002, 1(1): 8–11.
TIAN Guangyu, PENG Tao, LIN Chengtao, et al. Key technology of hybrid electric vehicle[J]. Automobile Technology, 2002, 1(1): 8–11. (in Chinese) |
| [6] | Malkhandi S. Fuzzy logic-based learning system and estimation of state of charge of lead-acid battery[J]. Engineering Applications of Artificial Intelligence, 2006, 19(5): 479–485. DOI:10.1016/j.engappai.2005.12.005 |
| [7] | Piao C H, Fu W L, Wang J, et al. Estimation of the state of charge of Ni-MH battery pack based on artificial neural network[C]//Proceedings of the 31th International Telecommunications Energy Conference, October 18-22, 2009, Incheon. Piscataway:IEEE Press, 2009:1-4. |
| [8] | 刘浩. 基于EKF的电动汽车用锂离子电池SOC估算方法研究[D]. 北京: 北京交通大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10004-2010119815.htm |
| [9] | Plett G L. Extended Kalman filtering for battery management dystems of Lipb-Based HEV battery packs:part 3. State and parameter estimation[J]. Journal of Power Sources, 2004, 134(2): 277–292. DOI:10.1016/j.jpowsour.2004.02.033 |
| [10] | 杨飞. 磷酸铁力动力电池管理系统的研究[D]. 重庆: 重庆大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10611-2010216521.htm |
| [11] | 付梦印, 邓志红, 张继伟. Kalman滤波理论及其在导航系统中的应用[M]. 北京: 科学出版社, 2003. |
| [12] | Dong T T, Li J, Zhao F Q, et al. Analysis on the influence measurement error on state of charge estimation of LiFePO4 power Battery[C]//Proceedings of 2011 International Conference on Materials for Renewable Energy & Environment, May 20-22, 2011, Shanghai, China. Piscataway:IEEE Press, 2011:644-649. |
| [13] |
阎辉, 肖昌汉, 苏广东.
多模型卡尔曼滤波在地磁场航海测量中的应用[J]. 测绘科学, 2010, 35(1): 41–43.
YAN Hui, XIAO Changhan, SU Guangdong. Application pf multi-model Kalman filtering in surveying marine geomagnetic field[J]. Science of Surveying and Mapping, 2010, 35(1): 41–43. (in Chinese) |
| [14] | He H W, Xiong R, Zhang X W, et al. State-of-charge estimation of lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model[J]. IEEE transactions on Vehicular Technology, 2011, 60(4): 1461–1469. DOI:10.1109/TVT.2011.2132812 |
| [15] |
陈全世, 林成涛.
电动汽车用电池性能模型研究综述[J]. 汽车技术, 2005(3): 1–5.
CHEN Quanshi, LIN Chengtao. Summarization of studies on performance models of batteries for electric vehicle[J]. Automobile Technology, 2005(3): 1–5. (in Chinese) |
| [16] | 胡博. 两类车用动力电池建模与实验研究[D]. 北京: 北京工业大学, 2010. http://d.wanfangdata.com.cn/Thesis/Y1787599 |
| [17] |
夏超英, 张术, 孙宏涛.
基于推广卡尔曼滤波算法的SOC估算策略[J]. 电源技术, 2007, 31(5): 414–417.
XIA Chaoying, ZHANG Shu, SUN Hongtao. A strategy of estimating state of charge based on extended Kalman filter[J]. Chinese Journal of Power Sources, 2007, 31(5): 414–417. (in Chinese) |
| [18] | Suleiman A S, Dennis D. Rapid test and non-linear model characterization of solid-state lithium-ion batteries[J]. Journal of Power Source, 2004, 130(1/2): 266–274. |
 2014, Vol. 37
2014, Vol. 37

