2. 煤矿安全高效开采省部共建教育部重点实验室, 安徽 淮南 232001
2. Key Laboratory of Coal Mine Safety and High Efficiency Mining Cosponsored by Province and MOE, Huainan, Anhui 232001, China
在岩体中开挖巷道后,破坏了岩体初始平衡状态,巷道周围岩体应力发生重新分布,达到二次应力状态。关于巷道围岩应力的分布,国内外学者进行了大量的研究[1-3],1898年Kirsch最早研究了弹性平板中圆孔周围的二维应力分布解,此后,Jaeger和Cook在Kirsch研究的基础上对Kirsch方程进行了详细分析。巷道围岩应力和变形的弹塑性分析方法首先是由R.Fenner提出的,H.Kastner进行了修正。Fenner和Kastner推导出来的公式都是基于理想的弹塑性介质,这与实际岩土类材料的应力应变性状不符。国内学者袁文伯等[4]、马念杰等[5]考虑了岩体应变软化特性给出了巷道围岩应力解,但是没有考虑岩体的扩容特性;姚国圣等[6]针对岩体的应变软化和扩容特性,给出了巷道应力与变形的解析解,然而这些研究皆是在不考虑渗流场影响情况下得到的巷道围岩应力解析解。
地下水是岩体赋存的环境因素之一[7],巷道围岩应力场和位移场必然受到渗流场影响,尤其是深埋于高水头富水环境的巷道,渗流场对巷道围岩应力场和位移场的影响不可忽视。近年来,对于巷道围岩应力场与位移场的研究开始考虑地下水的渗流作用,文献[8]和文献[9]考虑了岩体的应变软化和剪胀特性,推导了圆形水工压力隧洞应力和位移的解析解,却没有考虑围岩的残余强度。文献[10]~[13]分别给出了渗流场影响下圆形隧洞的弹塑性解,但是忽略了岩石的应变软化或扩容特性,所得结果与实际情况存在较大差异。笔者在考虑岩体应变软化、扩容特性和具有水平残余强度的应力应变关系的同时,考虑地下水渗流作用的影响,给出巷道围岩应力、位移与破裂范围的解析公式,具有重要的理论价值和实践意义。
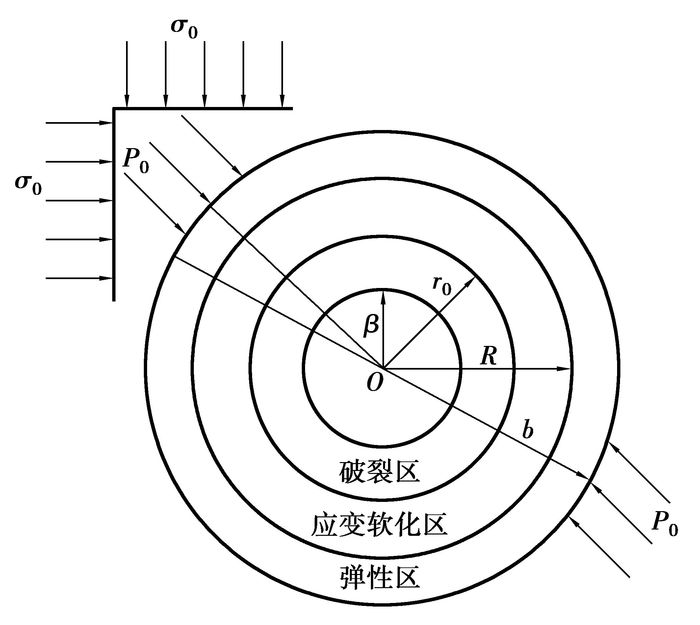
1 渗流场的计算巷道开掘后原岩应力重新分布,巷道围岩内出现应力集中,如果围岩应力小于岩体强度,围岩处于弹性状态,如果围岩应力大于岩体强度,巷道围岩会产生塑性变形,从巷道周边向围岩深处扩展到一定范围内不可避免会产生3个区,即:弹性区、应变软化区、破裂区,简化分析模型如图 1。取地应力为σ0,外水压力为P0,深埋圆形巷道的半径为β,水头为0,计算区域的半径为b,水头为h0。
|
图 1 计算模型 |
假设渗透系数在岩体内各处相同,渗流方向主要以径向渗流为主,岩体是均质、水平、各向同性的,液体是单相、不可压缩且为牛顿液体,渗流过程符合达西定律,故该问题可简化为轴对称恒定渗流问题,其渗流连续微分方程及边界条件[14]为:
| $ \frac{{{{\rm{d}}^2}H}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\;\frac{{{\rm{d}}H}}{{{\rm{d}}r}} = 0。$ | (1) |
由边界条件:H|r=β=0,H|r=b=h0,得孔隙水压力H沿半径方向的分布规律:
| $ H = \frac{{{h_0}}}{{\ln b - \ln \beta }}\ln \frac{r}{\beta }。$ | (2) |
忽略计算区域内岩体的自重,取侧压力系数λ=1.0。由于所考虑的渗流以径向流为主,忽略渗透体积力中的浮力部分,按平面应变轴对称问题考虑,考虑渗透水压力为体积力,结合式(2),则微单元应力平衡微分方程为:
| $ \frac{{{\rm{d}}{\sigma _{\rm{r}}}}}{{{\rm{d}}r}} + \frac{{{\sigma _{\rm{r}}} - {\sigma _\theta }}}{r} - \frac{{{\rm{d}}\left( {\gamma \xi H} \right)}}{{{\rm{d}}r}} = 0, $ | (3) |
| $ G = \frac{{\gamma \xi {h_0}}}{{\ln b - \ln \beta }}。$ | (4) |
式中:σθ,σr分别为切向和径向应力,拉应力为负,压应力为正,ξ为岩石等效孔隙水压力系数,γ为水的重度。
2 巷道围岩中应力和位移解 2.1 巷道围岩弹性区位移和应力巷道围岩应力在弹、塑性区交界上(r=R)满足Mohr-Coulomb准则,即
| $ {\sigma _\theta } = k{\sigma _{\rm{r}}} + {\sigma _{\rm{c}}}, $ | (5) |
式中:
应力边界条件为:σr|r=b=σ0+P0,按平衡微分方程式(3)结合几何条件可得位移、应力计算公式为:
| $ u = {C_1}r + \frac{{{C_2}}}{r} + \frac{F}{2}r\ln r, $ | (6) |
| $ {\sigma _\theta } = E'\left[ {{C_1} + \frac{{\left( {1 - 2\mu } \right){C_2}}}{{{r^2}}} + \frac{F}{2}\ln r + \frac{{\mu F}}{2}} \right], $ | (7) |
| $ \begin{array}{*{20}{c}} {{\sigma _{\rm{r}}} = E'\left[ {{C_1} - \frac{{\left( {1 - 2\mu } \right){C_2}}}{{{r^2}}} + } \right.}\\ {\left. {\frac{F}{2}\ln r + \frac{{\left( {1 - \mu } \right)F}}{2}} \right],} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {{C_1} = \frac{{{\sigma _0} + {P_0}}}{{E'}} + \frac{{1 - 2\mu }}{{{b^2}}}{C_2} - \frac{F}{2}\ln b - }\\ {\frac{{\left( {1 - \mu } \right)F}}{2},} \end{array} $ | (9) |
| $ \begin{array}{*{20}{c}} {{C_2} = \left[ {\frac{{{\sigma _{\rm{c}}} - \left( {1 - k} \right)\left( {{\sigma _0} + {P_0}} \right)}}{{E'}} + \frac{{F\left( {k - 1} \right)}}{2}\ln \frac{R}{b} + } \right.}\\ {\left. {\frac{{\left( {1 - 2\mu } \right)F}}{2}} \right]/\left[ {\left( {1 - 2\mu } \right)\left( {\frac{{1 + k}}{{{R_2}}} + \frac{{1 - k}}{{{b_2}}}} \right)} \right]。} \end{array} $ | (10) |
式中:
大量试验表明,岩体破坏过程具有累进性破坏特性,具体表现为:当应力超过岩体的强度极限时,随变形的增大,岩体强度逐渐衰减,最终达到残余强度值,即岩体存在应变软化现象,同时伴随着体积膨胀。岩体所产生的膨胀可设为图 2所示的线性形式,在塑性区,围岩径向应变和切向应变的增量形式为[15]:

|
图 2 岩体应变软化和扩容特征 |
| $ \varepsilon _{\rm{r}}^{\rm{p}} = \varepsilon _{\rm{r}}^{\rm{e}}\left| {_{r = R}} \right. + \Delta \varepsilon _{\rm{r}}^{\rm{p}}, $ | (11) |
| $ \varepsilon _\theta ^{\rm{p}} = \varepsilon _\theta ^{\rm{e}}\left| {_{r = R}} \right. + \Delta \varepsilon _\theta ^{\rm{p}}; $ | (12) |
且满足:
| $ \Delta \varepsilon _{\rm{r}}^{\rm{p}} = \alpha \Delta \varepsilon _\theta ^{\rm{p}} = 0。$ | (13) |
式中:εrp、εθp分别为径向和切向塑性应变,εre、εθe分别为径向和切向弹性应变,Δεrp、Δεθp分别为巷道围岩中径向塑性应变增量和切向塑性应变增量。α为与岩体扩容特性即破裂膨胀性有关的参数;α>1时,巷道围岩体积膨胀,α=1时,巷道围岩体积不可压缩。
按膨胀条件式(13),并结合式(11)和式(12),则
| $ {\varepsilon _{\rm{r}}} + \alpha {\varepsilon _\theta } = \varepsilon _{\rm{r}}^{\rm{e}}\left| {_{r = R}} \right. + \alpha \varepsilon _\theta ^{\rm{e}}\left| {_{r = R}} \right.。$ | (14) |
在塑性区,围岩发生塑性变形时,其弹性变形很小,因此可以忽略围岩的弹性变形部分,结合式(6)和式(14),并考虑到弹、塑性区交界处位移的连续性,则塑性区位移和切向应变分别为:
| $ \begin{array}{*{20}{c}} {{u^{\rm{p}}} = \left( {{C_1} + \frac{{\alpha - 1}}{{1 + \alpha }}\frac{{{C_2}}}{{{R_2}}} + \frac{F}{2}\ln R + \frac{F}{{2\left( {1 + \alpha } \right)}}} \right)r + }\\ {\frac{{2{C_2}}}{{1 + \alpha }}\frac{{{R^{\alpha - 1}}}}{{{r^\alpha }}} - \frac{F}{{2\left( {1 + \alpha } \right)}}\frac{{{R^{1 + \alpha }}}}{{{r^\alpha }}},} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {\varepsilon _\theta ^{\rm{p}} = {C_1} + \frac{{\left( {\alpha - 1} \right){C_2}}}{{\left( {1 + \alpha } \right){R^2}}} + \frac{F}{2}\ln R + \frac{F}{{2\left( {1 + \alpha } \right)}} + }\\ {\left( {\frac{{2{C_2}}}{{{R^2}}} - \frac{F}{2}} \right)\frac{{{R^{1 + \alpha }}}}{{\left( {1 + \alpha } \right){r^{1 + \alpha }}}}。} \end{array} $ | (16) |
大量实验表明,岩石在破裂过程中内摩擦角几乎不发生变化,其强度衰减主要取决于内聚力的减小,因此,在塑性区,岩体破裂满足:
| $ \sigma _\theta ^{\rm{p}} = k\sigma _{\rm{r}}^{\rm{p}} + \sigma _{\rm{c}}^{\rm{p}}。$ | (17) |
式中:σcp取决于塑性区主应变增量Δεθp和岩体单向抗压强度,即
| $ \sigma _{\rm{c}}^{\rm{p}} = {\sigma _{\rm{c}}} - M\Delta \varepsilon _\theta ^{\rm{p}} = {\sigma _{\rm{c}}} - M\left[ {\varepsilon _\theta ^{\rm{p}} - \varepsilon _\theta ^{\rm{e}}\left| {_{r = R}} \right.} \right]。$ | (18) |
式中,M为岩体应变软化系数。
由式(6)、(16)、(17)和(18)得
| $ \begin{array}{*{20}{c}} {\sigma _\theta ^{\rm{p}} = k\sigma _{\rm{r}}^{\rm{p}} + \sigma _{\rm{c}}^{\rm{p}} - \frac{M}{{1 - \alpha }}}\\ {\left( {\frac{{ - 2{C_2}}}{{{R_2}}} + \frac{F}{2}} \right)\left( {1 - \frac{{{R^{1 + \alpha }}}}{{{r^{1 + \alpha }}}}} \right)。} \end{array} $ | (19) |
把式(19)代入式(3),并利用边界条件σre|r=R=σrp|r=R,得塑性区径向应力和切向应力为
| $\begin{array}{*{20}{c}} {\sigma _{\rm{r}}^{\rm{p}} = \frac{{G + {\sigma _c}}}{{1 - k}} - \frac{M}{{1 + \alpha }}\left( { - \frac{{2{C_2}}}{{{R_2}}} + \frac{F}{2}} \right)}\\ {\left( {\frac{1}{{1 - k}} + \frac{{{R^{1 + \alpha }}}}{{\left( {k + \alpha } \right){r^{1 + \alpha }}}}} \right) + \frac{{{C_3}}}{{{r^{1 - k}}}},} \end{array}$ | (20) |
| $ \begin{array}{*{20}{c}} {\sigma _\theta ^{\rm{p}} = \frac{{kG + {\sigma _c}}}{{1 - k}} - \frac{M}{{1 + \alpha }}\left( {\frac{{ - 2{C_2}}}{{{R_2}}} + \frac{F}{2}} \right)}\\ {\left( {\frac{1}{{1 - k}} - \frac{{\alpha {R^{1 + \alpha }}}}{{\left( {k + \alpha } \right){r^{1 + \alpha }}}}} \right) + \frac{{k{C_3}}}{{{r^{1 - k}}}},} \end{array} $ | (21a) |
式中:
| $ \begin{array}{*{20}{c}} {{C_3} = \left\{ {E'\left[ {{C_1} - \left( {1 - 2\mu } \right)\frac{{{C_2}}}{{{R_2}}} + \frac{F}{2}\ln R + } \right.} \right.}\\ {\left. {\frac{{\left( {1 - \mu } \right)F}}{2}} \right] - \frac{{G + {\sigma _{\rm{c}}}}}{{1 - k}} + \frac{M}{{\left( {1 - k} \right)\left( {k + \alpha } \right)}}}\\ {\left. {\left( { - \frac{{2{C_2}}}{{{R^2}}} + \frac{F}{2}} \right)} \right\}{R^{1 - k}}。} \end{array} $ | (21b) |
取破裂区内岩体的内摩擦角φ也不变,则在破裂区满足:
| $ \sigma _\theta ^{\rm{b}} = k\sigma _{\rm{r}}^{\rm{b}} + \sigma _{\rm{c}}^ * 。$ | (22) |
式中:σθb,σrb分别为破裂区围岩切向应力和径向应力,σc*为岩体单向抗压残余强度。
由式(22)和式(3),并结合边界条件σrb|r=β=0,得破裂区围岩切向和径向应力为
| $ \sigma _{\rm{r}}^{\rm{b}} = \frac{{\sigma _{\rm{c}}^ * + G}}{{1 - k}}\left[ {1 - {{\left( {\frac{\beta }{r}} \right)}^{1 - k}}} \right], $ | (23) |
| $ \sigma _\theta ^{\rm{b}} = \frac{{k\left( {\sigma _{\rm{c}}^ * + G} \right)}}{{1 - k}}\left[ {1 - {{\left( {\frac{\beta }{r}} \right)}^{1 - k}}} \right] + \sigma _{\rm{c}}^ * 。$ | (24) |
在塑性区和破裂区的交界处,即r=r0时,塑性区的应力满足σθp=kσrp+σc*,则塑性区和破裂区的范围由下式确定:
| $ R = {r_0}{\left[ {1 + \frac{{\left( {1 + \alpha } \right)\left( {{\sigma _{\rm{c}}} - \sigma _{\rm{c}}^ * } \right)}}{{M\left( {\frac{{2{C_2}}}{{{R^2}}} - \frac{F}{2}} \right)}}} \right]^{\frac{1}{{1 + \alpha }}}}。$ | (25) |
令
| $ \begin{array}{*{20}{c}} {R = \beta \left[ {1 + 2\left( {1 - \mu } \right)\left( {1 - 2\mu } \right)\left[ {1 + k + \left( {1 - k} \right){{\left( {\frac{R}{b}} \right)}^2}} \right]} \right.}\\ {\left( {1 + \alpha } \right)\left( {{\sigma _{\rm{c}}} - \sigma _{\rm{c}}^ * } \right)/M\left\{ {4\left( {1 - \mu } \right)\left[ {{\sigma _{\rm{c}}} + \left( {k - 1} \right)\left( {{\sigma _0} + {P_0}} \right)} \right] + } \right.}\\ {2G\left( {k - 1} \right)\ln \left( {\frac{R}{b}} \right) + 2\left( {1 - 2\mu } \right)G - }\\ {{{\left. {\left. {G\left( {1 - 2\mu } \right)\left[ {1 + k + \left( {1 - k} \right){{\left( {\frac{R}{b}} \right)}^2}} \right]} \right\}} \right]}^{\frac{1}{{1 + \alpha }}}}。} \end{array} $ | (26) |
由于在塑性区和破裂区交界处径向应力相等,即σrp=σrb,结合式(25),利用下式就可以求得破裂区的半径r0。
| $ \begin{array}{*{20}{c}} {\frac{{G + {\sigma _{\rm{c}}}}}{{1 - k}} + \frac{M}{{1 + \alpha }}\left( {\frac{{2{C_2}}}{{{R^2}}} - \frac{F}{2}} \right)\left[ {\frac{1}{{1 - k}} + \frac{1}{{k + \alpha }}} \right.}\\ {\left. {{{\left( {\frac{R}{{{r_0}}}} \right)}^{1 + \alpha }}} \right] + \frac{{{C_3}}}{{r_0^{1 + k}}} = \frac{{G + \sigma _{\rm{c}}^ * }}{{1 - k}}\left[ {1 - {{\left( {\frac{R}{{{r_0}}}} \right)}^{1 - k}}} \right],} \end{array} $ | (27) |
| $ \begin{array}{*{20}{c}} {{u^b} = {{\left( {\frac{{{r_0}}}{r}} \right)}^2}\frac{{{r_0}}}{{1 + \alpha }}\left[ {\left( {1 + \alpha } \right){C_1} - \left( {1 - \alpha } \right)\frac{{{C_2}}}{{{R_2}}} + \left( {1 + } \right.} \right.}\\ {\left. {\left. \alpha \right)\frac{{F\ln R}}{2} + \frac{F}{2}} \right] + {{\left( {\frac{R}{{{r_0}}}} \right)}^{1 + \alpha }}\frac{1}{{1 + \alpha }}\left( {\frac{{2{C_2}}}{{{R_2}}} - \frac{F}{2}} \right)。} \end{array} $ | (28) |
从式(25)~(28)可见,影响巷道围岩应力、塑性区和破裂范围、位移的因素很多,根据本文的特点,取β=2 m,G=0.1 MPa,应力σ0=10 MPa,σc=20 MPa、σc*=5 MPa,弹性模量E=2 000 MPa,泊松比μ=0.25,内摩擦角φ=40°,岩体有效孔隙水压力系数ξ=1.0。下面只分析承压水压力P0和岩体应变软化系数M和破裂膨胀性α的影响。
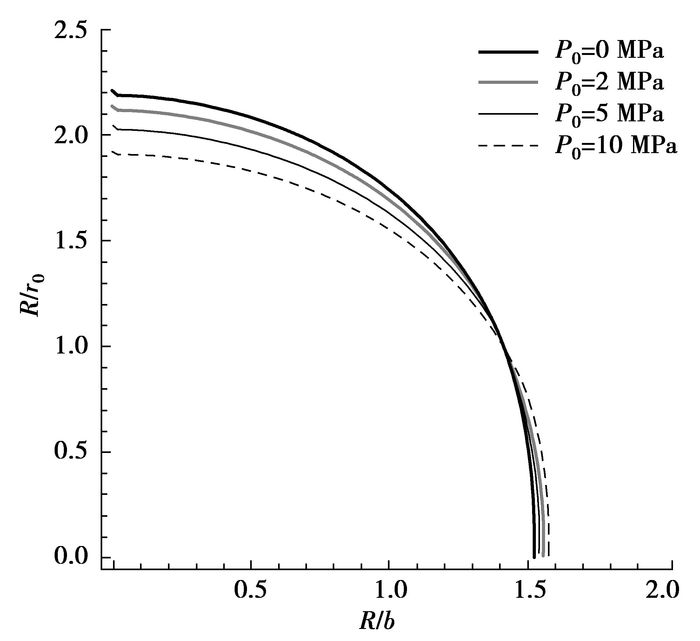
承压水压力P0对围岩塑性区范围和破裂范围的影响如图 3所示。承压水压力P0越大,破裂区和塑性区半径也越大。在其他条件一定时,随着塑性区半径的增大,塑性区和破裂区半径的比值R/r0却越小,说明承压水压力P0对破裂区范围的影响要比对塑性区范围的影响更加明显。
|
图 3 P0与围岩破裂范围关系 |
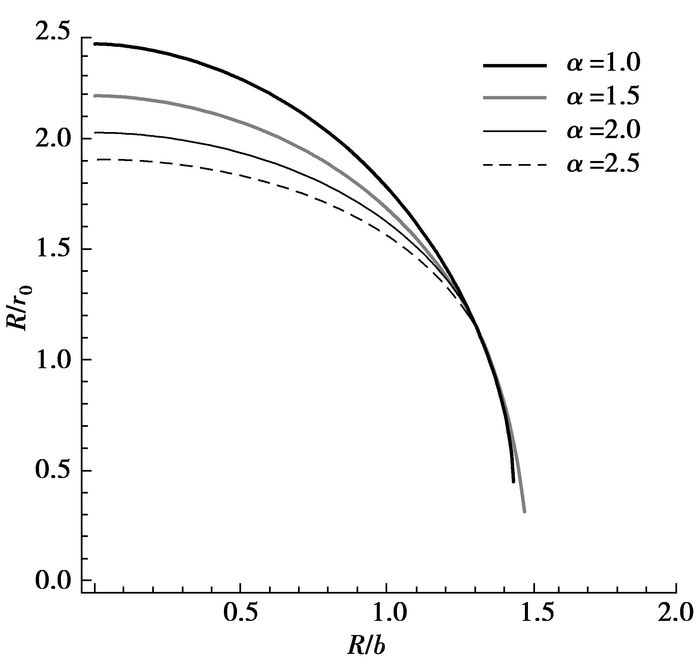
岩体的扩容即破裂膨胀性α对巷道围岩塑性区和破裂范围的影响如图 4所示,图 4表明,岩体的破裂膨胀性对巷道围岩塑性区范围的影响不大,对围岩破裂范围的影响明显,从式(15)和式(28)易知,它对巷道围岩位移的影响也比较明显。在其他条件一定时,随着岩体的膨胀性α的增大,塑性区和破裂区半径的比值R/r0显著减小,因此,进行巷道支护设计时,必须充分考虑岩体的破裂膨胀性对巷道围岩稳定性的影响。
|
图 4 α与围岩破裂范围关系 |
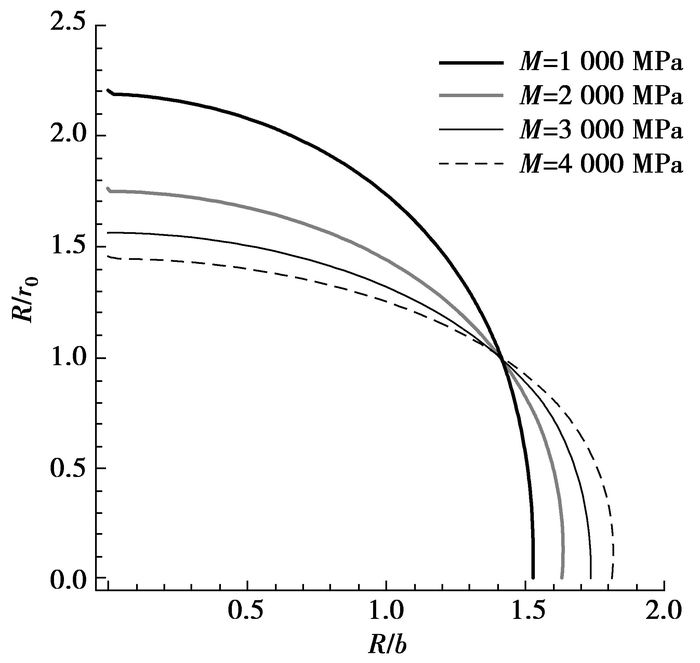
应变软化系数M对围岩塑性区范围和破裂范围的影响显著,如图 5所示。应变软化系数M越大,破裂区和塑性区半径也越大,但R<1.5b时,比值R/r0却越小,也就是说巷道围岩破裂区扩展的速度比巷道围岩塑性区扩展的速度显著得多,当R>1.5b时,随着应变软化系数M的增大,塑性区和破裂区半径的比值R/r0增大,此时巷道围岩破裂区扩展的速度相对巷道围岩塑性区扩展的速度变缓。同时,由式(15)和(28)易知,在渗流作用下,应变软化对巷道围岩位移的影响要比不考虑渗流作用下的巷道围岩位移的影响明显得多。因此,当巷道在渗流作用下时,通过降低应变软化程度,对巷道矿压控制更加有利。
|
图 5 M与围岩破裂范围关系 |
1) 在考虑渗流体积力,岩体应变软化、扩容特性和残余强度的基础上,推导了承压水作用下巷道围岩弹性区、塑性区和破裂区的应力和位移解析解,对于巷道的支护都具有重要的意义。
2) 渗流场对塑性区范围和破裂区范围的影响,随内外水头差的增大而增大,尤其是R<1.5b时对破裂区范围的影响程度要比对塑性区范围的影响更加明显,同时,考虑渗流场影响比不考虑渗流场影响时,塑性区范围和破裂区范围都要大。
3) 在渗流场的影响下,考虑岩体应变软化和膨胀性时,巷道围岩塑性区和破裂区的范围增大,且岩体应变软化对巷道围岩塑性区和破裂区的范围影响同样显著;而岩体破裂膨胀性对巷道围岩塑性区范围的影响不明显,但对巷道围岩变形以及破裂区范围的影响显著。
| [1] | Jiang Y, Yoneda H, Tanabashi Y. Theoretical estimation of loosening pressure on tunnels in soft rocks[J]. Tunneling and Underground Space Technology, 2001, 16(2): 99–105. DOI:10.1016/S0886-7798(01)00034-7 |
| [2] | Torres C C, Fairhurst C. The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(6): 777–809. DOI:10.1016/S0148-9062(99)00047-9 |
| [3] | Wang Y L. Ground response of circular tunnel in poorly consolidated rock[J]. Journal of Geotechnical Engineering, 1996, 122(9): 703–708. DOI:10.1061/(ASCE)0733-9410(1996)122:9(703) |
| [4] |
袁文伯, 陈进.
软化岩层中巷道的塑性区与破碎区分析[J]. 煤炭学报, 1986, 23(3): 77–85.
YUAN Wenbo, CHEN Jin. Analysis of plastic zone and loose zone around opening in softening rock mass[J]. Journal of China Coal Society, 1986, 23(3): 77–85. (in Chinese) |
| [5] |
马念杰, 张益东.
圆形巷道围岩变形压力新解法[J]. 岩石力学与工程学报, 1996, 15(1): 84–89.
MA Nianjie, ZHANG Yidong. A new analysis on ground pressures around openings[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(1): 84–89. (in Chinese) |
| [6] |
姚国圣, 李镜培, 谷拴成.
考虑岩体扩容和塑性软化的软岩巷道变形解析[J]. 岩土力学, 2009, 30(2): 463–467.
YAO Guosheng, LI Jjingpei, GU Shuancheng. Analytic solution to deformation of soft rock tunnel considering dilatancy and plastic softening of rock mass[J]. Rock and Soil Mechanics, 2009, 30(2): 463–467. (in Chinese) |
| [7] |
高召宁, 孟祥瑞, 赵光明.
煤层底板变形与破坏规律直流电阻率CT探测[J]. 重庆大学学报, 2011, 34(8): 90–96.
GAO Zhaoning, MENG Xiangrui, ZHAO Guangming. DC electrical resistivity CT survey of deformation and damage law of coal floor[J]. Journal of Chongqing University, 2011, 34(8): 90–96. DOI:10.11835/j.issn.1000-582X.2011.08.016 (in Chinese) |
| [8] |
张常光, 张庆贺, 赵均海.
考虑应变软化、剪胀和渗流的水工隧洞解析解[J]. 岩土工程学报, 2009, 31(12): 1942–1946.
ZHANG Changguang, ZHANG Qinghe, ZHAO Junhai. Analytical solutions of hydraulic tunnels considering strain softening, shear dilation and seepage[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1942–1946. (in Chinese) |
| [9] |
张常光, 胡云世, 赵均海, 等.
深埋圆形水工隧洞弹塑性应力和位移统一解[J]. 岩土工程学报, 2010, 32(11): 1739–1745.
ZHANG Changguang, HU Yunshi, ZHAO Junhai, et al. Elastic-plastic unified solutions for stresses and displacements of a deep buried circular hydraulic tunnel[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1739–1745. (in Chinese) |
| [10] |
荣传新, 程桦.
地下水渗流对巷道围岩稳定性影响的理论解[J]. 岩石力学与工程学报, 2004, 23(5): 741–744.
RONG Chuanxin, CHENG Hua. Stability analysis of rocks around tunnel with ground water permeation[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 741–744. (in Chinese) |
| [11] |
吕晓聪, 许金余.
海底圆形隧道在渗流场影响下的弹塑性解[J]. 工程力学, 2009, 26(2): 216–221.
LU Xiaocong, XU JIinxu. Elastic-plastic solution for subsea circular tunnel under the influence of seepage field[J]. Engineering Mechanics, 2009, 26(2): 216–221. (in Chinese) |
| [12] |
刘成学, 杨林德, 李鹏.
考虑应力重分布的深埋圆形透水隧洞弹塑性解[J]. 工程力学, 2009, 26(2): 16–20.
LIU Chengxue, YANG Linde, LI Peng. Elastic-plastic analytical solution of deep buried circle tunnel considering stress redistribution[J]. Engineering Mechanics, 2009, 26(2): 16–20. (in Chinese) |
| [13] |
王星华, 章敏, 王随新.
考虑渗流及软化的海底隧道围岩弹塑性分析[J]. 岩土力学, 2009, 30(11): 3267–3272.
WANG Xinghua, ZHANG Min, WANG Suixin. Elasto-plastic analysis of surrounding rocks of subsea tunnel with consideration of seepage and material softening[J]. Rock and Soil Mechanics, 2009, 30(11): 3267–3272. DOI:10.3969/j.issn.1000-7598.2009.11.008 (in Chinese) |
| [14] |
李宗利, 任青文, 王亚红.
考虑渗流场影响深埋圆形隧洞的弹塑性解[J]. 岩石力学与工程学报, 2004, 23(8): 1291–1295.
LI Zongli, REN Qingwei, WANG Yahong. Elasto-plastic analytical solution of deep-buried circle tunnel considering fluid flow field[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1291–1295. (in Chinese) |
| [15] |
付国彬.
巷道围岩破裂范围与位移的新研究[J]. 煤炭学报, 1995, 20(3): 304–310.
FU Guobin. Recent investigation of extent of fractured zone and displacement of rocks around the roadways[J]. Journal of China Coal Society, 1995, 20(3): 304–310. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


