可靠性是数控机床性能的重要指标,对数控机床的可靠性进行评估是机床可靠性工作的重要内容。常见的数控机床可靠性评估立足于普通更新理论[1-3]和非齐次随机过程[4-5],两者分别对应完全维修和最小维修。前者假设机床经维修后可以恢复到最初始的“如新状态”,而后者则认为机床经维修后恢复到故障发生前的“如旧状态”。然而在现实中,大多数控机床在维修后不会处于这2种极端状态,而是处于一种中间状态,即维修是不完全的。目前,对不完全维修条件下的数控机床可靠性评估的研究相对较少,而且研究方法集中于Kijima模型即广义更新过程。其中,文献[6-7]对单台和多台数控机床的Kijima模型Ⅰ、Ⅱ进行了分析,并应用非线性约束规划方法求解模型参数;文献[8]利用Kijima Ⅰ对数控机床子系统可靠性进行了建模分析,并应用遗传算法对模型参数进行求解。但是,应用Kijima模型进行机床可靠性评估不仅参数求解复杂,最为不便的是研究者无法通过模型直接得出可靠性指标如失效强度、MTBF等,而是需要借助模拟如Monte Carl的方法[9]间接求得,限制了其工程应用。
为此,文中提出利用广义比例强度模型(GPIM)对数控机床的可靠性进行评估。该模型能够像广义更新过程一样,在评估时考虑到维修活动的影响,所不同的是模型参数求解容易,并且能够直接得出机床可靠性指标。
1 基于GPIM的故障数据建模 1.1 基于GPIM的维修影响因子分析GPIM由H.Guo[10]首先提出,其故障强度函数为
| $ \lambda \left( t \right) = \lambda \beta {t^{\beta - 1}}\exp \left[ {\gamma N\left( t \right)} \right]。$ | (1) |
GPIM认为,每次维修会使产品故障强度发生变化,维修对产品可靠性的累积影响通过γN(t)来反映。在此,文中称γ为修复功效因子。当γ<0时,表示维修对产品可靠性有改善作用;当γ=0时,表示维修对产品可靠性没有显著的影响;当γ>0时,表示维修使产品可靠性恶化。
为了便于参数与可靠性指标的估计,H.Guo提出用累积故障数目m(t)来近似,为
| $ \lambda \left( t \right) = \lambda \beta {t^{\beta - 1}}\exp \left[ {\gamma m\left( t \right)} \right], $ |
进而可以得到
| $ \left\{ \begin{array}{l} \lambda \left( t \right) = \frac{{\lambda \beta {t^{\beta - 1}}}}{{1 - \gamma \lambda {t^\beta }}},\\ m\left( t \right) = - \frac{1}{\gamma }\ln \left( {1 - \gamma \lambda {t^\beta }} \right)。\end{array} \right. $ | (2) |
设单台机床在时间区间[0,T]内的故障发生时刻为t1,t2,…,tn,当tn=T时为故障截尾试验,tn<T时为时间截尾试验。因此,故障时间ti的条件概率密度函数为
| $ f\left( {{t_i}\left| {{t_{i - 1}}} \right.} \right) = \lambda \beta {t^{\beta - 1}}{{\rm{e}}^{\left( {i - 1} \right)\gamma }}\exp \left[ { - \lambda \left( {t_i^\beta - t_{i - 1}^\beta } \right){{\rm{e}}^{\left( {i - 1} \right)\gamma }}} \right], $ |
所以,机床故障时间的似然函数为
| $ \begin{array}{*{20}{c}} {L = \prod\limits_{i \in F} {f\left( {{t_i}\left| {{t_{i - 1}}} \right.} \right)} \prod\limits_{i \in C} {R\left( {T\left| {{t_n}} \right.} \right)} = }\\ {{{\left( {\lambda \beta } \right)}^n}\exp \left[ {\frac{{n\left( {n - 1} \right)}}{2}\gamma - \lambda {{\rm{e}}^{n\gamma }}\left( {{T^\beta } - t_n^\beta } \right)} \right] \times }\\ {\prod\limits_{i = 1}^n {t_i^{\beta - 1}\exp \left[ { - \lambda {{\rm{e}}^{\left( {i - 1} \right)\gamma }}\left( {t_i^\beta - t_{i - 1}^\beta } \right)} \right],} } \end{array} $ |
式中:R(·)为机床条件可靠度函数;F为故障数据集;C为时间截尾数据集。
两边取对数得其对数似然函数表达式为
| $ \begin{array}{*{20}{c}} {\ln L = n\left( {\ln \lambda + \ln \beta } \right) + \frac{{n\left( {n - 1} \right)}}{2}\gamma - }\\ {\lambda {{\rm{e}}^{n\gamma }}\left( {{T^\beta } - t_n^\beta } \right) + \left( {\beta - 1} \right)\sum\limits_{i = 1}^n {{t_i}} - \lambda \sum\limits_{i = 1}^n {{{\rm{e}}^{\left( {i - 1} \right)\gamma }}\left( {t_i^\beta - t_{i - 1}^\beta } \right)} ,} \end{array} $ |
因此,对于k台机床来说,其对数似然函数为
| $ \begin{array}{*{20}{c}} {\ln L = \sum\limits_{i = 1}^k {{n_i}\left( {\ln \lambda + \ln \beta } \right)} + }\\ {\sum\limits_{i = 1}^k {\left( {\frac{{{n_i}\left( {{n_i} - 1} \right)}}{2}\gamma - \lambda {{\rm{e}}^{{n_i}\gamma }}\left( {T_i^\beta - t_{{n_i}}^\beta } \right)} \right)} + }\\ {\left( {\beta - 1} \right)\sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{n_i}} {{t_{ij}}} } - \lambda \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{n_i}} {{{\rm{e}}^{\left( {j - 1} \right)\gamma }}\left( {t_{ij}^\beta - t_{i - 1,j}^\beta } \right)} } ,} \end{array} $ | (3) |
式中:Ti为第i台机床的截尾时间(i=1,2,…,k);ni为第i台机床的故障数;tij为第i台机床的第j个故障。
式(3)为基于GPIM的多台故障数据融合建模函数式。
1.3 GPIM模型参数的点估计与区间估计式(3)分别对λ,β,γ求偏导并令其为0,得
| $ \left\{ \begin{array}{l} \frac{{\partial \ln L}}{{\partial \lambda }} = \frac{n}{\lambda } - \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{n_i}} {{{\rm{e}}^{\left( {j - 1} \right)\gamma }}\left( {t_{ij}^\beta - t_{i - 1,j}^\beta } \right)} } - \\ \;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{{n_i}\gamma }}\left( {T_i^\beta - t_{{n_i}}^\beta } \right) = 0,\\ \frac{{\partial \ln L}}{{\partial \beta }} = \frac{n}{\beta } + \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{n_i}} {{t_{ij}}} } - \\ \;\;\;\;\;\;\;\lambda \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{n_i}} {{{\rm{e}}^{\left( {j - 1} \right)\gamma }}\left( {t_{ij}^\beta \ln {t_{ij}} - t_{i - 1,j}^\beta \ln {t_{i - 1,j}}} \right)} } - \\ \;\;\;\;\;\;\;\lambda \sum\limits_{i = 1}^k {{{\rm{e}}^{{n_i}\gamma }}\left( {T_i^\beta \ln {T_i} - t_{{n_i}}^\beta \ln {t_{{n_i}}}} \right) = 0} ,\\ \frac{{\partial \ln L}}{{\partial \gamma }} = \sum\limits_{i = 1}^k {\frac{{{n_i}\left( {{n_i} - 1} \right)}}{2} - } \\ \;\;\;\;\;\;\;\lambda \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{n_i}} {\left( {j - 1} \right){{\rm{e}}^{\left( {j - 1} \right)\gamma }}\left( {t_{ij}^\beta - t_{i - 1,j}^\beta } \right)} } - \\ \;\;\;\;\;\;\;\lambda \sum\limits_{i = 1}^k {{n_i}{{\rm{e}}^{{n_i}\gamma }}\left( {T_i^\beta - t_{{n_i}}^\beta } \right) = 0} 。\end{array} \right. $ |
求解上式方程组可得出GPIM参数的极大似然点估计值。
GPIM参数的区间值可利用最大似然估计值的渐近对数正态分布特性[11]进行估计,对参数θ有
| $ C{B_\theta } = \theta \exp \left( { \pm {z_{\alpha /2}}\sqrt {{\mathop{\rm var}} \theta } /\theta } \right), $ | (4) |
式中,zα/2为置信度,是100(1-α)%的标准正态分布的分位数。
当式(4)的参数为λ,β,γ,其方差及协方差由逆Fisher信息矩阵[11]为
| $ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {{\mathop{\rm var}} \left( \lambda \right)}&{{\mathop{\rm cov}} \left( {\lambda ,\beta } \right)}&{{\mathop{\rm cov}} \left( {\lambda ,\gamma } \right)}\\ {{\mathop{\rm cov}} \left( {\lambda ,\beta } \right)}&{{\mathop{\rm var}} \left( \beta \right)}&{{\mathop{\rm cov}} \left( {\beta ,\gamma } \right)}\\ {{\mathop{\rm cov}} \left( {\lambda ,\gamma } \right)}&{{\mathop{\rm cov}} \left( {\beta ,\gamma } \right)}&{{\mathop{\rm var}} \left( \gamma \right)} \end{array}} \right) = \\ \;\;\;\left( {\begin{array}{*{20}{c}} { - \frac{{{\partial ^2}\ln L}}{{\partial {\lambda ^2}}}}&{ - \frac{{{\partial ^2}\ln L}}{{\partial \lambda \partial \beta }}}&{ - \frac{{{\partial ^2}\ln L}}{{\partial \lambda \partial \gamma }}}\\ { - \frac{{{\partial ^2}\ln L}}{{\partial \lambda \partial \beta }}}&{ - \frac{{{\partial ^2}\ln L}}{{\partial {\beta ^2}}}}&{ - \frac{{{\partial ^2}\ln L}}{{\partial \beta \partial \gamma }}}\\ { - \frac{{{\partial ^2}\ln L}}{{\partial \lambda \partial \gamma }}}&{ - \frac{{{\partial ^2}\ln L}}{{\partial \beta \partial \gamma }}}&{ - \frac{{{\partial ^2}\ln L}}{{\partial {\gamma ^2}}}} \end{array}} \right)_{\begin{array}{*{20}{c}} {\lambda = \hat \lambda ;}\\ {\beta = \hat \beta ;}\\ {\gamma = \hat \gamma 。} \end{array}}^{ - 1}。\end{array} $ |
利用上式结果,将λ,β,γ代入式(4),可得出GPIM参数的区间估计。
2 数控机床可靠性指标的估计 2.1 数控机床可靠性指标的点估计机床可靠性指标能够对机床可靠性的变化给出定量的描述。GPIM参数求解后就可以对机床的各种可靠性参数进行计算。这里给出2类可靠性指标:
1) 瞬时故障强度函数λ(t)与瞬时MTBFu(t);
2) 累积故障强度λc(t)、累积平均无故障工作时间uc(t)与累积故障数m(t)。其中,累积平均无故障工作时间uc(t)即是客户能够感受到的平均无故障工作时间MTBF。
将λ,β,γ的极大似然估计值代入式(2),便能够得出瞬时故障强度函数λ(t)与累积故障数m(t)的点估计。
由
| $ u\left( t \right) = \frac{{1 - \hat \lambda \hat \gamma {t^{\hat \beta }}}}{{\hat \lambda \hat \beta {t^{\hat \beta - 1}}}}, $ |
由
| $ {u_c}\left( t \right) = - \frac{{\hat \gamma t}}{{\ln \left( {1 - \hat \lambda \hat \gamma {t^{\hat \beta }}} \right)}}, $ |
进而,可由
采用Delta方法[12]对以上可靠性指标进行区间估计。
设▽为参数λ,β,γ的函数,则▽的方差为
| $ \begin{array}{*{20}{c}} {{\mathop{\rm var}} \left( \nabla \right) = {{\left( {\frac{{\partial \nabla }}{{\partial \lambda }}} \right)}^2}{\mathop{\rm var}} \left( {\hat \lambda } \right) + {{\left( {\frac{{\partial \nabla }}{{\partial \beta }}} \right)}^2}{\mathop{\rm var}} \left( {\hat \beta } \right) + }\\ {{{\left( {\frac{{\partial \nabla }}{{\partial \gamma }}} \right)}^2}{\mathop{\rm var}} \left( {\hat \gamma } \right) + 2\left( {\frac{{\partial \nabla }}{{\partial \lambda }}} \right)\left( {\frac{{\partial \nabla }}{{\partial \beta }}} \right){\mathop{\rm cov}} \left( {\hat \lambda ,\hat \beta } \right) + }\\ {2\left( {\frac{{\partial \nabla }}{{\partial \lambda }}} \right)\left( {\frac{{\partial \nabla }}{{\partial \gamma }}} \right){\mathop{\rm cov}} \left( {\hat \lambda ,\hat \gamma } \right) + 2\left( {\frac{{\partial \nabla }}{{\partial \beta }}} \right)\left( {\frac{{\partial \nabla }}{{\partial \gamma }}} \right){\mathop{\rm cov}} \left( {\hat \beta ,\hat \gamma } \right),} \end{array} $ |
从而,▽的区间亦可由式(4)求出。
当▽分别为λ(t)、m(t)、λc(t)、u(t)和uc(t),便可以得出相应可靠性指标的区间估计。
3 故障趋势检验与修复功效检验为了对GPIM模型的有效性进行验证,采用似然比检验法[12]对故障趋势与修复功效检验。
3.1 故障趋势检验原假设H0:故障过程不存在显著故障趋势(β=1)。备选假设H1:故障过程存在显著故障趋势(β≠1)。统计检验量为
| $ {\mathit{\Lambda }_1} = - 2\ln \frac{{L\left( {\beta = 1;\lambda ,\gamma } \right)}}{{L\left( {\lambda ,\beta ,\gamma } \right)}}\sim\chi _1^2。$ |
对于给定的显著水平α,当Λ1值大于临界值K时,拒绝原假设;否则,接受原假设;以下同此。
3.2 修复功效检验原假设H0:维修活动对机床可靠性无显著影响(γ=0)。备选假设H1:维修活动使机床可靠性改善或恶化(γ≠0)。统计检验量为
| $ {\mathit{\Lambda }_2} = - 2\ln \frac{{L\left( {\gamma = 0;\lambda ,\beta } \right)}}{{L\left( {\lambda ,\beta ,\gamma } \right)}}\sim\chi _1^2。$ |
原假设H0:机床故障过程无明显趋势且维修活动无明显作用(β=1且γ=0)。备选假设H1:至少有一种影响存在(β≠1或γ≠0)或同时存在(β≠1且γ≠0)。统计检验量为
| $ {\mathit{\Lambda }_3} = - 2\ln \frac{{L\left( {\beta = 1,\gamma = 0;\lambda } \right)}}{{L\left( {\lambda ,\beta ,\gamma } \right)}}\sim\chi _2^2。$ |
文献[3]给出了4台数控机床的28个故障数据,并用寿命分布分析方法(完全维修)对数据进行了分析,结论认为:故障数据优先符合威布尔分布;文献[5, 7]分别采用非齐次泊松过程方法(最小维修)与广义更新过程方法(不完全维修)对文献[3]的数据进行了分析并对以上3种方法进行了比较,结论认为:非齐次泊松过程(NHPP)方法优于威布尔分布,广义更新过程得出的结果与非齐次泊松过程一致。现用文中提出的GPIM模型对这4台机床的故障数据进行分析。
4.1 基于AIC和BIC准则的模型优选在应用GPIM对4台机床进行可靠性分析之前,首先根据AIC[13](akaike information criterion)和BIC[14](bayesian information criterion)信息准则将GPIM与其他模型进行比较。AIC和BIC利用了似然估计性质是模型选择的有效方法之一。该准则认为最佳模型应有最小的AIC和BIC值,其表达式定义为
| $ {\rm{AIC}} = - 2\max \ln L + 2m, $ |
| $ {\rm{BIC}} = - 2\max \ln L + m\ln n, $ |
式中:m为模型参数的个数;n为观测数据的个数;max ln L为故障数据的最大对数似然函数。
各模型的计算结果如表 1所示。
| 表 1 各模型计算结果 |
由表 1可知,Weibull分布表明机床近似处于偶然期,而最小维修和不完全维修条件下的模型均表明机床处于可靠性增长阶段。此外,-lnL、AIC和BIC结果显示GPIM为最佳模型。
4.2 模型参数及可靠性指标计算求解参数偏导方程组并利用Fisher信息矩阵计算出模型参数的点估计与置信度为90%的置信区间,见表 2所示。
| 表 2 模型参数点估计与区间估计 |
因此,机床的瞬时与累积的可靠性指标如下:瞬时可靠性指标为
| $ \left\{ \begin{array}{l} \lambda \left( t \right) = \frac{{2.031\;9 \times {{10}^{ - 2}}{t^{ - 0.076\;4}}}}{{1 + 6.969\;6 \times {{10}^{ - 3}}{t^{0.923\;6}}}},\\ u\left( t \right) = 0.343t + 49.214\;5{t^{0.076\;4}}, \end{array} \right. $ |
累积可靠性指标为
| $ \left\{ \begin{array}{l} {\lambda _c}\left( t \right) = 3.156\;6{t^{ - 1}}\ln \left( {1 + 6.969\;6 \times {{10}^{ - 3}}{t^{0.923\;6}}} \right),\\ {u_c}\left( t \right) = \frac{{0.316\;8t}}{{\ln \left( {1 + 6.969\;6 \times {{10}^{ - 3}}{t^{0.923\;6}}} \right)}},\\ m\left( t \right) = 3.156\;6\ln \left( {1 + 6.969\;6 \times {{10}^{ - 3}}{t^{0.923\;6}}} \right)。\end{array} \right. $ |
当t=1 500时的可靠性指标点估计与置信度90%的置信区间,见表 3所示。
| 表 3 可靠性指标点估计与区间估计 |
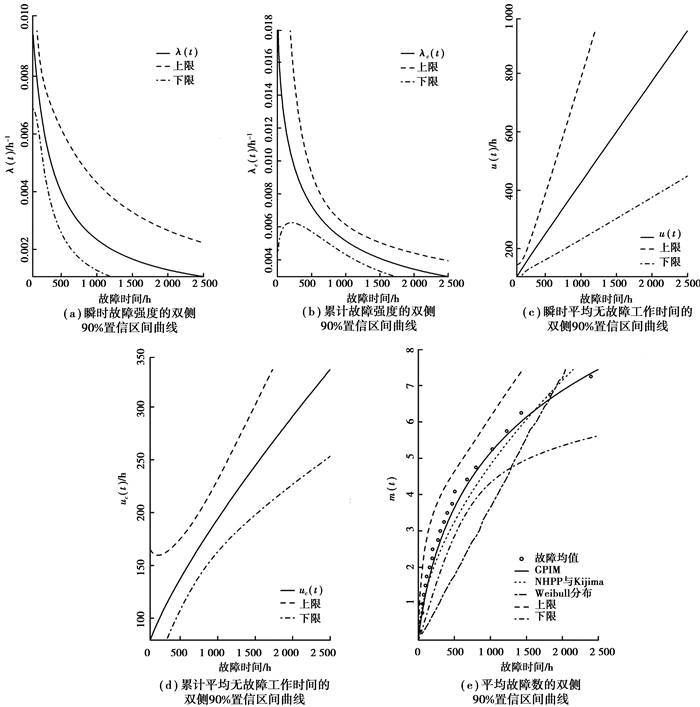
图 1为机床瞬时与累积可靠性指标置信度90%的双侧区间图。
|
图 1 可靠性指标的双侧90%置信区间曲线 |
图 1(e)可以看出,GPIM模型曲线较好地拟合了4台机床的实际故障均值;图 1(a)与图 1(b)显示故障强度整体呈下降趋势,表明机床的可靠性得到改善;图 1(c)与图 1(d)对比表明,尽管到后期(如t=1 500 h)瞬时MTBF能够达到600 h以上,但累积MTBF只有250 h左右,说明早期故障降低了机床整体在客户使用时的可靠性表现水平,建议生产商在机床出厂前加强早期故障消除技术。
4.3 模型检验与讨论故障趋势检验与修复功效检验的结果如表 4所示。
| 表 4 故障趋势与修复功效检验结果 |
1) 表 4故障趋势结果表明,所评估的4台数控机床故障过程具有显著的趋势,这与最小维修和Kijima模型Ⅰ、Ⅱ以及图 1(a)、图 1(b)的结论一致。
2) 修复功效结果表明,对4台数控机床进行的维修活动是积极的,它对机床可靠性的改善作用显著;这一结论与广义更新过程(Kijima模型Ⅰ、Ⅱ)所得出的结论修复功效因子q=1.000 0不同。广义更新过程q=1.000 0,表示维修活动只是将机床恢复到了故障前的状态(最小维修),而没有使机床的可靠性比故障前的状态得到改善,换句话说,维修活动的作用是不显著的。由于从模型拟合优度比较结果来看,对该例GPIM优于广义更新过程,这里认为修复功效显著。
3) 协同检验结果表明,有足够的理由拒绝原假设。与此同时,综合故障趋势、修复功效检验结果和GPIM模型的拟合度来看,认为二者协同作用于机床故障过程是合理的。
5 结论数控机床是典型的可修复系统,在对数控机床进行可靠性评估时,维修活动是要进行考虑的重要影响因子。相比于完全维修和最小维修,不完全维修更符合机床的实际状况。文中提出了利用广义比例强度模型(GPIM)对不完全维修条件下的机床可靠性进行评估,给出了模型参数和可靠性指标的点估计与区间估计。通过对4台数控机床的实例分析表明,GPIM模型得出的结果要优于其他的方法和模型。此外,广义更新过程对实例分析得出了与GPIM有差异性的结论,说明了对二者的对比研究非常有必要,这也是笔者接下的研究方向。
| [1] | Jia Y Z, Wang M L, Jia Z X. Probability distribution of machining center failure[J]. Reliability Engineering and System Safety, 1995, 50(1): 121–125. DOI:10.1016/0951-8320(95)00070-I |
| [2] | Dai Y, Zhou Y F, Jia Y Z. Distribution of time between failures of machining center based on type Ⅰ censored data[J]. Reliability Engineering and System Safety, 2003, 79(3): 377–379. DOI:10.1016/S0951-8320(02)00243-0 |
| [3] |
张英芝, 贾亚洲, 申桂香, 等.
基于随机截尾的数控机床故障分布模型研究[J]. 系统工程理论与实践, 2005, 2(2): 134–138.
ZHANG Yingzhi, JIA Yazhou, SHEN Guixiang, et al. Research on model of failure distribution for numerical machine with random ending method[J]. Systems Engineering-Theory & Practice, 2005, 2(2): 134–138. (in Chinese) |
| [4] |
张英芝, 申桂香, 薛玉霞, 等.
随机截尾数控机床故障过程[J]. 吉林大学学报:工学版, 2007, 37(6): 1346–1349.
ZHANG Yingzhi, SHEN Guixiang, XUE Yuxia, et al. Failure process for numerical control machine with random ending method[J]. Journal of Jilin University:Engineering and Technology Edition, 2007, 37(6): 1346–1349. (in Chinese) |
| [5] |
王智明, 杨建国, 王国强, 等.
多台数控机床最小维修的可靠性评估[J]. 哈尔滨工业大学学报, 2011, 43(7): 127–130.
WANG Zhiming, YANG Jianguo, WANG Guoqiang, et al. Reliability assessment of multiple machine tools with minimal repair[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 127–130. DOI:10.11918/j.issn.0367-6234.2011.07.026 (in Chinese) |
| [6] | Wang Z M, Yang J G. Numerical method for Weibull generalized renewal process and its applications in reliability analysis of NC machine tools[J]. Computers & Industrial Engineering, 2012, 63(4): 1128–1134. |
| [7] | 王智明. 数控机床的可靠性评估与不完全预防维修及其应用[D]. 上海: 上海交通大学, 2011. http: //cdmd. cnki. com. cn/Article/CDMD-10248-1011298238. htm |
| [8] | 许彬彬. 基于维修程度的数控机床可靠性建模与分析[D]. 吉林: 吉林大学博士学位论文, 2011. http: //cdmd. cnki. com. cn/Article/CDMD-10183-1012257714. htm |
| [9] | Krivtsov V. A monte carlo approach to modeling and estimation of the generalized renewal process in repairable system reliability analysis[D]. Maryland:University of Maryland, College Park, 2000. |
| [10] | Guo H R, Zhao W B, Mettas A. Practical methods for modeling repairable systems with time trends and repair effects[C]//Proceedings of 2006 Annual Reliability and Maintainability Symposium, January 23-26, 2006, Newport Beach, California. Piscataway:IEEE Press, 2006:182-188. http://dl.acm.org/citation.cfm?id=1344016 |
| [11] | Nelson W. Accelerated testing:statistical methods, test plans, and data analysis[M]. New York: John Wiley & Sons, 1990. |
| [12] | Meeker W Q, Escobar L A. Statistical methods for reliability data[M]. New York: John Wiley & Sons, 1998. |
| [13] | Akaike H. A new look at statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716–723. DOI:10.1109/TAC.1974.1100705 |
| [14] | Schwarz G. Estimating the dimension of a model[J]. Annals of Statistics, 1978, 6(2): 461–464. DOI:10.1214/aos/1176344136 |
 2014, Vol. 37
2014, Vol. 37


