1b. 南京农业大学 江苏省智能化农业装备重点实验室, 南京 210031;
2. 南京航空航天大学 能源与动力工程学院, 南京 210016
1b. Jiangsu Key Laboratory for Intelligent Agricultural Equipment, Nanjing Agricultural University, Nanjing 210031, China;
2. College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
电动汽车再生制动防抱死控制系统(即再生ABS)是指驱动轮在进行再生制动时,通过对再生制动力的控制,在回收能量的同时防止驱动轮抱死的一种电磁制动系统。当电动汽车在冰雪等低附着系数路面上进行再生制动时,即使制动强度小,也极有可能使驱动轮抱死;对处在转向再生制动工况下的后驱型电动汽车,即使驱动轮不抱死,也会使其操纵稳定性严重降低。Shin-ichiro Sakai等[1]利用模型跟随控制法对再生ABS和液压ABS进行了对比分析,结果表明再生ABS比液压ABS的反应速度快,控制精度高;Yoichi Hori等[2]对再生ABS分别运用滑移率控制法和模型跟随控制法进行对比研究,仿真结果表明滑移率控制法的控制精度高;Khatun P等[3]研究了再生ABS的模糊控制性能;Tur,O等[4]基于simplorer仿真软件对比分析了再生ABS与液压ABS的制动性能,表明了再生ABS的反应速度快于液压ABS;Min-Hung Hsiao等[5]利用蓄电池与超级电容器的串、并联组合,利用滑模控制建立了离散型再生ABS模型。Chunting Mi等[6]利用迭代学习控制法设计了再生ABS防滑控制器。陈庆樟、赵国柱等[7-8]利用简化的电机模型建立了再生ABS滑模变结构控制模型。
无刷直流电机是电动汽车目前最适合的动力装置[9]。PWM调制方案有单、双管调制2种类型[10]。不同的PWM调制方案对无刷直流电机电动汽车再生ABS的制动性能是否有影响,影响有多大,目前却鲜见有此方面的研究报道。文章以无刷直流电机电动汽车为研究对象,建立其单轮车辆动力学模型,通过仿真方法对比分析该型电动汽车再生ABS性能的差异,以期对该型车辆再生ABS的设计具有一定的工程指导意义。
1 无刷直流电机再生制动原理 1.1 单管PWM调制下的再生制动机理无刷直流电机再生制动在单管PWM调制模式下,任何时刻只有一个功率开关管工作,如图 2所示,在某个60°电角度期间,只有VT2、VT4、VT6 3个管中一个管有开关动作,其他管均关闭[11]。由于每个60°电角度区间内,虽通电绕组与导通的功率管会随转子位置变化而依次轮换,但任何时刻均只有2组绕组通电,起作用的开关管也始终只有一个,而且电机的各种波形与电压方程式也均相同。因此,只需分析电机在一个60°电角度区间内的再生制动原理。当VT4闭合时,电流沿图 1中路径①流动,该电流方向与电机驱动时(以下简称“电动时”)相反,故电磁力矩产生制动作用。此时,反电动势产生的电能除一部分变成回路的电阻热外,其余全部变成磁场能储存于回路绕组电感中,故称此阶段制动为蓄能制动。忽略VT4、D6的管压降,电压方程为
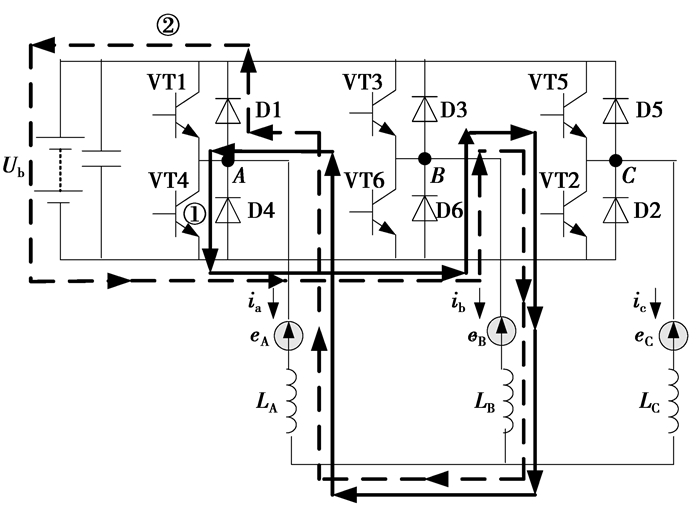
|
图 1 单管PWM调制时某60°电角度区间再生制动电流路径 |
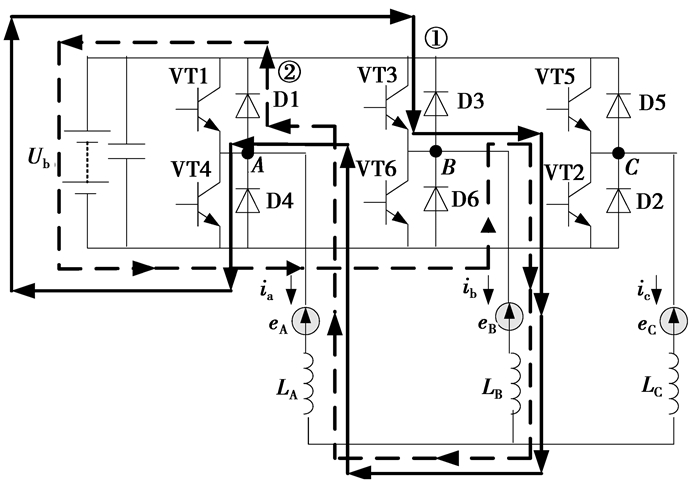
|
图 2 双管PWM调制时某60°电角度区间电气制动电流路径 |
| $ 0 = {E_{\rm{a}}} + {i_{\rm{a}}}R + {L_{\rm{a}}}\frac{{{\rm{d}}{i_{\rm{a}}}}}{{{\rm{d}}t}}, $ |
式中:Ea为电机反电势;ia为电枢电流;R为回路电阻;La为回路电感。
当VT4截止时,电枢绕组电流不能突变,电流沿图 1中路径②流动。该电流方向仍与电动时相反,故电磁力矩仍然对电机产生制动效果。此时反电动势产生的电能和VT4闭合期间储存于回路电感的磁场能,除部分变成回路的电阻热外,其余均回充到蓄电池中,故称此制动为回馈制动,忽略D1、D6的管压降,电压方程为
| $ {U_{\rm{b}}} = {E_{\rm{a}}} + {i_{\rm{a}}}R + {L_{\rm{a}}}\frac{{{\rm{d}}{i_{\rm{a}}}}}{{{\rm{d}}t}}, $ | (2) |
式中Ub为电源端电压。
1.2 双管调制下的再生制动机理双管调制是指任何时刻有2个开关管同步工作。与单管调制一样,也只分析某个60°电角度内再生制动原理。调制方案如图 2所示。
当VT3、VT4同时导通时,在电源与反电动势共同作用下,电流沿图 2中路径①流动。该电流方向与电动时相反,电磁力矩对电机产生制动效果。此时从电源流出的电能以及反电动势产生的电能除一部分变成回路电阻热外,其余全部变成磁场能而储存于回路电感中。此时相当于电源反接,故称此制动为反接制动。忽略VT3、VT4的管压降,电压方程为
| $ {U_{\rm{b}}} = {E_{\rm{a}}} + {i_{\rm{a}}}R + {L_{\rm{a}}}\frac{{{\rm{d}}{i_{\rm{a}}}}}{{{\rm{d}}t}}。$ | (3) |
设电机驱动时电枢电流流向为正方向,则制动时电枢电流ib为负,即ib=ia。单管调制下,当电枢电流处于稳态时,在每个PWM周期T内,电枢电流在制动电流指令值上下波动,蓄能制动阶段与回馈制动阶段电流变化率的绝对值之比与每个阶段所占时间成反比,根据该关系,并考虑到制动电流的方向性有
| $ {i_{\rm{b}}} = \frac{{{E_{\rm{a}}} - \left( {1 - \alpha } \right){U_{\rm{b}}}}}{R}, $ | (4) |
同理,可得双管调制下稳态时电机制动电流为
| $ {i_{\rm{b}}} = \frac{{\left( {2\alpha - 1} \right){U_{\rm{b}}} + {E_{\rm{a}}}}}{R}, $ | (5) |
因此,再生ABS工作时,调节占空比α,即可调节电机制动力矩使驱动轮具有最佳滑移率。
2 单轮车辆再生制动动力学建模以单轮车辆模型为例,忽略制动时载荷转移,其受力分析如图 3所示,再生制动动力学模型为
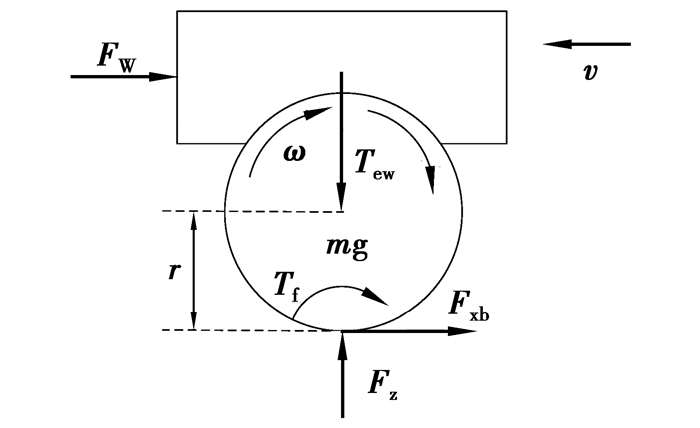
|
图 3 单轮车辆再生制动时的受力分析 |
| $ m\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = {F_{{\rm{xb}}}} - {F_{\rm{W}}} - {F_{\rm{f}}}, $ | (6) |
| $ {J_{\rm{W}}}{{\dot \omega }_{\rm{W}}} = {T_{{\rm{eW}}}} - {F_{{\rm{xb}}}}r - {T_{\rm{f}}}, $ | (7) |
式中:m为单轮车辆质量;v为车辆纵向速度;Fxb为地面制动力;FW为空气阻力;Ff为滚动阻力;JW为车轮转动惯量;ωW为车轮角速度;TeW为驱动轮受到的再生制动力矩;r为车轮半径;Tf为滚动阻力偶。
地面制动力为
| $ {F_{{\rm{xb}}}} = mg\mu \left( \lambda \right), $ | (8) |
式中:g为重力加速度;μ(λ)为附着系数;λ为车轮滑移率。
空气阻力为
| $ {F_{\rm{w}}} = 0.5{C_{\rm{D}}}A\rho {v^2}, $ | (9) |
式中:CD为空气阻力系数;A为迎风面积;ρ为空气密度。
滚动阻力为
| $ {F_{\rm{f}}} = \frac{{{F_{\rm{f}}}}}{r} = mg{f_{\rm{r}}}, $ | (10) |
式中fr为滚动阻力系数。
驱动轮受到的再生制动力矩为
| $ {T_{{\rm{eW}}}} = {T_{\rm{e}}}{i_{\rm{g}}}/2, $ | (11) |
式中:ig为轮边减速器传动比;Te为电机再生制动力矩,其大小为
| $ {T_{\rm{e}}} = {k_{\rm{t}}}{i_{\rm{b}}}, $ | (12) |
式中kt为电机力矩常数。
转速传动关系为
| $ {\omega _{\rm{W}}} = \frac{{{\omega _{\rm{m}}}}}{{{i_{\rm{g}}}}}, $ |
式中ωm为电机机械角速度。
将式(8)至式(13)代入方程(7)与(8)整理得
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = {\rm{g}}\mu \left( \lambda \right) - \frac{{\rho {C_{\rm{D}}}A{V^2}}}{{2m}} - {\rm{g}}{f_{\rm{r}}},\\ \frac{{{\rm{d}}{\omega _{\rm{W}}}}}{{{\rm{d}}t}} = \frac{{{i_{\rm{g}}}{k_{\rm{t}}}{i_{\rm{b}}}}}{{2{J_{\rm{W}}}}} - \frac{{m{\rm{g}}{f_{\rm{r}}}}}{{{J_{\rm{W}}}}} - \frac{{m{\rm{g}}r}}{{{J_{\rm{W}}}}}\mu \left( \lambda \right)。\end{array} \right. $ | (14) |
设x1=v/r,x2=ωW,f1=g/r,f2=ρCDAr/(2m),f3=gfr/r,f4=igkt/(2JW),f5=mgfrr/JW,f6=mgr/JW,u=ib。则式(14)变为
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {f_1}\mu \left( \lambda \right) - {f_2}x_1^2 - {f_3},\\ {{\dot x}_2} = - {f_5} - {f_6}\mu \left( \lambda \right) + {f_4}u。\end{array} \right. $ | (15) |
这里轮胎模型为[12]
| $ \mu \left( \lambda \right) = \frac{{2{\mu _{\rm{p}}}{\lambda _{\rm{p}}}\lambda }}{{\left( {\lambda _{\rm{p}}^2 + {\lambda ^2}} \right)}}, $ | (16) |
式中:μp为峰值附着系数;结冰路面μp=-0.1;λp为μp对应的滑移率;文中λp=-20%,该模型在-0.3≤λ≤0时较精确。
3 再生ABS控制器设计 3.1 外环控制器制动时滑移率λ定义为
| $ \lambda = \frac{{{\omega _{\rm{W}}} - {\omega _v}}}{{{\omega _v}}}, $ | (17) |
式中ωv=v/r。对式(17)求一阶导数,并把式(15)代入,得关于滑移率的动力学方程
| $ \dot \lambda = y + bu, $ | (18) |
其中:y=-
由式(18)知滑移率动力学模型是一个一阶单输入非线性系统。对于滑移率的控制,简单而有效的控制方法是滑动模式控制,定义切换函数为
| $ s = \lambda - {\lambda _{\rm{p}}}, $ | (19) |
式中λp为目标滑移率。对式(19)求导,并令ṡ=0,得等效控制量为[13]
| $ {u_{{\rm{eq}}}} = - \frac{{\hat y}}{{\hat b}}, $ | (20) |
式中:ŷ为y的估计值;
系统应满足达到条件
| $ \frac{1}{2}\frac{{\rm{d}}}{{{\rm{d}}t}}{s^2} \le - \eta \left| s \right|,\eta > 0, $ | (21) |
式中η为设计参数。为此,在等效控制基础上添加一个不确定控制量,即
| $ u = {{\hat b}^{ - 1}}\left[ {\hat u - k{\mathop{\rm sgn}} \left( s \right)} \right], $ | (22) |
式中
| $ k \ge \beta \left( {F + \eta } \right) + \left( {\beta - 1} \right)\left| {\hat u} \right|, $ | (23) |
式中
| $ {\rm sat}\left( {s/\varphi } \right) = \left\{ \begin{array}{l} \frac{s}{\varphi }\;\;\;\;\;\left| s \right| < \varphi ,\\ {\mathop{\rm sgn}} \left( s \right)\;\;\;\;\;\left| s \right| \ge \varphi 。\end{array} \right. $ | (24) |
最后,滑模控制器输出量含有大量的开关信号,其结果需经低通滤波才能应用。
3.2 内环控制器为使电枢电流跟踪滑移率控制器输出的指令电流,当电机转速在基速以下时,电流调节器采用滞环比较方式的PWM电流跟踪控制可获得最佳电机性能[14]。下面以电机某一相电流的控制为例说明其控制原理[15],实际电流i与指令电流i*比较后,它们的偏差输入环宽为h的滞环比较器,如图 4左图所示,当i>i*+0.5h后,滞环比较器输出负电平,如图 4右图所示,使功率开关VT1关断,VT4导通,i减小。当i≤i*时,滞环比较器仍保持负电平输出,VT1仍关断,i继续减小,一直到i<i*-0.5h时,滞环比较器翻转,输出正电平信号,使VT1导通,VT4关断,i又开始增大,直到增大到带宽的上限为止,如此循环,使得实际电流跟踪指令电流信号呈锯齿状变化。
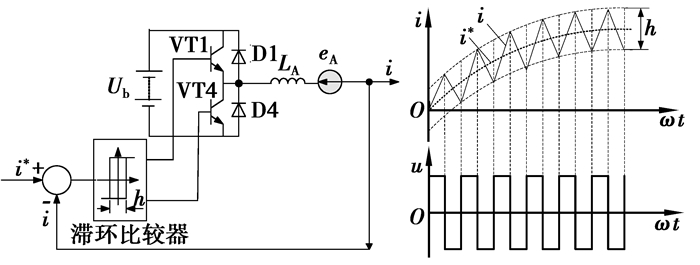
|
图 4 电流滞环跟踪控制原理图 |
以图 3所示单轮车辆模型在结冰路面上进行直线再生制动为例,对该车再生ABS分别在单、双管调制下的性能进行对比分析。相关参数如表 1所示。
| 表 1 单轮车辆仿真参数 |
仿真所用电池模型为Matlab/SimPower System中铅酸蓄电池模型,设定其初始SOC为0.6。此外,再生ABS与传统ABS一样,只在车速大于5 km/h时才起作用,当车速小于该值后,再生ABS停止工作,此后用常规机械制动系统停车,且车速很小后,为尽快停车,必须使车轮制动抱死。由于再生ABS制动时,充电电流持续时间较短,且制动之前,电池是处于放电状态,对于铅酸蓄电池,在最初的5 min内可用5C甚至8C的大电流充电而不会影响电池的使用寿命[16]。仿真结果表明:尽管由于模型的不确定性而存在建模误差,但从图 5可知2种调制方式下车辆滑移率均能稳定在目标滑移率附近,说明系统具有足够的稳定性。同时,图 5表明双管调制时,再生ABS的控制品质比单管调制时的好,正因如此,对应的制动距离也短于单管调制时的制动距离,如图 6所示。
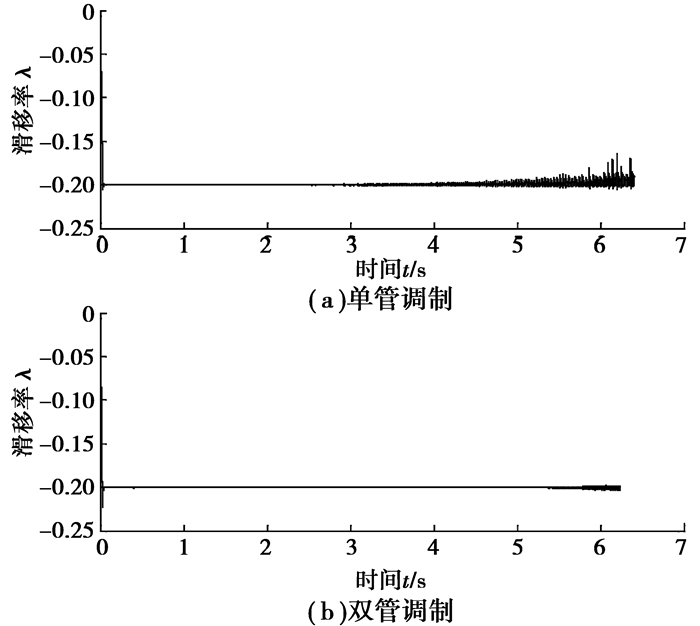
|
图 5 滑移率 |
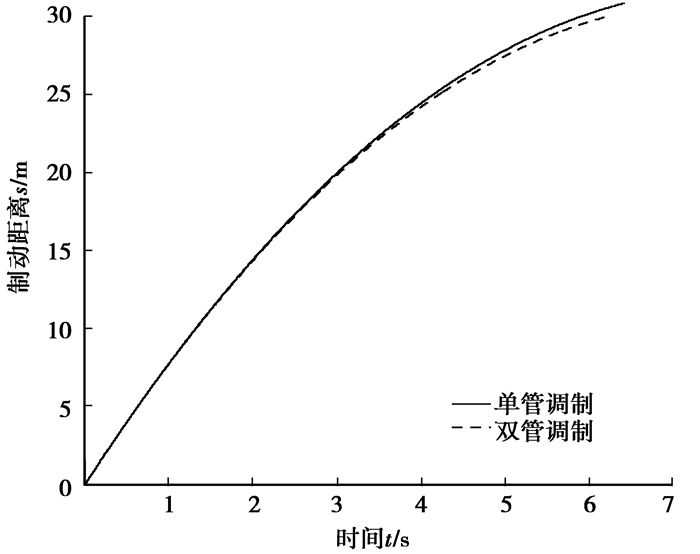
|
图 6 制动距离 |
双管调制下控制品质好的原因是由于双管调制时,电机工作于反接制动与回馈制动的交替,反接制动时,电流从蓄电池流出,如图 7(a)所示,与电机反电动势产生的发电电流叠加,并一起转化为回路电感的磁场能,增大了回馈制动阶段电枢电流,进而使回馈制动阶段电磁力矩增大,并且随着电机速度的下降,电机反电动势的降低,蓄电池端电压的上升,回馈制动充电负载增加,系统自动增大占空比,如图 7(d)所示,将延长反接制动的时间,从而提高一个PWM周期内的平均电磁力矩以满足外环的请求,因而控制品质高。而在单管调制下,电机工作于蓄能制动与回馈制动的交替,电源只接受充电,如图 7(b)所示,其蓄能制动阶段储存于回路电感的磁场能只来自于电机反动势,使回馈制动阶段的电磁力矩小于双管调制时对应阶段的电磁力矩,虽然系统也自动增大占空比来延长蓄能制动的时间,如图 7(d)所示,以满足外环对制动力矩的请求,但随着车速的降低,反电动势越来越低,蓄电池端电压却越来越高,因而产生的发电电流也就越来越小,逐渐满足不了外环的请求,因此车速越低,滑移率控制品质越差,如图 5所示。值得注意的是,双管调制时,虽然反接制动阶段电流流出蓄电池,但母线电流每隔0.1 s的平均值为负值,如图 7(c)所示,说明其电气制动性质宏观上仍是再生制动。
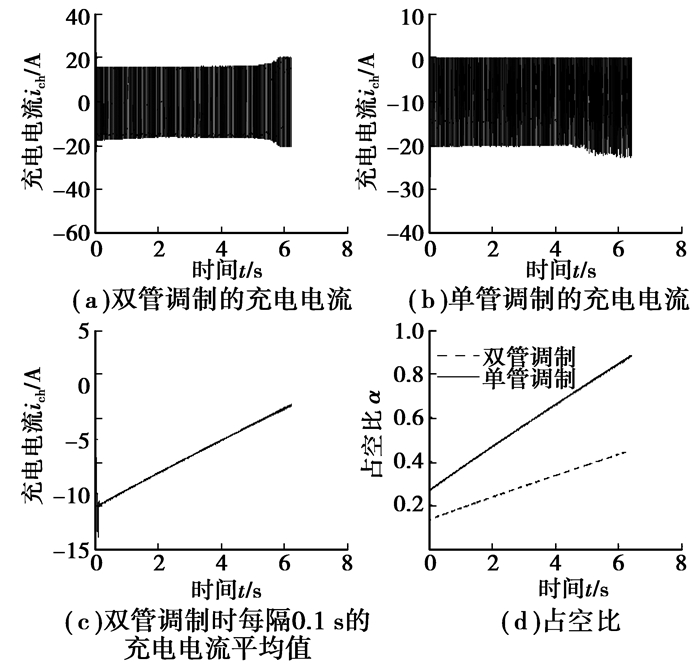
|
图 7 充电电流与占空比 |
反接制动时从电源流出的电能起到增强电机回收制动能的作用,而单管调制时,随反电势的降低与电池端电压的上升,为满足外环制动力矩的请求,蓄能制动时间越来越长,使消耗于回路电阻的热能增加,从而使得整个过程回收的能量小于双管调制,如图 8所示。
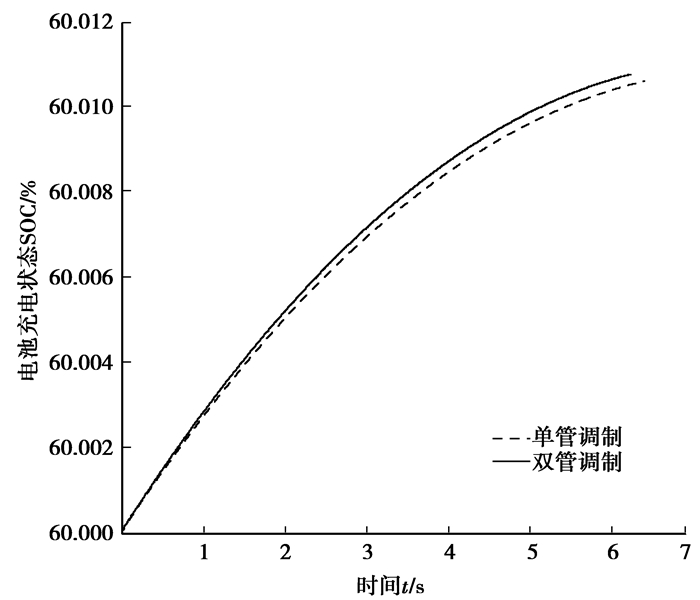
|
图 8 电池SOC |
该车再生ABS分别在单、双管调制方案下的制动距离与回馈能量如表 2所示。
| 表 2 单、双调制方案下再生ABS性能的定量差异 |
从表 2中可看出双管调制时不但能量回馈比单管调制时多了0.202 KJ,即回收量提高1.7%;更重要的是制动距离比单管调制时短了0.814 m,即制动距离缩短了2.6%,这对于提高该型电动汽车的制动安全性具有较大意义。
5 结论1) PWM调制方案对于无刷直流电机电动汽车再生ABS的制动性能有一定的影响。
2) 与单管PWM的调制相比,双管PWM调制时,无刷直流电机电动汽车再生ABS不仅回收能量多,而且制动距离缩短效果明显。
| [1] | Sakai S, Sado H, Hori Y. Anti-skid control with motor in electric vehicle[C]//Proceedings of the 6th International Workshop on Advanced Motion Control, March 30-April 01, 2000, Nagoya, Japan. Piscataway:IEEE Press, 2000:317-322. http://ieeexplore.ieee.org/document/862883/ |
| [2] | Horl Y. Future vehicle driven by electricity and control research on four wheel motored "UOT electric march Ⅱ"[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5): 954–962. DOI:10.1109/TIE.2004.834944 |
| [3] | Khatun P, Bingham C M, Schofield N, et al. An experimental laboratory bench setup to study electric vehicle antilock braking/traction systems and their control[C]//Proceedings of the IEEE 56th Vehicular Technology Conference, 2002, Birmingham, Alabama. Piscataway:IEEE Press, 2002, 3:1490-1494. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1040464 |
| [4] | Tur O, Ustun O, Tuncay R N. An introduction to regenerative braking of electric vehicles as anti-lock braking system[C]//Proceedings of IEEE Intelligent Vehicles Symposium, June 13-15, 2007, Istanbul, Turkey.Piscataway:IEEE Press, 2007:944-948. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4290238 |
| [5] | Hsiao M, Lin C. Antilock braking control of electric vehicles with electric brake[C]//Proceedings of the SAE 2005 World Congress & Exhibition, April 11-14, 2005, Detroit, Michigan, USA, [S.1] SAE Technical Papers, 2005:2005-01-1581. http://papers.sae.org/2005-01-1581/ |
| [6] | Mi C T, Lin H, Zhang Y. Iterative learning control of antilock braking of electric and hybrid vehicles[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2): 486–494. DOI:10.1109/TVT.2004.841552 |
| [7] |
陈庆樟, 何仁, 赵连生.
汽车能量再生制动防抱死集成控制方法研究[J]. 中国机械工程, 2009, 20(2): 245–248.
CHEN Qingzhang, HE Ren, ZHAO Liansheng. Research on vehicle anti-lock regenerative braking integrated control method[J]. China Mechanical Engineering, 2009, 20(2): 245–248. (in Chinese) |
| [8] |
赵国柱, 魏民祥, 杨正林.
电动城市客车再生ABS系统的建模与仿真[J]. 南京航空航天大学学报, 2010, 42(2): 256–261.
ZHAO Guozhu, WEI Minxiang, YANG Zhenglin. Modeling and simulation of regenerative braking of electric bus in antilock braking system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(2): 256–261. (in Chinese) |
| [9] | Ehsani M. Gao Y M, Gay S. Characterization of electric motor drives for traction applications[C]//Proceedings of the 29th Annual Conference of the IEEE Industrial Electronics Socety, November 2-6, 2003, Roanoke, Virginia, USA.Piscataway:IEEE Press, 2003, 1:891-896. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1280101 |
| [10] |
胡庆波, 郑继文, 吕征宇.
混合动力中无刷直流电机反接制动PWM调制方式的研究[J]. 中国电机工程学报, 2007, 27(30): 87–91.
HU Qingbo, ZHENG Jiwen, LÜ Zhengyu. Study on PWM strategy for braking of brushless DC motor in hybrid electric vehicle[J]. Proceedings of the Chinese Society Electrical Engineering, 2007, 27(30): 87–91. DOI:10.3321/j.issn:0258-8013.2007.30.016 (in Chinese) |
| [11] |
黄斐梨, 王耀明, 姜新建, 等.
电动汽车永磁无刷直流电机驱动系统低速能量回馈制动的研究[J]. 电工技术学报, 1995(3): 28–31, 36.
HUANG Feili, WANG Yaoming, JIANG Xinjian, et al. Study on regenerative braking of permanent magnet brushless DC motor drive system at Low speed for electric vehieles[J]. Transactions of China Electrotechnical Society, 1995(3): 28–31, 36. (in Chinese) |
| [12] | Unsal C, Kachroo P. Sliding mode measurement feedback control for antilock braking systems[J]. IEEE Transactions on Control Systems Technology, 1999, 7(2): 271–281. DOI:10.1109/87.748153 |
| [13] | Slotine J E, Li W. 应用非线性控制[M]. 程代展, 译. 北京: 机械工业出版社, 2006. |
| [14] | Chan C C, Chau K T, Jiang J Z, et al. Novel permanent magnet motor drives for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 1996, 43(2): 331–339. DOI:10.1109/41.491357 |
| [15] | 王兆安, 黄俊. 电力电子技术[M]. 3版. 北京: 机械工业出版社, 2008: 162-163. |
| [16] | Valeriote E M, Chang T G, Joehim D M. Fast charging of lead-acid batteries[C]//Proceedings of 9th Annual Battery Conference on Applications and Advances, January, 11-13, 1994, Long Beach, CA, USA.Piscataway:IEEE Press, 1994:33-38. https://www.infona.pl/resource/bwmeta1.element.ieee-art-000000283622 |
 2014, Vol. 37
2014, Vol. 37


