近年来,随着半导体制造工艺的进步和电力电子系统应用要求的提高,逆变器中IGBT模块的功率等级和密度也越来越高,迫使其内部的功率器件承受很高的热应力,尤其是对诸如风力发电、电力牵引和航空航天动力系统等工作环境恶劣且输出功率波动剧烈的应用场合,IGBT模块的寿命和长期可靠性受到了显著影响。工业界的调查反馈显示,34%的变换器系统故障原因可归咎于功率模块的损坏[1-2],IGBT模块作为众多类型功率半导体模块中应用最广泛、最成熟的一种,针对其故障机理的研究表明,与结温(Tj)相关的热循环过程和模块封装材料热膨胀系数不一致是主要诱因[3]。结温不仅同IGBT模块的寿命及可靠性直接相关,还会影响其工作性能,甚至于改变变换器输出端波形的谐波分布情况[4]。因此,获得既定工作条件下IGBT模块内功率器件的结温状况,对于确保其安全可靠的使用和冷却装置的合理选择等具有显著意义。
目前IGBT模块的结温已经可以通过实验方法获得[5-7],但其前提是针对特定的未塑封的IGBT模块,同时测温设备高昂的价格、苛刻的实验条件,以及实验过程中结温过高可能导致的器件损伤等因素都限制了其适用范围。因此,通过仿真评估功率器件在不同工作方式下的最高结温和波动范围,就成为保证系统和器件安全可靠、优化使用的一种有效手段[4-6, 8-15]。文献[4, 8-9]利用Saber软件里带热端口的IGBT器件物理模型来精确仿真器件瞬时结温的变化情况,文献[10]在ANSYS软件中建立起了IGBT模块封装的三维有限元模型,以此来仿真IGBT模块的三维热分布,这2种方法都存在建模过程复杂、建模参数难以获得和系统级仿真时间冗长以及仿真过程数据存储量巨大的缺点,其应用范围受到限制;文献[5-6, 11-12]基于查表法建立了IGBT模块的结温仿真模型,但其必须通过大量实验测量或者器件模型多次仿真模拟才能获得,工作量大;文献[13]利用几何方法得到了器件损耗的近似计算公式,然后结合模块封装结构的热网络模型来仿真IGBT模块的结温,由于其未考虑结温对损耗的影响,造成了一定的误差;此外,一些器件制造商所开发的针对本公司IGBT模块的产品选型软件[4, 14-15]也可以仿真获得模块内部器件芯片的结温,但是这类软件只针对有限的电路拓扑形式,拓展性和通用性差,仿真过程同样忽略了结温对器件损耗的反馈,且所获得的结温只是使用过程中的极限情况。
针对三相逆变器中IGBT模块的工作情况,推导建立了基于数学方法的IGBT模块损耗模型,同时考虑了电压、电流、栅极电阻以及结温等因素的影响,利用Foster热网络模拟模块由结到壳的瞬态热阻,基于此在MATLAB/Simulink中建立了简单实用的三相逆变器中IGBT模块结温仿真评估模型,并融入了热电耦合的因素,可以模拟不同负载工况下的模块结温,该模型原理简单,通用性好,可以为IGBT模块的可靠性评估、结温控制以及逆变器的热设计等服务。
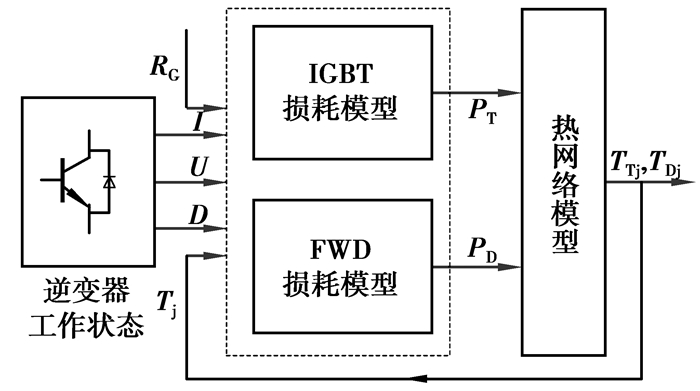
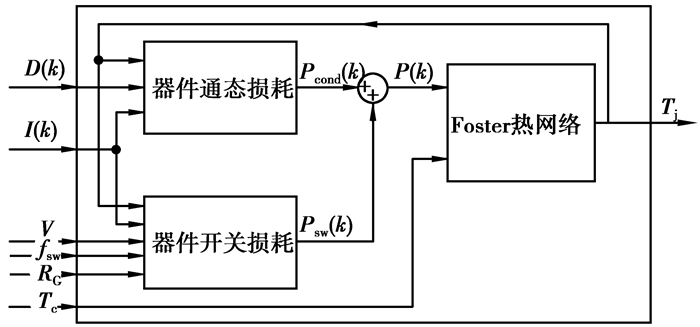
1 逆变器中IGBT模块结温仿真建模图 1所示为逆变器中IGBT模块(通常包括IGBT器件和反并联二极管FWD(free wheeling diode))结温仿真评估模型的结构框图。通过三相逆变器模型仿真过程中的各个工作状态,即流经器件的电流I,器件的端电压V和其导通占空比D等以及芯片的当前结温Tj,代入损耗模型获得器件在各个开关周期的损耗,通过利用热网络模型结温对损耗模型的反馈实现热电耦合,可以更真实的仿真模拟器件芯片结温的变化情况。
|
图 1 逆变器结温仿真评估模型结构框图 |
逆变器中IGBT模块的损耗模型是结温仿真建模过程中关键的一步。充分利用半导体器件制造商产品数据手册中的信息,即I-V曲线,E-I曲线以及E-RG曲线等,基于曲线拟合和插值等数学方法,计算得到损耗与电流、电压、结温等变量成函数关系的估算公式,并在MATLAB/Simulink中用数学运算模块构建出来,可以根据逆变器模型仿真过程中采样获得的电气参数与实时器件芯片结温,实时估算当前状态下的逆变器中IGBT模块的损耗。
热网络模型描述IGBT模块封装的动态热效应,其内部热阻、热容参数的组合用于模拟模块由结到壳的瞬态热阻曲线。其仿真进程与逆变器模型同步进行,根据实时计算得到的器件损耗状态以及当前模块的壳温Tc,可以快速仿真获得各功率器件芯片(IGBT/FWD)的结温变化,并立即反馈给器件损耗模型,及时更新下一仿真时刻器件损耗的计算结果,从而实现热电耦合仿真。
2 逆变器中IGBT模块功率损耗模型 2.1 IGBT模块功率损耗构成IGBT模块硬开关工作状态下的功率损耗主要有以下2个部分[16-18]:IGBT损耗PTtot,一般包括通态损耗PTcond、开通损耗Pon、关断损耗Poff,其中开通损耗和关断损耗合称开关损耗Psw;FWD损耗PDtot,一般包括通态损耗PDcond,反向恢复损耗Prr。且分别可以表示为
| $ {P_{{\rm{Ttot}}}} = {P_{{\rm{Tcond}}}} + {P_{{\rm{on}}}} + {P_{{\rm{off}}}} = {P_{{\rm{Tcond}}}} + {P_{{\rm{sw}}}}; $ | (1) |
| $ {P_{{\rm{Dtot}}}} = {P_{{\rm{Dcon}}}} + {P_{{\rm{rr}}}}。$ | (2) |
由于IGBT内部通态电阻和PN结电位的影响,在导通状态下IGBT会保持一定的饱和压降Vce(sat),并与通态电流IC共同作用产生了通态损耗。其表达式如下
| $ \begin{array}{*{20}{c}} {{V_{{\rm{ce}}\left( {{\rm{sat}}} \right)}} = {k_{{\rm{TR}}}}\left( {{T_{{\rm{Tj}}}}} \right) \cdot {R_{{\rm{ce,2}}{{\rm{5}}^ \circ }{\rm{C}}}} \cdot {I_{\rm{C}}} + }\\ {{k_{{\rm{TV}}}}\left( {{T_{{\rm{Tj}}}}} \right) \cdot {V_{{\rm{ceo,2}}{{\rm{5}}^ \circ }{\rm{C}}}},} \end{array} $ | (3) |
| $ {P_{{\rm{Tcond}}}}{\rm{ = }}{V_{{\rm{ce}}\left( {{\rm{sat}}} \right)}} \cdot {I_{\rm{C}}} \cdot {D_{\rm{T}}} = f\left( {{I_{\rm{C}}},{T_{{\rm{Tj}}}},{D_{\rm{T}}}} \right), $ | (4) |
式中:Rce,25 ℃和Vceo,25 ℃分别为IGBT在结温25 ℃时的额定通态电阻和压降;TTj为IGBT的实际结温;kTR(TTj)和kTV(TTj)分别为IGBT的通态电阻和压降的温度相关项;DT为IGBT工作状态的导通占空比。
2.1.2 IGBT开关损耗IGBT在硬开关模式下工作时,开通和关断过程中其电压、电流波形会有重叠,因而产生了一定的开关损耗,考虑对器件开关损耗影响显著的主要因素,如集电极电流IC、集-射极电压VCE、栅极电阻RG、结温TTj以及开关频率fsw,并结合产品数据手册中的Eon、Eoff曲线,IGBT的开通、关断能量和开关损耗可以分别表示为
| $ \begin{array}{*{20}{c}} {{E_{{\rm{on}}}} = \left( {{a_{{\rm{on}}}}I_{\rm{C}}^2 + {b_{{\rm{on}}}}{I_{\rm{C}}} + c} \right) \cdot \frac{{{V_{{\rm{C}}{\rm{E}}}}}}{{{V_{{\rm{rated}}}}}} \cdot }\\ {{k_{{\rm{on}}}}\left( {{T_{{\rm{Tj}}}}} \right) \cdot \frac{{{E_{{\rm{on}}}}\left( {{R_{\rm{G}}}} \right)}}{{{E_{{\rm{on}}}}\left( {{R_{{\rm{Grated}}}}} \right)}};} \end{array} $ | (5) |
| $ \begin{array}{*{20}{c}} {{E_{{\rm{off}}}} = \left( {{a_{{\rm{off}}}}I_{\rm{C}}^2 + {b_{{\rm{off}}}}{I_{\rm{C}}} + c} \right) \cdot \frac{{{V_{{\rm{C}}{\rm{E}}}}}}{{{V_{{\rm{rated}}}}}} \cdot }\\ {{k_{{\rm{off}}}}\left( {{T_{{\rm{Tj}}}}} \right) \cdot \frac{{{E_{{\rm{off}}}}\left( {{R_{\rm{G}}}} \right)}}{{{E_{{\rm{off}}}}\left( {{R_{{\rm{Grated}}}}} \right)}};} \end{array} $ | (6) |
| $ {P_{{\rm{sw}}}} = {f_{{\rm{sw}}}} \cdot {E_{{\rm{sw}}}} = {f_{{\rm{sw}}}} \cdot \left( {{E_{{\rm{on}}}} + {E_{{\rm{off}}}}} \right), $ | (7) |
式中:a、b、c是通过开通和关断损耗曲线拟合得到的常数;Vrated和RGrated分别为参考电压和参考栅极电阻;k(TTj)为损耗的温度相关项;RG和E(RG)分别为选用的栅极电阻和相对应的损耗。
2.1.3 FWD通态损耗同IGBT通态损耗的分析一样,FWD的通态压降和损耗表达式如下
| $ \begin{array}{*{20}{c}} {{V_{\rm{F}}} = {k_{{\rm{DR}}}}\left( {{T_{{\rm{Dj}}}}} \right) \cdot {R_{{\rm{F,2}}{{\rm{5}}^ \circ }{\rm{C}}}} \cdot {I_{\rm{F}}} + }\\ {{k_{{\rm{DV}}}}\left( {{T_{{\rm{Dj}}}}} \right) \cdot {V_{{\rm{FO,2}}{{\rm{5}}^ \circ }{\rm{C}}}};} \end{array} $ | (8) |
| $ {P_{{\rm{Dcond}}}} = {V_{\rm{F}}} \cdot {I_{\rm{D}}} \cdot {D_{\rm{D}}} = f\left( {{I_{\rm{D}}},{T_{{\rm{Dj}}}},{D_{\rm{D}}}} \right); $ | (9) |
式中:RF,25 ℃和VFO,25 ℃分别为FWD在结温25 ℃时的额定通态电阻和压降;TDj为FWD的实际结温;kDR(TDj)和kDV(TDj)分别为FWD的通态电阻和压降的温度相关项;DD为FWD工作状态的导通占空比。
2.1.4 FWD反向恢复损耗二极管关断时,其反向阻断能力的恢复需要经过一段时间,此过程中流经FWD的电流与其端电压有重叠,产生反向恢复损耗。其可以表示为
| $ \begin{array}{*{20}{c}} {{E_{{\rm{rr}}}} = \left( {{a_{{\rm{rr}}}}I_{\rm{D}}^2 + {b_{{\rm{rr}}}}{I_{\rm{D}}} + {c_{{\rm{rr}}}}} \right) \cdot \frac{{{V_{\rm{D}}}}}{{{V_{{\rm{Drated}}}}}} \cdot }\\ {{k_{{\rm{rr}}}}\left( {{T_{{\rm{Dj}}}}} \right) \cdot \frac{{{E_{{\rm{rr}}}}\left( {{R_{\rm{G}}}} \right)}}{{{E_{{\rm{rr}}}}\left( {{R_{{\rm{Grated}}}}} \right)}},} \end{array} $ | (10) |
| $ {P_{{\rm{rr}}}} = {f_{{\rm{sw}}}} \cdot {E_{{\rm{rr}}}}, $ | (11) |
式中:arr、brr、crr是通过FWD反向恢复损耗曲线拟合得到的常数;VDrated和RGrated分别为参考电压和参考栅极电阻;krr(TDj)为损耗的温度相关项;RG和E(RG)分别为选用的栅极电阻和相对应的损耗。
2.2 逆变器中IGBT模块功率损耗计算由于2电平逆变器结构的对称性,并且各相选用的IGBT模块特性往往相同,因此只需对1个IGBT模块进行损耗分析。
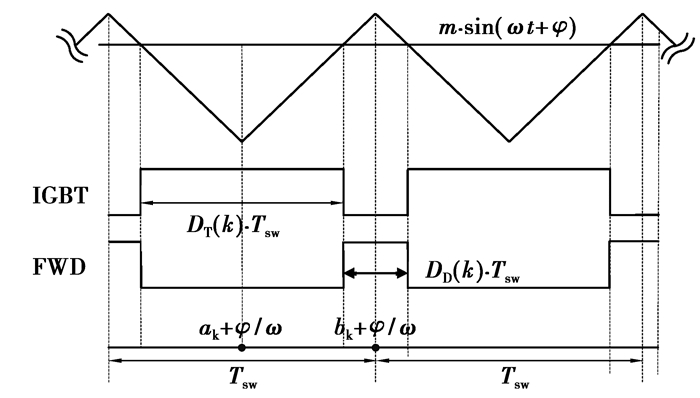
2.2.1 导通占空比的计算与电流采样在器件工作区域内,其导通状态不连续。双极性PWM调制模式下,每个载波周期内,器件的导通时间可由调制波与载波的比较获得,如图 2所示。
|
图 2 开关状态确定 |
设ak、bk分别为第k个载波周期的中心位置,当采用规则采样时,IGBT和FWD的第k个脉冲内的占空比表示如下[17-18]
| $ {D_{\rm{T}}}\left( k \right) = \frac{{1 + m \cdot \sin \left( {\omega \cdot {a_{\rm{k}}} + \varphi } \right)}}{2}; $ | (12) |
| $ {D_{\rm{D}}}\left( k \right) = \frac{{1 - m \cdot \sin \left( {\omega \cdot {b_{\rm{k}}} + \varphi } \right)}}{2}; $ | (13) |
忽略电流谐波,相电流可以表示为
| $ I = {I_M} \cdot \sin \left( {\omega t} \right)。$ | (14) |
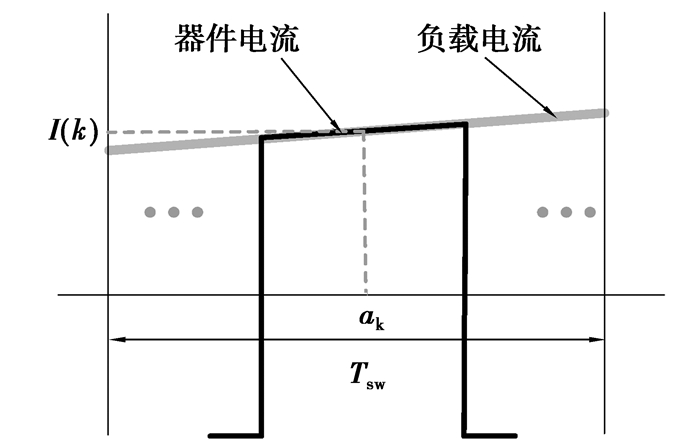
当开关周期Tsw足够小时,可以认为器件的通态电流和通态电压在Tsw内保持不变,如图 3所示,则第k个载波周期内,器件的通态电流可表示为
|
图 3 器件电流采样 |
| $ I\left( k \right) = {I_M} \cdot \sin \left( {\omega \cdot {a_k}} \right) = {I_M} \cdot \sin \left( {\frac{{\rm{ \mathit{ π} }}}{N} \cdot k} \right), $ | (15) |
其中N=Tc/Tsw为载波比,k=1,2…N,IM为流经器件的电流幅值。
2.2.2 损耗计算在一个调制周期内,随着开关状态的变化及考虑电压、电流的相位关系,各开关器件按一定规律轮流导通,在导通区段内器件根据调制波与载波的比较做相应的开、关动作,则在每个开关周期内,IGBT和FWD的损耗可以表示为
| $ {P_{\rm{T}}}\left( k \right) = {P_{{\rm{Tcond}}}}\left( k \right) + {f_{{\rm{sw}}}} \cdot \left( {{E_{{\rm{on}}}}\left( k \right) + {E_{{\rm{off}}}}\left( k \right)} \right); $ | (16) |
| $ {P_{\rm{D}}}\left( k \right) = {P_{{\rm{Dcond}}}}\left( k \right) + {f_{{\rm{sw}}}} \cdot {E_{{\rm{rr}}}}\left( k \right)。$ | (17) |
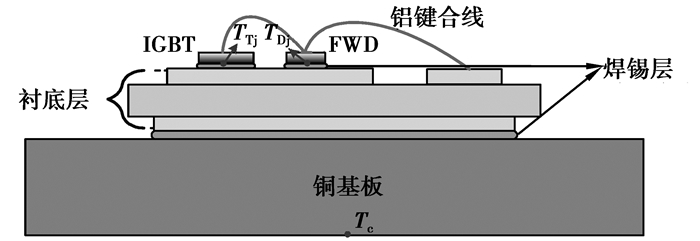
IGBT模块封装是一个由不同材料组成的“三明治”型多维结构,其横截面结构如图 4所示,其中IGBT器件和FWD的硅芯片通过锡焊层与绝缘衬底层连接,并固定在铜基板上,其工作过程中,各个硅芯片上的铝键合线负责导通电流。
|
图 4 IGBT模块结构截面图 |
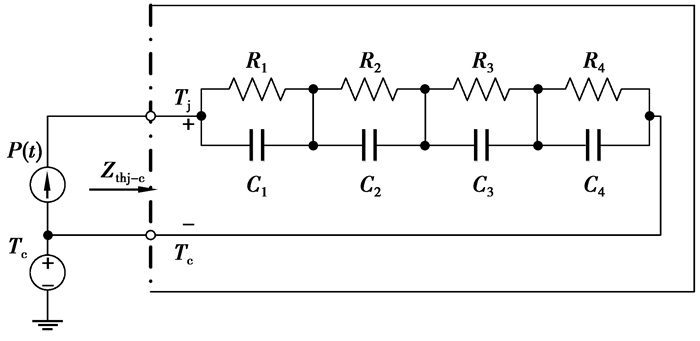
根据电-热比拟理论,通常采用集中等效的传热模型来模拟IGBT模块封装的热特性,图 5即为Foster型等效传热网络,这种简化的传热模型可以方便的以电路网络的形式在电路仿真器里实现。
|
图 5 半导体器件的等效传热网络 |
IGBT模块瞬态热阻Zthj-c(t)定义为热流通路上从芯片到外壳的温度差与通道上耗散功率之比,即
| $ {Z_{{\rm{thj}} - {\rm{c}}}}\left( t \right) = \frac{{{T_{\rm{j}}}\left( t \right) - {T_{\rm{c}}}\left( t \right)}}{P} = \frac{{\Delta {T_{{\rm{jc}}}}}}{P}。$ | (18) |
图 5中RC梯形网络是通过对仿真或实验测得的动态热阻抗曲线的指数级数拟合得到各阶RC环的热特性参数的,拟合函数式[19-20]为
| $ {Z_{{\rm{thj}} - {\rm{c}}}}\left( t \right) = \sum\limits_{i = 1}^4 {{R_i}\left( {1 - {{\rm{e}}^{\frac{{ - t}}{{{R_i}{C_i}}}}}} \right)} 。$ | (19) |
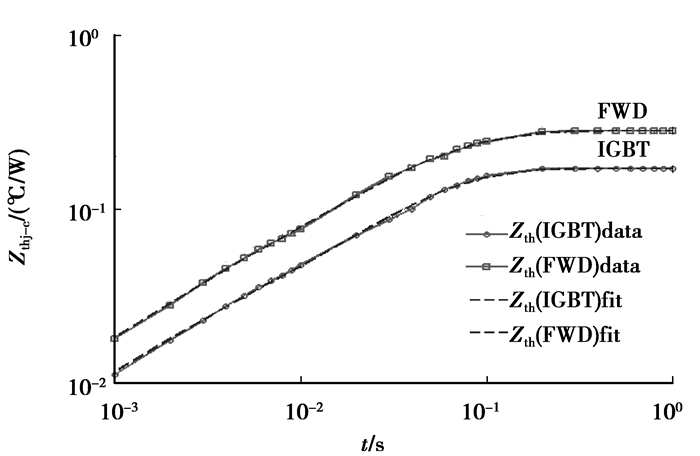
表 1中给出了富士电机2MBI150U4H-170型号IGBT模块相应的Ri和Ci值,如图 6所示。
| 表 1 IGBT模块传热模型的参数 |
|
图 6 富士电机2MBI150U4H-170型IGBT模块的瞬态热响应曲线[21] |
从图 6可以看出,利用MATLAB拟合工具箱拟合获得的Zthj-c(t)热响应曲线同器件产品数据手册提供的曲线吻合很好。
4 仿真与计算 4.1 电热仿真模型实现与验证利用分析得到的逆变器中IGBT模块损耗模型和热网络模型,基于MATLAB/Simulink,建立了三相逆变器中IGBT模块的结温仿真模型,能够实时输出功率器件结温,可以方便地评估不同负载工况对IGBT模块工作结温的影响,其原理框图如图 7所示。
|
图 7 器件结温仿真模型原理框图 |
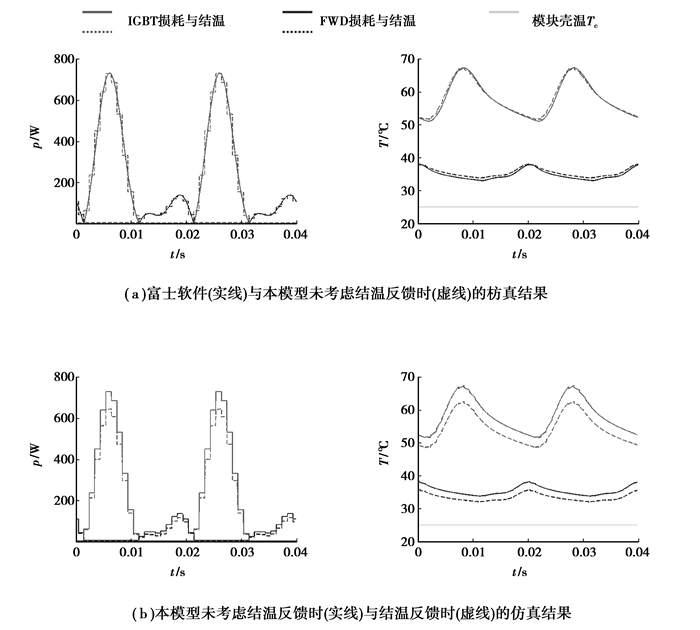
采用本模型,针对富士电机2MBI150U4H-170型IGBT模块进行了仿真,并同富士电机官方分析软件Fuji IGBT simulator ver.5.1的仿真结果进行了对比[4, 14-15],仿真参数设置如下:2电平三相逆变器,SPWM调制算例,直流电压900 V,工作电流150 A,额定功率因数0.9,调制度1,基波频率50 Hz,开关频率1 KHz。设定IGBT模块壳温为25 ℃。表 2给出了损耗模型的参数,图 8为仿真对比。
| 表 2 IGBT模块损耗模型的参数 |
|
图 8 功率损耗和结温变化对比 |
图 8给出了富士公司仿真器和本文模型的仿真结果对比,仿真结果显示,富士软件的计算没有考虑结温的反馈耦合,其结果只是一种极限情况,目的是使用户在产品选型阶段避免模块超额,从图 8(a)可以看出,本模型可以合理的满足工程设计需要。此外,本模型可以将结温同损耗模型耦合起来,从而能够更加真实的反映IGBT和FWD的结温变化(图 8(b)),为IGBT模块的可靠性评估服务。
4.2 仿真结果分析下面利用本模型分析不同负载工况对IGBT模块结温的影响,此时考虑结温反馈。
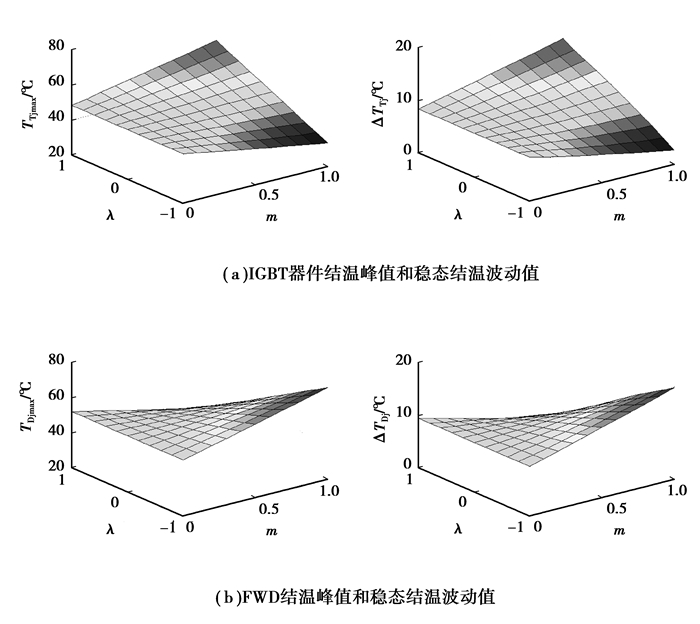
4.2.1 功率因数(和调制度m对结温的影响)图 9给出了IGBT和FWD的Tjmax和ΔTj与功率因数λ (cos φ)和调制度m的关系图形。
|
图 9 功率因数λ和调制度m对结温的影响 |
由图可以看出,当调制度m≠0时,IGBT的结温峰值和稳态波动值都随着功率因数λ的增大而增大,FWD的情况则正好相反;当调制度m=0时,IGBT和FWD的结温都固定不变。在功率因数λ>0时,随着调制度的增加,IGBT的结温峰值和稳态波动值相应的近似线性增加,FWD的情况正好与此相反;功率因数λ=0时,IGBT和FWD的结温无变化;功率因数λ<0时的情况同λ>0相反。究其根源,功率因数λ和调制度m影响占空比,从而影响到IGBT和FWD的通态损耗,导致其发热情况相应的发生变化。
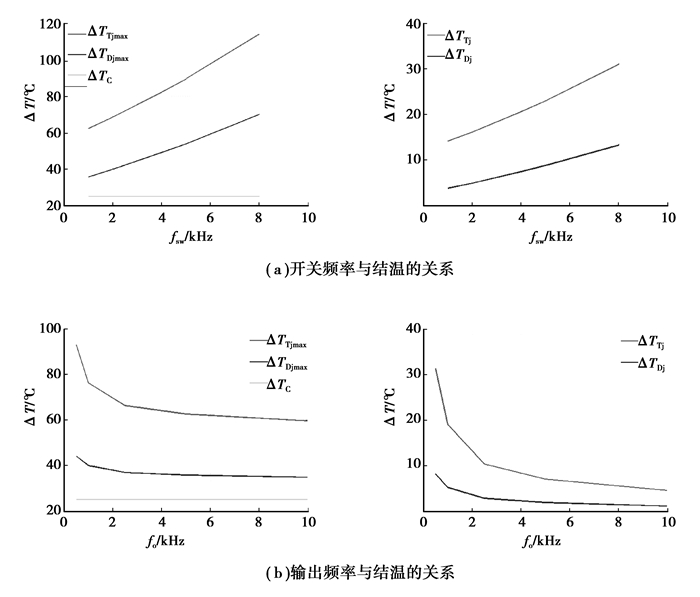
4.2.2 工作频率对结温的影响如图 10(a)所示,随着开关频率的增加,IGBT和FWD的结温峰值和稳态波动值都显著提升;结温波动值与峰值也会随着输出频率的不同而有所差异,如图 10(b)所示,低频输出时,结温波动幅度较剧烈,其峰值也较高。此时,功率器件承受热应力较大,长期在此状态下工作会影响到其可靠性。
|
图 10 工作频率对结温的影响 |
针对三相PWM逆变器中IGBT模块的结温仿真模型进行了研究。推导得到的IGBT模块损耗模型,综合考虑了电流、电压、栅极电阻以及结温的影响,并且建模所需参数容易获得,因而具有很强的实用价值;然后分析了模块封装的集中等效传热模型,基于曲线拟合提取到了Foster网络参数,简单可行。根据以上模型在MATLAB/Simulink中搭建了2电平三相逆变器中IGBT模块的结温仿真模型,可应用于逆变器的热设计和降损设计,对于延长IGBT模块的寿命和提高其应用可靠性也有重要意义。所得结论如下
1) 所述模型与器件的具体类型无关,可以扩展到MOSFET、IPM等功率模块,也同样适用于BUCK、BOOST、单相桥式电路等变换器,参数提取简单,仿真结果可以满足工程设计的要求,具有很好的通用性和实用性。
2) 调制度m、功率因数(以及工作频率fsw和fo的变化都会导致IGBT模块内功率器件芯片的结温发生变化,在逆变器实际运行中,合理的调控这些因素,可以实现结温控制。
3) 为了研究方便,结温仿真模型建立在IGBT模块壳温固定在25 ℃的基础上,如何考虑实际应用中壳温的变化情况以提高结温模拟的真实性,以及寻求进一步优化损耗模型的精度,都有待进行更深入的研究。
| [1] | Yang S Y, Xiang D W, Bryant A, et al. Condition monitoring for device reliability in power electronic converters-A review[J]. IEEE Trans on Power Electronics, 2010, 25(11): 2734–2752. DOI:10.1109/TPEL.2010.2049377 |
| [2] | Yang S, Bryant A T, Mawby P A, et al.An industry-based survey of reliability in power electronic converters[C].ECCE Conf. Rec., San Jose, September, 2009. http://ieeexplore.ieee.org/document/5729810/ |
| [3] | Mauro C. Selected failure mechanisms of modern power modules[J]. Microelectronics Reliability, 2002, 42: 653–667. DOI:10.1016/S0026-2714(02)00042-2 |
| [4] | Xiang D W, Yang S Y, Li R, et al.Change of terminal characteristics of a voltage-source-inverter (VSI) due to semiconductor device degradation[C].13th European conference on Power Electronics and Applications(EPE'09), Barcelona, 2009. http://ieeexplore.ieee.org/document/5279301/ |
| [5] | Khatir Z B, Carubelli S, Frederic L. Real-time computation of thermal constraints in multichip power electronic devices[J]. IEEE Trans on Components and Packaging Technologies, 2004, 27(2): 337–344. DOI:10.1109/TCAPT.2004.828563 |
| [6] | Mahera M, Mark Johnson C. Real-time compact thermal models for health management of power electronics[J]. IEEE Trans on Power Electronics, 2010, 25(6): 1416–1425. DOI:10.1109/TPEL.2010.2040634 |
| [7] | Commission Electrotechnique International. Semi-conductor devices-Discrete devices-Part 9:Insulated-gate bipolar transistors (IGBTs)[S].GENEVA, SWITZERLAND:IEC Central Office, 2001. |
| [8] | Reichl J V.Inverter Dynamic electro-thermal simulation with experiment verification[D].Virginia, Virginia Polytechnic Institute and State University, 2005. http://www.openthesis.org/documents/Inverter-Dynamic-Electro-Thermal-Simulation-587974.html |
| [9] | Alan Mantooth H, Allen R Hefner J r. Electrothermal simulation of an IGBT PWM inverter[J]. IEEE Trans on Power Electronics, 1997, 12(3): 474–484. DOI:10.1109/63.575675 |
| [10] | Yun C S, Reglil P, Waldmeyer J, et al.Static and dynamic thermal characteristics of IGBT power modules[C].The 11th International Symposium on Power Semiconductor Devices and ICs (ISPSD'99), Toronto, Canada, 1999. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=764037 |
| [11] | Zhou Z, Khanniche M S, Igic P, et al. A fast power loss calculation method for long real time thermal simulation of IGBT modules for a three-phase inverter system[C].2005 European Conference on Power Electronic and Applications, Dresden, Germany, 2005. http://ieeexplore.ieee.org/document/1665788/ |
| [12] | Bryant A T, Mawby P A, Palmer P P, et al. Exploration of power device reliability using compact device models and fast electrothermal simulation[J]. IEEE Trans on Industry Applications, 2008, 44(3): 894–903. DOI:10.1109/TIA.2008.921388 |
| [13] | Rajapakse A D, Gole A M, Wilson P L. Electromagnetic transients simulation models for accurate representation of switching losses and thermal performance in power electronic systems[J]. IEEE Trans on Power Delivery, 2005, 20(1): 319–327. DOI:10.1109/TPWRD.2004.839726 |
| [14] | Fuji IGBT simulator ver.5.1, https://www.fujielectric.co.jp/contact_1/semi_chi_01_01.html. |
| [15] |
黄碧霞, 陈阳生.
一种三相逆变器损耗分析方法[J]. 微电机, 2009, 42(9): 49–52.
HUANG Bixia, CHEN Yangsheng. Prediction of power losses in three-phase inverter based on system simulation[J]. Micromotor, 2009, 42(9): 49–52. (in Chinese) |
| [16] |
熊妍, 沈燕群, 江剑, 等.
IGBT损耗计算和损耗模型研究[J]. 电源技术应用, 2005, 25(1): 31–33.
XIONG Yan, SHEN Yanqun, JIANG Jian, et al. Study on loss calculation and Model for IGBT[J]. Power Supply Technologies and Applications, 2005, 25(1): 31–33. (in Chinese) |
| [17] |
潘武略, 徐政, 张静, 等.
电压源换流器型直流输电换流器损耗分析[J]. 中国电机工程学报, 2008, 28(21): 7–14.
PAN Wulue, XU Zheng, ZHANG Jing, et al. Dissipation analysis of VSC-HVDC converter[J]. Proceedings of the CSEE, 2008, 28(21): 7–14. (in Chinese) |
| [18] |
胡建辉, 李锦庚, 邹继斌, 等.
变频器中的IGBT模块损耗计算及散热系统设计[J]. 电工技术学报, 2009, 24(3): 159–163.
HU Jianhui, LI Jingeng, ZOU Jibin, et al. Losses calculation of IGBT module and heat dissipation system design of inverters[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 159–163. (in Chinese) |
| [19] | Luo Z H, Ahn H Y, Mahmoud A. A thermal model for insulated gate bipolar transistor module[J]. IEEE Trans on Power Electronics, 2004, 19(4): 902–907. DOI:10.1109/TPEL.2004.830089 |
| [20] |
陈明, 胡安, 唐勇, 等.
绝缘栅双极型晶体管传热模型建模分析[J]. 高电压技术, 2011, 37(2): 453–459.
CHEN Ming, HU An, TANG Yong, et al. Modeling analysis of IGBT thermal model[J]. High Voltage Engineering, 2011, 37(2): 453–459. (in Chinese) |
| [21] | Fuji Semiconductor GmbH.2MBI150U4H-170 product specification datasheet[R].Japan, 2008. |
 2014, Vol. 37
2014, Vol. 37


