超声波电机是近些年发展起来的一种利用压电陶瓷逆压电效应的新型电机。超声电机运行包含诸如压电能量转换、摩擦能量传递等非线性过程,其也被认为是一种非线性、时变和强耦合的被控对象[1],对超声波电机本体模型的研究具有重要意义。
最早对超声电机定、转子接触模型进行定量分析的是上羽贞行和黑泽实[2]。1995年J Maas等[3]对超声电机赫兹理论模型做了详细的研究与分析,提出赫兹理论模型下压力分布函数的边界条件,但没有对驱动区间和制动区间的关系做深入的讨论。文献[4]设计了一种微小旋转型超声电机并建立了其瞬态过程的动力学方程,分析了瞬态特性。文献[5]将空间域分析与预压力结合在一起讨论了预压力对超声电机输出性能的影响。文献[6]建立了旋转行波超声电机的多变量非线性Hammerstein模型,并分析证明了采用两步法广义预测控制策略的可行性。文献[7]的研究重点在超声电机数学模型,分析了预压力对电机机械性能的影响。但相关文献并没有针对超声电机数学模型本身所体现出来的不稳定性进行讨论[8-15]。
文章是在行波型超声波电机的赫兹数学模型基础上,基于李雅普诺夫平衡条件,对行波型超声波电机的稳定性开展研究,针对定转子接触模型空间域的3种情况进行讨论,并结合预压力、负载转矩和速度3者之间的关系对超声波电机的稳定运行进行定性分析,研究成果有助于为超声波电机的设计和控制提供借鉴。
1 行波型超声电机定转子接触模型超声波电机的运行是通过定转子之间的摩擦来传递动力,1882年物理学家赫兹研究的两圆柱体接触面的应力、应变场、位移场的分布情况及特点[16],为超声波电机定转子的接触模型发展奠定了基础。
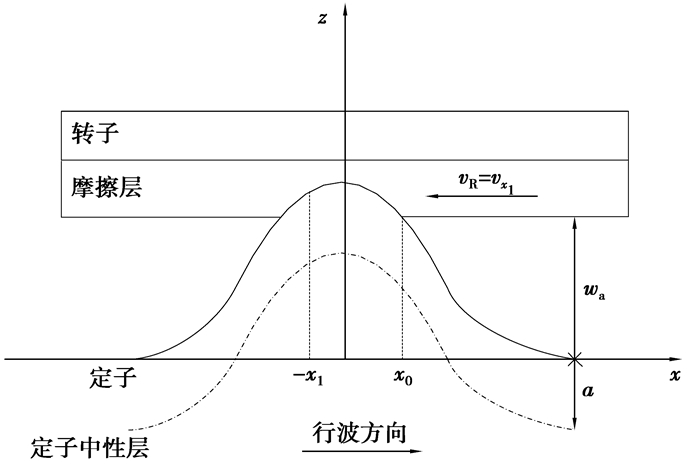
尽管超声波电机定、转子的接触模型与一般的赫兹接触模型不完全相同,但赫兹接触理论能较好地解决超声电机定、转子接触模型中遇到的问题。根据电机实际运行的情况,假设定、转子在运行的过程中均不产生接触形变,只有摩擦材料层产生形变,定、转子表面不完全紧密结合且无相对滑动。简化出刚性定子和弹性转子接触模型,图 1为刚性定子和弹性转子的接触摩擦机理图[1]。
|
图 1 刚性定子和弹性转子的接触摩擦机理图 |
根据行波超声电机的理论[3],定子上的行波是由分别作用在A、B两相上的驻波叠加而来,行波的波动过程为
| $ w\left( x \right) = {w_{\rm{A}}} \cdot \cos \left( {kx} \right), $ | (1) |
| $ {v_{\rm h}}\left( x \right) = - k{w_{\rm{A}}}a\omega \cdot \cos \left( {kx} \right), $ | (2) |
式中:w(x)为定子表面质点的纵向振动位移;vh(x)定子表面质点的切向速度;wA为A、B两相上施加信号的振幅。
根据赫兹接触模型理论转子的转速为
| $ {v_{\rm{R}}} = {\omega _{\rm{R}}} \cdot R = k{w_{\rm{A}}}a\omega \cos \left( {k{x_1}} \right)。$ | (3) |
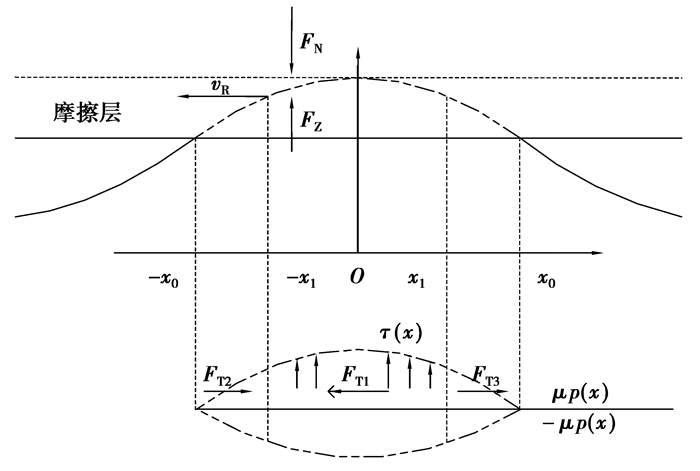
图 2为摩擦力、压力分布图,vR为转子转速,x1在定子坐标系(x,z)上为定子和转子的等速点,vh=vR,x0为定子和转子接触的临界点。所以定、转子在(x,z)中的接触区间可以划分为3个部分,(-x1,x1)区间内vh>vR为驱动区间,定子在这段区间内给转子提供驱动力FT1。(-x0,-x1)和(x1,x0)区间内vh<vR为制动区间,存在反向阻力FT2和FT3。
|
图 2 摩擦力、压力分布图 |
图 2中压力分布为
| $ \tau \left( x \right) = {\mathop{\rm sgn}} \left( {\left| {{v_{\rm{h}}}\left( x \right)} \right| - \left| {{v_{\rm{R}}}} \right|} \right) \cdot \mu p\left( x \right), $ | (4) |
| $ p\left( x \right) = {C_{\rm{N}}} \cdot {w_{\rm{A}}}\left( {\cos kx - \cos k{x_0}} \right), $ | (5) |
式中:p(x)为压力分布函数;CN为CN=Eb/hr;E为定子金属弹性材料的杨氏模量;b为摩擦层接触面的宽度;w为定子振动幅值;hr为摩擦层的厚度。
转子受到的作用力为
| $ {F_{\rm{T}}} = {F_{{\rm{T1}}}} - {F_{{\rm{T2}}}} - {F_{{\rm{T3}}}} = \int_{ - x}^x {\tau \left( x \right){\rm{d}}x} , $ | (6) |
定子波峰对转子的轴向压力为
| $ \begin{array}{*{20}{c}} {{F_z} = n\int_{ - x}^x {p\left( x \right){\rm{d}}x} = }\\ {2{C_{\rm{N}}}n{w_{\rm{A}}}\left( {\frac{1}{k}\sin kx - x\cos kx} \right)。} \end{array} $ | (7) |
行波型超声电机转子的运动主要分为轴向和周向,轴向主要是预压力和定子对转子轴向的作用力,周向主要是驱动力、摩擦阻力和负载的作用,可以分别表示为
| $ {m_{\rm{R}}}{{w''}_{\rm{A}}} + {d_{\rm{z}}}{{w'}_{\rm{A}}} = {F_{\rm{Z}}} - {F_{\rm{N}}}, $ | (8) |
| $ J{{\omega '}_{\rm{R}}} + {D_{\rm{R}}}{\omega _{\rm{R}}} = n{F_{\rm{T}}}R - {M_{\rm{L}}}。$ | (9) |
文献[3]针对行波型超声波电机引入了超声波电机制动区间和驱动区间相对位置的讨论,但并没有对区间的变换交替所引起的行波型超声波电机的稳定性进行研究分析。根据李雅普诺夫对平衡状态的判定[17],对于时间t,如果满足
| $ x' = f\left( {x,t} \right) = 0, $ |
该状态x称为平衡状态。平衡状态的各分量相对于时间不再发生变化。若已知状态方程,令x′=0所求得的解x,便是一种平衡状态。
线性定常系统x′=Ax,其平衡状态满足Ax=0,当A为非奇异矩阵时,系统只有唯一的解,只存在一个平衡状态,若A为奇异矩阵,系统则存在无穷多个平衡状态。式(9)可以看作是李雅普诺夫对平衡状态的定义在超声波电机上的直接应用。
2.1 超声电机运行区间1) 当x0>x1时
| $ \begin{array}{*{20}{c}} {{F_{\rm{T}}} = 2\int_0^{{x_0}} {{\mathop{\rm sgn}} \left( {\left| {{v_{\rm{h}}}\left( x \right)} \right| - \left| {{v_{\rm{R}}}} \right|} \right) \cdot \mu p\left( x \right)} = }\\ {2\mu \left[ {\int_0^{{x_1}} {p\left( x \right){\rm{d}}x} - \int_{{x_1}}^{{x_0}} {p\left( x \right){\rm{d}}x} } \right] = }\\ {2\mu {C_{\rm{N}}}{w_{\rm{A}}}\left[ {2\left( {\frac{1}{k}\sin k{x_1} - {x_1}\cos k{x_0}} \right) - } \right.}\\ {\left. {\left( {\frac{1}{k}\sin k{x_0} - {x_0}\cos k{x_0}} \right)} \right],} \end{array} $ | (10) |
此时的李雅普诺夫平衡方程为
| $ \begin{array}{*{20}{c}} {2\left( {\frac{1}{k}\sin k{x_1} - {x_1}\cos k{x_0}} \right) - }\\ {\left( {\frac{1}{k}\sin k{x_0} - {x_0}\cos k{x_0}} \right) - }\\ {\frac{{{D_{\rm{R}}}ka{W_{\rm{A}}}\omega }}{{2\mu {C_{\rm{N}}}{W_{\rm{A}}}n{R^2}}} \cdot \cos k{x_1} = \frac{{{M_{\rm{L}}}}}{{2\mu {C_{\rm{N}}}{W_{\rm{A}}}nR}}。} \end{array} $ | (11) |
在式(11)中,如果负载ML、接触层的等效弹性系数CN、定子振幅WA、振动模态阶数n和有效接触半径R为已知的情况下,就可以得到李雅普诺夫稳定情况下x0和x1的关系。
2) 当x0<x1时
此时的压力分布函数为
| $ p\left( x \right) = {C_{\rm{N}}} \cdot {w_{\rm{A}}}\left( {\cos kx - \cos k{x_1}} \right), $ | (12) |
转子受到的作用力为
| $ \begin{array}{*{20}{c}} {{F_{\rm{T}}} = {F_{{\rm{T1}}}} - {F_{{\rm{T2}}}} - {F_{{\rm{T3}}}} = }\\ {2\mu \left[ {\int_{{x_0}}^{{x_1}} {p\left( x \right){\rm{d}}x} - \int_0^{{x_0}} {p\left( x \right){\rm{d}}x} } \right],} \end{array} $ | (13) |
化解后的作用力为
| $ \begin{array}{*{20}{c}} {{F_{\rm{T}}} = 2\mu {C_{\rm{N}}}{w_{\rm{A}}}\left[ {\left( {\frac{1}{k}\sin k{x_1} - {x_1}\cos k{x_1}} \right) - } \right.}\\ {\left. {2\left( {\frac{1}{k}\sin k{x_0} - {x_0}\cos k{x_1}} \right)} \right]。} \end{array} $ | (14) |
对比当x0>x1和x0<x1时的作用力FT可以得到
| $ {F_{\rm{T}}}\left( {{x_0} < {x_1}} \right) = - {F_{\rm{T}}}\left( {{x_0} > {x_1}} \right), $ |
表明,当分别满足x0>x1和x0<x1 2种情况下的x0和x1对等时,所求得的作用力在数值相等符号相反,并且上式成立的前提条件是在定转子接触的区间内依然存在一点x1使得转子的转速与定子表面切向分量的转速相等,从式(3)可以看到转子转速的表达式是一个余弦函数,即当x0<x1时:
| $ k\mathit{\boldsymbol{A}}a\omega \cos \left( {k{x_0}} \right) > k\mathit{\boldsymbol{A}}a\omega \cos \left( {k{x_1}} \right)。$ |
根据x0和x1物理意义上划分x0为制动区间x1为驱动区间,认为制动区间的转速是小于驱动区间的,即
| $ k\mathit{\boldsymbol{A}}a\omega \cos \left( {k{x_0}} \right) < k\mathit{\boldsymbol{A}}a\omega \cos \left( {k{x_1}} \right), $ |
由此可以认定行波型超声电机在稳定运行时不会出现x0<x1的情况。
3) 当x0=x1时
此时转子受到的作用力为
| $ \begin{array}{*{20}{c}} {{F_{\rm{T}}} = 2\mu \int_0^{{x_1}} {p\left( x \right){\rm{d}}x} = }\\ {2\mu {C_{\rm{N}}}{w_{\rm{A}}}\left( {\frac{1}{k}\sin k{x_0} - {x_0}\cos k{x_0}} \right)。} \end{array} $ | (15) |
此时,在整个[0,x0]区间内摩擦力提供转子驱动力,转子的速度与定子切线速度在x0=x1出相等,即vR=vh(x0)。因为此时认定摩擦力没有阻碍作用,所以,此时的定转子能量的传递效率最高,定子传递给转子的能量将用在克服转子轴向阻尼损耗DRωR和提供给负载ML上。
根据式(3)、(6)和(9)可以得
| $ \begin{array}{*{20}{c}} {{M_{\rm{L}}} = nR \cdot 2\mu {C_{\rm{N}}}{w_{\rm{A}}}\left\{ {\frac{1}{k}\sin \left[ {\arccos \left( {{\omega _R} \cdot \frac{R}{{k{w_{\rm{A}}}\omega a}}} \right)} \right] - } \right.}\\ {\left. {{\omega _R} \cdot \frac{R}{{k{w_{\rm{A}}}\omega a}} \cdot \arccos \left( {{\omega _R} \cdot \frac{R}{{k{w_{\rm{A}}}\omega a}}} \right)} \right\} - {D_R}{\omega _R}。} \end{array} $ | (16) |
在理论上是存在x0=x1这一点,且x0的值由预压力FN确定,此时因为x1=x0,角速度ωR和驱动力FT可以确定,再根据式(9)可以确定超声电机在运行时转子轴向上的阻尼损耗和对应的负载输出,即一个预压力对应一个转速和负载输出。由式(3)可以知道x1的最大驱动区间为λ/4,当速度为λ/4时所对应的速度为0,可以得到x1=λ/4为定子驱动转子驱动区间的极限状态。
从式(9)中可以看到转子的轴向阻尼DRωR是跟速度成正比的,输出负载为
| $ {M_{\rm{L}}} = n{F_{\rm{T}}}R - {D_{\rm{R}}}{\omega _{\rm{R}}}。$ | (17) |
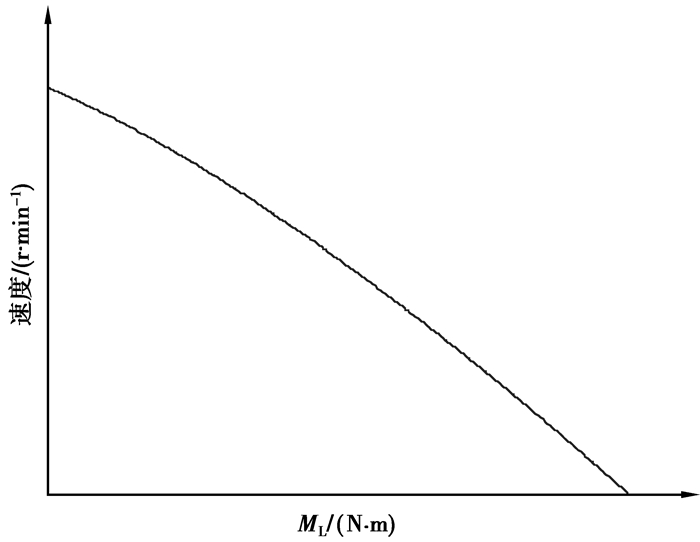
从式(17)中可以得到,当转速越快的时候在转子轴向上的阻尼消耗就越大。图 3为当x0=x1时转速和输出转矩的关系曲线。
|
图 3 为x1=x0时转速随着转矩变化的曲线 |
前文从理论上讨论了行波型超声电机在满足李雅普诺夫稳定性条件下制动区间与驱动区间的相对关系,得到了行波型超声电机稳定运行时的区间。
负载转矩经过变化可得
| $ \begin{array}{*{20}{c}} {{M_{\rm{L}}} = nR \cdot 2\mu {C_{\rm{N}}}{w_{\rm{A}}}\left[ {2\left( {\frac{1}{k}\sin k{x_1} - {x_1}\cos k{x_0}} \right) - } \right.}\\ {\left. {\left( {\frac{1}{k}\sin k{x_0} - {x_0}\cos k{x_0}} \right)} \right] - {D_{\rm{R}}}{\omega _{\rm{R}}}。} \end{array} $ | (18) |
将式(18)表示成ωR为自变量,并将式(6)代入式(18)中,有:
| $ \begin{array}{*{20}{c}} {{M_{\rm{L}}} = nR \cdot 2\mu {C_{\rm{N}}}{w_{\rm{A}}}\left\{ {\frac{2}{k}\sin \left[ {\arccos \left( {\frac{{{\omega _{\rm{R}}}R}}{{k{w_{\rm{A}}}\omega a}}} \right)} \right] - } \right.}\\ {\left. {\frac{2}{k}\arccos \left( {\frac{{{\omega _{\rm{R}}}R}}{{k{w_{\rm{A}}}\omega a}}} \right) \cdot \cos k{x_0}} \right\} - \mu R{F_{\rm{N}}} - {D_{\rm{R}}}{\omega _{\rm{r}}},} \end{array} $ | (19) |
可以得到行波型超声电机稳定运行时设计参数之间的关系,当预压力FN已知时可以由公式(8)直接求出x0,此时式(19)就只剩下ωR和ML 2个变量,当接触层的等效弹性系数CN、定子振幅WA、振动模态阶数n和有效接触半径R为已知的情况下,就可以得到李雅普诺夫稳定情况下ωR和ML的关系。反过来也可以在定ωR或ML的情况下确定其他2个参数的关系。
3 讨论| 表 1 超声电机仿真参数 |
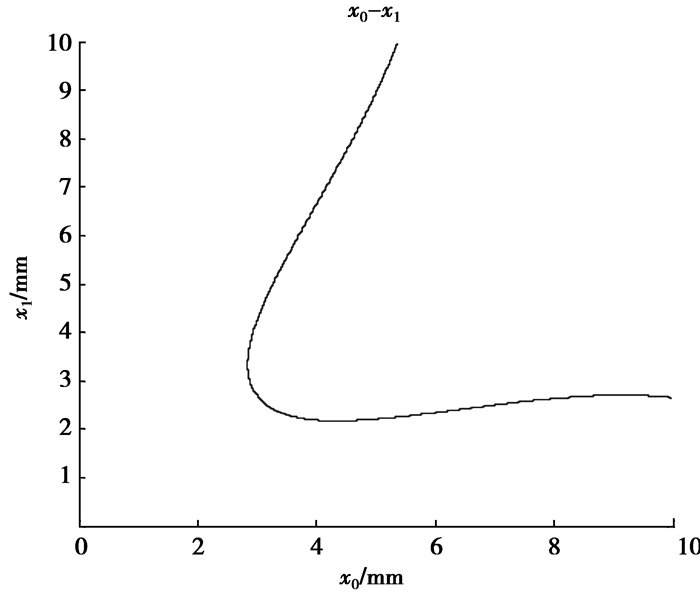
图 4为负载ML=0.120 0 N·m时x0和x1的关系曲线。
|
图 4 x0和x1的关系曲线 |
图 4中x0和x1临界点在x0=x1=2.129 mm时,即在[2.892,5.365]区间,每个x0都对应一个稳定的x1和一个不稳定的x1。
当预压力FN=55 N时,由式(8)或仿真波形图 4可以得到x0=3.332 mm。此x0对应图 4上的x1=2.376 mm和x1=5.164 mm。
此时,根据前文描述,当超声电机稳定运行时是不可能出现x0<x1的情况,所以认为x1=5.164 mm不满足实际的运行条件,x1=2.376 mm满足超声电机的运行理论。
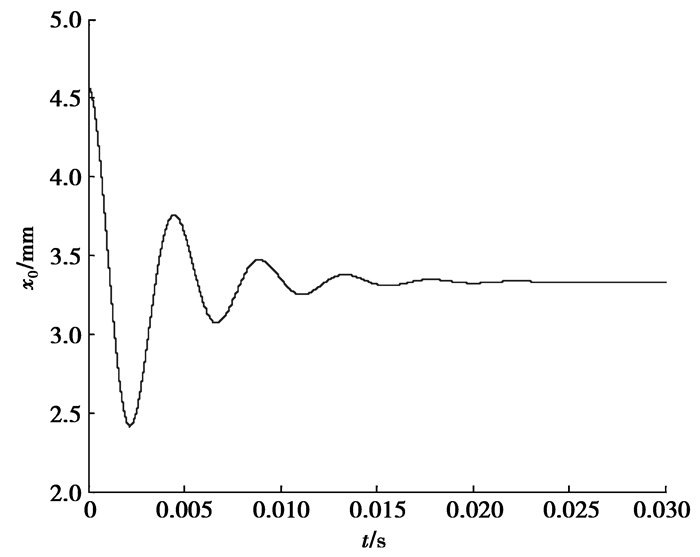
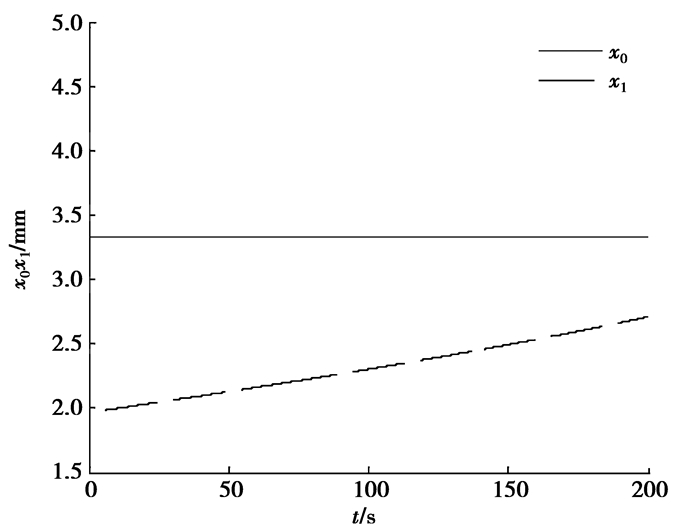
由式(7)、(8)和(9)可以推出,x0的位置只由预压力FN决定,而负载的影响是对驱动区间的影响即x1的大小。图 5是电机启动时x0的波动过程,图 6是预压力不变的情况下负载增加时x0和x1变化曲线,可以看到x1是随着负载的增大而增大,而x0由于预压力没有变化稳定在一个定值。
|
图 5 FN=55 N时x0的阻尼震荡 |
|
图 6 当负载增加时x0和x1变化曲线 |
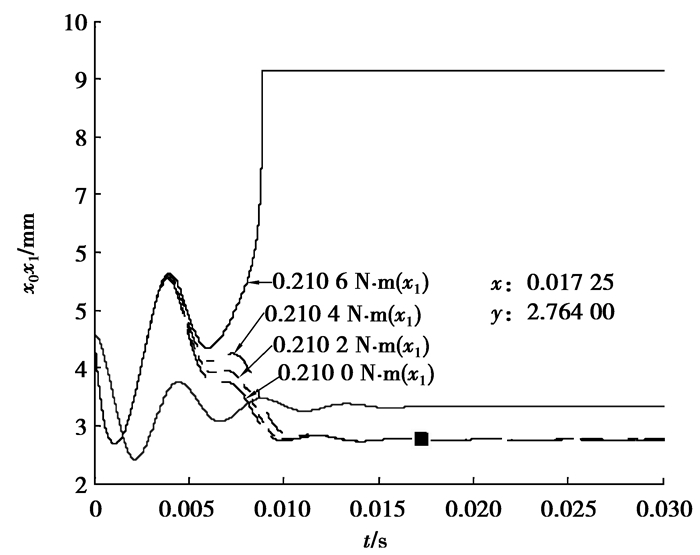
图 7为预压力FN=55 N时x0=3.332 mm,负载由0.210 0 N·m增加到0.210 6 N·m时x0和x1变化曲线,负载在0.210 0~0.210 4 N·m时x1经过阻尼振荡稳定下来的值都小于x0,而当负载为0.210 6 N·m时,经过一段时间的波动x1上升到x1=λ/2,此时仿真系统认定超声电机在外接负载的作用力下做反向运动,速度为负,而对应实际的情况为不可启动状态。根据计算可以得到当x1=x0=3.332 mm时,输出转矩ML的值是0.299 0 N·m,理论上当x1=x0时电机也能稳定运行,但在仿真中却始终找不到这一点,其原因可能是截断误差造成的。而在实际电机控制中对稳定要求必须要有一定的裕量,也不会运行在x1=x0状况下。
|
图 7 FN=55 N时转矩增加x0和x1变化曲线 |
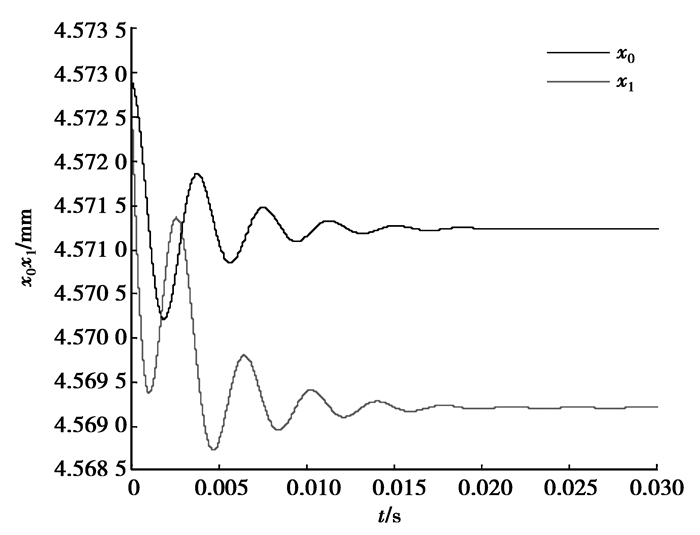
当预压力为125.6 N时x0=4.573 mm,如果此时的负载转矩ML=0.987 2 N·m,经过计算可以得到的x1=4.573 mm,转速为0,这是前文所描述的满足x1=x0=λ/4的临界状态。图 8和图 9是对这个参数状态的仿真波形。
|
图 8 x1、x0的仿真波形 |
|
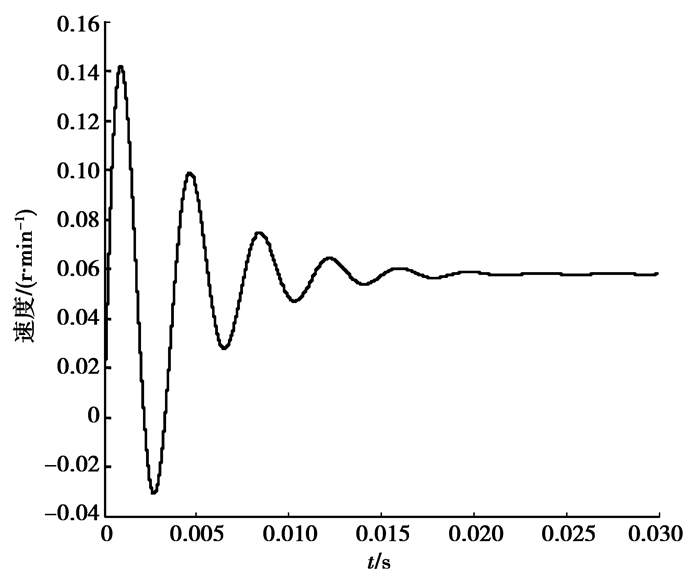
图 9 速度的仿真波形 |
从图 8和图 9可以看到,在这种情况下仿真得到的x0=4.569 3 mm,x1=4.571 2 mm,x1≈x0且速度稳定的时候为0.057 7 r/min。所以可以认为从仿真的角度验证了x1=x0情况的存在。
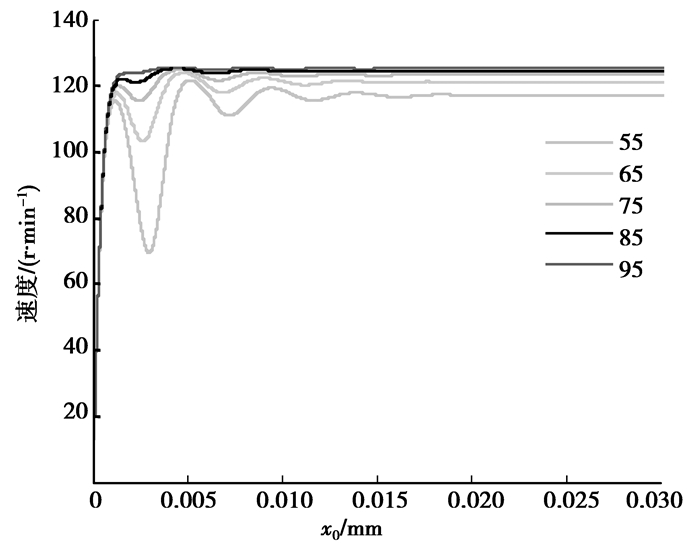
图 10为负载转矩为0.120 0 N·m时不同预压力所对应的不同速度曲线,从图中可知预压力为55 N时,速度在达到稳定之前的波动较大,并且稳定时的速度为117.3 r/min,当预压力为95 N时,速度在上升的过程中较为稳定,且稳定时的速度为125.3 r/min。
|
图 10 不同预压力所对应的速度曲线 |
由以上实验可以得到,预压力决定了x0的值,进而决定了x1的极限值,所以在对行波型超声电机进行设计时,预压力参数的选取直接决定了输出转矩极限。并且在设计电机预压力时可以根据转速和负载转矩的指标做折中选择。
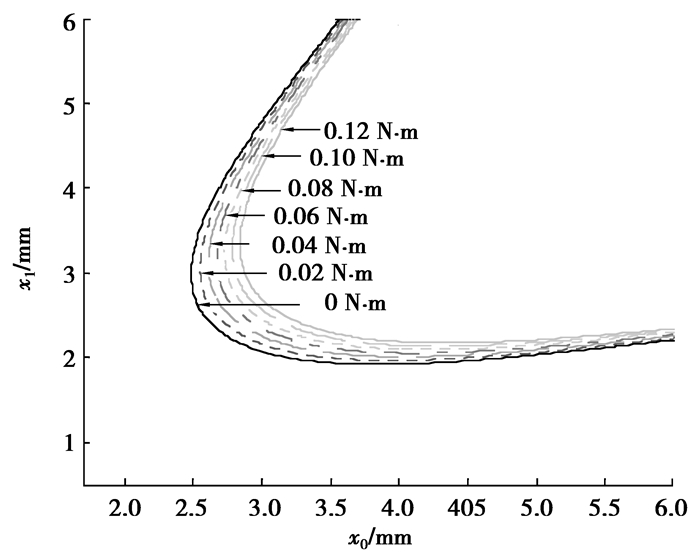
3.2 控制参数的讨论由式(18)可以知道x0和x1的关系曲线跟负载有一定的关系,当负载ML变化时曲线的位置将会发生如图 11所示的移动。
|
图 11 x0和x1随负载的变化的关系曲线 |
对于出厂后的超声波电机,在运行当中预压力是一个定值。当预压力确定时x0的稳定值可以通过式(7)和式(8)计算得到。
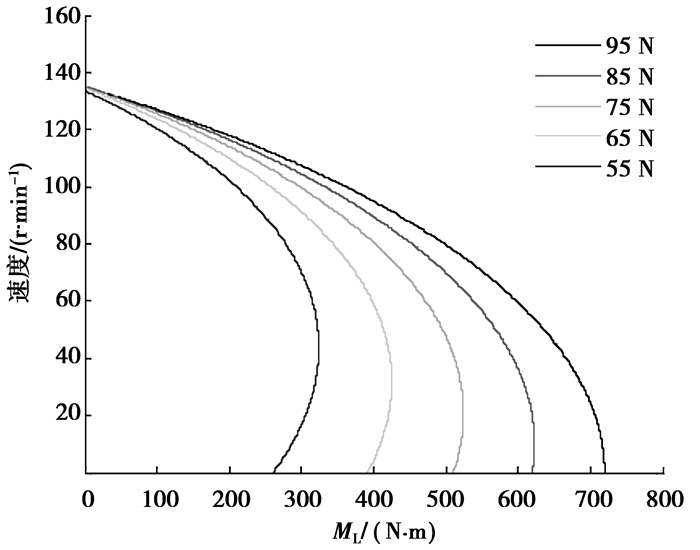
表 2为不同预压力下所对应的超声电机运行参数,图 12为不同预压力时转速对应输出转矩的曲线,即转速相对转矩变化的曲线。
| 表 2 不同预压力下超声电机运行参数 |
|
图 12 不同预压力时转速对应输出转矩的曲线 |
这里的nFRR和ML的单位都是N·m。当预压力增加时,如果负载转矩ML不变,x0将增大,同时x1的值减小,转速随着x1的减小而增大,根据式(9)可以知道当转速增加的时候转子获得的转矩增加,摩擦损耗增加。
图 12是满足李雅普诺夫平衡方程时不同预压力时转速对应输出转矩的曲线,当转速为0或者无限接近0的时候可以求得最大输出转矩即最大负载,但在实际的过程中由于转子阻尼系数的存在,在接近最大的负载的一段区域内所需要的驱动区间在很长的一段时间内都大于制动区间,即x1>x0,而当x1>x0时实际电机是停机的。超声电机在启动的一瞬间所需要的静摩擦力成倍于滑动摩擦力,所以实际运行超声电机所能带动的极限负载是小于理论值的。并且从图 12中可以看到,当预压力越大的时候速度相对于转矩变化的稳定性越好。
在对速度或者负载进行控制的时候就应该考虑到负载的变化与速度变化的相对影响,充分考虑到速度、负载和预压力3者之间的关系。
根据x0和x1随负载的变化的关系曲线(见图 6)和不同预压力时转速对应输出转矩的曲线(见图 12)来对实际电机的参数设计提供一定的方案:
1) 在提供了准确的预压力基础之上设计合适的运行速度和负载转矩范围;
2) 根据转速要求来设计合适的负载、预压力;
3) 根据需要的负载大小来设计合适的转速和预压力。
4 结论在研究数学模型基础上完成了超声电机的模型仿真并对速度满足李雅普诺夫平衡方程时的电机运行特性进行了讨论,根据李雅普诺夫平衡条件,讨论了驱动区间x1和制动区间x0的3种关系:
1) 当x0>x1时得到的满足李雅普诺夫平衡方程的实际解在x0和x1的关系曲线下半部分;
2) x0=x1在理论上存在,且并不是孤立的点,与确定的预压力、转速和负载转矩有着唯一固定的关系;
3) x0<x1在稳定运行的情况是不存在的。
驱动区间和制动区间的大小与超声波电机的预压力、驱动转矩、运行转速之间存在紧密关系。文中的研究结果为超声波电机的设计和运行控制提供参考价值。在运行时,要保证制动区间大于驱动区间,并留有一定的裕量。
| [1] | 史敬灼. 超声波电机运动控制理论与技术[M]. 北京: 科学出版社, 2011. |
| [2] | 张卫卫. 超声电机启动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. http: //cdmd. cnki. com. cn/Article/CDMD-10213-1011260719. htm |
| [3] | Maas J, Ide P, Fröhleke N, et al. Simulation model for ultrasonic motors powered by resonant converters[C]//Proceedings of the Thirtieth IAS Annual Meeting on Industry Applications, October 8-12, 1995, Oriando, Florida, USA. Piscataway:IEEE Press, 1995, 1:111-120. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=530291 |
| [4] |
陈如娟, 陈超, 宋小刚.
微小旋转型超声电机瞬态特性测试机机械特性估计方法[J]. 中国机械工程, 2011, 22(11): 1284–1287.
CHEN Rujuan, CHEN Chao, SONG Xiaogang. Transient test and estimation of mechanical properties of tiny rotary of ultrasonic motor[J]. China Mechnical Engineering, 2011, 22(11): 1284–1287. (in Chinese) |
| [5] |
周盛强, 赵淳生, 黄卫清.
旋转型行波超声电机接触界面的空间域分析[J]. 中国电机工程学报, 2010, 30(12): 63–68.
ZHOU Shengqiang, ZHAO Chunsheng, HUANG Weiqing. Contact analysis of traveling wave type rotary ultrasonic motor in space domain[J]. Chinese Society for Electrical Engineering, 2010, 30(12): 63–68. (in Chinese) |
| [6] |
张建桃, 张铁民, 梁莉.
超声电机非线性建模和广义预测控制[J]. 电机与控制学报, 2011, 15(6): 50–56.
ZHANG Jiantao, ZHANG Tiemin, LIANG Li. Nonlinear modeling and generalized predictive control of ultrasonic motor[J]. Electric Machines and Control, 2011, 15(6): 50–56. (in Chinese) |
| [7] | Bullo M, Perriard Y. Influences to the mechanical performances of the travelling wave ultrasonic motor by varying the prestressing force between stator and rotor[C]//Proceedings of 2003 IEEE Symposium on Ultrasonics, October 5-8, 2003, Honolulu, Hawaii. Piscataway:IEEE Press, 2003, 1:593-596. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1293473 |
| [8] | Chung S W, Chau K T. A new compliance control approach for traveling-wave ultrasonic motors[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 302–311. DOI:10.1109/TIE.2007.903936 |
| [9] | Iula A, Pappalardo M. A high-power traveling wave ultrasonic motor[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2006, 53(7): 1344–1351. DOI:10.1109/TUFFC.2006.1665083 |
| [10] | Qu J J, Wang Y L, Qu Y Y, et al. Study of gradient coating material for ultrasonic motor[J]. Tribology, 2009, 31(1): 25–29. |
| [11] | Qu J J, Tian X, Sun F Y. Experiment study on friction reduction of ultrasonic vibration based on traveling wave ultrasonic motor[J]. Tribology, 2007, 27: 73–77. |
| [12] | Juang PA, Tsai C C. Equivalent circuit modeling of an asymmetric disc-type ultrasonic motor[J]. IEEE Transactions on Instrumentation Measurement, 2009, 58(7): 2351–2357. DOI:10.1109/TIM.2009.2013928 |
| [13] | Giraud F, Semail B L, Aragones J. Precise position control of a traveling-wave ultrasonic motor[J]. IEEE Transactions on Industry Applications, 2007, 43(4): 934–941. DOI:10.1109/TIA.2007.900463 |
| [14] | Li H F, Zhao C S. Research on the ultrasonic motor driver base on LC resonant[J]. China Society for Electrical Engineering, 2008, 25(23): 144–148. |
| [15] | Huang S N, Tan K K, Lee T H. Adaptive sliding-mode control of piezoelectric actuators[J]. IEEE Transactions on Industrial Electronics, 2009, 56(9): 3514–3522. DOI:10.1109/TIE.2009.2012450 |
| [16] | 胡敏强, 金龙, 顾菊平. 超声波电机原理与设计[M]. 北京: 科学出版社, 2005. |
| [17] | 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2007. |
| [18] |
刘锦波, 陈永校.
超声波电机定转子接触的摩擦传动模型及其实验研究[J]. 中国电机工程学报, 2000, 20(4): 59–63.
CHEN Jinbo, CHEN Yongxiao. Investigation on contact model of ultrasonic motor and its experiments[J]. Chinese Society for Electrical Engineering, 2000, 20(4): 59–63. (in Chinese) |
| [19] | 赵淳生. 超声电机技术与应[M]. 北京: 科学出版社, 2007. |
 2014, Vol. 37
2014, Vol. 37

