b. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045
b. College of Civil Engineering Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing University, Chongqing 400045, China
中国西部地区典型的山地地貌特征使得桥梁往往桥墩较高,而经验表明钢筋混凝土桥梁的震害往往发生在桥墩部位,因此作为整个桥梁结构重要的受力构件,桥墩的设计对于桥梁结构抗震能力具有举足轻重的作用。近年来,基于性能抗震设计理论进一步发展。而桥梁的抗震设计,也从传统的基于承载力设计发展为延性抗震设计,并逐步向基于性能的抗震设计方向发展[1-2]。中国《公路桥梁抗震设计细则》(JTG/T B02-01—2008)对公路桥梁设计采用两水准设防、两阶段设计,即是初步体现了基于性能抗震设计的理念。然而我国规范并未给出基于性能需求的变形性能量化指标,而性能量化指标对于结构在地震作用下的各种性能状态和破坏形态的合理评估至关重要。目前,在钢筋混凝土桥墩的抗震性能设计方面,国内学者对常见的钢筋混凝土空心墩和实心桥墩进行了实验和理论分析方法的研究[3-4]。陆本燕等[5]在分析了圆形桥墩试验结果的基础上,将性能水准分为5等,选用位移角作为性能指标,验证了位移角指标对于长细比小于10的桥墩的适用性。刘艳辉[6]针对高架桥墩,推导出了以位移延性系数为性能指标的设计方法。宋晓东[7]对长细比为8的桥墩试验发现位移延性能系数有其片面性,提出了结合位移延性、等效滞回阻尼等多项参数的综合指标。
上述对桥墩性能设计及评估的研究主要是集中于中、低墩。对于长细比大于10的高墩的抗震性能,李建中等[8]分析探讨了高墩的位移延性能力,发现高墩的延性能力受地震荷载、高阶振型效应、墩身质量等因素的影响较大。梁智垚[9]在对比高墩与低墩的地震反应后认为在应变、曲率及位移3个基本的构件性能指标中,墩顶位移作为高墩的性能指标是不合适的。为此,文中在对高墩地震反应特性分析的基础上,研究适合于高墩的性能评价参数,并给出对应各性能水准的量化值,以期为钢筋混凝土高墩抗震性能的合理评估提供参考。
1 性能水准的划分为了实现结构基于性能的抗震设计,需选择合适的性态水准和设防水准,并由此定义性态目标。美国联邦紧急救援署(FEMA)、美国加州结构工程师协会(SEAOC)以及国内的部分学者[5-6]对性能水准的划分进行了详细研究。根据高墩的地震反应特性,文献[6],以结构材料应变作为界定基准,将高墩的性能水准划分为5个性能水准,即完好(完好,结构、构件功能正常可靠)、基本完好(轻微损伤,不需要修理)、轻微破坏(破坏,桥梁基本功能不受影响,一般修理后可继续使用)、中等破坏(破坏,大修后方可使用,基本功能受影响)及严重破坏(破坏严重以致修复不可行,基本功能已不能保障)。通过桥墩的宏观破坏情况将性能水准与裂缝宽度联系起来,进而得到与各性能水准对应的钢筋混凝土结构材料应变限值,如表 1所示。
| 表 1 高墩材料应变性能参数 |
目前国内外学者基于性能设计的方法集中在位移的设计研究,性能指标的研究集中于顶部位移延性系数及位移角。其中刘艳辉结合截面应变推导出的桥墩位移延性系数指标[6]如表 2所示,陆本燕总结分析国内外127个钢筋混凝土桥墩实验得到的位移角性能指标[5]如表 3所示。两者的性能水准都划分为5类,要求基本一致。
| 表 2 墩顶位移延性系数和位移角限值 |
| 表 3 位移角限值 |
虽然材料应变可以较为准确地描述构件进入弹塑性阶段时的损伤状态,但是需要建立精细到每一根钢筋和每一小条混凝土的精细模型,并且输出大量的信息,通过海量输出信息来判断构件损伤状态的过程显然是不现实的。截面曲率作为连接材料应变与墩身变形的纽带,既具有描述构件损伤状态的便利又可以采用相对简化的单元模型以提高计算效率,且较之位移指标更能反映结构内部破坏状态。因此文中以截面曲率作为研究对象,采用曲率延性系数作为性能水准的量化指标。
2.2.1 屈服曲率屈服曲率的计算公式很多,这里采用Priestley提出的桥墩结构在轴压比0~0.4,纵筋率0.01~0.04范围内,矩形截面等效屈服曲率的估算公式[10],
| ${\phi _y}D = 2.14{\varepsilon _y} \pm 10\% ,$ | (1) |
其中:
对于高墩柱普遍采用的箱形截面,可在矩形截面柱计算公式的基础上做一定修正。由式(1)知,当两截面的轮廓尺寸、所用材料及配筋相同时My、E基本相等时,两截面屈服曲率差异的主要因素为截面惯性矩。若箱形截面内边长d与外边长D之比为k,则箱形截面的惯性矩为
| ${I_x} = 0.0833\left( {1 - {k^4}} \right){D^4} = \left( {1 - {k^4}} \right)I。$ | (2) |
将式(2)代入式(1),则箱形截面的等效屈服曲率为
| ${\phi _{yx}} = {\phi _y}/\left( {1 - {k^4}} \right)。$ | (3) |
当已知箱形墩的截面尺寸,则可以通过式(1)、式(3)得到该箱形墩的近似等效屈服曲率为
| ${\phi _{yx}} = \left( {2.14{\varepsilon _y} \pm 10\% } \right)/\left[ {\left( {1 - {k^4}} \right)D} \right]。$ | (4) |
这里的极限曲率,不是仅指与截面最大塑性变形能力对应的曲率,而是依据表 1所规定的各性态水准下钢筋和混凝土材料的应变限值,假定平截面,通过力学关系推导得到的各个性能水准下的截面曲率。极限曲率的几何意义如图 1所示。
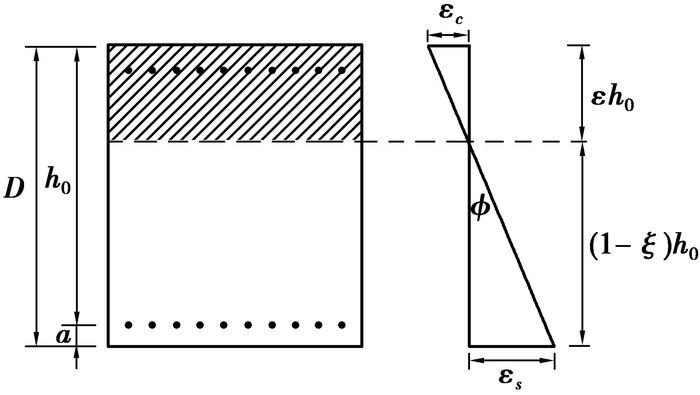
|
图 1 截面曲率示意图 |
| ${\phi _u} = \frac{{{\varepsilon _c}}}{{\xi {h_0}}} = \frac{{{\varepsilon _s}}}{{\left( {1 - \xi } \right){h_0}}} \approx \frac{{{\varepsilon _c}}}{{\xi D}} = \frac{{{\varepsilon _s}}}{{\left( {1 - \xi } \right)D}},$ | (5) |
其中,相对受压区高度
性能水准1:ϕu1=0.007/D;性能水准2:ϕu2=0.009/D;性能水准3:ϕu3=0.025/D;性能水准4:
| ${\phi _{u4}} = 0.055/D;性能水准 5:{\phi _{u5}} = 0.085/D。$ | (6) |
曲率延性系数是式(6)中各性能水准的极限曲率与式(4)中屈服曲率的比值,对箱型截面可得
| ${\mu _\phi } = \frac{{{\phi _u}}}{{{\phi _{yx}}}},$ | (7) |
结合式(4)和式(6)可得轴压比0~0.4,纵筋率为0.01~0.04范围的箱形墩柱截面曲率延性指标限值如下。
性能水准1:μϕ=0.003 3(1-k4)/εy;性能水准2:μϕ=0.0042(1-k4)/εy;性能水准3:μϕ=0.011 7(1-k4)/εy;性能水准4:μϕ=0.026(1-k4)/εy;
| $性能水准5:{\mu _\phi } = 0.04\left( {1 - {k^4}} \right)/{\varepsilon _y}。$ | (8) |
基于Opensees平台建立90 m高的单墩模型。墩底固结,墩身质量集中在相应节点上,与墩柱相邻跨的上部结构质量M集中在墩顶处,墩顶质量为700 t。沿墩身高度截面为正方形箱型截面,边长为4.4 m,壁厚0.5 m。墩轴压比为0.13,配筋率1.48%。桥墩采用材料为混凝土C40,纵筋HRB335。墩身采用弹塑性纤维梁柱单元模拟,其中混凝土纤维本构模型采用Kent-Park模型, 钢筋纤维采用双直线模型。沿墩高取单元长度为2 m。由以上基本参数可得k=0.8、εy=15E-4,代入式(4)得到屈服曲率为
| ${\phi _{yx}} = \frac{{1.69 \times 2.14{\varepsilon _y}}}{D} = \frac{{54.4 \times {{10}^4}}}{D}。$ |
将其与式(6)中对应的各性能水准极限曲率值分别代入式(8),可得到该墩对应于各个性能水准的曲率延性系数量化值如表 4所示。
| 表 4 曲率延性系数指标 |
采用增量动力分析法(incremental dynamic analysis,IDA)[11]分析桥墩在不同地震强度激励下的反应,IDA方法即是将1条地震波通过加速度峰值(PGA)调幅扩展为1组地震波,并利用这组地震波对结构进行动力时程分析。分析过程中,以桥墩内钢筋初次屈服时对应的墩底截面曲率为屈服曲率ϕy,此时对应的墩顶位移为屈服位移△y;以每次时程分析中得到的墩底截面最大曲率为该PGA下的最大曲率ϕu,得到的最大墩顶位移为该PGA下的最大位移△u;最大位移△u与屈服位移△y的比值即为墩柱的位移延性系数μm;△u与墩高的比值即为位移角θ;最大曲率ϕu与屈服曲率ϕy的比值即为墩柱的曲率延性系数μϕ。IDA分析中,由1条地震波调幅得到1组不同强度的地震波,从而得到对应的曲率延性系数、位移延性系数与位移角,将它们与表 2~表 4中所列的曲率延性系数范围、位移延性系数范围与位移角范围对比,便可分析出在该加速度峰值地震波作用下,以不同性能指标作为评定标准而得到的结构所对应的性能水准,从而对3类性能指标进行比较分析。
文中共选取3条不同频谱的地震动,作为动力时程分析时的输入地震动,其数据来源于太平洋地震工程研究中心的地震波数据库,分别命名为E1、E2、E3。为了进行IDA分析,对每条地震波都通过加速度峰值调幅进行扩展,峰值大小从0.1 g开始以步距0.1 g逐步增大,直至结构破坏。
3.3 结果分析 3.3.1 结构反应分析高墩进行动力时程增量分析,图 2~图 4给出了不同峰值大小的E1地震动输入下沿墩身高度各截面混凝土压应变、位移、曲率的反应极值分布。可以看出,曲率与应变的契合度较好,尤其是在墩身中部附近,由于高墩高阶效应的影响,应变与曲率都表现出了很明显的增大,而位移则无法体现相应的局部振动响应。由此可见,截面曲率可以较为准确地描述高墩进入弹塑性阶段时的损伤状态。
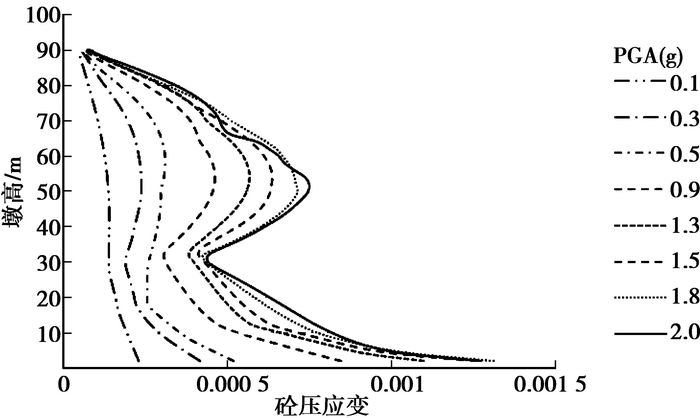
|
图 2 E1各PGA下90 m墩沿墩高的混凝土应变分布 |
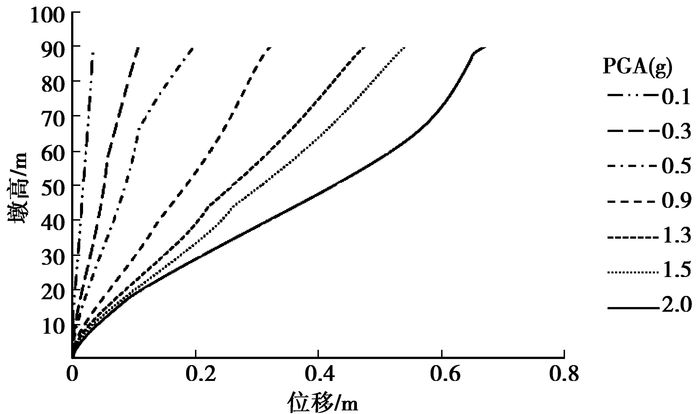
|
图 3 E1各PGA下90 m墩沿墩高的位移分布 |
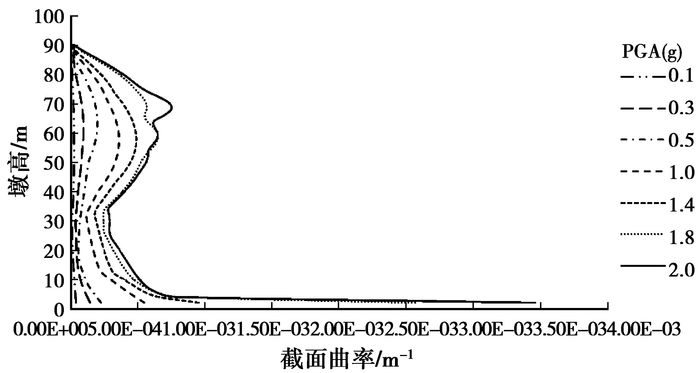
|
图 4 E1各PGA下90 m墩沿墩高的曲率分布 |
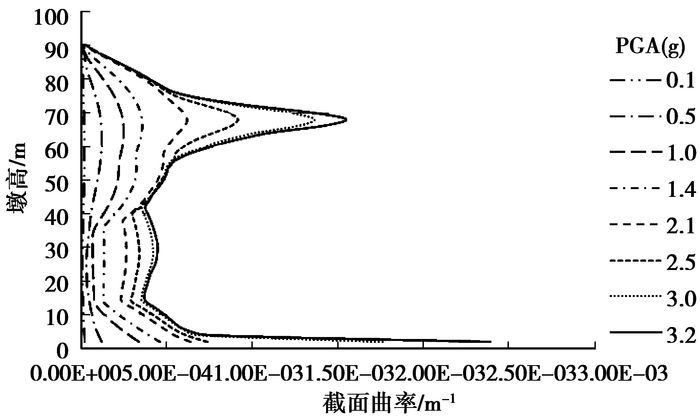
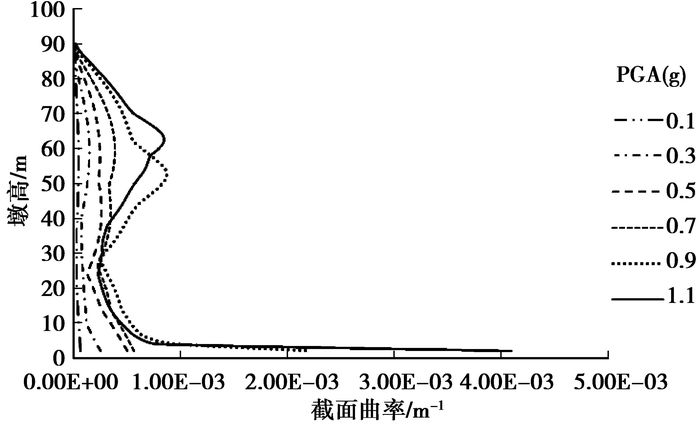
图 4~图 6绘出了3条不同地震波作用下沿墩身高度截面曲率的反应极值分布。可以看出,高墩由于高阶振型影响,墩柱曲率沿墩身分布形状呈较复杂的高次曲线,在墩身中部也可能出现曲率较大的情况。地震动的频率特性对结构的反应有较大影响,比较图 4~图 6,E1波作用下墩底截面曲率均是最大的,可选用墩底截面曲率作为判定依据。而在E2地震波激励下,高阶振型受地震激励的激发更明显,墩身中部截面曲率在较高强度地震作用下激增,可以看到当PGA达到0.5 g~0.6 g、2.2 g~2.8 g时,其墩身中部曲率(PGA=0.5 g~0.6 g时墩高62 m处;PGA=2.2 g~2.8 g时墩高68 m处)甚至超过了墩底。在E3地震波作用下,屈服破坏都较早;墩身中部的某些截面受到地震作用小时其截面曲率反而有可能更大,但不同强度地震激励下墩底截面曲率仍然始终是最大。由此可见,曲率延性指标对于结构性能的评估在一定程度上依赖于关键截面的选择。
|
图 5 E2各PGA下90 m墩沿墩高的曲率分布 |
|
图 6 E3各PGA下90 m墩沿墩高的曲率分布 |
为评价90 m高墩在不同强度地震作用下的抗震性能水平,分别输入3条地震波激励,并改变地震波峰值大小,得到不同强度地震波作用下高墩的曲率延性指标、墩顶位移延性指标和位移角指标,并由表 1~表 4中的判定依据确定结构相应的性能水准。由于材料应变可以较为准确地描述构件进入弹塑性阶段时的损伤状态,给出按混凝土压应变确定的性能水准作为比较基准。分析比较结果如表 5~表 7所示。鉴于3.3.1节中所分析的E2地震动作用下墩身中部截面曲率超过墩底的情况,PGA=0.5 g~0.6 g时墩高62 m处的截面曲率延性系数分别为0.218、0.268;PGA=2.2 g~2.8 g时墩高68 m处截面曲率延性系数为1.27、1.41、1.56、1.71、1.87、2.04、2.21,都与对应的墩底曲率延性系数相差不大且处于同一性能水准下。因此对于计算模型仍然可选用墩底截面进行性能评估。
| 表 5 E1作用下90 m墩各性能指标对比 |
| 表 6 E2作用下90 m墩各性能指标对比 |
| 表 7 E3作用下90 m墩各性能指标对比 |
可以看到,3个性能指标所界定出的性能水准间是存在差异的,而与能直接反映结构内部破坏本质的应变指标相比,曲率延性指标契合度明显高于位移延性指标和位移角指标,其契合度大致为曲率延性指标>位移延性指标>位移角,尤其是在更能激发高阶振型影响的E2地震动作用下以及在PGA较高的强震下,当位移延性指标和位移角指标都严重失真时,曲率延性指标仍然与应变指标保持很好的一致性,说明曲率延性指标能更好的反映高墩柱的性能水准。
4 结论根据钢筋混凝土高墩的地震反应特性,提出采用更适合于钢筋混凝土高墩柱的曲率延性指标对其进行抗震性能评价,并推导出不同性能水准下该指标的量化值。以90 m的高墩作为实例,并以应变指标为基准,对曲率延性指标、位移延性指标和位移角指标用于高墩抗震性能评价的适用性进行对比分析,可知高墩柱振动特性复杂,高阶振型的贡献明显,因此适用于低墩的性能指标不再适用于高墩。对于钢筋混凝土高墩而言,曲率延性指标相比于位移延性系数和位移角指标更为合理可靠,尤其是在强震作用下能够更准确反映墩柱的内部破坏情况。
实例分析表明以墩身最大曲率截面或墩底截面的曲率延性系数所得到的性能水准相差并不大,可直接采用墩底截面的曲率延性系数作为评价指标。但由于钢筋混凝土高墩柱的曲率响应规律比较复杂,更多高墩柱模型的分析评价将进一步研究。
| [1] | Jara M, Casas J R. A direct displacement-based method for the seismic design of bridges on bi-linear isolation devices[J]. Engineering Structures, 2006, 28(6): 869–879. DOI:10.1016/j.engstruct.2005.10.016 |
| [2] | Mackie K R, Lu J C, Elgamal A. Performance-based earthquake assessment of bridge systems including ground-foundation interaction[J]. Soil Dynamics and Earthquake Engineering, 2012, 42: 184–196. DOI:10.1016/j.soildyn.2012.05.023 |
| [3] | Shim C S, Chung C H, Kim H H. Experimental evaluation of seismic performance of precast segmental bridge piers with a circular solid section[J]. Engineering Structures, 2008, 30(12): 3782–3792. DOI:10.1016/j.engstruct.2008.07.005 |
| [4] | Papanikolaou V K, Kappos A J. Numerical study of confinement effectiveness in solid and hollow reinforced concrete bridge piers:Methodology[J]. Computers & Structures, 2009, 87(21/22): 1427–1439. |
| [5] |
陆本燕, 刘伯权, 刘鸣, 等.
钢筋混凝土桥墩性能指标量化研究[J]. 中国公路学报, 2010, 23(6): 50–56.
LU Benyan, LIU Boquan, LIU Ming, et al. Quantitative research on reinforced concrete performance index of reinforced concrete bridge column[J]. China Journal of Highway and Transport, 2010, 23(6): 50–56. (in Chinese) |
| [6] | 刘艳辉. 基于性能抗震设计理论的城市高架桥抗震性能研究[D]. 成都: 西南交通大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10613-2009057172.htm |
| [7] | 宋晓东. 桥梁高墩延性抗震性能的理论与试验研究[D]. 上海: 同济大学博士学位论文, 2004. http://d.wanfangdata.com.cn/Thesis/Y746282 |
| [8] |
李建中, 宋晓东, 范立础.
桥梁高墩位移延性能力的探讨[J]. 地震工程与工程振动, 2005, 25(1): 43–48.
LI Jianzhong, SONG Xiaodong, FAN Lichu, et al. Investigation for displacement ductility capacity of tall piers[J]. Earthquake Engineering and Engineering Vibration, 2005, 25(1): 43–48. (in Chinese) |
| [9] | 梁志垚. 非规则高墩桥梁抗震设计理论研究[D]. 上海: 同济大学, 2007. http://d.wanfangdata.com.cn/Thesis/Y1228181 |
| [10] | Priestley M J N. Brief comments on elastic flexibility of reinforced concrete frames and significance to seismic design[J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1998, 31(4): 246–259. |
| [11] | Vamvatsikos D, Cornell C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491–514. DOI:10.1002/(ISSN)1096-9845 |
 2014, Vol. 37
2014, Vol. 37

