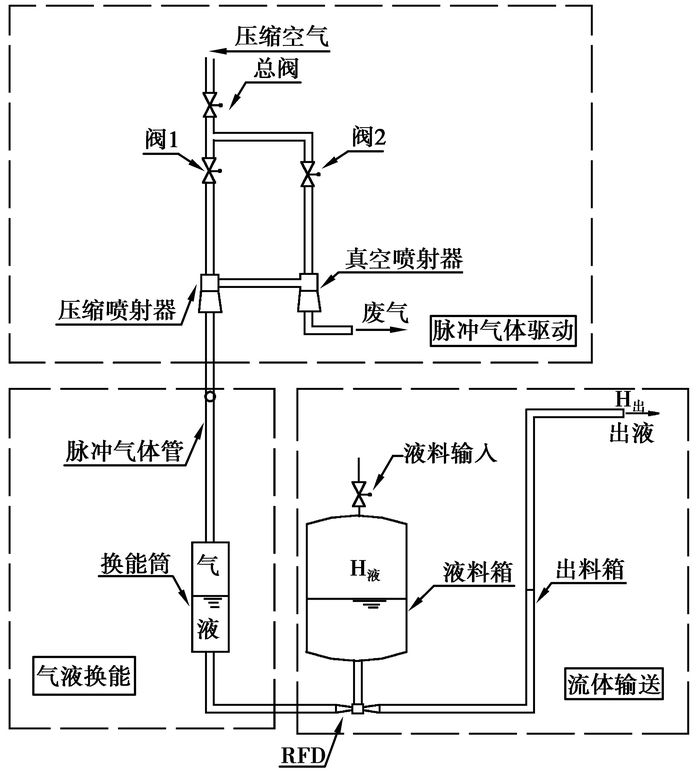
RFD(reversed flow device)装置是一种依靠流体动力输送介质的免维修流体输送装置。如图 1所示,其工作原理主要是利用压缩空气作为驱动力,通过真空喷射器和压缩喷射器将脉冲气体转换为脉冲液体,最后在周期性的脉冲液体驱动下,由RFD间歇性地将液体送输送至目的地。由于完全采用流体动力,装置不含运动部件,因此适用于需要免维修的危险流体输送场合。前英国核燃料有限公司(BNFL)70年代初开始研发此项技术,其专利转让到美国后,BNFL与AEAT合作对该技术进行了研发和推广,首先对用于输送和搅拌的400多套流体装置进行设计、制造及性能试验;其次对流体原理进行研究以进一步开发流体动力技术(power fluidics)在其他领域的应用,其研究为解决不同组合型式的流体装置尤其是RFD提供了一定的试验经验及理论支持。由于实际装置在材料、加工及不同几何特性上与试验装置的区别,往往使其装置性能与研发基地的试验数据发生偏差,因此仍需要对每一套工业装置进行原型试验[2-5]。其后处理厂中利用RFD进行放射性核废料液体(或泥浆)的输送(transport)、搅拌(mixing)、取样(sampling)已有30多年的历史[6-7]。中国从90年代开始关注该项技术,并在设计领域与原理试验方面取得了初步成果[8-12]。由于RFD装置在服役期内,人体无法近距离接触维修,因此必须避免运行中输送液体因空化而造成的效率下降、噪声及振动等威胁系统安全的运行工况。目前尚未见到相关文献,为此,文中拟针对特定的RFD装置设计,重点讨论RFD运行中空化发生条件,为RFD装置的工业应用提供理论依据。
|
图 1 RFD装置组成示意图 |
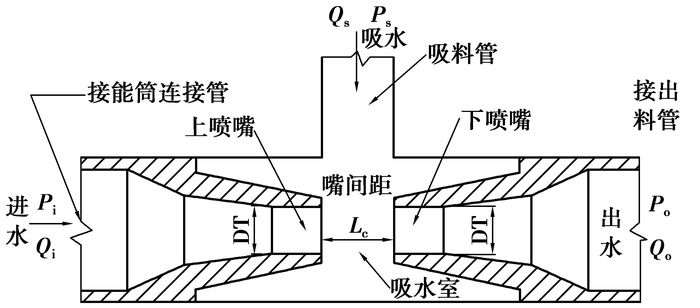
RFD具有与射流泵相似的结构(见图 2),设计工况下,在压冲阶段其上喷嘴工作流体将直接进入下喷嘴,吸入管不产生或很少产生引射流量。因此RFD仿真模型的选择可以借鉴射流泵数值模拟经验[13]。大量研究表明k-ε模型在模拟射流泵时有较好的精度和稳定性;关于空化问题,基于王国玉的广义密度理论[14],将液、汽视为混合相,依据气泡增长模型式(1)及空化发生标准式(2)计算汽泡空化凝结的半径,并由此计算混合密度,采用混合模型求解[15]。
|
图 2 RFD内部结构示意图 |
rayleigh-plesset方程:
| $\frac{{{P_B}\left( t \right) - {P_\infty }\left( t \right)}}{{{\rho _l}}} = R\frac{{{{\rm{d}}^2}R}}{{{\rm{d}}{t^2}}} + \frac{3}{2}{\left( {\frac{{{\rm{d}}R}}{{{\rm{d}}t}}} \right)^2} + \frac{{4{v_l}}}{R}\frac{{{\rm{d}}R}}{{{\rm{d}}t}} + \frac{{2\gamma }}{{{\rho _l}R}},$ | (1) |
式中:PB为气泡表面压力;P∞为当地远场压力;ρl为液相密度;R为空泡半径;γ是表面张力。空化判别标准:
| $\frac{{\partial u}}{{\partial x}} > \frac{{P - {{\bar P}_{\rm{V}}}}}{{2\mu }},$ | (2) |
式中PV是替代饱和蒸汽压PV的经验值,与温度、表面张力和吉布斯自由能有关。
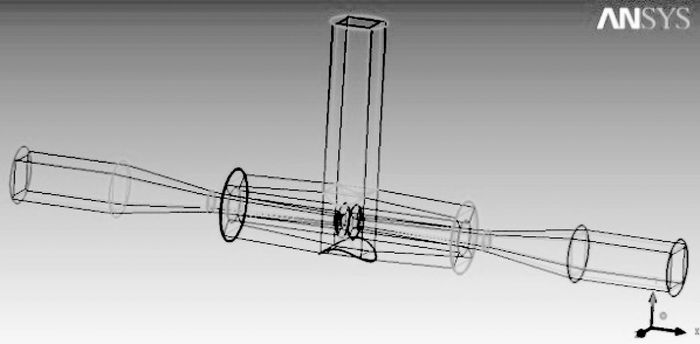
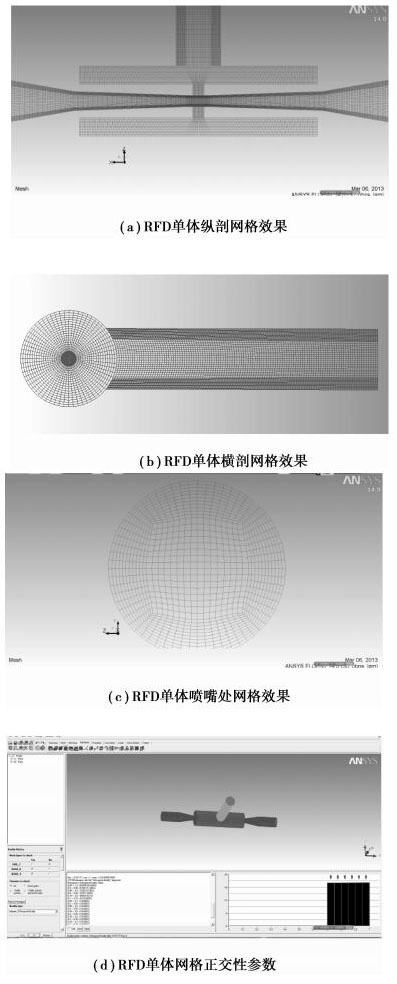
2.2 网格划分RFD是整套装置中最关键的输送部件,包括上、下喷嘴、吸水室以及进料管、出料管等。其外部结构类似三通,由于运行时RFD内部为周期性的正、反向流动,因此采用对称的上、下喷嘴,嘴间距是优化运行的关键尺寸。根据优化设计得出的RFD进行物理域造型和结构分块(见图 3),获得了如图 4所示的高质量正交网格。
|
图 3 RFD单体网格划分块的生成 |
|
图 4 RFD网格效果图 |
RFD单体边界有3个端口,将RFD上游进口及吸料管设为压力入口边界(pressure inlet),RFD出料管设为压力出口边界(pressure outlet)。为保证RFD三端管流充分发展,将上、下游的进、出口设置在距RFD上、下喷嘴大约1 m远处,RFD进料管取0.5 m远处。
2.4 计算处理实际应用中,空化模型时须采用绝对压力,迭代时亚松驰因子可设为气体体积分数为0.2~0.3,气泡质量采用0.1,以保证稳定的收敛速度。
3 压力参数对性能影响仿真试验 3.1 仿真试验方案笔者前期研究中已获得RFD关键尺寸的配套关系[13],文中就RFD工作压力、出口背压等运行因素对RFD空化发生条件进行仿真分析,设计仿真试验,并考虑到空化模型的计算量,对3种喷嘴直径dt压力为0.2~0.5 MPa范围的约10种压冲压力Pi以及3种出料管背压Po(10、15、20 m)进行仿真,考查各压力因子对RFD压冲流量Qo及水力效率η等运行特征的影响,观察并统计初生空化对应的压力参数。
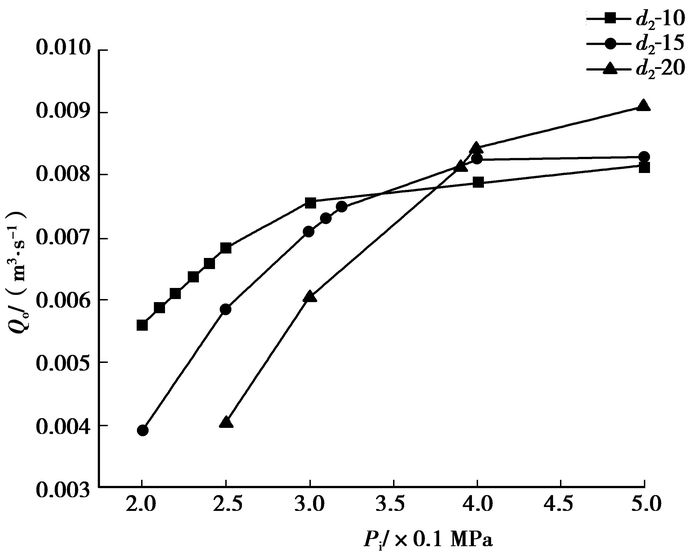
3.2 仿真分析 3.2.1 压冲参数的影响根据对3种RFD上喷嘴直径(由小到大为d1, d2, d3)的仿真分析,压力参数对出流量和效率的影响呈现了相同的变化趋势。以d2为例,随着压冲压力Pi的增大,出流量Qo的增加呈现先快后慢直至平稳的趋势,且背压Po越高出流量Qo越小(见图 5);分流比则呈现先增大后减小,即先分流后引射最后又出现分流的现象(见图 6),且随出料管背压Po的增加出现引射现象的工作压力Pi范围越窄,原因是当压冲压力Pi较小时,上喷嘴处未形成引射,RFD上、下喷嘴之间有部分流体分流至液料箱,而加大Pi后,喷嘴速度提高,出口压力下降形成负压产生引射(分流比上升),而当引射增加到下喷嘴的接受工作和引射水流的极限后,下喷嘴由于流速过高,可能发生空化,水流冲击损失和相变的耗能显著,并形成阻力,RFD重新出现分流现象(分流比下降),而这种分流比先增后减的现象会因为RFD出口背压Po的增加变得更加显著。
|
图 5 RFD-d2在不同背压下压力-流量曲线 |
|
图 6 RFD-d2在不同背压下压力-分流比曲线 |
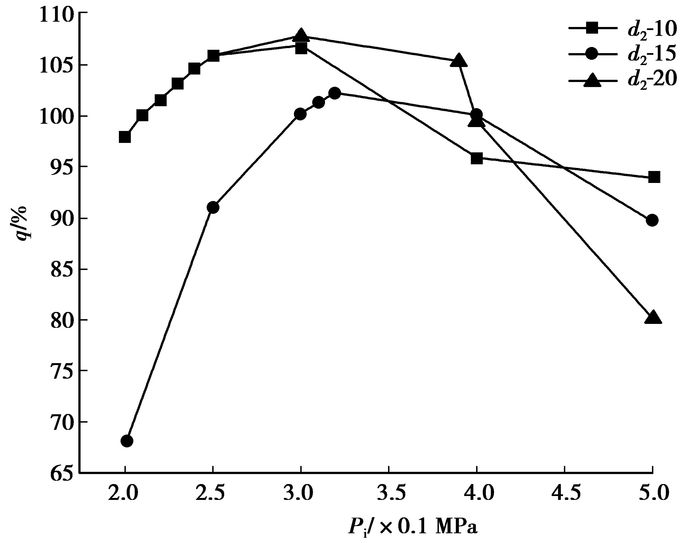
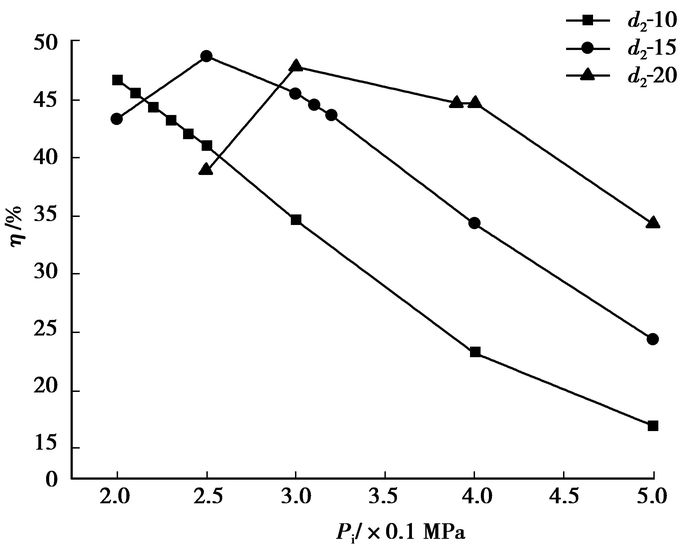
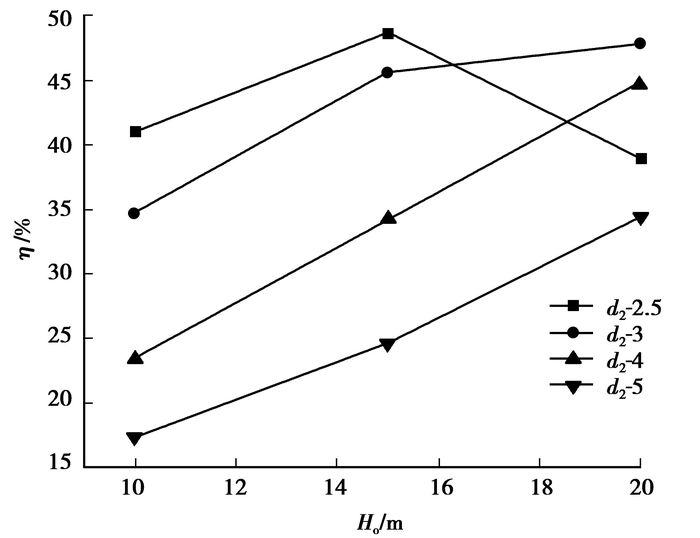
如图 7所示,随压冲压力Pi增加,效率曲线呈先增后减趋势且有极大值,在Pi增加初期,效率随装置平均流量Qav的增大快速上升,但当Pi增加到一定程度后,下喷嘴产生拥堵直至产生空化,过流量开始下降,RFD内部的能量损耗上升,效率降低。在不同压冲压力Pi下的RFD背压Ho与效率曲线如图 8所示,表示有1个最优的压冲压力Pi使得效率最高(本例0.3 MPa),且随背压加大,效率先升后降,即具有效率极值。
|
图 7 RFD-d2在不同背压下压力-效率曲线 |
|
图 8 RFD-d2在不同Pi下的背压-效率曲线 |
由此可见,无论是压冲压力还是RFD出口背压,均有1个流量和效率均较高的范围,取其交集,结合分流比接近1为控制空化发生的假设,RFD应在效率曲线的高效区范围(最高效率80%范围)运行,计算举例见表 1所示。由于该运行范围未考虑空化发生的限制,而在免维修的流体输送系统中,空化的危害是显而易见的,因此必须进一步讨论如何通过控制运行中的压力参数,以防止空化的产生。
| 表 1 3种喷嘴直径的最佳压力范围 |
在所讨论的RFD喷嘴直径范围内,压冲压力Pi一定时(如Pi<0.3 MPa),喷嘴直径越大,流量越大,而当压冲压力增加到一定程度(如Pi>0.4 MPa)之后,在扬程较低时,平均流量随着喷嘴直径的增长速度减缓,且当背压增大至20 m后,流量随喷嘴直径的增大呈现先增后减的趋势。这种现象发生的原因是,压力过大后RFD首先在下喷嘴发生空化,此时如果背压较低,流量可继续增大,而当背压到达一定高度时,阻力及空化的原因将降低RFD输水能力。相对同样的喷嘴直径而言,抗空化性能越好,其输水能力越强,因此研究并揭示RFD的空化性能是非常重要的。
上述分析中,RFD工作的最优组合参数如下:喷嘴直径比为3时,压冲压力Pi约为0.36 MPa,出口背压Ho为15 m;此时,RFD的效率约为33%,平均流量约为5 m3/h。
4 压力参数对空化影响仿真试验 4.1 空化现象数值仿真分析前文针对3种喷嘴直径的RFD进行了不同压冲压力和出口背压的数值仿真,通过分析RFD内部的流场和压力场对出流量和效率的影响,预测其空化发生范围。标况下,如场内的最低压力达到-0.0965 MPa,则认为RFD内部发生了空化,以下针对2种RFD直径比(RFD三端直径与喷嘴直径为直径比),进行初生空化的仿真,部分结果见表 2所示。计算发现,较小的直径比对空化防护有利。
| 表 2 RFD仿真结果空化分析表 |
表 2显示了2种直径比do/dt发生空化的临界压力条件,图 9和图 10分别显示了当背压为10 m时,直径比do/dt=3.1和4.3时的RFD压冲压力分别为0.25 MPa和0.21 MPa,说明直径比小的RFD比较不容易发生空化,由于直径比小的RFD下喷嘴到出料管的水力损失较大,当引射流体与工作流体汇合后,流速动能的增加受到限制,抑制了压力的过度降低,因此抑制了空化的发生。反之,相同的压冲压力下,出料管背压越大,下喷嘴入口的负压也将受到抑制,空化较不容易发生。

|
图 9 RFD(do/dt=3.1)空化现象(Pi=0.25 MPa,Po=10 m) |

|
图 10 RFD(do/dt=4.3)空化现象(Pi=0.21 MPa,Po=10 m) |
综上所述,为防止RFD运行中空化的产生,首先应提出压力操作的极限参数。未发生空化且效率较高的RFD最佳工作范围如表 3所示。
| 表 3 空化极限工作范围 |
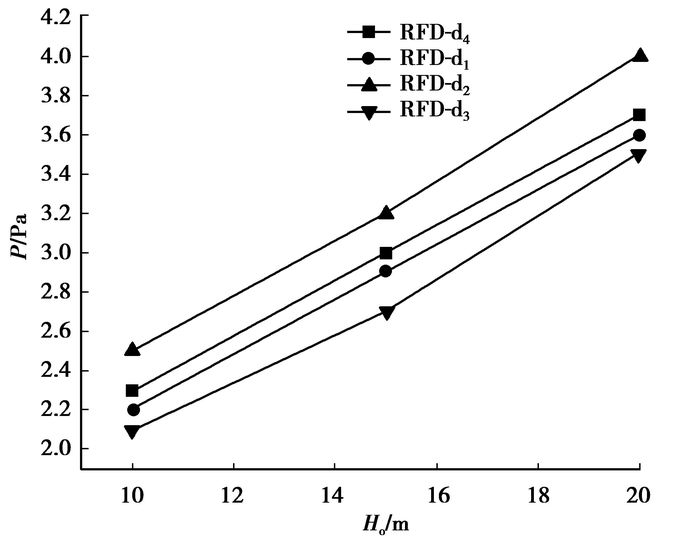
对照表 1中的不考虑空化问题的压力工作范围,可发现考虑空化后,压冲压力的上限将比仅仅考虑流量和效率最优的运行范围下降至80%~90%,由于RFD发生空化的临界点与直径比及出料管背压有关,对于较大直径比(4左右)和较小出料管背压(扬程为10 m)的RFD,压冲压力的这个限制取80%为宜。将所计算的4种喷嘴直径的RFD空化发生条件在图 11汇总。由图 11可以看出,RFD的空化极限工作压力与扬程(出料管背压)的比值近似为2~2.5,扬程较小或RFD直径比较小的取大值,即根据RFD所需扬程按2~2.5倍放大,即可大致估算RFD的空化极限工作压力,相对误差约为±10%。
|
图 11 各RFD空化临界工作压力图 |
分析了RFD装置运行中可能出现的空化问题。对其关键元件进行了压力操作参数的仿真,结合数值仿真分析,对特定RFD结构下的压力操作参数进行了讨论。
1) RFD出流量随工作压力的增加而增加,达到出料管输送极限后出流量不再增加,而RFD装置的平均流量、效率由于整个周期(压冲和反吸)的延长而呈先增后减的趋势,同时,随着压冲压力的增大,分流比呈现先增后减的趋势,即低压条件的RFD出现分流,压力提升后出现引射,压力再提升,由于进入下喷嘴接收不了过大流量而重新出现分流。由此,得出以流量和效率为优化目标的操作压力范围。
2) RFD的空化将发生在较高压冲压力时,仿真得出该临界压力与RFD的工作扬程(背压)和RFD直径比有关,相同条件下,直径比越小、扬程越高越不容易发生空化。
3) 实际操作过程中将压冲压力设置在低于表 1所示的压冲压力范围的80%~90%范围,以防止空化发生。针对RFD所需扬程,按工作压力与扬程之比为2~2.5倍,确定计算RFD压冲压力,可保证不发生空化。
RFD的结构与射流泵类似,在文献[16]的试验研究中,龙新平认为射流泵即便发生空化,空泡一般也不会在管壁上破裂造成汽蚀破坏,因此初步推想RFD也同样具有较好的抗汽蚀破坏性能。虽然如此,由于空化出现在操作压力较高的情况下,将导致装置效率显著下降,引起系统振动和噪声,因此仍然需要从操作程序上进行限制,进一步对RFD的抗汽蚀性能进行系统试验,通过统计初生空化,获得更通用的空化判别准数表达式。
| [1] | Smith G V, Lewis B E. Design of a pulsed-mode fluidic pump using a venture-like reverse flow diverter[R]. Tennessee:OAK Ridge National Laboratory Press, 1987. |
| [2] | Smith G V, Counce R M. Performance characteristics of axisymmetric venturi-like reverse-flow diverters[J]. Journal of Fluid Control, 1986, 16(4): 19–39. |
| [3] | Morgan J G, Holland W D. Pulsatile fluidic pump demonstration and predictive model application[R].Tennessee:OAK Ridge National Laboratory Press, 1986. |
| [4] | Priestman G H, Tippetts J R. Characteristics of a double-acting fluidic pump with hot and cold water[J]. Journal of Fluid Control, 1986, 16(4): 18–33. |
| [5] | Robinson S M, Counce R M, Smith G V. Performance characteristics of a continuous-flow fluidic pump[J]. Industrial &Engineering Chemistry Research, 1987, 26(8): 1698–1704. |
| [6] | Crass D W. An evaluation of power fluidicsTM mixing and pumping for application in the singel shell tank retrieval program[C]. formerly Numatec Hanford Corporation, Richaland WA 99353, Mar. 2001. |
| [7] | Tesar V. Pump for extremely dangerous liquids[J]. Chemical Engineering Research and Design, 2011, 8(7): 940. |
| [8] |
李江云, 徐如良, 王乐勤.
可逆流体转换器装置优化设计及应用[J]. 中国机械工程, 2003, 14(23): 57–62.
LI Jiangyun, XU Ruliang, WANG Leqin. Optimizationdesign and the applicationof RFS system[J]. China Mechanical Engineering, 2003, 14(23): 57–62. (in Chinese) |
| [9] | 郭彦华. 核用气动式脉冲液体射流泵和涡流二极管泵性能实验研究[D]. 北京: 清华大学, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10003-2005036551.htm |
| [10] |
樊燕芳, 徐聪, 景山. 可逆流体转向装置性能的数学模型及参数计算[J]. 原子科学技术, 2009, 43(8): 705-710. FAN Yanfang, XU Cong, JING Shan.Atomic energyscience and technology, 2009, 43(8):705-710. http://d.wanfangdata.com.cn/Periodical/yznkxjs200908007 |
| [11] |
李江云, 陈友霖, 王健, 等.
RFD装置优化设计理论及方法研究[J]. 工程热物理学报, 2010, 31(10): 1675–1679.
LI Jiangyun, CHEN Youlin, WANG Jian, et al. Optimal designtheory andmethods of RFDset[J]. Journal of Engineering Thermophysics, 2010, 31(10): 1675–1679. (in Chinese) |
| [12] |
李江云, 王健, 胡少华.
基于数值仿真的可逆流体转换器的优化设计方法[J]. 武汉大学学报:工学版, 2010, 43(6): 747–751.
LI Jiangyun, WANG Jian, HU Shaohua. Based on numerical simulation of reverse flowdiverter(RFD)optimized design method[J]. Journal of Wuhan University:Engineering, 2010, 43(6): 747–751. (in Chinese) |
| [13] | Song X H, Park J H, Kim S G, et al. Performance comparison and erosion prediction of jet pumps by using a numerical method[J]. Mathematical and Computer Modeling, 2013, 57(1/2): 245–253. |
| [14] | Wang G Y, Senocak I, Shyy W, et al. Dynamics of attached turbulent cavitating flows[J]. Progress in Aerospace Sciences, 2001, 37(6): 551–581. DOI:10.1016/S0376-0421(01)00014-8 |
| [15] | ANSYS, Inc. ANSYS 14.0FLUENT Theory Guide[M]. Pennsylvania: TechnologyDrive Canonsburg, 2011. |
| [16] | Long X, Yao H, Zhao J. Investigation on mechanism of critical cavitating flow in liquid jet pumps under operating limits[J]. International Journal of Heat and Mass Transfer, 2009, 52(9/10): 2415–2420. |
 2014, Vol. 37
2014, Vol. 37

