2. 重庆大学 通信工程学院, 重庆 400044;
3. 国网重庆市电力公司, 重庆 400015
2. College of Communication Engineering, Chongqing University, Chongqing 400044, China;
3. State Grid Chongqing Electric Power Cdrp., Chongqing 400015, China
移动ad hoc网络(mobile ad hoc networks, MANET)具有灵活部署、快速机动等优点,但也存在带宽和能量受限、拓扑动态变化、可扩展性和安全性差等不足。分簇作为一种网络拓扑管理方式,具有3大优势:一是支持空间资源复用,能增大系统容量;二是簇头节点集合和网关节点集合能构成虚拟骨干网,路由生成和信息传播只在骨干网上进行,能降低路由建立开销;三是简化网络结构,易于管理和维护。但分簇生成和维护仍需要额外开销:簇结构的建立和维护涉及大量信息交互;节点移动或死亡等局部变化时,需要重新选举部分簇头甚至引发全局簇重构。由此可见,设计合理的分簇算法是提高簇稳定的关键。
分簇算法可以基于节点能量、位置、移动速度等参数,采用集中式或分布式方法实现。分簇过程中最重要的环节是确定簇头选择准则,这是因为簇头数影响着通信开销、传输延迟、簇内/簇间通信机制、簇更新策略等。
在MANET网络中,节点能量有限,为了均衡能耗,文献[5-6]以经典的LEACH算法为基础,综合考虑节点间距和剩余能量,提出的基于距离和能量的分簇机制能改善簇头选举和数据传输,降低由于节点无序分布而导致的簇头能耗过度问题。为了提高网络拓扑的稳定性,FENG等[7]充分考虑了节点移动性,并引入相对运动概念,选取运动较为稳定的节点成为簇头,并针对可能出现分簇集中度过高现象,在簇维护阶段引入快速簇分裂算法提高网络拓扑的稳定性。Chatterjee等[2]提出一种加权分簇算法(weighted clustering algorithm, WCA),簇头选举中考虑节点连接度差、邻节点距离和、平均移动速度和簇头服务时间等参数,使得簇头选举和簇维护过程更合理,但会增加通信开销,且各节点能耗不同,利用簇头服务时间无法评估节点能耗;Muth等[8]对WCA算法进行了改进,在簇维护阶段引入移动性预测机制,用于预测节点是否会随1跳邻节点移动,利用线性回归和簇形成降低通信开销。Wang等[9]通过限制节点作为簇头的服务时间,能均衡能耗;设置最小距离,能提高簇头服务可靠性。Hussein等[10]提出一种分布式加权分簇算法,利用节点连接度、剩余能量、平均移动性、距离4参数选择本地最佳簇头。该算法能在不降低网络性能、满足簇间负载均衡、减少通信开销、最大化簇结构稳定性的前提下选择最优簇头。Yang等[11]也提出一种加权分簇算法,考虑移动节点平均连接度和能量状态参数,以提高簇结构的稳定性,采用非周期性的基于需求的簇头选举,降低计算和通信开销。
为了增强MANET网络簇结构的稳定性,笔者提出一种多参数加权分簇算法。该算法综合考虑了节点剩余能量、邻居节点数、节点移动性3要素,并针对随机步行移动网络和参考点群组移动网络分别设计不同的节点稳定性参数,在随机步行移动网络中利用剩余能量参数、邻居节点参数和相对稳定性参数加权构成稳定性参数,而在参考点群组移动网络中采用剩余能量参数、邻居节点参数和移动相关性参数加权构成稳定性参数。
1 约束规则及加权参数设计 1.1 约束规则MANET网络在进行分簇时,节点存在待定(undetermined, UD)、簇头(cluster head, CH)和簇成员(cluster member,CM)3种状态,各节点依据以下约束规则参与分簇过程
1) 支配约束:节点至少存在一个邻居簇头节点,且只加入一个簇。
2) 簇加入约束:节点存在邻居簇头节点,且邻居簇头节点的稳定性参数值与当前所属簇头的稳定性参数值之差大于门限wth,该节点应加入稳定性参数值更大的簇。
3) 邻居簇头约束:相邻簇头节点的稳定性参数值之差大于门限wth时,数值较小的节点放弃簇头节点身份,加入数值较大的簇头节点管理的簇。
1.2 加权参数设计执行分簇时综合节点剩余能量、邻居节点数以及移动性3要素。假设节点能通过能量管理单元获得剩余能量信息;通过节点间的信息交互获取邻节点信息;通过辅助定位单元获得节点位置信息。
剩余能量参数:节点能量受限,一旦能量耗尽,将无法继续生存。由于簇头节点承载的负载大,必然会消耗更多能量,因此分簇算法必须考虑节点剩余能量,选择剩余能量较大的节点成为簇头。节点剩余能量参数定义为
| $ {E_i}\left( t \right) = {e_i}\left( t \right)/{e_i}\left( 0 \right), $ | (1) |
其中ei(t)为t时刻节点可用剩余能量,ei(0)为节点初始总能量。
邻居节点参数:簇头节点有一定数量的成员节点,成员节点越多,网络分簇后形成的簇越少,构成的虚拟骨干网络拓扑更简洁。节点周期性发送信标并监听来自其他节点的信标,然后提取源节点ID以构建邻居节点表。邻居节点数ni(t)是t时刻与节点i具有直接链路的1跳邻居节点数。邻居节点参数定义为
| $ {N_i}\left( t \right) = 1 - 1/{n_i}\left( t \right), $ | (2) |
当节点i孤立时,ni(t)=0,Ni(t)→-∞。
节点移动性参数:分别针对2种典型应用场景定义节点移动性参数,在随机步行移动网络[12]中称为相对稳定性参数,而在参考点群组移动网络[13]中称为移动相关参数。
相对稳定性参数:随机步行移动模型广泛用于刻画MANET网络中具有随机移动性的节点移动模式。相对稳定性参数用于描述节点的随机步行移动性,用以选举相对稳定的簇头节点。
假设节点能获知自身位置信息(xi(t), yi(t)),t时刻节点i, j之间的距离di, j(t)为
| $ {d_{i,j}}\left( t \right) = \sqrt {{{\left( {{x_i}\left( t \right) - {x_j}\left( t \right)} \right)}^2} + {{\left( {{y_i}\left( t \right) - {y_j}\left( t \right)} \right)}^2}} , $ | (3) |
节点i相对于节点j的移动速度mi, j(t)为
| $ {m_{i,j}}\left( t \right) = \left| {{d_{i,j}}\left( t \right) - {d_{i,j}}\left( {t - \Delta T} \right)} \right|/\Delta T, $ | (4) |
其中ΔT为时间差。mi, j(t)越小,表明节点i相对于节点j的移动越慢,反之亦然。节点i相对于邻节点集合中所有K个节点的相对稳定性定义为
| ${S_i}\left( t \right) = 1 - E\left[ {{m_{i,j}}\left( t \right)} \right]/{m_{{\rm{th}}}},$ | (5) |
式中:E[mi, j(t)]为节点i相对于所有邻节点的移动速度均值;mth为阈值,通常2倍于实际移动速度的最大值。
移动相关性参数:在参考点群组移动网络中,节点按照相互间的逻辑关系形成以逻辑中心为参考点的群组。参考点的移动模式决定了群组移动模式,节点移动由参考点的宏观移动轨迹确定,移动节点相对于参考点的位置随机分布,但均与参考点相邻,且每个节点都能独立随机移动。在参考点群组移动模型中,节点移动具有相关性,将移动性相似的节点分组,构建相对稳定的分簇结构。
假设节点i以时间T为周期发布分簇信令C(i),在此期间测量M次位置,τ=T/M,则
| $ \left\{ \begin{array}{l} \Delta x\left( m \right) = {x_i}\left( {t + m\tau } \right) - {x_i}\left( t \right);\\ \Delta y\left( m \right) = {y_i}\left( {t + m\tau } \right) - {y_i}\left( t \right), \end{array} \right. $ | (6) |
其中m=1, 2, …, M。节点从t到t+mτ的移动速度和移动方向分别为
| $ {v_i}\left( {t + m\tau } \right) = \sqrt {\Delta x{{\left( m \right)}^2} + \Delta y{{\left( m \right)}^2}} /m\tau , $ | (7) |
| $ \begin{array}{l} {d_i}\left( {t + m\tau } \right) = \\ \left\{ \begin{array}{l} \arctan \left| {\frac{{\Delta y\left( m \right)}}{{\Delta x\left( m \right)}}} \right| \cdot {\mathop{\rm sgn}} \left( {\Delta y\left( m \right)} \right),\;\;\;\;\Delta x\left( m \right) > 0;\\ \left( {{\rm{ \mathsf{ π} /2}}} \right) \cdot {\mathop{\rm sgn}} \left( {\Delta y\left( m \right)} \right),\;\;\;\Delta x\left( m \right) = 0;\\ \left( {{\rm{ \mathsf{ π} }} - \arctan \left| {\frac{{\Delta y\left( m \right)}}{{\Delta x\left( m \right)}}} \right|} \right) \cdot {\mathop{\rm sgn}} \left( {\Delta y\left( m \right)} \right),\;\;\;\;\Delta x\left( m \right) < 0。\end{array} \right. \end{array} $ | (8) |
从t到t+T,节点的宏观移动速度vi(t+T)和宏观移动方向di(t+T)分别为
| $ {v_i}\left( {t + T} \right) = \frac{1}{M}\sum\limits_{m = 1}^M {{v_i}\left( {t + m\tau } \right)} ; $ | (9) |
| $ {d_i}\left( {t + T} \right) = \frac{1}{M}\sum\limits_{m = 1}^M {{d_i}\left( {t + m\tau } \right)} , $ | (10) |
节点i与邻节点j在t时刻移动速度和方向的相关性定义为
| $ {R_s}\left( {i,j,t} \right) = \frac{{\min \left( {{v_i}\left( t \right),{v_j}\left( t \right)} \right)}}{{\max \left( {{v_i}\left( t \right),{v_j}\left( t \right)} \right)}}, $ | (11) |
| $ {R_d}\left( {i,j,t} \right) = \cos \left( {{d_i}\left( t \right) - {d_j}\left( t \right)} \right), $ | (12) |
移动相关性参数
| $ {R_{sd}}\left( {i,j,t} \right) = {R_s}\left( {i,j,t} \right) \times {R_d}\left( {i,j,t} \right), $ | (13) |
其中Rs(i, j, t)∈[0, 1],Rd(i, j, t)∈[-1, 1],所以Rsd(i, j, t)∈[-1, 1]。节点i的移动相关性参数是其相对所有K个邻居节点的移动相关性的均值
| $ {R_i}\left( t \right) = \frac{1}{K}\sum\limits_{j = 1}^K {{R_{sd}}\left( {i,j,t} \right)} 。$ | (14) |
多参数加权分簇算法综合考虑节点剩余能量参数、邻居节点参数以及节点移动性参数3要素。针对随机步行移动模型和参考点群组移动模型,分别定义不同的节点稳定性参数
| $ \left\{ \begin{array}{l} W_1^i\left( t \right) = {w_1}{E_i}\left( t \right) + {w_2}{N_i}\left( t \right) + {w_3}{S_i}\left( t \right);\\ W_2^i\left( t \right) = {w_1}{E_i}\left( t \right) + {w_2}{N_i}\left( t \right) + {w_3}{R_i}\left( t \right), \end{array} \right. $ | (15) |
式中wm∈[0, 1](m=1, 2, 3),且w1+w2+w3=1;节点稳定性参数Wni(n=1, 2)的上标i为节点编号,下标1表示针对随机步行移动网络、下标2表示针对参考点群组移动网络。权值wm可根据应用需求调整,如在节点能量受限的无线传感器网络中,剩余能量参数可赋予较高权值;如果侧重考虑节点移动性,可赋予节点移动性参数较高权值。权值分配的可调性使得该算法适用于多种网络环境。
各节点初始稳定性参数Wni(0)=0(n=1, 2),周期性发送分簇信令C(i),并接收来自邻居节点的分簇信令C(j)。信令消息包含节点ID(i)、状态St(i)、所属簇的IDc(i)、当前宏观移动速度vi(t)、宏观移动方向di(t)和稳定性参数Wni(t)。其中,状态St(i)∈{UD, CH, CM},初始时刻St(i)=UD;所属簇的IDc(i)为对应簇头节点的ID(i)。
以参考点群组MANET网络为例阐述多参数加权分簇算法流程,随机步行MANET网络加权分簇算法流程类似。分簇算法流程如图 1所示,节点计算自身稳定性参数,同时接收来自邻节点广播的分簇信令,更新邻节点集合;更新稳定性参数W2i(t),生成并发送分簇信令。比较节点i与邻节点的稳定性参数值,根据节点i的当前状态St(i)确定其新状态,有3种可能的情况。

|
图 1 参考点群组移动网络加权分簇算法流程 |
第一种:St(i)=UD。当节点i的邻节点集合中存在簇头节点c时,若节点i的稳定性参数值与邻居簇头节点的稳定性参数值之差大于门限wth,即W2i(t)>W2c(t)+wth,设置St(i)=CH、IDc(i)=ID(i),并向邻居节点发送分簇信令C(i),声明成为簇头节点;否则设置St(i)=CM、IDc(i)=ID(c),并发送分簇信令C(i)加入该簇。当邻居节点集合中不存在簇头节点时,若节点i的稳定性参数值大于所有处于UD状态的邻居节点的稳定性参数值,设置St(i)=CH、IDc(i)=ID(i),并发送分簇信令C(i),声明成为簇头节点;否则节点i继续保持UD状态。
第二种:St(i)=CH。当邻居节点集合中存在簇头节点c,且满足W2c(t)>W2i(t)+wth时,设置St(i)=CM、IDc(i)=ID(c),然后发送分簇信令C(i)声明放弃簇头身份,并加入该簇;当邻居节点集合中不存在簇头节点时,节点i将续担任本簇的簇头节点。
第三种:St(i)=CM。若节点i的邻居节点集合不包括自己的簇头节点,表明节点脱离了自己所属簇,设置St(i)=UD,IDc(i)=0,成为待定节点。然后按照St(i)=UD继续分簇流程。如果节点i的邻居节点集合存在多个簇头节点,稳定性参数值最大的簇头节点为k,若W2k(t)>W2i(t)+wth,设置St(i)=CM,IDc(i)=ID(k),并发送分簇信令C(i),声明离开原簇并加入簇头节点k对应的簇中;否则继续处于原簇中,St(i)=UD。
3 仿真分析与测试为了评估提出的多参数加权分簇算法的性能,将多参数加权分簇算法与MOBIC分簇算法[14]和HD分簇算法[15]分别针对随机步行移动模型和参考点群组移动模型进行仿真对比分析和测试。算法性能评价指标定义如下
簇头节点数NCH:网络分簇后形成的簇头节点数,与簇的大小成反比。
簇重入次数NRA:单位时间内节点切换所属簇头节点的平均次数,表征网络中成员节点变更所属簇的频度。
簇重构次数NRC:单位时间内簇头节点放弃簇头身份,引起网络重新分簇生成新簇头节点的平均次数。
3.1 随机步行移动模型下的仿真测试仿真参数设置为:节点随机均匀分布在1 000 m×1 000 m矩形区域,节点数50≤N≤500,移动服从随机步行移动模型,移动速度1~10 m/s,移动方向为0~360°,节点每隔1 s更新位置。通信范围100~200 m,节点每隔15 s进行一次簇更新。初始能量为1,剩余能量参数Ei(t)、邻节点参数Ni(t)以及节点稳定性参数Si(t)的加权系数w1=w2=w3=1/3,相对移动速度阈值mth=20 m/s,稳定性参数门限wth=0.2。进行50次仿真,每次仿真时长15 min,然后计算各评价指标的均值。
图 2所示为分簇形成的簇头节点数NCH随网络节点数N之间的变化关系。由图可知,随着网络节点数增大,3种算法的簇头数NCH都相应增大,但多参数加权分簇算法形成簇头数最少。这是由于该算法综合考虑了剩余能量参数、节点邻居参数和相对稳定性参数,节点移动时簇头能保持相对稳定,且保证邻居节点数多的节点优先成为簇头节点。
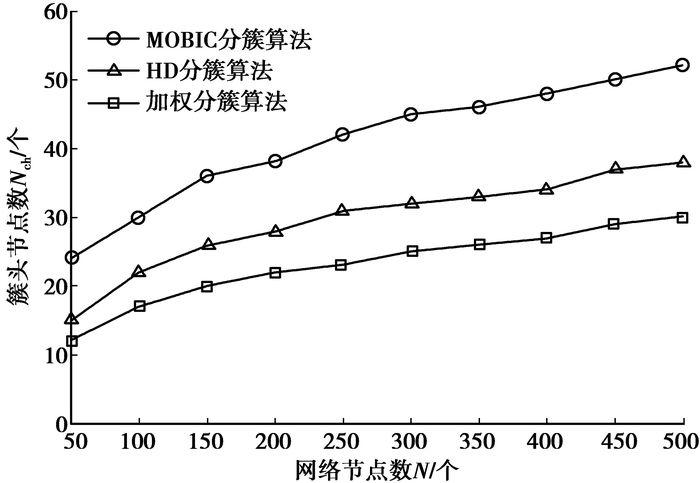
|
图 2 节点移动速度为5 m/s、通信距离为100 m时,簇头节点数与网络节点数之间的变化关系 |
图 3所示为簇重入次数NRA随节点移动速度的变化关系,表征节点移动速度对分簇结构稳定性的影响。由图可知,节点移动速度越快,发生簇重入的几率越大。节点移动显著影响分簇结构的稳定性,HD算法未考虑节点移动性,因此簇重入次数明显高于MOBIC算法和多参数加权分簇算法。多参数加权分簇算法综合考虑了节点的相对稳定性和邻居节点数,其簇重入次数略少于MOBIC算法。
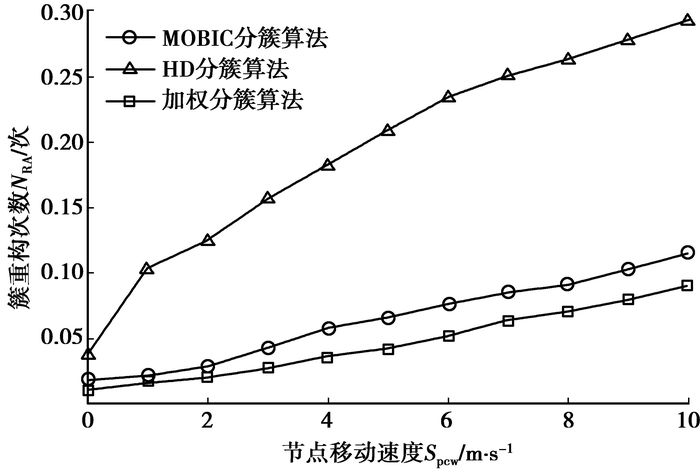
|
图 3 网络节点数为100、通信距离为200 m时,簇重入次数与节点移动速度之间的变化关系 |
图 4所示为簇重构次数NRC随节点移动速度的变化关系。簇重构次数受节点剩余能量、邻居节点数和节点移动性的影响,与簇重入次数的变化趋势基本一致。节点能量耗尽、移动或簇头相邻都可能发生簇头辞职或重选,进而引发簇重构。
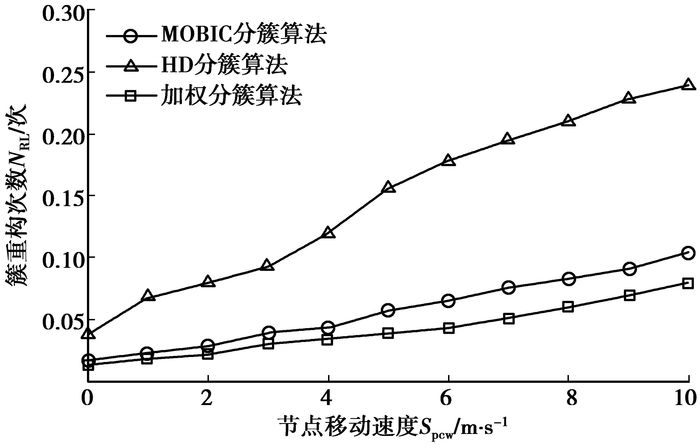
|
图 4 网络节点数为200、通信距离为200 m时,簇重构次数与节点移动速度之间的变化关系 |
节点移动服从参考点群组移动模型,各群组有一个虚拟参考中心,该参考中心的运动轨迹随机设置,其移动速度和方向确定了群组的移动模式,群组中各节点围绕虚拟参考中心随机移动并随参考中心移动,令w1=w2=1/4,w3=1/2,增大移动相关性在节点稳定性参数中的权重。
如图 5所示,随着网络节点数N增大,3种算法形成的簇头数NCH也随之增大,其中多参数加权分簇算法NCH形成的簇头数最少,3种分簇算法的NCH相对关系基本保持不变。

|
图 5 参考中心移动速度为3 m/s、通信距离200 m时,簇头节点数与网络节点数之间的变化关系 |
图 6中,随着节点移动速度增大,NRA随之增大。由于HD算法未考虑节点移动性,NRA明显高于MOBIC算法和多参数加权分簇算法,MOBIC算法考虑了节点的相对移动而非移动相关性,无法刻画节点的群组移动模式,而多参数加权分簇算法综合考虑了邻节点参数和节点移动相关性参数,簇重入次数最少。

|
图 6 网络节点数为200、通信距离为200 m时,簇重入次数与参考中心移动速度之间的变化关系 中文注解 |
簇重构次数NRC与参考中心移动速度、节点通信范围的变化关系如图 7和图 8所示。簇重构次数NRC受节点剩余能量、邻居节点数和节点移动相关性的影响,而多参数加权分簇算法综合考虑了这3个因素,相比之下,簇重构次数最少。

|
图 7 网络节点数为200、通信距离为200 m时,簇重构次数与参考中心移动速度之间的关系 |

|
图 8 网络节点数为200、参考中心移动速度为3 m/s时,簇重构次数与节点通信范围之间的关系 |
分簇是一种高效的网络拓扑管理机制,利用分簇算法得到的分层结构可以提高MANET网络的管理和运行性能。以典型的MANET网络分簇算法为基础,提出了一种多参数加权分簇算法。该算法综合考虑了节点剩余能量、邻居节点数、节点移动性3要素,分别针对随机步行移动网络和参考点群组移动网络的不同特征设计了不同的节点稳定性参数,在随机步行移动网络中利用剩余能量参数、邻居节点参数和相对稳定性参数加权构成稳定性参数,而在参考点群组移动网络中采用剩余能量参数、邻居节点参数和移动相关性参数加权构成稳定性参数。仿真分析和测试表明,基于本文确定的约束规则和节点稳定性参数加权准则,提出的多参数加权分簇算法形成的簇头节点数、簇重入次数和簇重构次数均小于仅考虑单一因素的HD分簇算法和MOBIC分簇算法,能有效提高网络分簇结构的简洁性和稳定性。
| [1] | Jamal N, Ai-Karaki, Ahmed E. Effcient virtual-backbone routing in mobile ad hoc networks[J]. Computer Networks, 2008, 52(2): 31–33. |
| [2] | Umamaheswari, Radhamani G. Clustering schemes for mobile ad hoc networks:a review[C]. 2012 International Conference on Computer Communication and Informatics(ICCCI), Coimbatore, 2012:1-6. |
| [3] | Zhou Z P, W T. An energy balanced cluster algorithm for wireless sensor networks[C]. 201224th Chinese Control and Decision Conference, Taiyuan, 2012:3843-3848. |
| [4] | Vodopivec S, Bester J, Kos A A survey on clustering algorithm for vehicular ad hoc networks[C]//201235th International Conference on Telecommunications and Signal Processing. Prague:IEEE, 2012:52-56. |
| [5] | Hu G, Xie D M, Wu Y Z. Research and improvement of LEACH for wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2007, 20(6): 1391–1396. |
| [6] | Zhu Y, Qing P. A energy-efficient clustering routing algorithm based on distance and residual energy for wireless sensor networks[C]//2012 International Workshop on Information and Electronics Engineering, 2012:1882-1888. |
| [7] | Feng W J, Wu D. A clustering algorithm based on link availability for MANT[J]. Journal of Chongqing University, 2010, 33(12): 109–113. |
| [8] | Muthuramalingam S, RajaRam R. A dynamic clustering algorithm for MANETs by modifying weighted clustering algorithm with mobility prediction[J]. International Journal of Computer and Electrical Engineering, 2010, 2(5): 709–714. |
| [9] | Wang H T, Chen H, Song L H. Improved AOW clustering algorithm for wireless self-organized networks and performance analysis[C]. 2012 cross strait quad-regional radio science and wireless technology conference, 2012:142-146. |
| [10] | Hussein A, Yousef S. An efficient weighted distributed clustering algorithm for mobile ad hoc networks[C]. International Conference on Computer Engineering and Systems, 2010:221-228. |
| [11] | Yang W D. Weight-based clustering algorithm for mobile ad hoc network[C]. Cross strait Quad-regional radio science and wireless technology coference. 2011:787-79. |
| [12] | Tolba F D, Magoni D, Lorenz P. connectivity, energy and mobility driven clustering algorithm for mobile ad hoc networks[C]. IEEE global telecommunications conference. 2007:2786-2790. |
| [13] | Gu Y Y. On the stability of ad hoc group mobility models[C]. IEEE International Conference on Communications (ICC'09). 2009:1-6. |
| [14] | Gu Y Y, Lu W D, Prasad R V. Clustering in ad hoc personal networks formation[J]. Computational Science-ICCS, 2007: 312–319. |
| [15] | Li D Q, Xue W H, Cao Q G. Research on ad hoc network clustering algorithm based on signal strength[C]. Proceedings of 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems.2010:719-722. |
 2014, Vol. 37
2014, Vol. 37

