2. 中国电子科技集团 第44研究所, 重庆 400060
2. China Electronics Technology Group Corporation No. 44 Research Institute, Chongqing 400060, China
为了保护图像安全,防止图像内容泄漏,特别是针对军事、医疗等方面的图像,需要进行加密处理。图像拥有方可以利用现有的图像加密算法[1-2]加密图像,保证图像的安全性,同时也需要对原始图像进行压缩,去噪,变换等图像处理。如果有大量图像需要专业处理,交给第三方设备进行处理会极大地提高处理效率。特别是在当前的云计算环境下,数据交由云端设备处理的优势日益彰显。此时,为了保障图像安全,图像拥有方往往会将图像加密之后再交给不受信任的第三方。这个时候,第三方就必须针对一副加密了的图像进行处理。图像加密后,隐藏了图像内容,使得图像失去了一定的相关性,因此,加密图像处理相对普通图像处理比较困难。近年来,也提出了一些加密图像处理算法[3-9],如水印,压缩,变换等处理,较好地实现了对加密图像的处理。然而,对于加密图像的去噪算法还是空白,一些效果好的非加密图像去噪方法在这里并不适用。
中值滤波是去除图像噪声的一种常用方法。它本质上是用像素邻域内的中间值代替该像素的像素值,以达到去噪和平滑的效果。但是,由于普通的中值滤波会遍历整幅图像,就会导致不是噪声的点也会被处理,使得滤波后的图像丢失细节,变得模糊。
为了解决这个问题,提出了开关中值滤波的算法和一些改进算法[10-15]。它分为检测阶段和滤波阶段。在检测阶段,利用预先设立的门限值,将噪声点和非噪声点区分开来,检测出噪声点。然后在滤波阶段,只对检测出的噪声点进行中值滤波处理。这样,就能够既去除噪声,又保留图像的细节部分。
在这样的背景下,提出了一种基于开关中值滤波的加密图像去噪算法,该算法能够较好地去除加密图像的噪声。
1 提出的算法提出的算法有3个步骤,图像加密,加密图像开关中值滤波和图像解密,算法框图如图 1所示。首先,图像发送方利用密钥对存在冲击噪声的图像进行加密,然后发送给图像处理方。图像处理方得到的图像是一副遮盖了图像内容的加密图像,并利用开关中值滤波的方法对其进行去噪处理,并将去完噪的图像传送给图像接收方。拥有解密密钥的图像接收方可以对图像进行解密,获得图像内容。
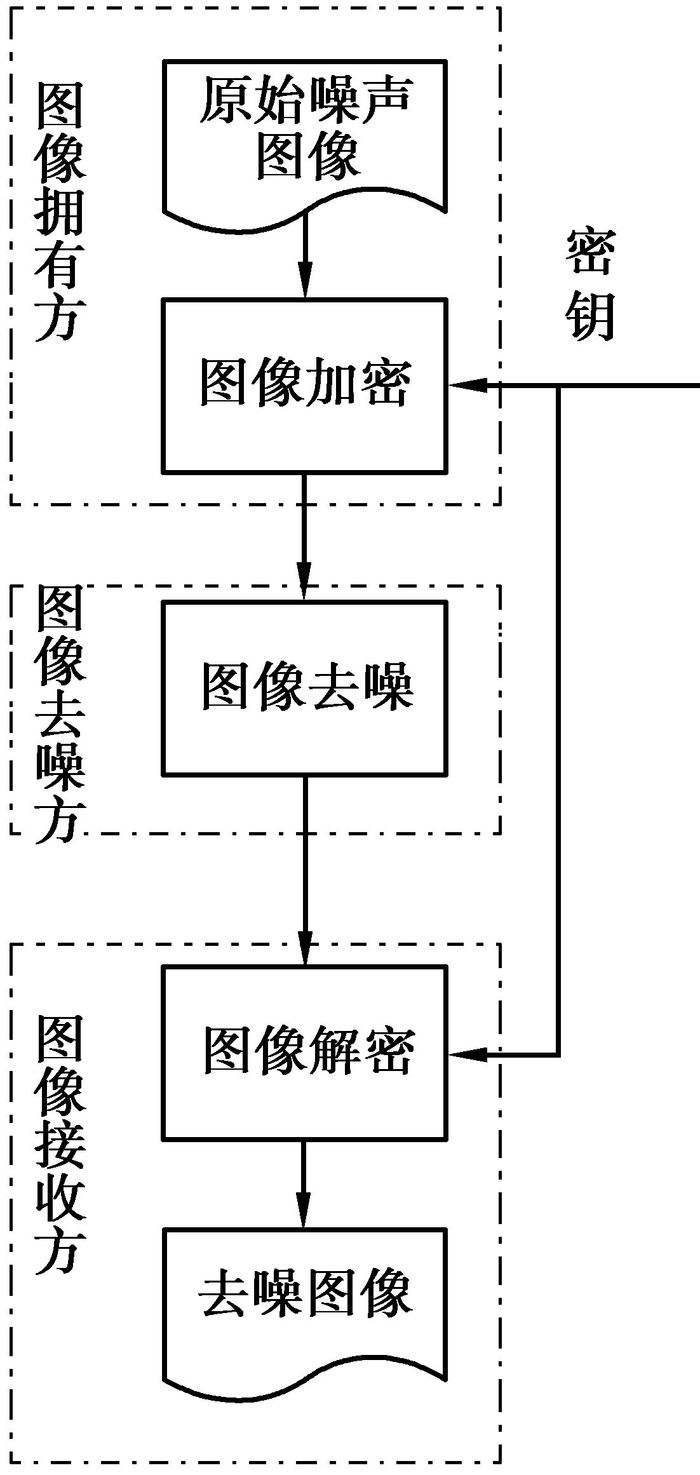
|
图 1 算法总体框图 |
下面,依次介绍这3个步骤。
1) 图像加密
根据算法的需要,采取的加密方式是一种像素位置置乱方法。
假设灰度图像I的大小是M×N,首先将图像分成大小是S×S的互不重叠的小块。这样,小块的个数一共是
2) 开关中值滤波
现在,图像处理方获得的图像是一副加密了的图像,而且他并不拥有密钥,因此不能获得原始图像。为了去除冲击噪声,图像处理方就必须对加密图像进行滤波处理。此时的开关中值滤波也分为2个阶段。
首先是检测阶段。图像处理方将加密图像同样分成大小是S×S的互不重叠的小块。将图像内像素点的值可以表示为Imi, nj,其中
| ${\mu _{m,n}} = \frac{1}{{{S^2}}}\sum\limits_{i = 1}^S {\sum\limits_{j = 1}^S {{I_{mi,nj}}} } ,$ | (1) |
| ${\sigma _{m,n}} = \sqrt {\frac{1}{{{S^2}}}\sum\limits_{i = 1}^S {\sum\limits_{j = 1}^S {{{\left( {{I_{mi,nj}} - \mu } \right)}^2}} } } 。$ | (2) |
然后,利用均值和标准差可以得到2个门限值,将小块内的像素点分成A、B 2个集合
| $\left\{ \begin{array}{l} {I_{mi,nj}} \in A,{I_{mi,nj}} < {\mu _{m,n}} - \omega \times {\sigma _{m,n}}\left\| {{I_{mi,nj}} > {\mu _{m,n}} + \omega \times {\sigma _{m,n}}} \right.;\\ {I_{mi,nj}} \in B,{\mu _{m,n}} - \omega \times {\sigma _{m,n}} \le {I_{mi,nj}} \le {\mu _{m,n}} + \omega \times {\sigma _{m,n}}, \end{array} \right.$ | (3) |
其中,参数ω∈[1, 2],是标准差的权值。一般情况下,自然图像在一个小块内图像点的像素值较为相近,噪声点的像素值会和图像点的像素值相差较大。这样,集合A里面的像素点被认为是噪声点,集合B里面的像素被认为是未受污染的图像点。
检测到噪声点之后,进行滤波阶段。这时采用传统的中值滤波的方法。在每一小块中,对像素值进行排序,并取它们的中间值medm, n。如果像素Imi, nj∈A,也就是说它是噪声点,那么令
| ${I_{mi,nj}} = {\rm{me}}{{\rm{d}}_{m,n}}。$ | (4) |
需要指出的是,提出的算法和传统的开关中值滤波算法有所区别。传统的开关中值滤波算法设置大小为S×S的窗口,在窗口内对窗口中心点进行检测和滤波,并且窗口按照一定顺序滑动,遍历整幅图像。提出的算法受到加密过程的限制,只能在每个小块内对块内的所有点进行处理,滤波效果会受到一定的影响。
3) 图像解密
图像处理方会将中值滤波处理之后的加密图像传送给图像接收方。而图像接收方是受图像发送方信任的,拥有图像解密密钥。因此,可以通过密钥将图像像素的位置恢复到原位,可以成功进行解密。解密之后的图像就是已经去除噪声了的图像。
2 实验结果笔者利用的实验图像是大小为512×512的灰度图像Lena和Baboon,即取M=N=512, 取S=4。加入椒盐噪声,噪声比例p=1%,2%,……,10%,将噪声图像分成4×4的互不重叠的小块, 对图像进行分块像素置乱加密。在图像去噪阶段,取参数w=1.7(经验值)。
表 1显示了在不同噪声比例下,噪声点的漏检概率、虚警概率和解密之后图像和原始图像相比的PSNR值。需要说明的是,表中漏检概率是未检测出的噪声点个数与噪声点个数的比值,虚警概率是误检出的噪声点与非噪声点个数的比值,表示开关中值滤波的质量;表中PSNR值是去噪图像与未加噪声的原始图像的峰值信噪比,表示去噪图像的质量,计算表达式如下
| 表 1 Lena图像在不同噪声比例下,噪声点的漏检概率、虚警概率和解密之后图像的PSNR |
| ${\rm{PSNR}} = 10 \cdot \lg \frac{{{{255}^2}}}{{{\rm{MSE}}}},$ | (5) |
其中,MSE是去噪图像和未加噪声的原始图像之间的均方误差。
从表 1中可以看出,随着椒盐噪声比例p的增大,图像噪声点的漏检概率增大,虚警概率减小,去噪之后图像的质量适当下降,但是整个去噪效果较为明显。
表 2显示了块的大小对滤波效果的影响。从表中可以看出,块的大小越大,恢复出的图像质量越不好,同时块的大小也不能太小。实验结果显示,取块的大小为4×4最为合适。
| 表 2 Lena图像在5%噪声比例下,取块大小分别为2×2,4×4,8×8和16×16时,解密之后图像的PSNR |
图 2和图 3是椒盐噪声比例p=5%时,原始图像,加入噪声后的图像,加密后的噪声图像和最终去噪并且解密后的图像的对比,选用了常用的标准Lena和Baboon图像测试。从图中可以看出,本算法能够较好的去除噪声,图像视觉效果良好。

|
图 2 Lena图像去噪效果对比 |

|
图 3 Baboon图像去噪效果对比 |
提出了一种加密图像的开关中值滤波算法。通过本算法,图像拥有者可以将加密图像交给第三方进行去噪处理,处理效果较好,能够去除绝大部分的噪声,图像细节丢失很少。提出的算法既能够达到去除噪声的目的,又能保证图像内容不被泄漏,很好地保护了图像的安全和隐私。
| [1] | Kumar A A, Makur A. Lossy compression of encrypted image by compressive sensing technique[C]//Proc. IEEE Region 10 Conf.[s.n]:IEEE, 2009:1-6. |
| [2] | Zhang X P. Lossy compression and Iterative reconstruction for encrypted image[J]. IEEE Trans. Inf. Forensics Security, 2011, 6(1): 53–58. |
| [3] | Bianchi T, Piva A, Barni M. On the implementation of the discrete fourier transform in the encrypted domain[J]. IEEE Trans. Inf. Forens. Security, 2009, 4(1): 86–97. DOI:10.1109/TIFS.2008.2011087 |
| [4] | Bianchi T, Veugen T, Piva A, et al. Processing in the encrypted domain using a composite signal representation:pros and cons[C]//Proc. IEEE WIFS.[s.n.]:IEEE:2009:176-180. |
| [5] | Zheng P J, Huang J W. Implementation of the discrete wavelet transform and multiresolution analysis in the encrypted domain[C]//Proc. of the 19th ACM international conference on Multimedia.[s.n.]:IEEE, 2011:413-422. |
| [6] | Lu W J, Swaminathan A, Varna A L, et al. Enabling search over encrypted multimedia databases[C]//Media Forensics and Security.[s.n.]:IEEE, 2009:7254. |
| [7] | Hsu C Y, Lu C S, P S C. Homomorphic encryption-based secure SIFT for privacy-preserving feature extraction[C]//Media Watermarking, Security, and Forensics Ⅲ.[s.n]:IEEE, 2011:7880. |
| [8] | Zhang X P. Reversible data hiding in encrypted image[J]. IEEE Signal Process. Lett., 2011, 18(4): 55–258. |
| [9] | Memon N, W P W. A buyer-seller watermarking protocol[J]. IEEE Trans. Image Process, 2011, 10(4): 643–649. |
| [10] | Tong SUN, Neuvo Y. Detail-preserving median based filters in image processing[J]. Pattern Recognit. Lett., 1994, 15: 341–347. DOI:10.1016/0167-8655(94)90082-5 |
| [11] | Wang Z, Zhang D. Progressive switching median filter for the removal of impulse noise from highly corrupted images[J]. IEEE Trans. Circuits Syst. Ⅱ, 1999, 46: 78–80. DOI:10.1109/82.749102 |
| [12] | Chen T, Ma K K, Chen L H. Tri-state median filter for image denoising[J]. IEEE Trans. Image Processing, 1999, 8: 1834–1838. DOI:10.1109/83.806630 |
| [13] | Zhang S Q, Mohanmmad A. A new impulse detector for switching median filters[J]. IEEE Trans. IEEE Signal Process, 2002, 9: 360–363. DOI:10.1109/LSP.2002.805310 |
| [14] | Akkul S, Ledee R, Leconge R, et al. A New Adaptive Switching Median Filter[J]. IEEE Signal Process, 2010, 17: 587–590. DOI:10.1109/LSP.2010.2048646 |
| [15] | Dong Y Q, Xu S F. A new directional weighted median filter for removal of random-value impulse noise[J]. IEEE Signal Process, 2007, 14: 193–196. DOI:10.1109/LSP.2006.884014 |
 2014, Vol. 37
2014, Vol. 37

