近年来全球气候问题逐渐加剧,政府间气候变化专门委员会的系列研究指出温室气体(尤其是CO2气体)的大量排放是主要影响因素之一[1-2],CO2减排已迫在眉睫。但是,作为CO2气体排放主要来源的化石燃料在能源供应中的地位在短期内仍无法改变[3],因此作为CO2减排的有效手段之一——CO2地质储存近年来受到了广泛关注。CO2地质储存的主要注入层包括产量下降和废弃的油气田,不可开采的煤层和深部咸水层[4]。将CO2注入油气储层,由于其具有附加的经济价值,是比较受欢迎的一种CO2地质储存方法,然而由于油气储层储存能力有限,单独采用该技术很难达到有效减少向大气排放CO2目的,而深部咸水层相比于其他类型的储层,具有分布广泛,储存潜力大等特点,是进行大量CO2储存的理想储层[1]。
大量注入CO2到深部咸水层会引起咸水层中的压力上升,压力上升的影响范围远远大于CO2运移的范围[5]。不同侧向范围的深部咸水层CO2注入后压力上升幅度不同,侧向范围大的提供了相对较大的空间来消散压力,压力上升幅度相对较小[6]。在盆地尺度进行CO2注入时,盆地边界相对CO2的注入来说往往表现“无限大”的特征[6-8]。在数值模拟过程中,给“无限大”的边界是不现实的,到底设置多大的边界范围和采用什么类型的边界才能刻画“无限大”的特征一直未能定量化分析。笔者首先基于数值模拟来分析边界范围和类型对CO2地质储存的影响,然后提出一种快速确定边界范围的方法。
1 模型的建立 1.1 模拟工具能用于CO2地质储存的数值模拟软件较多,例如COORES、ECLIPSE、GEM、STOMP和TOUGH系列等[9]。TOUGH系列由于其能够刻画多个过程和可信的模拟结果[10],被广泛用于CO2地质储存的研究中[11-13],其主要特征见表 1。
TOUGH2-MP[14]为并行版TOUGH2[15],能够进行上百万网格的模拟任务,与TOUGH2一样,其基于组分质量守恒和能量守恒求解多相流动过程中压力、饱和度、组分质量分数和温度的时空分布,采用的空间离散方法是积分有限差,时间离散是隐式差分,非线性方程求解是Newton-Raphson迭代,但其与TOUGH2的主要不同之处在于,在计算之前采用METIS进行网格的优化分割和基于并行求解器AZTEC的线性方程组求解。由于本文所建的网格数目较多,为了提高计算效率,采用TOUGH2-MP进行计算。
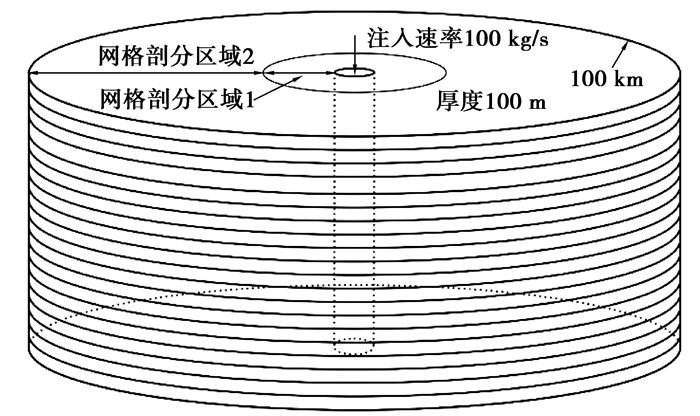
2.2 模型描述这里采用与Zhou[6]类似的二维径向深部咸水层模型(图 1),顶板埋深为1 200 m,厚度100 m,基本模型的径向长度是100 km,侧向边界类型为隔水边界,模型中相关参数见表 2。模型垂向上网格剖分间距为5 m,径向上井到150 m(剖分区域1)剖分间距为5 m,大于150 m(剖分区域2)剖分间距为50 m,基本模型网格总数为20×2 017=40 340。模型初始条件压力假设为静水压力,温度均为45 ℃,并在模拟中保持不变。CO2注入方式为定速率注入,注入速率为100 kg/s,注入时间和模拟时间均为30 a。
|
图 1 二维径向模型示意图 |
| 表 2 二维径向流动模拟储层基本物理参数 |
| 表 3 不同数值模拟方案的参数设置 |
CO2注入到咸水层中后的压力上升和CO2运移受边界大小、类型和咸水层渗透率、压缩系数、温度、盐度等多种因素的影响。为了分析这些影响,设计了3类数值模拟方案:1)Case2~Case4为不同边界范围情况;2)Case5为隔水边界和定压力边界2种情况;3)Case6~Case15为不同参数情况。
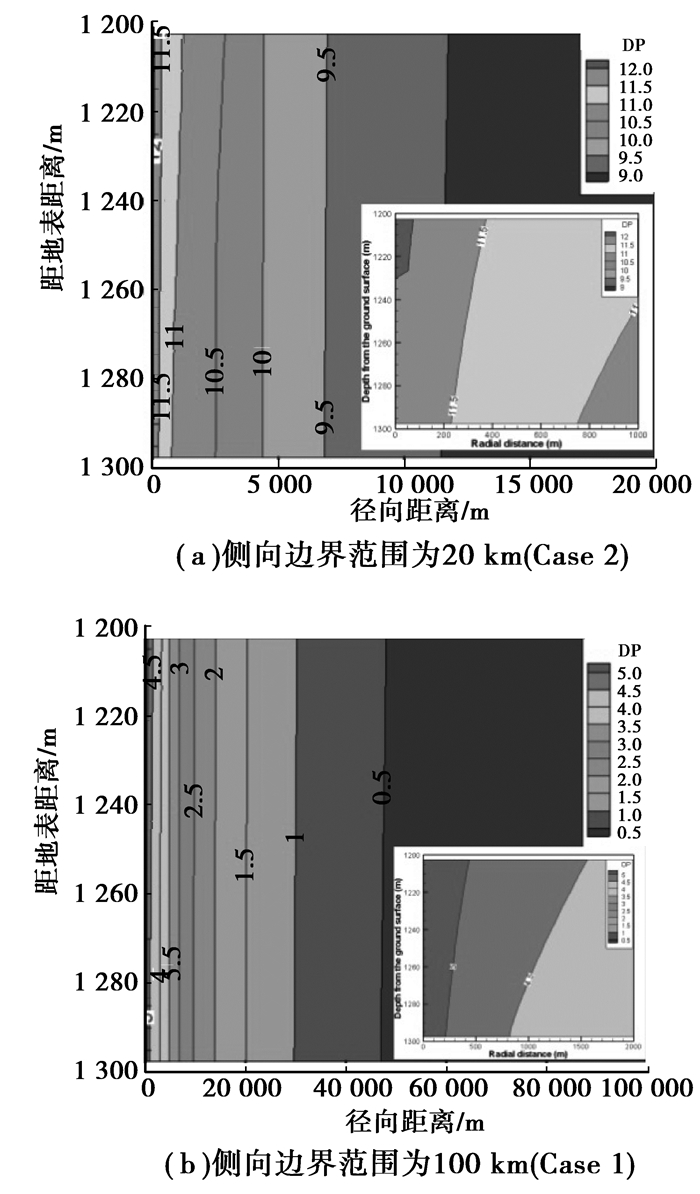
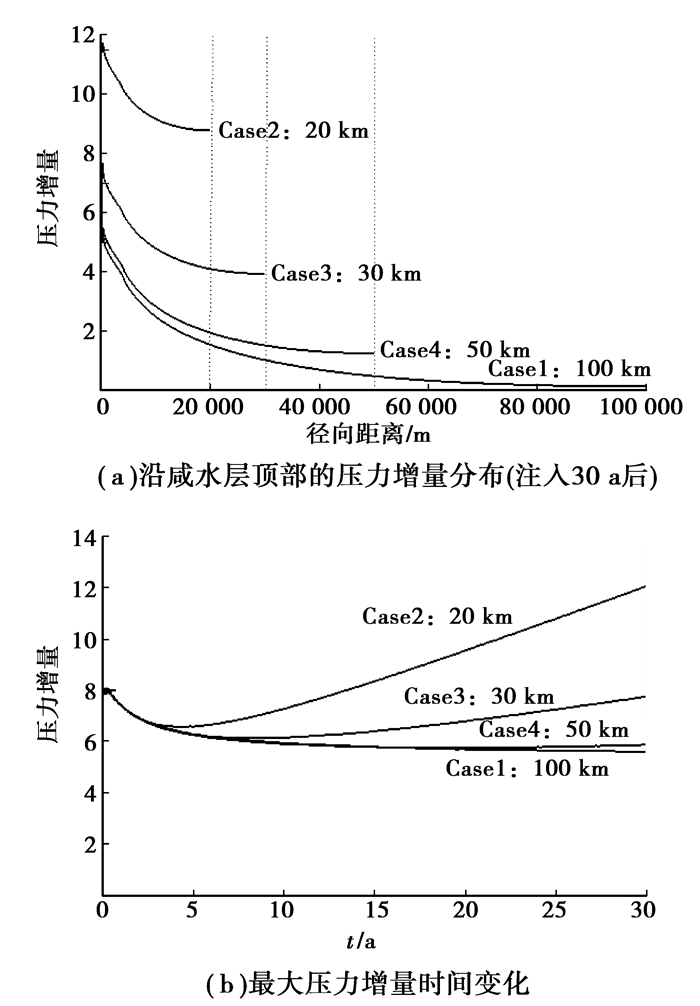
2 边界影响分析 2.1 边界对压力的影响从图 2、图 3可以看到,边界范围的大小对咸水层中的压力增量的时空分布特征有明显的影响。CO2注入以后咸水层中压力增加,整体上呈“活塞式”向外消散增加的压力,但由于CO2受地层水浮力的影响向上运动,并在盖层下聚集,导致在井附近顶部的压力增量大于底部。注入30 a后,压力增加的影响已经远远超过20 km范围,因此,20 km边界范围模型中的压力急剧上升,30 a后最外围的压力增量达到了9 MPa左右,井附近更高,接近13 MPa,若按照1.5倍静水压力设定为地层破坏条件[6],则地层早已破坏。图 3显示随着边界范围由20 km逐步增大到100 km时,压力的增加逐渐减小,这是因为咸水层有更大的空间进行压力消散。这种由于边界范围引起的压力增量随着边界范围的增大而逐渐减小的现象,在边界范围超过一定大小时(这里的模型近似为50 km),边界范围的影响可以忽略了。
|
图 2 CO2注入30 a后的压力增量空间分布(DP单位:MPa) |
|
图 3 不同侧向边界范围的压力增量特征 |
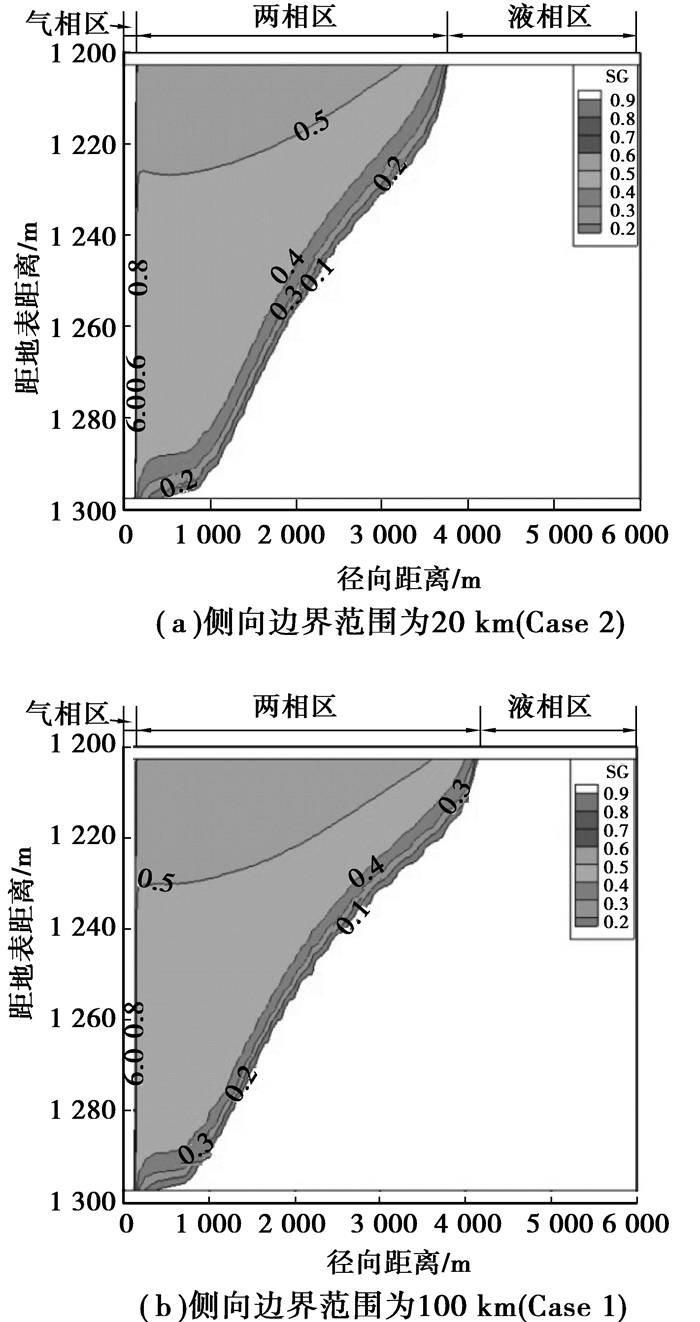
大量的CO2注入咸水层后产生明显的3个区域:气相(超临界)区、水-气两相区和液相区[16]。气相区分布在井筒附近,两相区域分布与气相饱和度分布类似,两相区域外为单相水区域(图 4)。可以看到,水气两相区和液相区占绝大部分区域。两相区域受边界范围大小设置的影响,边界范围大CO2运移的远,两相区域形状越扁平(图 4),最大CO2运移距离也大(图 5),20 km边界范围注入30 a后最大CO2运移距离约为3 600 m,而100 km则约为4 200 m。与对压力的影响类似,随着边界范围大小的增加,这种影响逐渐变小。
|
图 4 CO2注入30 a后的气体饱和度空间分布 |

|
图 5 CO2侧向最大运移距离时间变化 |
咸水层中注入的CO2主要以3种形式存在[1]:气相、溶解相和矿物相。由于水岩作用过程很慢,在注入时间尺度下,其对CO2的矿物捕获可以忽略。从表 4可以看到,边界范围对储存形式的影响并不大。虽然边界范围大的两相区域占据的范围大,CO2与地层水接触面也大,但是其压力增量变小,从而最终溶解CO2并不一定增加。在体积储存效率上(体积储存效率根据Okwen[17]定义为ε=Vinjected/Vformation=Qwellt/[φBπ(rmax)2],其中Qwell为注入速率,t为注入时间,φ为孔隙度,B为地层厚度,rmax为CO2侧向最大运移距离),边界范围小的明显要大一些,主要是因为其最大CO2运移距离小所致。因此,在边界范围小的情况下,“无限大”咸水层体积储存效率被高估。
| 表 4 不同边界范围的CO2储存形式 |
为了进一步探讨边界的影响与地层参数之间的关系,本文进行了渗透率、压缩系数、温度、盐度和边界类型的敏感性分析。
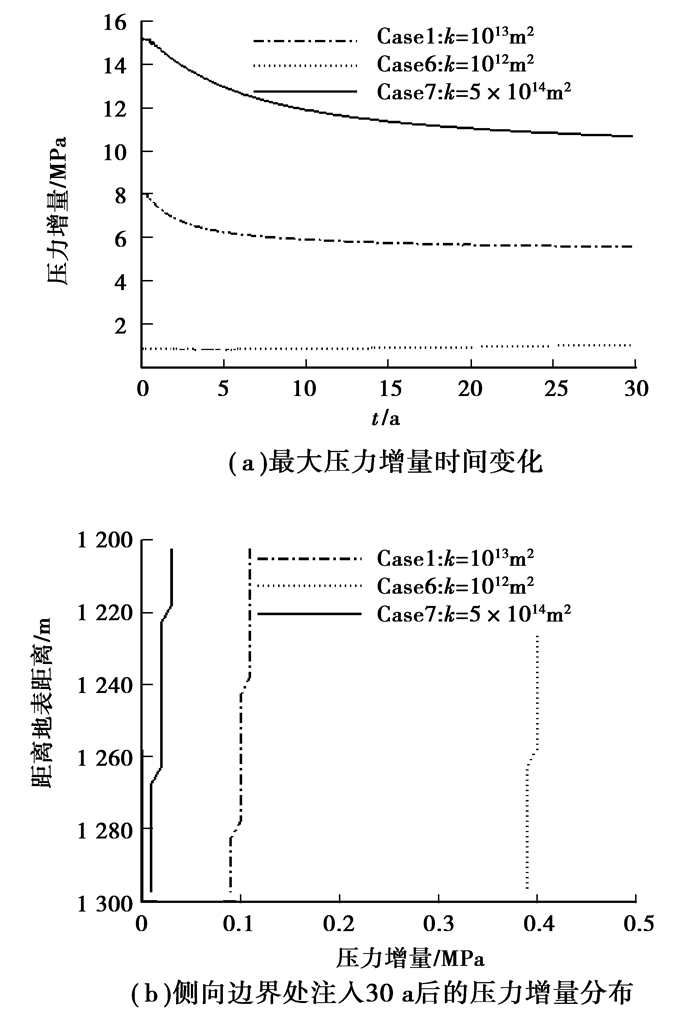
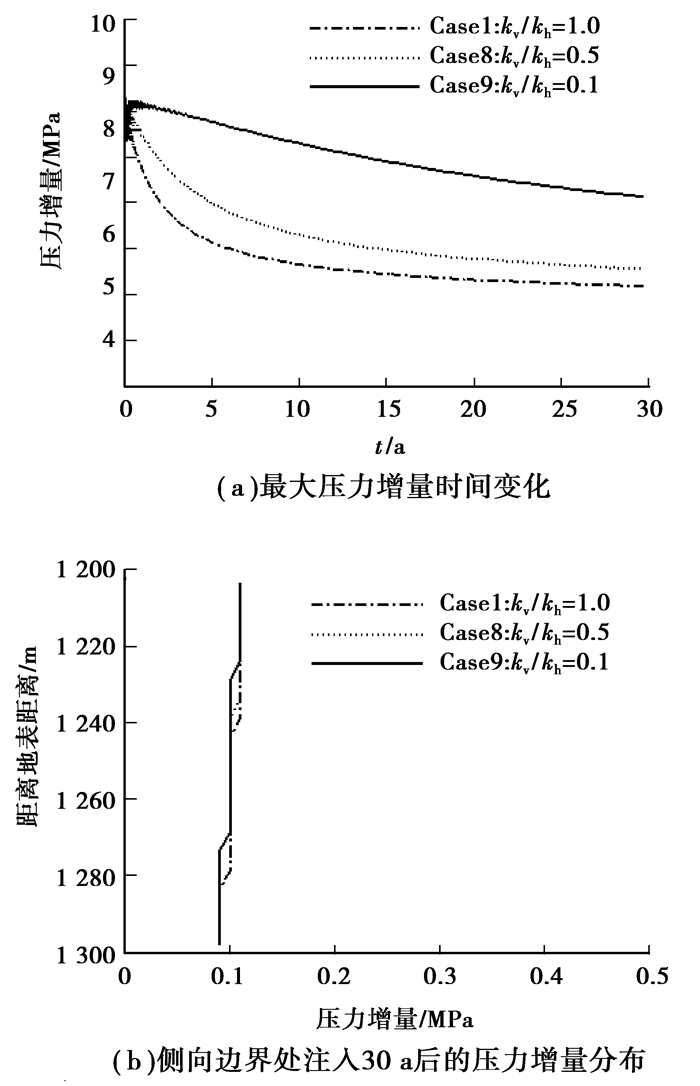
从图 6可以看到,渗透率大压力消散快,当然离井较远处的压力增量也大,即CO2注入导致的压力增量被更大范围咸水层来“平均”。因此,渗透率小CO2注入影响的范围小。垂直和水平渗透率的比值对井附近的压力有明显影响,比值小的压力增量越难于在垂直方向上消散,从而导致最大压力增量越大,但其对更远范围的压力影响不明显,因此,其对边界范围的影响不明显(图 7)。
|
图 6 地层渗透率对压力增量的影响 |
|
图 7 kh/kv对压力增量的影响 |
地层压缩系数大,单位压力下使得地层的变形就大,其用于储存的CO2空间也越大,那么,CO2注入引起的压力增量也就越小,注入影响范围也小(图 8)。

|
图 8 地层压缩系数对压力增量的影响 |
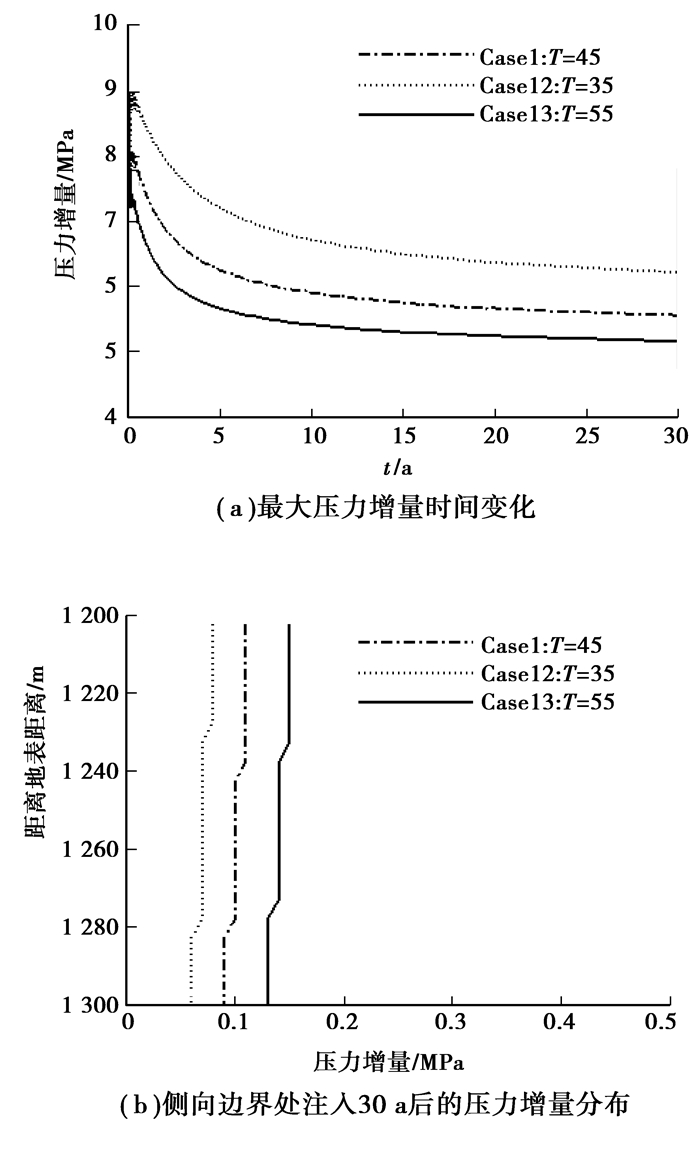
温度的影响比较复杂,它不仅影响CO2和地层水的属性(比如密度、黏度、焓等),并且还影响到CO2溶解过程,这些影响并不都是同方向的,哪种作用占主导取决于具体条件。就本文的参数条件而言,温度低不利于压力消散,即注入的影响范围相对较小(图 9)。
|
图 9 地层温度对压力增量的影响 |
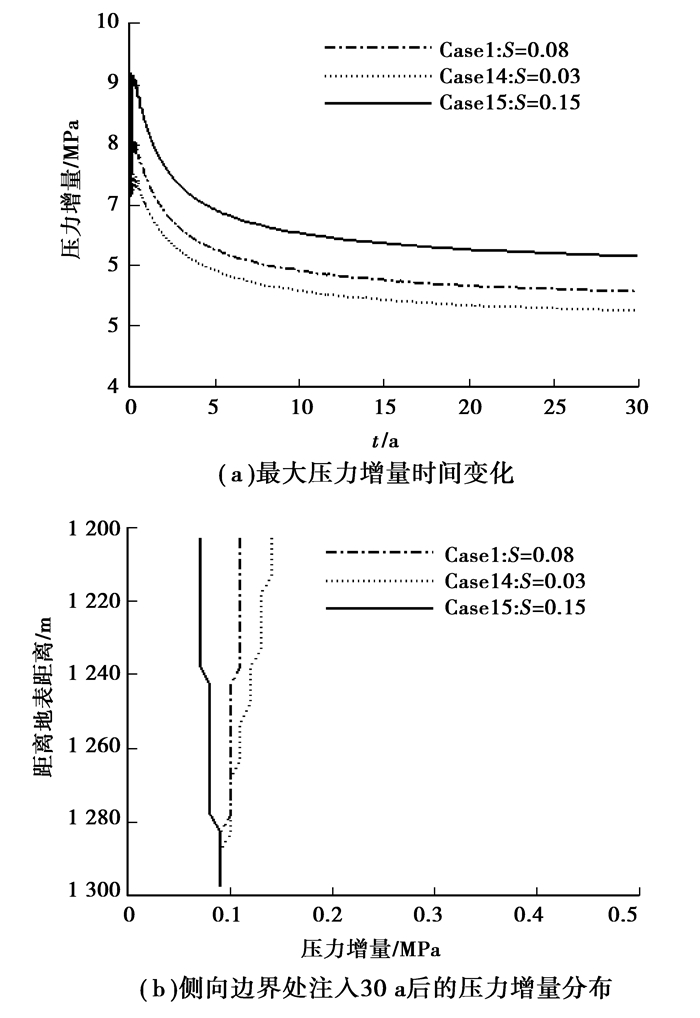
盐度增加会增大地层水的粘滞性,使得压力难于消散,但是,盐度大会影响到CO2向上运移过程,使得压力容易在地层下部聚集,从而,注入的影响范围上下是不一样的(图 10)。
|
图 10 地层水盐度对压力增量的影响 |
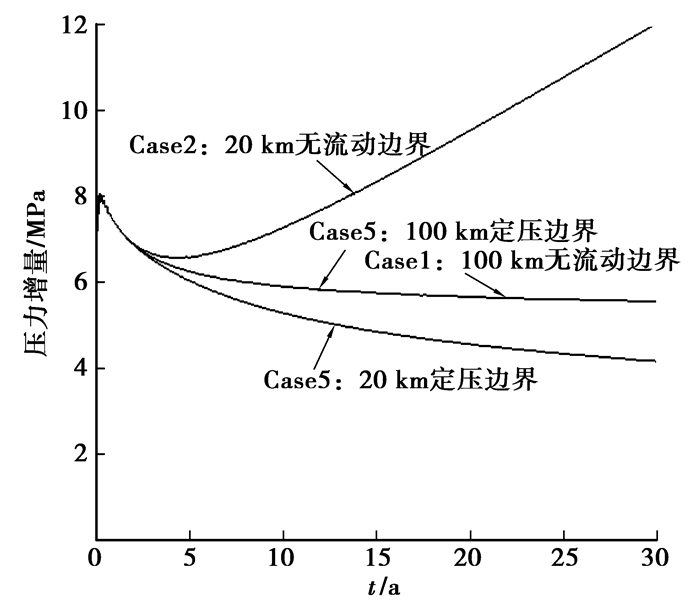
从图 11边界类型的模拟结果可以看到,在边界范围选择小时,定压边界优于隔水边界;当边界范围选择逐步增大,边界类型的影响越来越不明显。另外,采用小范围的定压边界时“无限大”咸水层中压力增量被低估。
|
图 11 边界类型对最大压力增量的影响 |
从各因素的影响对比分析,可以看到压缩系数和渗透率这两个因素对边界范围的确定影响比较大,因此,在边界范围的确定时应重点关注这两个参数。
3 边界确定方法 3.1 单井边界范围对于无限大或相对注入情况为无限大的咸水层,单井注入情况下可以采用单相Theis解析解[18]近似确定影响边界范围:
| $ P\left( {r, t} \right) - {P_{{\rm{int}}}} = \frac{{{Q_{{\rm{wel}}}}{\mu _{\rm{w}}}}}{{4{\rm{ \mathsf{ π} }}Mk}}W\left( u \right)。$ | (1) |
式中:P(r, t)为压力[ML-1T-2];Pint为初始压力[ML-1T-2];μw为黏度[ML-1T-1];k为渗透率[L2];M为厚度[L];W(u)为井函数,u=r2/(4at),a=k/[μw(βp+φβw)][M2/T],βp, βw分别为孔隙介质和流体压缩系数。
持续注入CO2引起压力的上升,“无限大”咸水层CO2地质储存数值模型中的影响边界可以定义为在注入过程中离井最近的压力上升为零的位置,该位置理论上并不存在,但可以假设上升压力足够小的位置为影响边界,足够小的标准假设取1%。因此,影响边界满足:
| $ \frac{{{Q_{{\rm{wel}}}}{\mu _{\rm{w}}}}}{{4{\rm{ \mathsf{ π} }}Mk}}W\left( {\frac{{r_{\rm{e}}^2}}{{4at}}} \right) = 0.01{P_{{\rm{int}}}}。$ | (2) |
CO2注入引起的压力上升为非稳定过程,因此影响边界随时间是变化的,数值模拟中应该根据持续注入时间来确定最大影响边界作为模型的边界。同时,边界范围还受多种因素的影响,比如温度、压力、盐度、岩石和水的压缩性等等。
考虑多相流动问题,影响边界范围需要加上二氧化碳的运移距离, 最大运移距离可通过下式计算[8, 16]:
| $ {r_{{\rm{max}}}} = \sqrt {\frac{{\lambda {Q_{{\rm{well}}}}t}}{{{\rm{ \mathsf{ π} }}M\varphi (1 - {S_{{\rm{lr}}}})}}} 。$ | (3) |
式中:二氧化碳和水的流动性比率λ=λc/λw,二氧化碳流动性λc=krc/μc,水的流动性λw=krw/μw;Slr为残余水饱和度。
根据式(2)、(3)可得数值模拟中二氧化碳的边界范围为:
| $ {R_\infty } = {r_{{\rm{max}}}} + {r_{\rm{e}}}。$ | (4) |
采用上面的方法对第二节中模型边界范围近似计算,其结果见表 5,从Case1可以看到,计算的影响边界约44 km,与数值模拟分析的近似50 km结果很吻合。
| 表 5 模型边界范围计算结果 |
从表 5可以看出,不同参数的影响边界不同,影响边界的主要贡献是水相的作用(re),而CO2的运移距离的贡献(rmax)不大且差别不大。影响边界随着渗透率、温度的增加而增大,而随着孔隙度、压缩系数和盐度的增加而减小。渗透率越大,压力传导的越远;孔隙度和地层压缩系数越大,可用于储存CO2的空间越大;温度主要通过影响流体参数(黏度、密度等)来影响边界,本文模型中呈现温度越高,影响边界越大,主要是因为密度变化大于其他的变化,从而影响注入体积的变化。盐度通过影响咸水的黏度影响re和rmax,但由于黏度差别不大,从而影响边界差别不大。
3.2 多井边界范围对于多井的边界范围可以通过叠加法确定re:
| $ \sum\limits_{i = 1}^n {\frac{{{Q_{{\rm{wel}}}}{\mu _{\rm{w}}}}}{{4{\rm{ \mathsf{ π} }}Mk}}} W\left( {\frac{{r_l^2}}{{4at}}} \right) = 0.01{P_{{\rm{int}}}}, $ | (5A) |
| $ {r_{\rm{l}}} = {({x_{\rm{e}}} - {x_i})^2} + {({y_{\rm{e}}} - {y_i})^2}, i = 1, 2, \ldots, n。$ | (5B) |
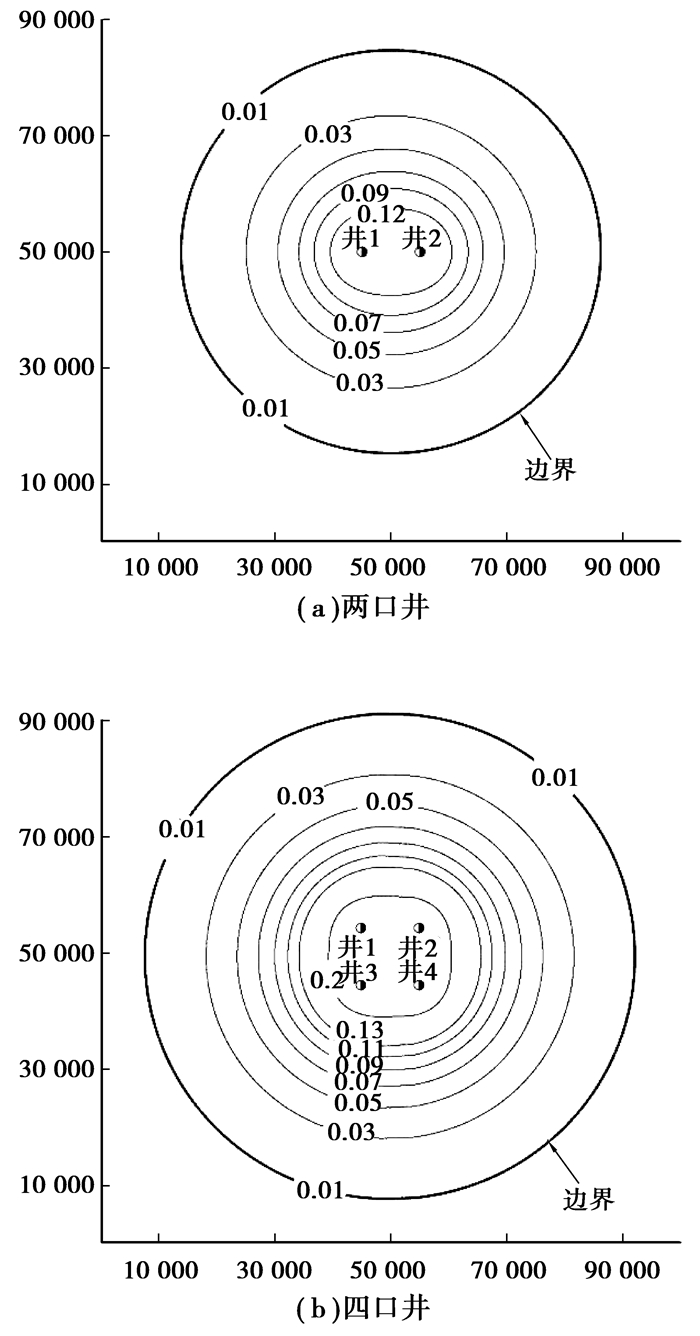
式中:rl为影响边界到井位置的距离[L];(xe, ye)和(xi, yi)分别为影响边界和井的位置坐标[L]。简单两口井和四口井注入影响边界计算效果见图 12。
|
图 12 多井注入的影响边界 (等值线为压力增加与初始压力的比值) |
以并行程序TOUGH2-MP为工具,通过二维径向模型边界影响的数值模拟研究,可以得到以下认识:
1)“无限大”深部咸水层大规模CO2的注入数值模拟研究中,人为设定的边界范围会影响到模拟结果,边界范围设定过小,表现不出深部咸水层的“无限大”行为,边界范围设定过大,会大大增加计算任务。
2) 边界范围影响压力和饱和度的时空分布,而对CO2的储存形式和体积储存效率影响不明显。CO2注入引起的压力增量是随着边界范围选择的增大而减小,气体饱和度分布是越扁平。边界范围选择大到一定程度后,无论是边界类型还是边界范围大小,其对CO2地质储存的影响可都以忽略。设定定压边界为侧向边界从某种程度上优于隔水边界,但是定压力边界范围设置的过小,会低估储层压力增量。
3) 渗透系数、地层压缩系数、温度和盐度影响CO2注入后的压力分布特征,从而影响空间范围大小不同。在渗透系数大、地层压缩系数小和温度大时,影响范围大,反之则小。因此,在进行模型边界设定时应予以考虑。
4) 基于单相Theis解析解和CO2最大运移距离,可以在模拟前近似快速确定侧向的边界范围。
本次研究结论是在特定参数条件下获得的,边界范围的影响仅从压力、CO2饱和度、储存形式和效率方面进行了分析,对其他变量的影响问题,还需在以后的研究中进一步深入。
| [1] | Intergovernmental Panel on Climate Change. Carbon Dioxide Capture and Storage[R]. UK and New York:Cambridge University Press, 2005. |
| [2] | Intergovernmental Panel on Climate Change. Climate change 2007:the physical science basis[R]. Fourth assessment report, Secretariat, Geneva, Switzerland:IPCC, 2007. |
| [3] | International Energy Agency(IEA). World Energy Ooutlook[EB/OL].[2013-09-23]. http://www.worldenergyoutlook.org/publications/weo-weo-2011/. |
| [4] | A global response to the challenge of climate change[R].[S.l.]:Carbon Sequestration Leadership Forum Technology Roadmap(CSLF), 2010. |
| [5] | Birkholzer J T, Zhou Q L, Tsang C F. Large-scale impact of CO2 storage in deep saline aquifer:a sensitivity study on pressure response in stratified systems[J]. International Journal of Greenhouse Gas Control, 2009, 3(2): 181–194. DOI:10.1016/j.ijggc.2008.08.002 |
| [6] | Zhou Q L, Birkholzer J T, Cappa F, et al. A method for quick assessment of CO2 storage capacity in closed and semi-closed saline formations[J]. International Journal of Greenhouse Gas Control, 2008, 2(4): 626–639. DOI:10.1016/j.ijggc.2008.02.004 |
| [7] | Wang Y, Xu Y, Zhang K. Investigation of CO2 storage capacity in open saline aquifers with numerical models[J]. Procedia Engineering, 2012, 31: 886–892. DOI:10.1016/j.proeng.2012.01.1117 |
| [8] | Nordbotten J M, Celia M A, Bachu S. Injection and storage of CO2 in deep saline aquifers:analytical solution for CO2 plume evolution during injection[J]. Transport in Porous Media, 2005, 58(3): 339–360. DOI:10.1007/s11242-004-0670-9 |
| [9] | Xi J. A review of physical modeling and numerical simulation of long-term geological storage of CO2[J]. Applied Energy, 2011, 88(11): 3557–3566. DOI:10.1016/j.apenergy.2011.05.004 |
| [10] | Pruess K, García J, Kovscek T, et al. Code intercomparison builds confidence in numerical simulation models for geological disposal of CO2[J]. Energy, 2004, 29(9/10): 1431–1444. |
| [11] | Pruess K, García J. Multiphase flow dynamics during CO2 disposal into saline aquifers[J]. Environmental Geology, 2002, 42(2/3): 282–295. |
| [12] | Xu T, Sonnenthal E, Spycher N, et al. TOUGHREACT-A simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geological media:Application to geothermal injectivity and CO2 geological sequestration[J]. Computers & Geosciences, 2006, 32(2): 145–165. |
| [13] | Rutqvist J, Wu Y S, Tsang C F, et al. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(4): 429–442. |
| [14] | Zhang K N, Wu Y S, Pruess K. User's Guider for TOUGH2-MP-A Massively Parallel Version of the TOUGH2 Code. Earth Science Division[M]. Berkeley:Lawrence Berkeley National Laboratory, University of California, 2008. |
| [15] | Pruess K, Curt O, George M. TOUGH2 USER'S GUIDE, VERSION 2.0. Earth Science Division[M]. Berkeley:Lawrence Berkeley National Laboratory, University of California, 1999. |
| [16] | Okwen R T, Stewart M T, Cunningham J A. Analytical model for screening potential CO2 repositories[J]. Computational Geosciences, 2011, 15(4): 755–770. DOI:10.1007/s10596-011-9246-2 |
| [17] | Okwen R T, Stewart M T, Cunningham J A. Analytical solution for estimation storage efficiency of geologic sequestration of CO2[J]. International Journal of Greenhouse Gas Control, 2010, 4(1): 102–107. DOI:10.1016/j.ijggc.2009.11.002 |
| [18] | Theis C V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage[M]. Washington D C: Transactions of the American Geophysical Union 16, 1935: 519-524. |
 2014, Vol. 37
2014, Vol. 37


