收稿日期: 2013-10-20
基金项目: 国家自然科学基金资助项目(51005255);教育部高等学校博士学科点科研基金项目(20090191120005)
Infulence of individual pitch control on the load of large-scale wind turbine
College of Mechanicd Engineering, Chongqing University, Chongqing 400044, China
随着能源及环境形势越来越严峻,世界各国都在大力发展清洁的可再生能源。风能的利用在近几年有突飞猛进的增长,而这离不开很多机构和个人在科研上做出的努力。所有的研究只有一个目的:降低利用风能的成本。降低成本的策略有很多,其中包括研制大型的风力机。目前3 MW商业风机的风轮直径达110 m,5 MW的风轮直径为126 m[1-3]。风机尺寸的增大意味着转子直径和转子扫掠面积也要相对增大,这导致整个扫掠面积内不均衡的风场,并进而使叶片、驱动轴以及风机结构之间载荷不均。不均衡的载荷会加速部件磨损,降低发电效率,并延长所需要的维护停机时间。这一切可通过设计采用独立变桨控制(IPC)的桨距控制系统来克服。
独立变桨最初用于直升机上,Johnson和Lovera在这个领域做了大量研究。随后被很多学者引入到风机的控制中。Larsen采用的周期变桨控制可有效减轻一阶旋转频率引起的载荷。Wright引入状态空间方法来抵消风剪导致的载荷,效果仍仅限于一阶频率。周期变桨控制不能减轻风的随机湍流导致的载荷,鉴于此,Bossanyi和Larsen的方法是通过测量获得叶根载荷的平均值,并将其解耦到2个相互垂直的坐标系上,这样就能采用传统的单输入单输出控制方法。近年来,国外风电巨头Vestas、GE、三菱、Gamesa都对风力发电机的独立变桨技术进行了研究,并拟在将来用于工程实际中。国外对独立变桨展开研究较早[4-9],然而国内对独立变桨控制技术的研究尚处于起步阶段[10-11]。
以大型风力发电机组为研究对象,在建立风力发电机空气动力学模型的基础上,建立系统状态空间方程,对其进行独立变桨控制设计理论研究,采用MATLAB/SIMULINK实现控制器的编程,分析结果与统一变桨比较,证明了所建立控制模型的有效性,研究结果对大型风力发电机组的进一步优化设计、优化控制等均具有指导意义。
1 线性空气动力学计算模型
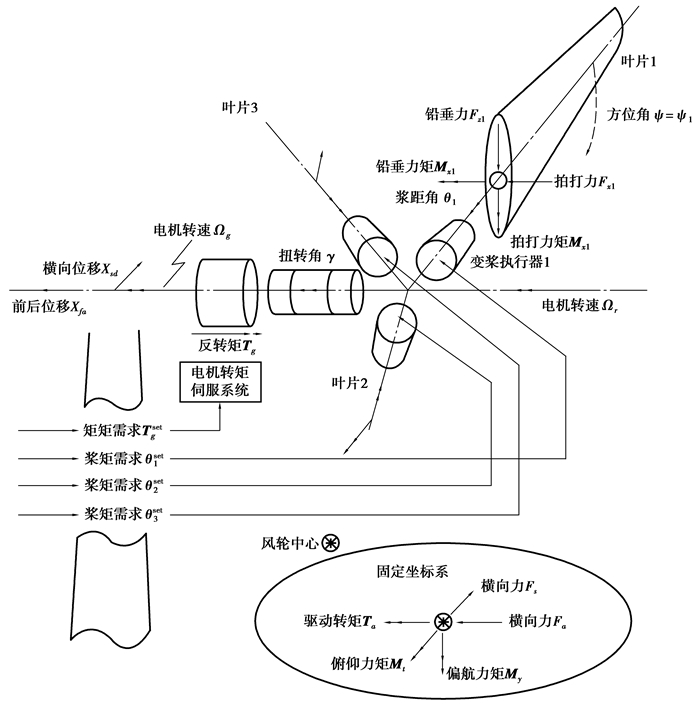
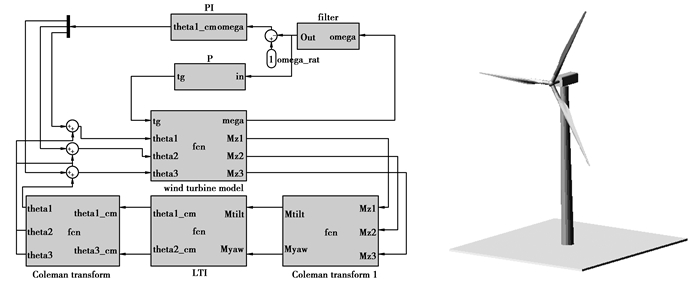
独立变桨控制的目的是保证风力发电机空气动力学性能稳定,控制的对象是转矩、力和力矩,因此有必要先建立线性空气动力学计算模型。模型框图如图 1所示。
采用线性的叶素动量理论将叶片拍打方向的相对风速变化转换为叶片所受的力和力矩(叶根拍打方向和挥舞方向的力矩)的变化。空气动力学模型本质上是将拍打方向的相对风速转换为叶根所受的拍打和挥舞方向的力和力矩。第i个叶片所受的力和力矩与桨距角的变化θi,相对风速vfli的关系见公式(1)。
|
$
\left. \begin{array}{l}
\delta {\mathit{\boldsymbol{M}}_{z,i}} = {h_{{\mathit{\boldsymbol{M}}_z}}}{\upsilon _{fli}} + {k_{{\mathit{\boldsymbol{M}}_z}}}{\theta _i}\\
\delta {F_{x,i}} = {h_{{F_z}}}{\upsilon _{fli}} + {k_{{F_x}}}{\theta _i}\\
\delta {\mathit{\boldsymbol{M}}_{x,i}} = {h_{{\mathit{\boldsymbol{M}}_x}}}{\upsilon _{fli}} + {k_{{\mathit{\boldsymbol{M}}_x}}}{\theta _i}\\
\delta {F_{z,i}} = {h_{{F_z}}}{\upsilon _{fli}} + {k_{{F_z}}}{\theta _i}
\end{array} \right\},
$
|
(1) |
对于风轮气动力矩的变化δTa,轴向力变化δFa,倾覆力矩变化δMt和侧向力变化δFs,见式(2)
|
$
\begin{array}{*{20}{c}}
{\delta {\mathit{\boldsymbol{T}}_a} = \sum\limits_{i = 1}^B {\delta {\mathit{\boldsymbol{M}}_{{x_i}}}} ;\delta {F_a} = \sum\limits_{i = 1}^B {\delta {F_{{x_i}}}} ;}\\
{\delta {\mathit{\boldsymbol{M}}_t} = \sum\limits_{i = 1}^B {\sin {\psi _i}\delta {\mathit{\boldsymbol{M}}_{{z_i}}}} ;\delta {F_s} = \sum\limits_{i = 1}^B {\sin {\psi _i}\delta {F_{{z_i}}}} 。}
\end{array}
$
|
(2) |
第i个叶片拍打方向的相对风速变化vfli是叶片有效风速${\tilde u_i}$与风轮沿风向运动速度的叠加。后者由塔架前后方向的弯曲造成的(假定叶片完全刚性)。迎风结构的运动包括塔顶前后移动速度${\dot x_{fa}}$和俯仰转动速度${\dot \varphi _{fa}}$。后者对相对风速的影响与风轮所处方位角有关,并沿风轮径向变化。取风轮径向占叶片长度3/4处(3Rb/4)作为的受影响点,以考虑${\dot \varphi _{fa}}$对叶片载荷的影响[12-13]。因此,拍打方向的相对风速vfli可由式(3)得出
|
$
{\upsilon _{f{l_i}}} = {{\tilde u}_i} - \dot x{f_a} + \sin \left( {{\psi _i}} \right)\frac{3}{{2H}}\frac{{3{R_b}}}{4}{{\dot x}_{fa}},
$
|
(3) |
其中,系数3/2H是长度为H的等截面梁承受弯曲载荷时位移与转角的比值。
|
$
{\psi _1} = \psi ;{\psi _2} = \psi + \frac{{2{\rm{ \mathsf{ π} }}}}{3};{\psi _3} = \psi + \frac{{4{\rm{ \mathsf{ π} }}}}{3},
$
|
(4) |
其中,hMz… kFz由所选工作点的功率系数和推力系数求导得出,与风速、风轮转速及桨距角有关。
2 系统状态空间方程建立
由于风轮的周期旋转,在线性化过程中使用Coleman变换进行转换。与方位角(ψ)有关的运动方程除了风轮转速以外,不包含风轮的叶片和轴上其他的状态变量(另外2个状态变量是塔架前后位移xfa和侧向位移xsd)。由于存在同轴方向,Coleman变换对转速Ω没有影响,所以不必将所有的变量进行Coleman变换。拍打方向的弯矩,桨距角和叶片上有效风速使用Coleman变换矩阵P进行变换。Coleman矩阵P能够将叶片旋转坐标系p转换为多叶片坐标系pcm。线性模型描述如下
|
$
J \cdot \mathit{\dot \Omega = } - 3{h_{{\mathit{\boldsymbol{M}}_x}}}{{\dot x}_{fa}} + 3{k_{{\mathit{\boldsymbol{M}}_x}}}\theta _1^{cm} + 3{h_{{\mathit{\boldsymbol{M}}_x}}}\tilde u_1^{cm} - \delta {\mathit{\boldsymbol{T}}_g},
$
|
(5) |
|
$
\begin{array}{*{20}{c}}
{{m_{tw}} \cdot {{\ddot{x}}_{fa}} = - {s_{tw}}{x_{fa}} - \left( {{d_{tw}} + 3{h_{{F_x}}} - \frac{{81{R_b}}}{{32{H^2}}}{h_{{\mathit{\boldsymbol{M}}_x}}}} \right){{\dot x}_{fa}} + }\\
{3{k_{{F_x}}}\theta _1^{cm} + \frac{9}{{4H}}{k_{{\mathit{\boldsymbol{M}}_z}}}\theta _2^{cm} + 3{h_{{F_x}}}\tilde u_1^{cm} + \frac{9}{{4H}}{h_{{\mathit{\boldsymbol{M}}_z}}}\tilde u_2^{cm}。}
\end{array}
$
|
(6) |
|
$
\begin{array}{*{20}{c}}
{{m_{tw}} \cdot {{\ddot x}_{sd}} = \frac{3}{{2H}}\delta {T_g} - \frac{{27{R_b}}}{{16{H^2}}}{h_{{F_z}}}{{\dot x}_{fa}} - }\\
{\frac{3}{2}{k_{{F_z}}}\theta _2^{cm} - \frac{3}{2}{h_{{F_z}}}\tilde u_2^{cm} - {s_{tw}}{x_{sd}} - {d_{tw}}{{\dot x}_{sd}},}
\end{array}
$
|
(7) |
|
$
\delta {\mathit{\boldsymbol{M}}_{{\rm{zcml}}}} = - {h_{{\mathit{\boldsymbol{M}}_z}}}{{\dot x}_{fa}} + {k_{{\mathit{\boldsymbol{M}}_z}}}\theta _1^{cm} + {h_{{\mathit{\boldsymbol{M}}_z}}}\tilde u_1^{cm},
$
|
(8) |
|
$
\delta {\mathit{\boldsymbol{M}}_{{\rm{tilt}}}} = - {h_{{\mathit{\boldsymbol{M}}_z}}}\frac{{27{R_b}}}{{16H}}{{\dot x}_{fa}} - \frac{3}{2}{k_{{\mathit{\boldsymbol{M}}_z}}}\theta _2^{cm} - \frac{3}{2}{h_{{\mathit{\boldsymbol{M}}_z}}}\tilde u_2^{cm},
$
|
(9) |
|
$
\delta {\mathit{\boldsymbol{M}}_{{\rm{yaw}}}} = \frac{3}{2}{k_{{\mathit{\boldsymbol{M}}_z}}}\theta _3^{cm} + \frac{3}{2}{h_{{\mathit{\boldsymbol{M}}_z}}}\tilde u_3^{cm},
$
|
(10) |
式中:xfa为塔架的前后方向位移,xsd为侧向位移;Tg为发电机转矩,stw为塔架的弹性系数,dtw为塔架的阻尼系数;ucm为Coleman坐标系下风速。
为了实现控制器,将系统写成状态空间的形式,得到如下的状态空间模型公式(11)、(12)
|
$
\begin{array}{*{20}{c}}
{\left( {\begin{array}{*{20}{c}}
{\mathit{\dot \Omega }}\\
{{{\dot x}_{fa}}}\\
{{{\ddot x}_{fa}}}\\
{{{\dot x}_{sd}}}\\
{{{\ddot x}_{sd}}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
0&0&{\frac{{ - 3{h_{{\mathit{\boldsymbol{M}}_z}}}}}{J}}&0&0\\
0&0&1&0&0\\
0&{ - \frac{{{s_{tw}}}}{{{m_{tw}}}}}&{ - \frac{{\left( {{d_{tw}} + 3h\left( {{F_x}} \right) - \frac{{81{r_b}}}{{32{H^2}}}{h_{{\mathit{\boldsymbol{M}}_z}}}} \right)}}{{{m_{tw}}}}}&0&0\\
0&0&0&0&1\\
0&0&{ - \frac{{27{R_b}{h_{{F_z}}}}}{{16H{m_{tw}}}}}&{ - \frac{{{s_{tw}}}}{{{m_{tw}}}}}&{ - \frac{{{d_{tw}}}}{{{m_{tw}}}}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
\mathit{\Omega }\\
{{x_{fa}}}\\
{{{\dot x}_{fa}}}\\
{{x_{sd}}}\\
{{{\dot x}_{sd}}}
\end{array}} \right) + }\\
{\left( {\begin{array}{*{20}{c}}
{\frac{{3{h_{{\mathit{\boldsymbol{M}}_z}}}}}{J}}&0&0&{\frac{{3{k_{{\mathit{\boldsymbol{M}}_x}}}}}{J}}&0&0&{ - \frac{1}{J}}\\
0&0&0&0&0&0&0\\
{\frac{{3{h_{{F_x}}}}}{{{m_{tw}}}}}&{\frac{{\frac{9}{{4H}}{h_{{\mathit{\boldsymbol{M}}_z}}}}}{{{m_{tw}}}}}&0&{\frac{{3{k_{{F_x}}}}}{{{m_{tw}}}}}&{\frac{{\frac{9}{{4H}}{k_{{\mathit{\boldsymbol{M}}_z}}}}}{{{m_{tw}}}}}&0&0\\
0&0&0&0&0&0&0\\
0&{\frac{{\frac{3}{2}{h_{{F_z}}}}}{{{m_{tw}}}}}&0&0&{\frac{{\frac{3}{2}{k_{{F_z}}}}}{{{m_{tw}}}}}&0&{\frac{{\frac{3}{{2H}}}}{{{m_{tw}}}}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{\tilde u_1^{cm}}\\
{\tilde u_2^{cm}}\\
{\tilde u_3^{cm}}\\
{\theta _1^{cm}}\\
{\theta _2^{cm}}\\
{\theta _3^{cm}}\\
{\delta {T_g}}
\end{array}} \right),}
\end{array}
$
|
(11) |
|
$
\left( {\begin{array}{*{20}{c}}
\mathit{\Omega }\\
{\delta {\mathit{\boldsymbol{M}}_{zcm1}}}\\
{\delta {\mathit{\boldsymbol{M}}_{{\rm{tilt}}}}}\\
{\delta {\mathit{\boldsymbol{M}}_{{\rm{yaw}}}}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1&0&0&0&0\\
0&0&{ - {h_{{\mathit{\boldsymbol{M}}_z}}}}&0&0\\
0&0&{ - \frac{{27{R_b}}}{{16H}}{h_{{\mathit{\boldsymbol{M}}_z}}}}&0&0\\
0&0&0&0&0
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
\mathit{\Omega }\\
{{x_{fa}}}\\
{{{\dot x}_{fa}}}\\
{{x_{sd}}}\\
{{{\dot x}_{sd}}}
\end{array}} \right) +\\ \left( {\begin{array}{*{20}{c}}
0&0&0&0&0&0&0\\
{{h_{{\mathit{\boldsymbol{M}}_z}}}}&0&0&{{k_{{\mathit{\boldsymbol{M}}_z}}}}&0&0&0\\
0&{ - \frac{3}{2}{h_{{\mathit{\boldsymbol{M}}_z}}}}&0&0&{ - \frac{3}{2}{k_{{\mathit{\boldsymbol{M}}_z}}}}&0&0\\
0&0&{\frac{3}{2}{h_{{\mathit{\boldsymbol{M}}_z}}}}&0&0&{\frac{3}{2}{k_{{\mathit{\boldsymbol{M}}_z}}}}&0
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{\tilde u_1^{cm}}\\
{\tilde u_2^{cm}}\\
{\tilde u_3^{cm}}\\
{\theta _1^{cm}}\\
{\theta _2^{cm}}\\
{\theta _3^{cm}}\\
{\delta {T_g}}
\end{array}} \right)。$
|
(12) |
3 独立变桨控制器设计
为了便于独立变桨控制设计,风力发电机状态空间模型简化为公式(13)
|
$
\begin{array}{l}
{x^{wt}}\left( {k + 1} \right) = {A_{wt}}{x^{wt}}\left( k \right) + B_{wt}^\theta {\theta _{cm}}\left( k \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;B_{wt}^u{u_{cm}}\left( k \right) + \omega \left( k \right);\\
{y^{wt}}\left( k \right) = {C_{wt}}{x^{wt}}\left( k \right) + D_{wt}^\theta {\theta _{cm}}\left( k \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;D_{wt}^u{u_{cm}}\left( k \right) + \upsilon \left( k \right)。\end{array}
$
|
(13) |
输入风速信号见公式(14)
|
$
\begin{array}{*{20}{c}}
{z\left( {k + 1} \right) = {\Phi _z}\left( k \right) + {\omega _z}\left( k \right);}\\
{{u_{cm}}\left( k \right) = {\Gamma _z}\left( k \right)。}
\end{array}
$
|
(14) |
由式(13),(14)获得扩展的状态空间模型,见公式(15)。
|
$
\begin{array}{*{20}{c}}
{\left( {\begin{array}{*{20}{c}}
{{x^{wt}}\left( {k + 1} \right)}\\
{z\left( {k + 1} \right)}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{{A_{wt}}}&{B_{wt}^u\Gamma }\\
0&\Phi
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{{x^{wt}}\left( k \right)}\\
{z\left( k \right)}
\end{array}} \right) + }\\
{\left( {\begin{array}{*{20}{c}}
{B_{wt}^\theta }\\
0
\end{array}} \right){\theta _{cm}}\left( k \right) + \left( {\begin{array}{*{20}{c}}
{\omega \left( k \right)}\\
{{\omega _z}\left( k \right)}
\end{array}} \right),}\\
{{y^{wt}}\left( k \right) = \left( {{C_{wt}}\left( 0 \right)\left( {\begin{array}{*{20}{c}}
{{x^{wt}}\left( k \right)}\\
{z\left( k \right)}
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
{D_{wt}^\theta }\\
0
\end{array}} \right){\theta _{cm}}\left( k \right) + \upsilon \left( k \right)} \right.。}
\end{array}
$
|
(15) |
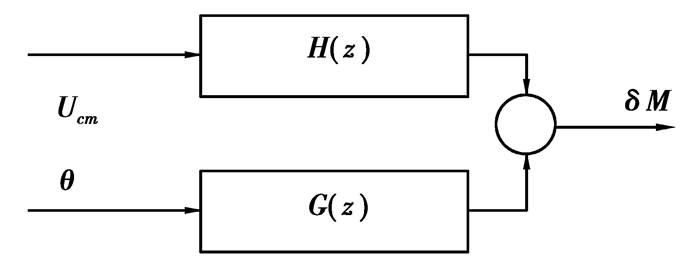
风力发电系统中确定叶片载荷的子系统可由两个传递函数给出。其中一个由变桨导致的叶片载荷,另一个由风速引起的载荷,如图 2所示。
考虑桨距角到叶片载荷的传递函数,写成状态空间如式(16)所示。
|
$
\begin{array}{*{20}{c}}
{{x^{wt}}\left( {k + 1} \right) = A{x^{wt}}\left( k \right) + B_{wt}^\theta {\theta _{cm}}\left( k \right) + \omega \left( k \right);}\\
{{y^{wt}}\left( k \right) = {C_{wt}}{x^{wt}}\left( k \right) + D_{wt}^\theta {\theta _{cm}}\left( k \right) + \upsilon \left( k \right)。}
\end{array}
$
|
(16) |
其增益通过采用反馈约束条件θcm(k)=-Kx(K)决定的。见公式(17)。
|
$
J = \sum\limits_{k = 0}^\infty {x\left( k \right)w{\mathit{\boldsymbol{t}}^{\rm{T}}}Qx\left( k \right)wt + {\mathit{\boldsymbol{\theta }}_{cm}}{{\left( k \right)}^{\rm{T}}}R{\mathit{\boldsymbol{\theta }}_{cm}}\left( k \right)} 。$
|
(17) |
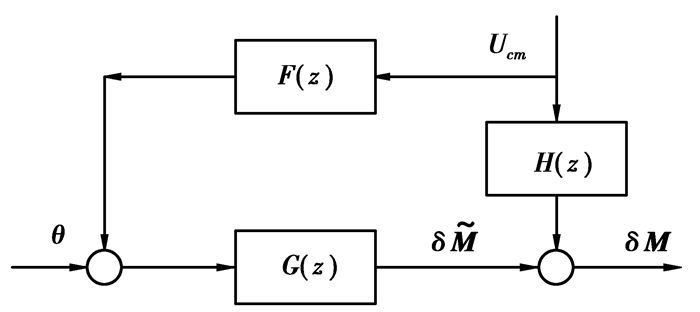
为减小由于风的扰动引起的载荷,引入前馈机制。根据卡尔曼滤波器估计的无偏差风速设计风速前馈控制器。如图 3所示,控制器(F(z))用来减小风速扰动的前馈控制器。
模型使用静态增益来模拟动态的风速前馈控制过程。由于偏航分量对风机的状态没有影响,风速前馈补偿增益也是个固定值,使控制器的设计更简单。因而补偿俯仰力矩的前馈增益可由下式计算
|
$
\delta {\mathit{\boldsymbol{M}}_{{\rm{tilt}}}} = - {h_{{\mathit{\boldsymbol{M}}_z}}}\frac{{27{R_b}}}{{16H}}{{\dot x}_{fa}} - \frac{3}{2}{k_{{\mathit{\boldsymbol{M}}_z}}}\theta _2^{cm} - \frac{3}{2}{h_{{\mathit{\boldsymbol{M}}_z}}}\tilde u_2^{cm},
$
|
(18) |
对于前馈控制器,需要补偿风速扰动引起的载荷。理想的前馈增益能将由$\tilde u_2^{cm}$引起的δMtilt减小为零。所以有下式
|
$
\theta _2^{cm} = - \frac{{{h_{{M_z}}}}}{{{k_{{M_z}}}}}\tilde u_2^{cm}。$
|
(19) |
采用相同的方法计算偏航力矩(δMyaw)的前馈增益。从公式(10)可知偏航力矩取决于桨距角和风所产生载荷的偏航分量。因此有
|
$
\theta _3^{cm} = - \frac{{{h_{{\mathit{\boldsymbol{M}}_z}}}}}{{{k_{{\mathit{\boldsymbol{M}}_z}}}}}\tilde u_3^{cm}。$
|
(20) |
反馈环的功能为:1)在系统的设定点,采用一个PI补偿器建立低通滤波后的转速Ωg和统一变桨角θ的关系,并且通过风速前馈来考虑动态入流的影响。2)采用卡尔曼滤波器设计的LQG控制器及上述的最优增益,将低通滤波后的俯仰和偏航方向的多叶片拍打坐标系上的力矩转换到俯仰和偏航方向的多叶片变桨力矩坐标系上。对于后一项功能,采用如下式对δMzcm2和δMzcm3虚拟测量
|
$
\left( {\begin{array}{*{20}{c}}
{\delta {\mathit{\boldsymbol{M}}_{zcm2}}}\\
{\delta {\mathit{\boldsymbol{M}}_{zcm3}}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{\frac{2}{3}\sin \psi 1}&{\frac{2}{3}\sin \psi 2}&{\frac{2}{3}\sin \psi 3}\\
{\frac{2}{3}\cos \psi 1}&{\frac{2}{3}\cos \psi 2}&{\frac{2}{3}\cos \psi 3}
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{\delta {\mathit{\boldsymbol{M}}_{z1}}}\\
{\delta {\mathit{\boldsymbol{M}}_{z2}}}\\
{\delta {\mathit{\boldsymbol{M}}_{z3}}}
\end{array}} \right)。$
|
(21) |
桨距角则使用如下的调制方法从控制信号θ2cm和θ3cm得到,见公式(22)
|
$
\left( {\begin{array}{*{20}{c}}
{{\theta _1}}\\
{{\theta _2}}\\
{{\theta _3}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{\sin \psi 1}&{\cos \psi 1}\\
{\sin \psi 2}&{\cos \psi 2}\\
{\sin \psi 3}&{\cos \psi 3}
\end{array}} \right) \cdot \left( \begin{array}{l}
\theta _2^{cm}\\
\theta _3^{cm}
\end{array} \right)。$
|
(22) |
测得的电机转速需经过低通滤波以排除高频干扰,根据实际风机参数,角频率设为0.25 Hz。风机在变桨的过程中通过变桨伺服电机将桨距需求转换成实际的桨距角。根据某企业实际风机的参数,设置桨距角的位置限制为0~90°,速率限制为-8~+8 deg/s。桨距角输出之前需通过位置和速率的饱和,以确保桨距角不超过执行器的变桨能力。
为了实现独立变桨控制策略,采用MATLAB/SIMULINK实现控制器的编程,同时为了结合控制器和风力发电机一起分析,使用ADAMS进行风力发电机的结构动力学计算,图 4是风力发电机独立变桨分析模型。
4 仿真实验
算例采用2 MW变速恒频风力机进行仿真,基本结构采用三叶片上风向,叶轮直径77.5 m,叶片长度38.75 m,轮毂高度为60 m,机组主要参数如表 1所示。2 MW独立变桨设计控制需要参数见表 2。
表 1(Table 1)
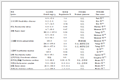
表 1 2MW风力发电机组主要参数
| 额定功率 |
2 MW |
| 叶片长度 |
38.75 m |
| 风轮直径 |
80 m |
| 塔架高度 |
60 m |
| 齿轮箱传动比 |
117 |
| 额定转速 |
15 r/min |
| 最小变桨角 |
0° |
| 最大变桨角 |
30° |
| 发电机额定转速 |
1 755 r/min |
| 发电机额定转矩 |
12 385.6 Nm |
|
表 1 2MW风力发电机组主要参数
|
表 2(Table 2)

表 2 2MW独立变桨设计控制需要参数
| 符号 |
数值 |
单位 |
| hFX |
5.76×103 |
N/(m·s-1) |
| hMX |
6.70×104 |
(Nm)/(m·s-1) |
| hFZ |
3.25×103 |
N/(m·s-1) |
| hMZ |
-1.52×105 |
(Nm)/(m·s-1) |
| kFX |
-4.92×103 |
N/(°) |
| kMX |
-3.02×104 |
(Nm)/(°) |
| kFZ |
-1.46×103 |
N/(°) |
| kMZ |
1.29×105 |
(Nm)/(°) |
|
表 2 2MW独立变桨设计控制需要参数
|
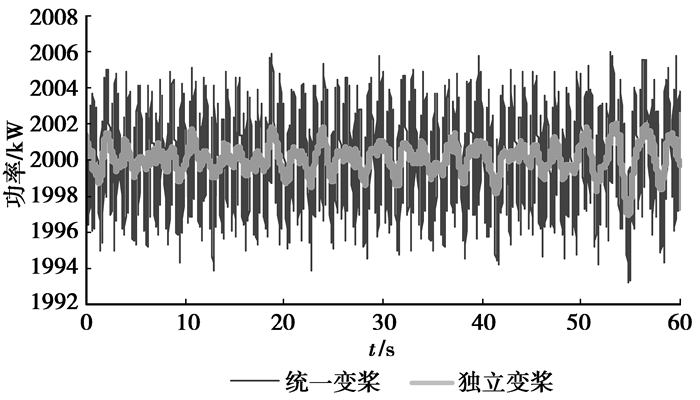
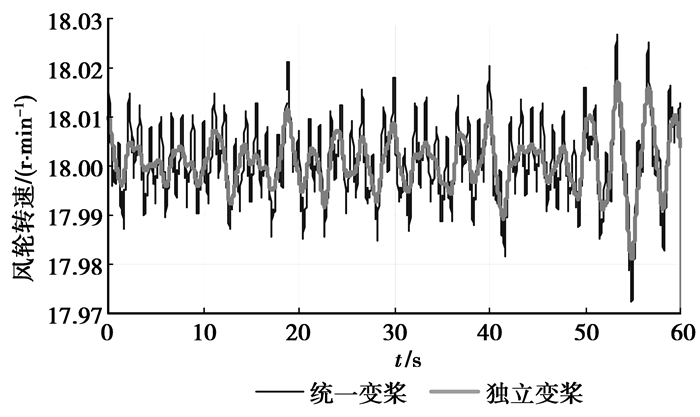
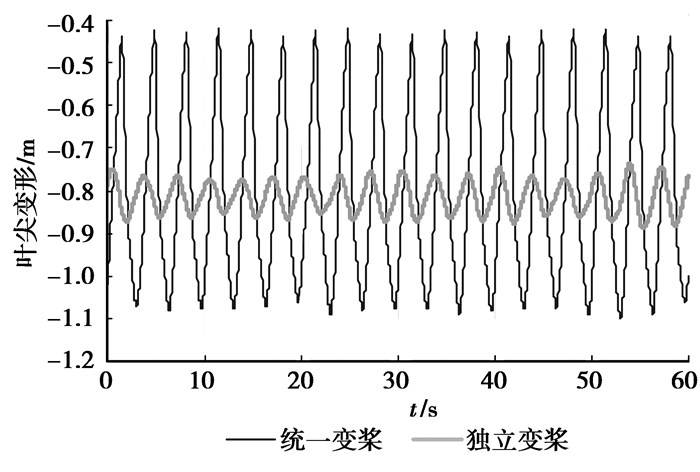
4.1 发电性能分析比较
将2 MW风力发电机分别进行统一变桨和独立变桨情况下的性能分析。分析结果见图 5~图 8。从分析结果来看,可以看出独立变桨下的性能参数的平均值虽然和统一变桨下的平均值差不多,但是参数摆动的幅值比统一变桨情况下要小很多,这表明在独立变桨情况下的总体性能相对统一变桨要稳定。
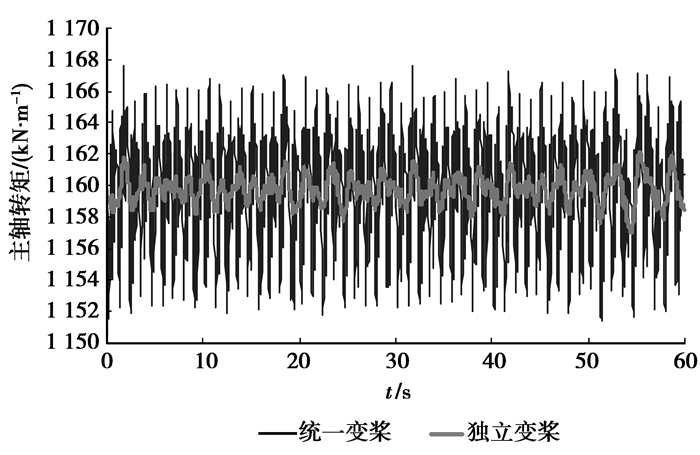
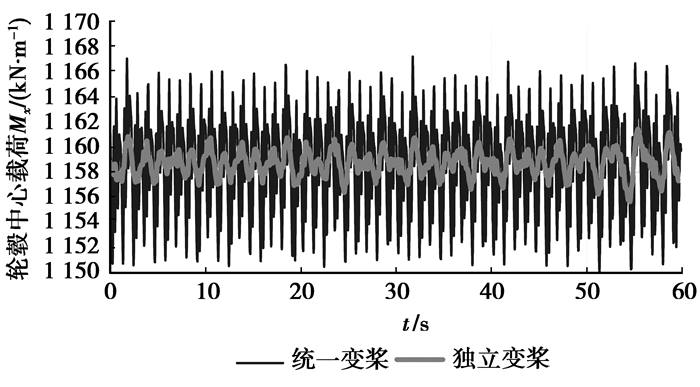
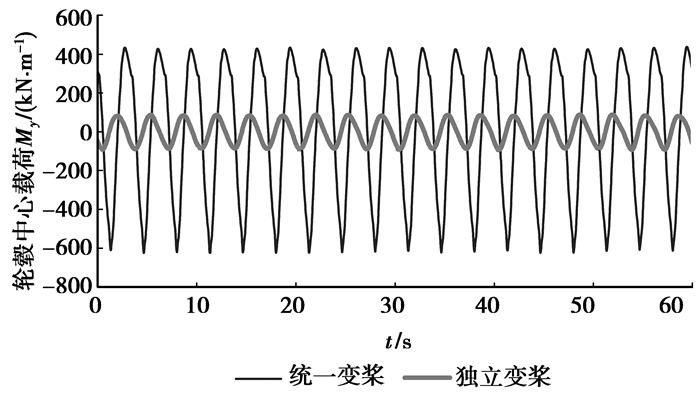
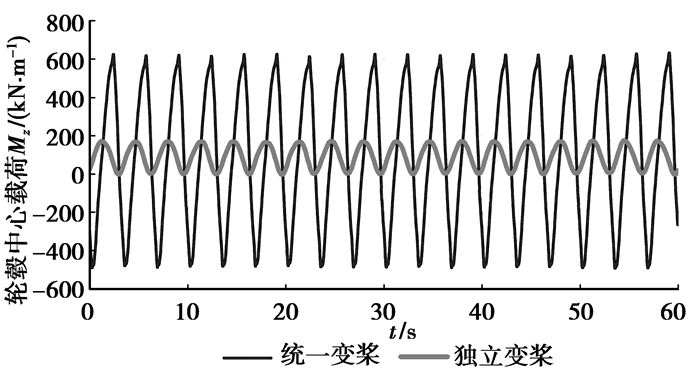
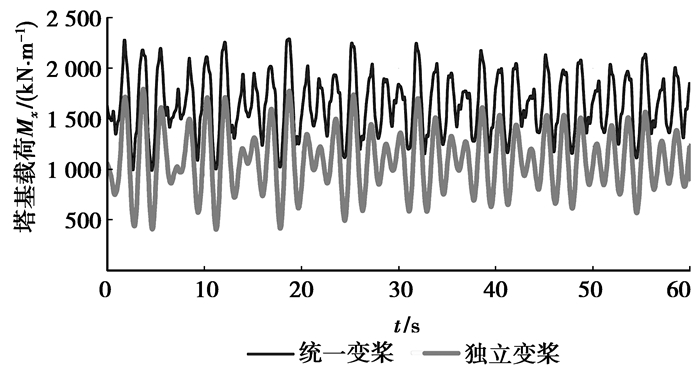
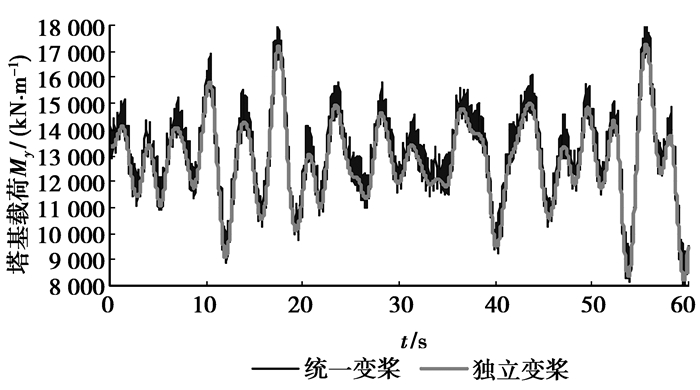
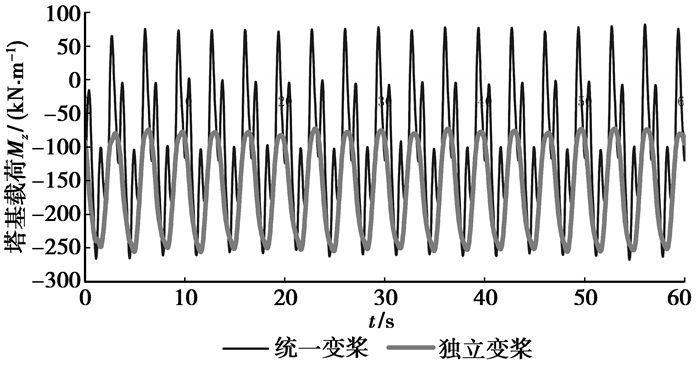
4.2 载荷计算
对风力发电机组的载荷进行计算,由于计算数据太多,仅列出轮毂中心和塔基载荷,比较独立变桨下的受载和统一变桨下的受载情况。计算结果见图 9~图 14。从计算结果来看,可以看出独立变桨下的载荷的平均值虽然和统一变桨下的平均值差不多,但是载荷波动幅值比统一变桨情况下要小很多,这表明在独立变桨情况下的受载相对统一变桨要稳定。通过独立变桨,可以降低风力发电机的载荷,减少维护费用,延长风机的使用寿命。
5 结论
以大型风力发电机组为研究对象,在风力发电机空气动力学模型的基础上,建立系统状态空间方程,对其进行独立变桨控制设计理论研究,采用MATLAB/SIMULINK实现控制器的编程,分析结果与统一变桨比较,证明了所建立控制模型的有效性,并得到以下结论
1) 由于独立变桨引入风速前馈, 控制器对风速的变化进行动态补偿, 抑制了干扰风速产生过大的气动转矩从而使转速更稳定.因此独立变桨与统一便将相比, 总体性能更稳定。
2) 独立变桨考虑了风剪效应, 将风轮的俯仰力矩和偏航力矩作为控制目标独立地控制每个变桨角, 降低了风轮平面上因风剪导致的不平衡载荷, 改善了整个风轮的受载情况.因此, 在独立变桨情况下的受载相对统一变桨要稳定。可以降低风力发电机的载荷,可以减少维护费用,延长风机的使用寿命。
 2014, Vol. 37
2014, Vol. 37

