2. 重庆通信学院 军用特种电源军队重点实验室, 重庆 400035
2. Key Laboratory of Special Power Supply, Chongqing Communication Institute, Chongqing 400035, China
定子双绕组感应发电机(dual stator-winding induction generator,DWIG)是笼型转子结构感应发电机的一种,比同步发电机体积小、机械强度好、制造工艺简单及经济性好,比双馈感应发电机的笼型转子结构更坚固、无电刷和滑环、易于维护,它在独立电源和变速风力发电系统领域具有广泛的应用前景,目前国内外对DWIG的研究还是一个新的领域[1-4]。DWIG在继承传统感应发电机优点的基础之上,克服了感应发电系统中电力电子装置容量体积较大、谐波成分大等缺陷[5-6],通过调节其励磁无功功率可现在变风速情况下恒压输出。
目前,DWIG的研究主要集中在3个方面:一是对DWIG无功功率容量优化的研究[7-9],二是对DWIG控制策略进行探讨[10-13],三是对DWIG电磁设计的分析[14-16]。而现有文献主要针对DWIG发电系统带纯阻性负载的情况进行研究,并未考虑带感性负载情况,也未对负载电流变化情况下电机的运行性能进行研究。综合考虑风力发电系统中DWIG的运行特点,有必要对风力DWIG的运行特性做进一步探讨。
针对以上问题,文中详细分析了风力DWIG的运行机理和功率关系,讨论了容性负载、阻性负载、感性负载情况下控制绕组电流的求解方法,以1台Y180M-4异步电机为原型,基于Visual Basic 6.0平台研发了适用于风力发电的DWIG电磁设计及运行特性计算软件,分别对DWIG在额定转速和变转速2种运行工况下的运行特性进行了计算。研究了额定转速下,空载建压时励磁电流的变化规律,控制绕组电流、转差率、效率随负载电流的变化规律,分析了变转速下无功功率及控制绕组电流随转速的变化情况。
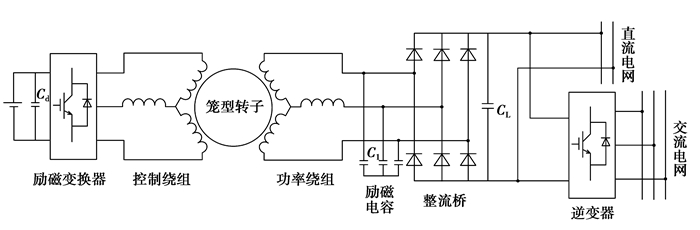
1 运行机理及特点 1.1 风力DWIG系统结构DWIG是一种新型励磁无功功率可调的交流感应发电机。其转子为普通笼型转子结构,但定子上具有2套极对数相同的绕组:一套为功率绕组,输出端接负载;另一套为控制绕组,接有静止的励磁变换器,由变换器提供电机所需的无功功率励磁,采用一定的控制策略,可有效调节功率绕组使之输出恒幅值电压。该发电系统既可直接用于直流输电场合,也可通过逆变器并网运行,其系统结构如图 1所示。
|
图 1 定子双绕组风力感应发电系统结构 |
DWIG输出电压为功率绕组端电压,控制绕组的外电压即为励磁变换器端电压,转子绕组为笼型结构因此无外电压。根据电机学知识,可得功率绕组电压平衡方程式
| $ \left. \begin{array}{l} {{\dot E}_{\rm{p}}} + {{\dot U}_{\rm{p}}} + {{\dot I}_{\rm{p}}}\left( {{R_{\rm{p}}} + j{X_{{\rm{ \mathsf{ σ} p}}}}} \right)\\ {{\dot E}_{\rm{p}}} = - j4.44{f_1}{N_{\rm{p}}}{K_{{\rm{wp}}}}{{\mathit{\dot \Phi }}_{\rm{m}}} \end{array} \right\}, $ | (1) |
式中:Rp和Xσp分别为功率绕组的电阻和漏抗;
DWIG在转速或负载发生变化的情况下,工作频率f1、功率绕组电流Ip均会发生变化,功率绕组端电压Up将随之产生波动。此时,若要维持功率绕组恒定端电压输出,就需要通过控制绕组调节
气隙磁场
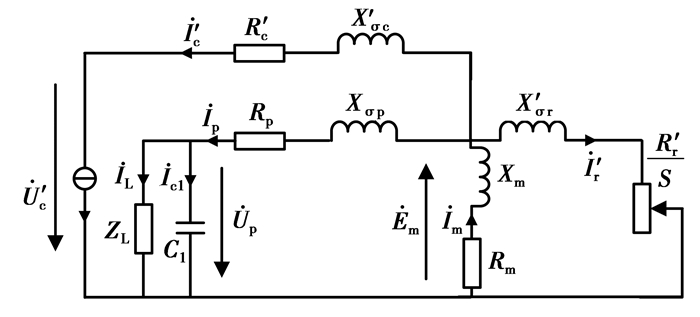
|
图 2 DWIG接整流负载时等效电路图 |
与等效电路对应的基本方程为
| $ \left. \begin{array}{l} {{\dot E}_{\rm{p}}} + {{\dot U}_{\rm{p}}} + {{\dot I}_{\rm{p}}}\left( {{R_{\rm{p}}} + j{X_{{\rm{ \mathsf{ σ} p}}}}} \right)\\ {{\dot E'}_{\rm{c}}} = {{\dot U'}_{\rm{c}}} + {{\dot I'}_{\rm{c}}}\left( {{{R'}_{\rm{c}}} + j{{X'}_{{\rm{ \mathsf{ σ} c}}}}} \right)\\ {{\dot E'}_{\rm{r}}} = {{\dot I}_{{\rm{rs}}}}\left( {\frac{{{{R'}_{\rm{r}}}}}{s} + j{{X'}_{{\rm{ \mathsf{ σ} r}}}}} \right)\\ {{\dot E}_{\rm{p}}} = {{\dot E'}_{\rm{c}}} = {{\dot E'}_{\rm{r}}} = {{\dot E}_{\rm{m}}} = - {{\dot I}_{\rm{m}}}{Z_{\rm{m}}}\\ {{\dot I}_{\rm{p}}} + {{\dot I'}_{\rm{c}}} + {{\dot I'}_{\rm{r}}} = {{\dot I}_{\rm{m}}} \end{array} \right\}, $ | (2) |
式中:R′c、R′r分别为归算后的控制绕组和转子绕组电阻;X′σc和X′σr分别为归算之后的控制绕组和转子绕组漏抗;s为转差率。
1.3 DWIG功率平衡关系DWIG之所以能恒压输出,得益于控制绕组对励磁无功功率的调节,因此在关注有功功率输出的同时,也有必要对无功功率的流向进行较为详细的分析。现参照图 2的等效电路,对DWIG功率平衡关系进行探讨。
1.3.1 有功功率DWIG在发电状态时,忽略励磁器件损耗和电阻损耗,即控制绕组提供纯无功功率[7],因此其端口有功功率为零。原动机拖动电机转子加速超过气隙磁场转速,使转差率为负值,此时总机械功率Pmec及电磁功率Pe[17]为
| $ {P_{{\rm{mec}}}} = {P_1} - {p_{{\rm{fw}}}} - {p_\Delta }, $ | (3) |
| $ {P_{\rm{e}}} = {P_{{\rm{mec}}}} - {p_{{\rm{cur}}}}, $ | (4) |
式中:P1为原动机输入机械功率;pfw为通风及机械摩擦损耗;pΔ为附加损耗;pcur为转子铜耗。
其输出功率P2为
| $ {P_2} = {P_{\rm{e}}} - {p_{{\rm{cup}}}} - {p_{{\rm{cuc}}}} - {p_{{\rm{fe}}}}, $ | (5) |
式中:pcup为功率绕组铜耗;pcuc为控制绕组铜耗;pfe为定子铁耗。
在上述分析基础上可得其功率流向,如图 3所示。
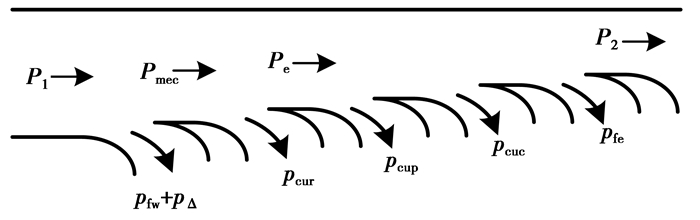
|
图 3 DWIG有功功率流图 |
设控制绕组输入无功功率为Qc;控制绕组漏抗无功功率为Qcσ;转子漏抗无功功率为Qcr;功率绕组漏抗无功功率为Qpσ;激磁电抗无功功率为Qm;励磁电容无功功率为为Qc1;负载无功功率为QL。以下分控制绕组补偿和吸收无功功率2种情况进行分析。
当励磁电容提供的无功功率Qc1少于恒压输出所需无功功率时,控制绕组无功功率Qc补偿所需无功功率,Qc呈容性。此时各无功功率的关系为
| $ {Q_{\rm{c}}} + {Q_{{\rm{c1}}}} = {Q_{\rm{m}}} + {Q_\sigma } + {Q_{\rm{L}}}, $ | (6) |
式中,漏抗无功功率Qσ=Qcσ+Qrσ+Qpσ。
在上述前提下各无功功率关系如图 4(a)所示。
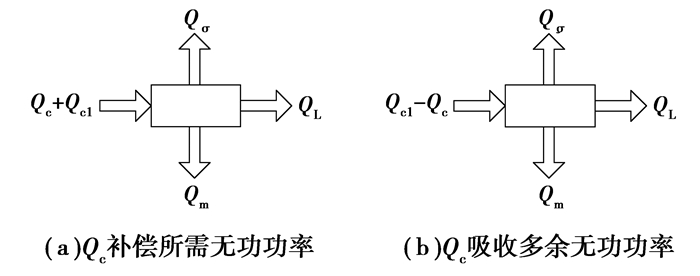
|
图 4 DWIG无功功率流图 |
当励磁电容提供的无功功率超过恒压输出所需无功功率时,控制绕组无功功率Qc吸收多余无功功率,Qc呈感性。此时各无功功率的关系为
| $ {Q_{{\rm{c1}}}} - {Q_{\rm{c}}} = {Q_{\rm{m}}} + {Q_\sigma } + {Q_{\rm{L}}}, $ | (7) |
这时无功功率的流向,如图 4(b)所示。
1.4 风力DWIG特点1) 传统异步发电系统中,无功功率调节装置均与负载有直接电路的联系,在控制过程中会引入较大的谐波成分。而DWIG励磁变换器与负载没有直接的电气连接,只有磁的耦合,提高了系统的电磁兼容性能。
2) 相对于同步发电机而言,DWIG具有功率密度高、结构简单、机械强度高的特点[18]。
3) 该系统可实现较宽风速范围内恒压直流输出,既适用于风力发电领域,亦可逆变后并网运行。
4) 电机输出功率特性随风力机的输出功率特性变化而变化。
5) 与同步发电机不同,DWIG功率绕组电流大小是未知的,因为它与通过励磁电容的电流有关。文中通过式(8)来确定电枢电流及功率因数,为
| $ \left. \begin{array}{l} {I_{{\rm{pl}}}} = {I_{\rm{p}}}\cos \varphi = {I_{\rm{L}}}\cos {\varphi _{\rm{L}}}\\ {I_{{\rm{pc}}}} = {I_{\rm{p}}}\sin \varphi = {I_{\rm{L}}}\sin {\varphi _{\rm{L}}} + \omega {C_1}{U_{\rm{p}}} \end{array} \right\}, $ | (8) |
式中:Ipl、Ipc分别为功率绕组电流的有功和无功功率分量;
在风力DWIG系统中,励磁变换器对系统成本和体积有重要影响,而励磁变换器的容量取决于控制绕组电流的大小[8]。因此控制绕组电流大小成为励磁变换器选择的重要依据。同时,由1.3.2节无功功率平衡关系可知,控制绕组无功功率对DWIG系统恒压输出性能有直接的影响。综上所述,就需要对控制绕组电流计算进行分析。接下来通过等效电路和相量图相结合的方法对控制绕组电流的计算进行推导。
为计算方便,现做以下假设:
1) 忽略电机内部磁滞损耗和涡流损耗,即Rm=0;
2) 假定采用理想控制策略,使控制绕组提供纯无功功率电流,忽略掉少许器件损耗和控制绕组电阻R′c的损耗[6],即用于磁场调节的
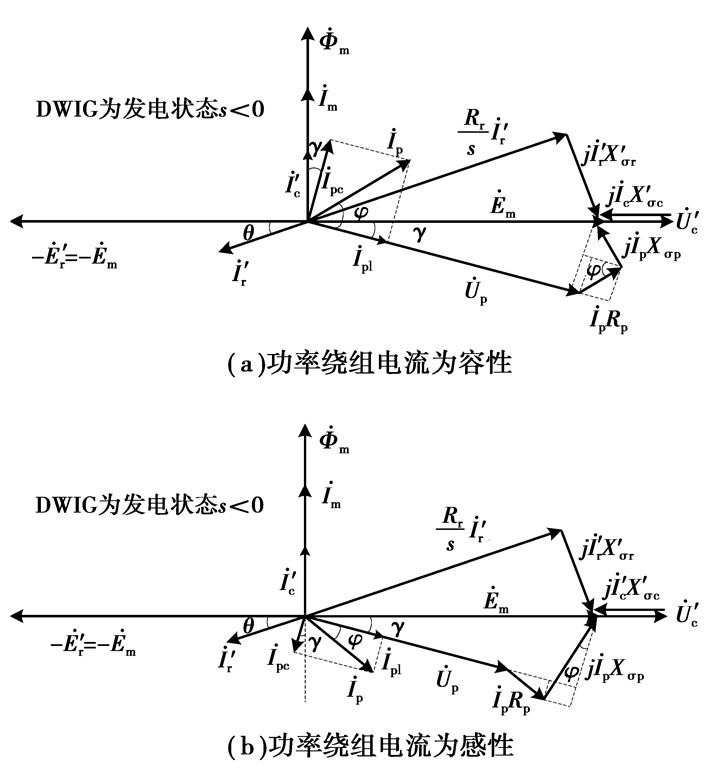
根据图 2的等效电路并结合式(8)可知,当负载为容性、阻性或者感性较弱的情况下,功率绕组电流呈容性,表现为功率绕组电流超前于电压,其相量图如图 5(a)所示;当负载表现出较强感性时,功率绕组电流呈感性,表现为功率绕组电流滞后于电压,其相量图如图 5(b)所示。
|
图 5 DWIG相量图 |
文中先对图 5(a),即功率绕组电流为容性的情况进行分析,图中γ为
| $ {{\dot I}_{\rm{p}}} = {{\dot I}_{{\rm{pc}}}} + {{\dot I}_{{\rm{pl}}}}, $ | (9) |
| $ \left. \begin{array}{l} {{I'}_{\rm{r}}} = \frac{{{E_{\rm{m}}}}}{{\sqrt {{{\left( {\frac{{{{R'}_{\rm{r}}}}}{s}} \right)}^2} + X_{{\rm{ \mathsf{ σ} r}}}^{'2}} }}\\ {I_{\rm{m}}} = \frac{{{E_{\rm{m}}}}}{{{X_{\rm{m}}}}} \end{array} \right\}, $ | (10) |
| $ \left. \begin{array}{l} \cos \gamma = \frac{{{U_{\rm{p}}} - \left( {{I_{{\rm{pc}}}}{X_{{\rm{ \mathsf{ σ} p}}}} - {I_{{\rm{pl}}}}{R_{\rm{p}}}} \right)}}{{{E_m}}}\\ \sin \gamma = \frac{{{I_{{\rm{pl}}}}{X_{{\rm{ \mathsf{ σ} p}}}} + {I_{{\rm{pc}}}}{R_{\rm{p}}}}}{{{E_m}}}\\ \sin \theta = \frac{{{{I'}_{\rm{r}}}{{X'}_{{\rm{ \mathsf{ σ} r}}}}}}{{{E_m}}} \end{array} \right\}, $ | (11) |
| $ {E_{\rm{m}}} = \sqrt {{{\left( {{U_{\rm{p}}} - {I_{{\rm{pc}}}}{X_{{\rm{ \mathsf{ σ} p}}}} + {I_{{\rm{pl}}}}{R_{\rm{p}}}} \right)}^2} + {{\left( {{I_{{\rm{pl}}}}{X_{{\rm{ \mathsf{ σ} p}}}} + {I_{{\rm{pc}}}}{R_{\rm{p}}}} \right)}^2}} , $ | (12) |
| $ {{I'}_{\rm{c}}} = {I_{\rm{m}}} - {I_{{\rm{pc}}}}\cos \gamma + {I_{{\rm{pl}}}}\sin \gamma + {{I'}_{\rm{r}}}\sin \theta 。$ | (13) |
将式(9)、(10)、(11)带入式(13),化简可得
| $ \begin{array}{*{20}{c}} {{{I'}_{\rm{c}}} = \frac{{{E_{\rm{m}}}}}{{{X_{\rm{m}}}}} + \frac{{I_{\rm{p}}^2{X_{{\rm{ \mathsf{ σ} p}}}} - {U_{\rm{p}}}{I_{\rm{p}}}\sin \varphi }}{{{E_{\rm{m}}}}} + }\\ {\frac{{{E_{\rm{m}}}{{X'}_{{\rm{ \mathsf{ σ} r}}}}}}{{{{\left( {\frac{{{{R'}_{\rm{r}}}}}{s}} \right)}^2} + X_{{\rm{ \mathsf{ σ} r}}}^{'2}}}。} \end{array} $ | (14) |
对于图 5(b),即在功率绕组电流为感性情况下,按照同样的方法推导可得
| $ \begin{array}{*{20}{c}} {{{I'}_{\rm{c}}} = \frac{{{E_{\rm{m}}}}}{{{X_{\rm{m}}}}} + \frac{{I_{\rm{p}}^2{X_{{\rm{ \mathsf{ σ} p}}}} + {U_{\rm{p}}}{I_{\rm{p}}}\sin \varphi }}{{{E_{\rm{m}}}}} + }\\ {\frac{{{E_{\rm{m}}}{{X'}_{{\rm{ \mathsf{ σ} r}}}}}}{{{{\left( {\frac{{{{R'}_{\rm{r}}}}}{s}} \right)}^2} + X_{{\rm{ \mathsf{ σ} r}}}^{'2}}}。} \end{array} $ | (15) |
DWIG为励磁无功功率可调的新型感应发电机,其运行特性有别于常规感应发电机和同步发电机。为了对其性能有进一步的了解,文中先对DWIG在额定转速下的性能进行研究,采用Visual Basic 6.0平台研发的DWIG电磁设计及运行特性计算软件。DWIG样机以Y180M4异步电机为原型,其主要设计参数如表 1所示。
| 表 1 DWIG样机主要设计参数 |
运行特性的计算公式由等效电路和相量图相结合推导而来。为使计算更接近实际情况,研究过程中充分考虑了磁路饱和及负载电流变化对电机参数的影响,即运行特性公式中的每个点所对应的电机参数都经过电磁设计程序计算得到。
3.1 空载特性定义DWIG空载特性为:空载电压与励磁电流Im的关系曲线,即Upo=f(Im)。
空载时,有IL=0、Up=Upo由式(8)、式(12)可得
| $ {E_{\rm{m}}} = \sqrt {{{\left( {{U_{{\rm{po}}}} - \omega {C_1}{U_{{\rm{po}}}}{X_{{\rm{ \mathsf{ σ} p}}}}} \right)}^2} + {{\left( {\omega {C_1}{U_{{\rm{po}}}}{R_{\rm{p}}}} \right)}^2}} , $ | (16) |
| $ {I_{\rm{p}}} = {I_{{\rm{cl}}}} = \omega {C_1}{U_{{\rm{po}}}}。$ | (17) |
由于此时功率绕组端只接励磁电容,因此功率绕组电流呈容性,因此将式(16)、式(17)代入式(14),并考虑到空载时s≈0,化简得
| $ \begin{array}{*{20}{c}} {{{I'}_{\rm{c}}} = {U_{{\rm{po}}}}\left[ {\frac{{\sqrt {{{\left( {1 - \omega {C_1}{X_{{\rm{ \mathsf{ σ} p}}}}} \right)}^2} + {{\left( {\omega {C_1}{R_{\rm{p}}}} \right)}^2}} }}{{{X_{\rm{m}}}}} - } \right.}\\ {\frac{{\omega {C_1}}}{{\sqrt {{{\left( {1 - \omega {C_1}{X_{{\rm{ \mathsf{ σ} p}}}}} \right)}^2} + {{\left( {\omega {C_1}{R_{\rm{p}}}} \right)}^2}} }} + }\\ {\left. {\frac{{{{\left( {\omega {C_1}} \right)}^2}{X_{{\rm{ \mathsf{ σ} p}}}}}}{{\sqrt {{{\left( {1 - \omega {C_1}{X_{{\rm{ \mathsf{ σ} p}}}}} \right)}^2} + {{\left( {\omega {C_1}{R_{\rm{p}}}} \right)}^2}} }}} \right]。} \end{array} $ | (18) |
由式(18)可知,电机的饱和程度会使控制绕组电流呈非线性变化,同时也体现了励磁电容和控制绕组共同励磁建压的特点。
总励磁电流Im由电磁设计程序计算得到,励磁电容电流Ic1由式(17)得出。
现按励磁电容不同容值分别讨论其建压情况,计算结果如图 6所示。

|
图 6 空载特性曲线 |
当励磁电容为100 μF时,由图 6(a)可知,电容的伏安特性曲线Upo=f(Ic1)和空载特性曲线Upo=f(Im)没有交点,仅靠励磁电容无法完成自励建压[15],即励磁电容较小,不能满足电机建压所需无功功率。要维持端电压的上升,就需要控制绕组补偿所需的励磁无功功率。图中曲线表明,随着控制绕组电流的增加,端电压可保持逐渐上升的趋势。
当励磁电容为150 μF时,如图 6(b)所示,电容的伏安特性曲线Upo=f(Ic1)和空载特性曲线Upo=f(Im)相交于点A,因此励磁电容可建立稳定的空载电压于A点。实际上,在A点之前对于某个电压而言,励磁电容所提供的励磁电流大于该电压所需励磁电流,因此电压会上升直到A点保持稳定。在A点之前,若要将电压维持在某一点,控制绕组就必须吸收多余的励磁无功功率,此时控制绕组电流出现负值的情况。同理,由图可知,在A点以后,励磁电容所提供无功功率已不能维持端电压的继续升高,此时若要输出高于A点的端电压,就需要控制绕组补偿励磁无功功率。图中曲线表明,在A点以后,端电压会随着控制绕组电流的增加而上升。
上述分析表明了励磁电容和控制绕组共同励磁的事实,控制绕组可对励磁无功功率进行调节实现空载建压。
3.2 调节特性定义DWIG调节特性为:在额定电压、额定负载功率因数下,DWIG控制绕组电流与负载电流的关系曲线,即Ic=f(IL)。
DWIG具有在变负载情况下维持恒定端电压的能力,因此有必要对控制绕组电流随负载电流变化情况进行研究。由式(8)、式(12)可得
| $ {E_{\rm{m}}} = \sqrt {{G^2} + {H^2}} , $ | (19) |
式中:
这里要注意的是,负载电流变化时,需要通过式(8)来推导功率绕组电流超前或滞后电压的情况,控制绕组电流要按照第2节中容性和感性2种情况分别计算。
实际上,对文中研究的DWIG样机而言,负载电流较小时,由于负载功率因数
由式(14)、(15)、(19)可得控制绕组电流为
| $ \begin{array}{*{20}{c}} {{{I'}_{\rm{c}}} = \frac{{\sqrt {{G^2} + {H^2}} }}{{{X_{\rm{m}}}}} + \frac{{{{X'}_{{\rm{ \mathsf{ σ} r}}}}\sqrt {{G^2} + {H^2}} }}{{{{\left( {\frac{{{{R'}_{\rm{r}}}}}{s}} \right)}^2} + X_{{\rm{ \mathsf{ σ} r}}}^{'2}}} + }\\ {\frac{{I_{\rm{p}}^2{X_{{\rm{ \mathsf{ σ} p}}}} \mp {U_{\rm{p}}}{I_{\rm{p}}}\sin \varphi }}{{\sqrt {{G^2} + {H^2}} }},} \end{array} $ | (20) |
式中,
当功率绕组电流呈容性时,式(20)右边第3项“
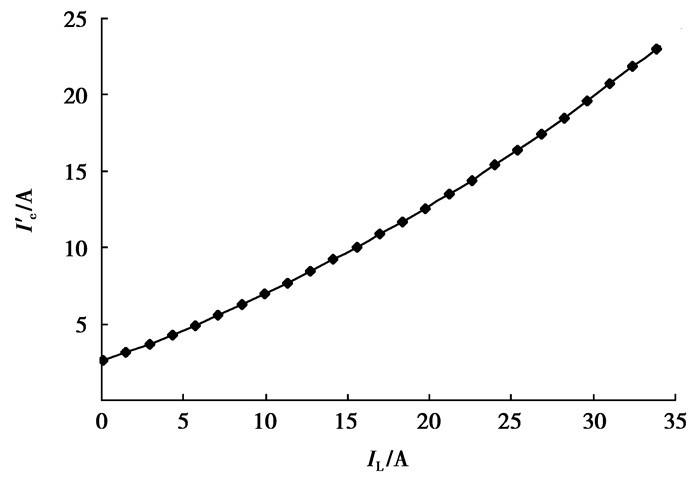
在负载功率因数和端电压保持不变情况下,调节特性计算结果如图 7所示。
|
图 7 调节特性曲线 |
随着负载电流的增大,由式(1)可知,电机漏阻抗压降随Ip增大而增大,要维持端电压恒定就要增加控制绕组提供的励磁无功功率,即表现为控制绕组电流增加,从图 7可知曲线的变化趋势与理论分析的一致性,同时,这也反应了负载电流变化时控制绕组对磁场的调节作用。
3.3 速率特性定义DWIG速率特性为:在额定电压、额定负载功率因数下,DWIG转差率与负载电流的关系曲线,即s=f(IL)。
与感应电动机不同,处于发电状态的DWIG转差率为负值,以下为其计算值推导过程。
由1.3节能量传递关系并结合图 2的等效电路可知,风机传递到定子侧的电磁功率为
| $ {P_{\rm{e}}} = - \frac{{3I_{\rm{r}}^{'2}{{R'}_{\rm{r}}}}}{s}。$ | (21) |
将式(10)中I′r表达式代入式(21),可得
| $ s = \frac{{ - 3E_{\rm{m}}^2{{R'}_{\rm{r}}} + \sqrt {9E_{\rm{m}}^4R_{\rm{r}}^{'2} - 4P_{\rm{e}}^2R_{\rm{r}}^{'2}X_{{\rm{ \mathsf{ σ} r}}}^{'2}} }}{{2{P_{\rm{e}}}X_{{\rm{ \mathsf{ σ} r}}}^{'2}}}。$ | (22) |
忽略电机损耗,有Pe≈P2。将式(19)代入式(22),可得转差率和负载电流之间的关系
| $ s = \frac{{ - 3\left( {{G^2} + {H^2}} \right){{R'}_{\rm{r}}} + \sqrt {9{{\left( {{G^2} + {H^2}} \right)}^2}R_{\rm{r}}^{'2} - 4\left( {{U_{\rm{P}}}{I_{\rm{L}}}\cos \varphi _{\rm{L}}^2} \right)R_{\rm{r}}^{'2}X_{{\rm{ \mathsf{ σ} r}}}^{'2}} }}{{2{U_{\rm{P}}}{I_{\rm{L}}}\cos {\varphi _{\rm{L}}}X_{{\rm{ \mathsf{ σ} r}}}^{'2}}}。$ | (23) |
速率特性计算结果如图 8所示。

|
图 8 速率特性曲线 |
与感应电动机类似,但DWIG处于发电状态,因此其转差率为负值。当负载电流增加时,输出功率增加,由功率平衡关系可知,输入功率要增加,表现为转差率的绝对值是增加的。同时图 8曲线变化规律与文献[19]实验数据中转差率变化规律是一致的,从而佐证了该特性曲线的正确性。
3.4 效率特性定义DWIG效率特性曲线为:在额定电压、额定负载功率因数下,DWIG效率与负载电流的关系曲线,即η=f(IL)。
1.3.1节对电机有功功率平衡关系进行了较为详细的分析,由此易知
| $ \eta = \frac{{{P_2}}}{{{P_1}}} = \frac{{{P_2}}}{{{P_2} + \sum p }} = \frac{{\sqrt 3 {U_{\rm{p}}}{I_{\rm{p}}}\cos \varphi }}{{\sqrt 3 {U_{\rm{p}}}{I_{\rm{p}}}\cos \varphi + \sum p }}, $ | (24) |
式中,
铜耗计算为
| $ \left. \begin{array}{l} {p_{{\rm{cup}}}} = 3I_{\rm{p}}^2{R_{\rm{p}}}\\ {p_{{\rm{cuc}}}} = 3I_{\rm{c}}^{'2}{{R'}_{\rm{c}}}\\ {p_{{\rm{cur}}}} = 3I_{\rm{c}}^{'2}{{R'}_{\rm{c}}} \end{array} \right\}。$ | (25) |
铁耗pfe由电磁设计程序根据磁感应强度查硅钢片损耗曲线计算得到;通风及机械摩擦损耗pfw按照常规感应电机公式计算。由于是铜条转子,因此附加损耗pΔ取0.005倍额定输出功率。
由式(8)可知,在负载功率因数

|
图 9 效率特性曲线 |
由图 9可见,随着功率绕组输出电流IL的增加,效率逐渐上升,当可变损耗等于不变损耗时效率达到最高,此后,损耗增加大于输出功率的增加,效率又呈下降趋势。
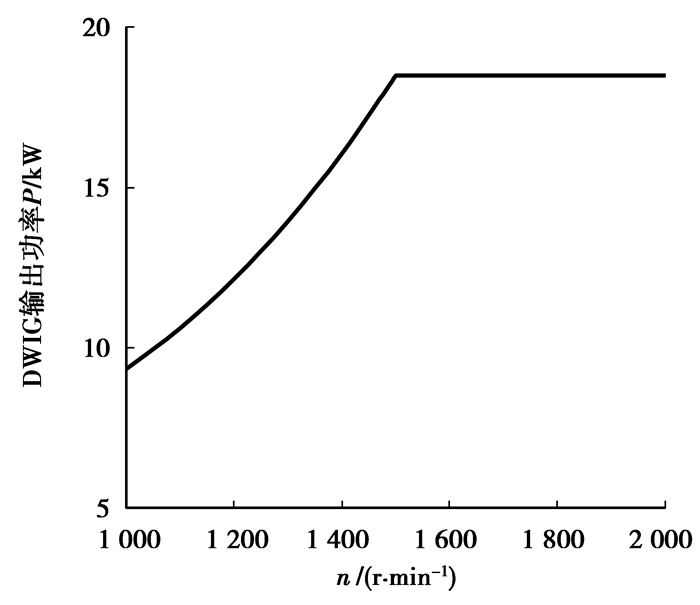
4 变转速运行特性假定采用变桨控制技术的DWIG输出功率曲线如图 10所示。在转速变化过程中,设负载功率因数和负载电压均保持不变,取励磁电容C1=100 μF,在额定转速1 500 r/min之前,负载电流随输出功率增大而增大,额定转速及以上时,负载电流保持恒定不变。
|
图 10 变桨距控制的DWIG输出功率曲线 |
在上述有功功率输出前提下,DWIG在变转速运行过程中要实现恒压,本质在于控制绕组对无功功率的调节作用,表现为控制绕组电流大小的变化,因此有必要对运行过程中无功功率的变化情况进行分析。文中主要研究DWIG变转速下各无功功率随转速变化规律、控制绕组电流随转速变化规律。
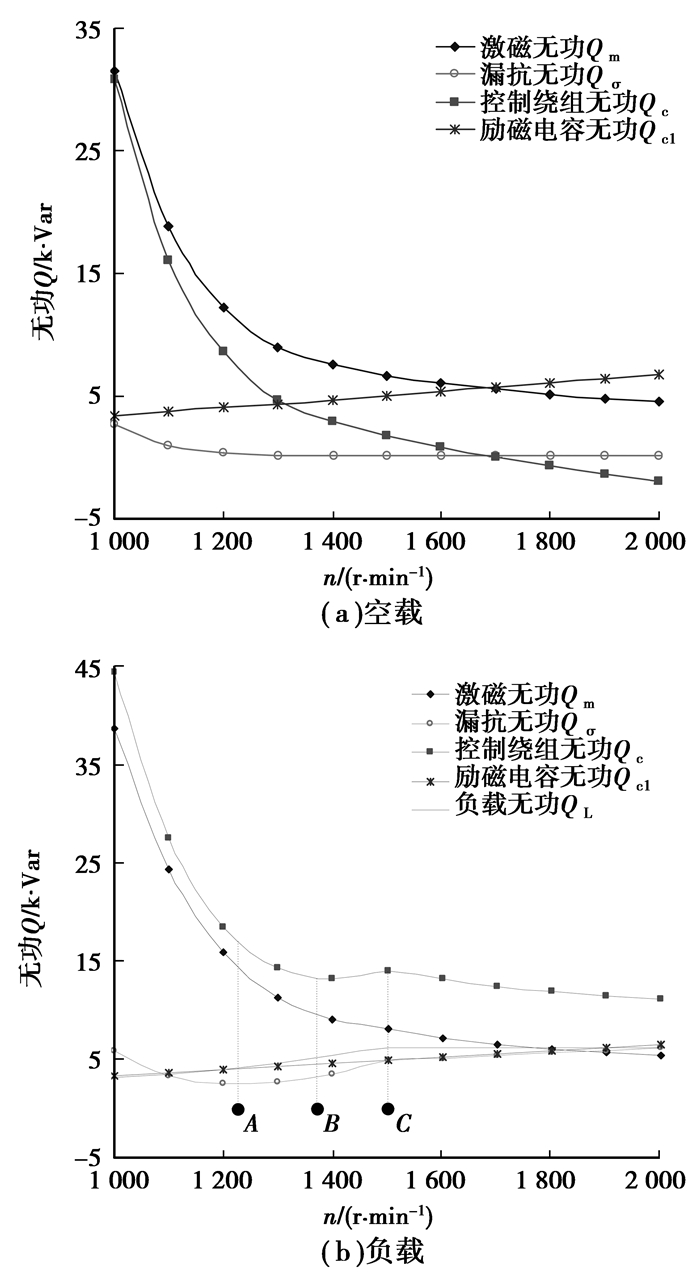
4.1 无功功率与转速关系由DWIG的运行机理可知,要实现恒压输出,励磁无功功率的调节是关键,因此有必要对其运行过程中各无功功率与转速的变化情况进行分析。根据图 2的等效电路,并结合第1.3.2节中无功功率的分析,可得到DWIG在空载和负载情况下,无功功率随转速变化的关系曲线,分别如图 11(a)、(b)所示。
|
图 11 无功功率随转速变化曲线 |
空载时,DWIG功率绕组输出端仅有励磁电容,此时负载无功功率QL为0。无功功率变化如图 11(a)所示。电机转速较低时,由式(1)可知,频率f1较低,要维持端电压的恒定,所需励磁无功功率Qm较多,而f1较低时,由式(17)可知,励磁电容电流Ic1较小,励磁电容所提供的无功功率Qc1不满足恒压励磁需求。因此需要控制绕组提供无功功率补偿,同时功率绕组和转子绕组电流较小,漏抗无功功率Qσ以控制绕组无功功率Qcσ为主;随着转速的增加,恒压输出所需励磁无功功率Qm逐渐减少,工作频率f1的增加会使得流过励磁电容的电流Ic1增加,这使得励磁电容所提供无功功率Qc1随工作频率的增加而增加,因此控制绕组所需补偿无功功率Qc随之减少,漏抗无功功率Qσ也随之减少。
当励磁电容提供无功功率Qc1超过维持恒定端电压所需无功功率Qm时,控制绕组无功功率Qc呈感性,吸收多余容性无功功率,从而维持端电压的恒定,图中表现为负值。
图 11(a)表明,当控制绕组补偿励磁无功功率时,每个转速下控制绕组和励磁电容无功功率之和与励磁无功功率与漏抗无功功率之和是相等的,这与式(6)的无功功率平衡理论分析一致;当控制绕组吸收多余励磁无功功率时,每个转速下励磁电容与控制绕组无功功率之差和励磁无功功率与漏抗无功功率之和相等,这与式(7)的无功功率平衡理论分析一致。
负载时,变转速过程中DWIG输出功率满足图 10所给出的特性曲线,这时无功功率随转速变化如图 11(b)所示。负载时所需励磁无功功率Qm较多,但其无功功率变化情况与空载时类似。由于带感性负载,控制绕组补偿无功功率Qc也相对空载时多,漏抗无功功率Qσ相对于空载时有所增加。
A点之前,随着转速的增加,恒压输出所需励磁无功功率Qm减少,励磁电容所提供无功功率Qc1增加,而负载电流的增加会使得负载无功功率QL也相应增加,由于负载功率因数为0.95(感性),因此负载视在功率中无功功率成分较小,QL变化较为平缓,该过程以励磁无功功率Qm的减小为主,总体来讲控制绕组提供无功功率Qc减小。由于控制绕组电流Ic较大,漏抗无功功率Qσ以控制绕组为主,漏抗无功功率Qσ总体表现为减少。
A点之后B点之前,随着转速增加,负载电流增加使得功率绕组和转子绕组电流增加,漏抗无功功率Qσ以功率绕组和转子绕组为主,因此漏抗无功功率Qσ总体表现为增加,而励磁无功功率Qm的减小仍然在该过程中占主导地位,因此控制绕组提供无功功率Qc继续减小。
B点之后C点之前,随着转速增加,励磁无功功率Qm的减小趋于平缓,负载无功功率QL进一步增加,使得控制绕组补偿无功功率Qc出现增加的趋势。
C点之后,超过额定转速1 500 r/min,由DWIG输出功率特性曲线知,此时负载电流保持恒定,负载无功功率QL也保持恒定,随着工作频率的增加,励磁无功功率Qm继续减小,各绕组漏抗值增加,因此总漏抗无功功率Qσ表现为增加,同时励磁电容无功功率Qc1增加,总体表现为控制绕组无功功率Qc减小。
图 11(b)表明,在每个转速下控制绕组和励磁电容励磁无功功率之和与励磁无功功率、负载无功功率及漏抗无功功率之和是相等的,这与式(6)的无功功率平衡理论分析一致。
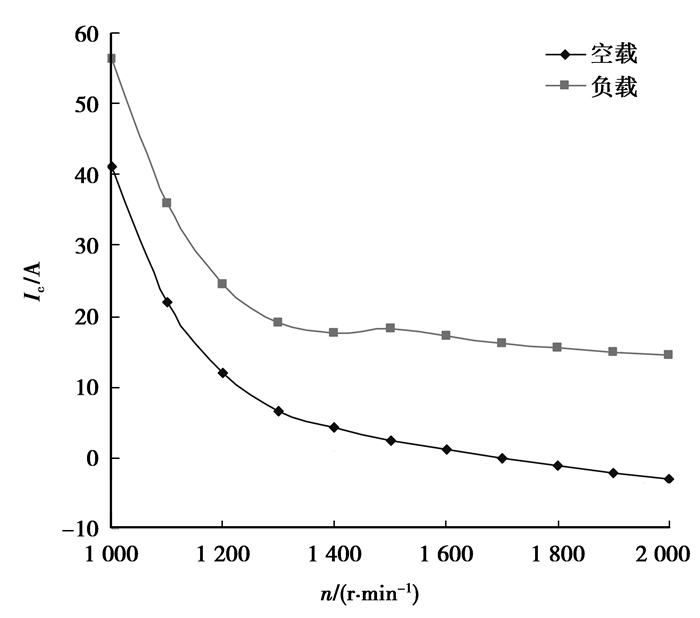
4.2 控制绕组电流与转速关系在上述无功功率分析的基础之上,得到在空载和负载2种情况下,控制绕组电流随转速的变化关系曲线如图 12所示。
|
图 12 控制绕组电流随转速变化曲线 |
可以看出,空载时控制绕组电流随转速的增加而减小,负载时控制绕组电流随转速呈现先减小再略微增加,最后再减少的趋势。这与第4.1节的理论分析一致,从而从机理上证明了控制绕组电流变化的正确性。
5 结论风力DWIG为新型励磁无功功率可调的感应发电机,为对其运行特性有较为深入的研究,文中从原理上对DWIG进行了较为详细的分析之后,运用等效电路和相量图相结合的方法,分析了不同负载情况下控制绕组电流的计算方法,并通过电磁设计程序对额定转速和变转速2种工况下的运行特性进行了研究,理论分析表明了计算结果的正确性和合理性,并得到如下结论:
1) 额定转速时,控制绕组可补偿或吸收空载建压所需无功功率,完成所期望端电压的建压任务;在功率因数和负载端电压保持不变的情况下,控制绕组电流、转差率随负载电流的增大而增大,效率随负载电流的增加先增大后减小。
2) 变速空载运行时,控制绕组无功功率随转速的增大而减小;变转速负载运行时,控制绕组无功功率随转速先减小后增加再减小;控制绕组电流变化规律与之相同。
以上研究揭示了DWIG的运行机理,为样机的工程设计提供了参考依据,同时为其无功功率容量优化的研究奠定了基础。
| [1] | Ojo O, Davidson I E. PWM-VSI inverter-assisted stand-alone dual stator winding induction generator[J]. IEEE Transactions on Industry Applications, 2000, 36(6): 1604–1611. DOI:10.1109/28.887212 |
| [2] | Bu F F, Huang W X, Hu Y W, et al. An integrated AC and DC hybrid generation system using dual-stator-winding induction generator with static excitation controller[J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 810–812. |
| [3] | Liu L S, Qu D c, Lu C H. Research on performances of dual stator-winding induction generator system with low voltage and large current[C]//Proceedings of 2010 International Conference on Intelligent System Design and Engineering Application, October 13-14, 2010, Changsha, China. Piscataway:IEEE Press, 2010, 2:236-239. |
| [4] |
施凯, 黄文新, 胡育文, 等.
定子双绕组感应电机风力发电系统的低电压穿越特性分析[J]. 电力系统自动化, 2012, 36(17): 28–32.
SHI Kai, HUANG Wenxin, HU Yuwen, et al. Characteristics analysis on low voltage ride through of dual stator-winding induction generator wind power system[J]. Automation of Electric Power Systems, 2012, 36(17): 28–32. (in Chinese) |
| [5] |
胡育文, 黄文新, 张兰红.
异步电机起动/发电系统的研究[J]. 电工技术学报, 2006, 21(5): 7–13.
HU Yuwen, HUANG Wenxin, ZHANG Lanhong. Research on employing starter/generator system[J]. Transactions of China Electrotechnical Society, 2006, 21(5): 7–13. (in Chinese) |
| [6] | Liu L S, Zhang K, Hu Y W. Research on dual stator-winding induction generator with wind energy[C]//Proceddings of 2009 International conference on Energy and Environment Technology, October 16-18, 2009, Guilin, Guangxi. Piscataway:IEEE Press, 2009, 1:790-793. |
| [7] | Li Y, Hu Y W, Huang W X, et al. The capacity optimization for the static excitation controller of the dual-stator-winding induction generator operating in a wide speed range[J]. IEEE Transaction on Industrial Electronics, 2009, 56(2): 530–541. |
| [8] | Bu F F, Huang W X. An excitation capacitor optimized dual stator-winding induction generator with the static excitation controller for wind power application[J]. IEEE Transactions on Energy Conversion, 2011, 26(1): 122–131. |
| [9] |
施凯, 黄文新, 胡育文, 等.
宽风速运行的定子双绕组感应电机风力发电系统励磁电容的优化方案[J]. 电工技术学报, 2012, 27(7): 86–93.
SHI Kai, HUANG Wenxin, HU Yuwen, et al. Optimal scheme of excitation capacitor for dual stator-winding induction generator wind power system over a wide wind speed[J]. Transactions of china Electrotechnical Society, 2012, 27(7): 86–93. (in Chinese) |
| [10] | Bu F F, Huang W X, Hu Y W, et al. An instantaneous slip frequency control strategy for the dual stator-winding induction generator variable frequency AC power system[C]//Proceedings of the 201227th Annual IEEE Applied Power Electronics Conference and Exposition, February 5-9, 2012, Oriando, FL. Piscataway:IEEE Press, 2012:1673-1675 |
| [11] | Shi K, Huang W X, Hu Y W, et al. An indirect-field-oriented dual stator-winding induction generator for the wind power system applications[C]//Proceedings of 2009 IEEE World Non-Grid-Connected Wind Power and Energy Conference, September 24-26, 2009, Nianjing, China. Piscataway:IEEE Press, 2009:1-5. |
| [12] |
施凯, 黄文新, 胡育文, 等.
定子双绕组感应发电系统的滞环电流控制方法[J]. 电机与控制学报, 2012, 16(4): 19–24.
SHI Kai, HUANG Wenxin, HU Yuwen, et al. Hysteresis current control method for the dual stator-winding induction generator system[J]. Electric Machines and Control, 2012, 16(4): 19–24. (in Chinese) |
| [13] | Bu F F, Huang W X, Hu Y W, et al. A stand-alone dual stator-winding induction generator variable frequency AC power system[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 10–13. |
| [14] | Wang D, Ma W M, Guo Y. Optimal design of a self-excited capacitor in a dual-stator winding induction generator[J]. Electric Power Applications, 2009, 3(4): 334–342. |
| [15] |
刘陵顺, 周洪庆, 胡育文.
低压大电流输出的双绕组感应发电机系统优化设计[J]. 电机与控制应用, 2009, 36(11): 1–11.
LIU Lingshun, ZHOU Hongqing, HU Yuwen. Optimal design of dual stator-winding induction generator system with low voltage and large current output[J]. Electric Machines & Control Application, 2009, 36(11): 1–11. DOI:10.3969/j.issn.1673-6540.2009.11.001 (in Chinese) |
| [16] | Huang W X, Hu Y W, Bu F F, et al. The magneto motive force of a novel dual stator-winding induction generator[C]//Proceedings of 2010 IEEE Energy Conversion Congress and Exposition, September 12-16, 2010, Atlanta, GA. Piscataway:IEEE Press, 2010:3582-3587. |
| [17] | 唐任远, 顾国彪, 秦和, 等. 中国电气工程大典(第9卷):电机工程[M]. 北京: 中国电力出版社, 2008: 462-463. |
| [18] |
张波涛, 马伟明, 王东.
3相定子电压定向的12/3相双绕组异步发电机励磁控制的实现[J]. 电机工程学报, 2004, 24(2): 135–138.
ZHANG Botao, MA Weiming, WANG Dong. Implementation of the excitation control with 3 phase stator voltage oriented in the 12/3 phase double-winding induction generator[J]. Chinese Society of Electrical Engineering, 2004, 24(2): 135–138. (in Chinese) |
| [19] |
吴新振, 王祥珩.
双绕组高速异步发电机控制绕组电流和定子频率的确定[J]. 电机工程学报, 2007, 27(18): 23–29.
WU Xinzhen, WANG Xiangheng. Determination of control winding current and stator frequency for dual stator-winding high-speed induction generator[J]. Chinese Society of Electrical Engineering, 2007, 27(18): 23–29. DOI:10.3321/j.issn:0258-8013.2007.18.005 (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


