2. 哈尔滨工业大学 机器人技术与系统国家重点实验室, 哈尔滨 150080
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China
近年来,中国的煤矿事故频发,给国家和个人都带来了巨大的损失,开发应用于矿难搜索的机器人将会为救援工作带来帮助。矿难搜索机器人必须能够深入到事故发生的现场才能带来最宝贵的井下环境信息,提供给救援人员参考。在通讯不畅、环境信息未知的情况下,通过所携带的传感器对机器人进行定位从而使得机器人能够安全避障,到达指定的目的地,有着实际应用的需要[1]。为此,矿难搜索机器人作为一种移动机器人,其同步定位与地图的构建方法是实现自主导航的一个关键问题[2]。由于灾后井下恶劣条件的限制,机器人的定位导航有别于地面行走机器人的导航,它要求有较高的自主性和抗干扰性能[3]。为此,传统的SLAM方法并不能满足相应的精度要求,需要性能更佳的方法。
目前较为常见的SLAM解决方法有基于卡尔曼滤波(KF)估计的方法[4],基于扩展卡尔曼滤波(EKF)估计的方法[5],基于无迹卡尔曼滤波(UKF)的方法[6]以及基于粒子滤波器的方法[7]等。基于卡尔曼滤波的各种方法往往要求系统的线性程度比较高,并且需要较大的计算量与存储空间。而粒子滤波器是一种基本统计工具,其核心是基于贝叶斯采样估计的顺序重要采样(sequential importance sampling,SIS)方便易行,所需存储空间相对较低,对系统的线性和高斯性要求不高,当粒子数足够多的时候可以逼近任何概率分布,因而成为了目前较为常用的SLAM解决方法。Montemerlo等人便基于此提出了一种基于特征地图的FastSLAM方法[8-9]。然而FastSLAM方法也存在粒子滤波器定位中的一些常见问题。例如,由于是基于先验概率的采样,往往也需要较多的粒子才能提高定位与地图创建精度,而且随着定位过程的深入,也存在粒子多样性退化以及粒子耗尽等问题。为此许多学者都提出了改进的粒子滤波器算法来改善FastSLAM方法。例如,Dong等将遗传算法引入到粒子滤波算法中,从而可以利用采集到的原始传感器数据完成定位[10]。Lee等在重采样后,利用粒子群优化算法更新机器人的位姿,减弱粒子的退化问题[11]。Lee等在重采样后,利用粒子群优化算法更新机器人的位姿,减弱粒子的退化问题[11]。Chatterjee等依据模糊神经系统离线的对SLAM中的参数进行学习[12]。厉茂海等利用进化策略对粒子所表示的系统状态进行优化,使得粒子能准确近似后验概率分布[13]。
人工鱼群算法是一种基于动物自治体的优化方法,是李晓磊等于2002年提出来的,主要可以用于解决函数优化等问题[14]。因此,将人工鱼群算法和粒子滤波器相结合,从而使得算法可以在相同的粒子数条件下得到更高的定位与路标估计精度,并且基于定向重采样的方法,解决了粒子匮乏问题。仿真实验证明了方法的正确性与有效性。
1 SLAM问题描述1986年Smith和Cheeseman等人首先提出了SLAM问题[15],可以将其理解为是先有鸡还是先有蛋的两难问题。因为机器人的定位就是决定机器人在环境中的位置,而为了构建未知环境地图又必须了解机器人的位置。早期的研究都将两个模型独立研究,忽略了两者的关联性,使得研究陷入了暂时的停顿。但是随着理念的突破,许多学者认识到需要将运动模型与观测模型结合起来研究,进而相互促进,相互影响。为此,如果设定机器人在k时刻的位姿状态向量为xk,k时刻能够观测到的路标位置状态向量为mk,k时刻实际路标观测值为zk,k时刻的机器人输入控制向量为uk,这样SLAM问题就转换为对后验概率密度分布p(xk,mk|zk,uk)的估计问题。
基于上述的设定,依据贝叶斯概率公式可以通过先验概率密度分布求取后验概率密度分布如式(1)所示
| $ \begin{array}{l} \;\;\;\;\;\;p\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{m}}_k}\left| {{z_k}, {\mathit{\boldsymbol{u}}_k}} \right.} \right) = \\ \frac{{p\left( {{z_k}\left| {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{m}}_k}, {z_{k - 1}}} \right., {\mathit{\boldsymbol{u}}_k}} \right)p\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{m}}_k}\left| {{z_{k - 1}}, {\mathit{\boldsymbol{u}}_k}} \right.} \right)}}{{p\left( {{z_k}\left| {{z_{k - 1}}} \right., {\mathit{\boldsymbol{u}}_k}} \right)}}, \end{array} $ | (1) |
其中p(xk,mk|zk-1,uk)为系统状态的先验概率密度分布函数,其表达形式如式(2)所示
| $ \begin{array}{l} \;\;\;\;\;p\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{m}}_k}\left| {{z_{k - 1}}, {\mathit{\boldsymbol{u}}_k}} \right.} \right) = \\ \int {p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{x}}_{k - 1}}} \right., {\mathit{\boldsymbol{u}}_k}} \right)p\left( {{\mathit{\boldsymbol{x}}_{k - 1}}\left| {{z_{k - 1}}, {\mathit{\boldsymbol{u}}_{k - 1}}} \right.} \right)} {\rm{d}}{\mathit{\boldsymbol{x}}_{\mathit{k}{\rm{ - 1}}}}。\end{array} $ | (2) |
将式(2)代入到式(1)中可以得到后验概率密度分布为
| $ \begin{array}{l} \;\;\;\;\;\;p\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{m}}_k}\left| {{z_k}, {\mathit{\boldsymbol{u}}_k}} \right.} \right) = \\ \eta p\left( {{z_k}\left| {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{m}}_k}} \right.} \right)\int {p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{x}}_{k - 1}}} \right., {\mathit{\boldsymbol{u}}_k}} \right)} \times \\\;\;\;\ p\left( {{\mathit{\boldsymbol{x}}_{k - 1}}, {\mathit{\boldsymbol{m}}_{k - 1}}\left| {{z_{k - 1}}, {\mathit{\boldsymbol{u}}_{k - 1}}} \right.} \right){\rm{d}}{\mathit{{x}}_{\mathit{k}{\rm{ - 1}}}}, \end{array} $ | (3) |
其中p(xk|xk-1,uk)为系统的运动模型,p(zk|xk,mk)为系统的观测模型,这样如果前一时刻的状态已知的情况下就可以通过这2个模型就递推地得到下一时刻状态的后验概率估计。
2 FastSLAM算法为了避免计算上面的式(3)中的积分项,提高计算效率,需要对式(3)进行简化处理。由于SLAM问题满足一阶隐马尔可夫特性,并且如果确切的知道机器人的路径的时候,机器人对各个路标之间的观测是相互条件独立的。因此,Montemerlo等人提出了FastSLAM方法,采用Rao-Blackwellise因式分解的方法将后验概率分解为机器人路径的估计与地图估计的乘积的形式,将2者分离开来计算,提高了效率。其中采用粒子滤波器对机器人的路径进行估计,采用扩展卡尔曼滤波器对地图更新[8-9]。通过Rao-Blackwellise方法将式(3)转化为下式
| $ \begin{array}{l} \;\;\;\;\;\;p\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{m}}_k}\left| {{z_k}, {\mathit{\boldsymbol{u}}_k}} \right.} \right) = \\ p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{z_k}} \right., {\mathit{\boldsymbol{u}}_k}} \right)p\left( {{\mathit{\boldsymbol{m}}_k}\left| {{\mathit{\boldsymbol{x}}_k}, {z_k}, {\mathit{\boldsymbol{u}}_k}} \right.} \right) = \\ p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{z_k}, {\mathit{\boldsymbol{u}}_k}} \right.} \right)\prod\limits_{n = 1}^M {p\left( {{\mathit{\boldsymbol{m}}_{k, n}}\left| {{\mathit{\boldsymbol{x}}_k}, \left| {{z_k}} \right., {\mathit{\boldsymbol{u}}_k}} \right.} \right)}, \end{array} $ | (4) |
其中p(xk|zk,uk)描述的是对机器人的当前位姿状态的估计,
从公式(4)可以看出后验概率就可以看成对机器人的状态估计与对M个路标估计的M+1个滤波器的组合。FastSLAM方法中为了消除由于系统的运动模型以及观测模型的不确定性以及各种噪声误差导致的非线性,采用粒子滤波器对机器人的位姿进行估计。粒子滤波器方法主要是依据初始分布在机器人的状态空间中生成一批初始粒子集xk0,并且对于每个粒子赋予相等的权值wk0,然后利用最新得到的传感器观测信息与基于观测模型得到的预测信息的差值,不断更新粒子值以及相应的权值,从而最终利用粒子与相应的权值的代数和实现对机器人的定位。因此以样本集合的方法逼近概率分布的粒子滤波器定位方法就成为了一个重要的SLAM解决方法,并且理论上证明当粒子数趋近于无穷大时,样本集合可以逼近任何形式的概率分布。
但是FastSlAM算法随着迭代次数增加,粒子的权值往往会集中在少数粒子中,从而降低了粒子多样性。并导致粒子匮乏,使得计算效率降低,定位精度也受到影响。传统算法只能通过增加粒子数来解决这一问题,从而增加了计算的时间复杂度。
3 基于改进粒子滤波器SLAM方法 3.1 人工鱼群算法简介人工鱼群算法是通过模拟鱼群的觅食行为来进行寻优的[14]。主要包括觅食,聚群,追尾3个行为。对鱼群算法中的变量做出如下定义,人工鱼群状态变量为Xi,当前所在位置对应的食物浓度为Yi=g(Xi),算法中Yi越大说明状态越好,人工鱼的感知范围为Visual,移动步长为Step,拥挤度因子为δ。
1) 觅食行为
在满足|X-Xi| < visual中随机选择一个可以感知的邻域状态Xj,如果Yj > Yi,则利用式(5)更新鱼群状态;否则随机移动一步。
| $ {\mathit{\boldsymbol{X}}_i} = {\mathit{\boldsymbol{X}}_i} + \frac{{{\rm{random}}\left( {{\rm{step}}} \right)\left( {{\mathit{\boldsymbol{X}}_j} - {\mathit{\boldsymbol{X}}_i}} \right)}}{{\left| {{\mathit{\boldsymbol{X}}_j} - {\mathit{\boldsymbol{X}}_i}} \right|}}。$ | (5) |
2)聚群行为
设满足|X-Xi| < visual的X的个数为nf(非零),以及这些状态向量的几何中心位置为Xc。如果满足Yc/nf > δYi,则按照式(6)更新鱼群状态;否则执行觅食行为。
| $ {\mathit{\boldsymbol{X}}_i} = {\mathit{\boldsymbol{X}}_i} + \frac{{{\rm{random}}\left( {{\rm{step}}} \right)\left( {{\mathit{\boldsymbol{X}}_\mathit{c}} - {\mathit{\boldsymbol{X}}_i}} \right)}}{{\left| {{\mathit{\boldsymbol{X}}_c} - {\mathit{\boldsymbol{X}}_i}} \right|}}。$ | (6) |
3) 追尾行为
对满足|X-Xi| < visual的X中选取拥有最大食物浓度Ymax的伙伴Xmax。如果满足Ymax/nf > δYi,则按照式(7)更新鱼群状态;否则执行觅食行为。
| $ {\mathit{\boldsymbol{X}}_i} = {\mathit{\boldsymbol{X}}_i} + \frac{{{\rm{random}}\left( {{\rm{step}}} \right)\left( {{\mathit{\boldsymbol{X}}_{\max }} - {\mathit{\boldsymbol{X}}_i}} \right)}}{{\left| {{\mathit{\boldsymbol{X}}_{\max }} - {\mathit{\boldsymbol{X}}_i}} \right|}}。$ | (7) |
然后比较3种行为得到的状态向量对应的食物浓度值,将具有最大食物浓度的状态作为新的状态,然后重复执行,直到满足收敛条件为止。
3.2 基于人工鱼群算法的机器人位姿更新因此,只要合理的选择用于表示食物浓度的函数,在这里也可以称作适应度函数,就可以使得粒子在人工鱼群行为的作用下朝真实的粒子分布方向进化。选用实际观测值与预计观测值之间的差异大小来作为优化指标,故适应度函数为
| $ g\left( {{z_k}, {\hat z_k}} \right) = \prod\limits_{i = 1}^{{N_k}} {\exp (} - {\rm{sqrt}}\left( {{{\left( {z_k^i - \hat z_k^i} \right)}^2}/{{\boldsymbol{R}}_k}} \right)。$ | (8) |
其中zki为第i个路标在k时刻的实际观测值,
重采样方法最早是1993年由Gordon在文献[16]中提出的,其基本思想是基于样本的权重大小,去除小权值的粒子,保留大权值的粒子,从而可以在一定程度上提高粒子滤波器的性能。
重采样算法的实现是基于逆变法的思想。逆变法是以概率积分变换定理为基础的,假定连续随机变量X的分布函数为F(x)∈(0,1),且其反函数为F-1(u),其中u∈(0,1)。若U为[0, 1]均匀分布随机变量,则随机变量X=F-1(U)同X具有相同的分布函数。
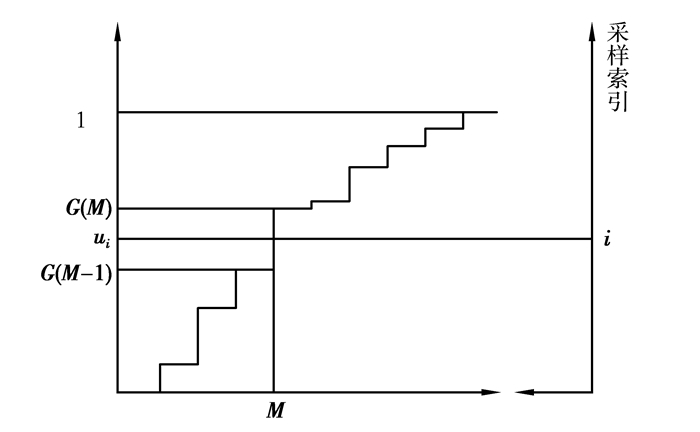
从均匀分布[0, 1]中随机生成样本ui,并且令
| $ G\left( {M - 1} \right) < {u_i} \le G\left( M \right) $ | (9) |
由此可见重采样的策略就如图 1所示。
|
图 1 重采样策略 |
从以上的分析可以看出传统的重采样方法由于是采用随机的方式,因此对粒子的退化现象几乎无能为力,大权值的粒子将会多次被复制,而低权值的粒子则会被去掉,这样这些粒子所代表的路径和地图信息将会被删除,从而失掉一些对于过去信息的了解。另一方面,大权值粒子被多次复制,许多子代粒子继承了相同的路径和地图估计,这使得粒子多样性大大降低。最终可能引起“粒子耗尽”问题,使得算法只能在短时间内满足一致性要求。
在人工鱼群算法中为了保证鱼群中的最优个体能够存活于子代中,从而将每一代中的最优个体保存到公告板中,然后与经过鱼群行为的下一代中的鱼群最优个体比较,如果公告板中的个体较优则用公告板中个个体代替下一代中最差个体;否则,将下一代的最有个体放入公告板中。
借鉴公告板的思想,提出了一种新的定向重采样方法,即首先保留每一步中权值最大的粒子进入公告板,如果需要进行重采样时,将依据权值的大小去除一半权值小的粒子,然后通过式(10)对公告板中的粒子进行预估操作用于代替去掉的粒子;然后对剩余的粒子按照权值的大小进行重采样。
| $ {{\boldsymbol{\hat{x}}}_{k}}{\rm{ = }}\mathit{\boldsymbol{x}}_{k - 1}^{公告} + \left( {\mathit{\boldsymbol{X}}_k^w - \mathit{\boldsymbol{X}}_{k - 1}^w} \right) + {\mathit{\boldsymbol{w}}_x}, $ | (10) |
式中Xkw为k时刻的加权后的位姿估计值,Xk-1w为k-1时刻的加权后的位姿估计值,wt为重采样估计噪声,并且满足均值为0的高斯分布。
Xkw-Xk-1w表示的就是对机器人在考虑噪声情况下施加的控制向量的最优估计,因此机器人经过重采样后既保持了样本的多样性,同时又使得粒子的分布更加接近真实状态,提高了性能。
3.4 算法实现设k时刻的机器人状态向量为xk=[Xk Yk θk],其中(Xk,Yk)为机器人在笛卡儿全局直角坐标系中的横纵坐标,θk为机器人的航向角,即机器人相对X轴的偏转角度,顺时针为负,逆时针为正。故可以得到实验中的机器人的运动学模型为
| $ \begin{array}{l} p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{x}}_{k - 1}}, {\mathit{\boldsymbol{u}}_k}} \right.} \right) = \left[\begin{array}{l} {X_k} + \Delta {D_k}\cos {\theta _k}\\ {Y_k} + \Delta {D_k}\sin {\theta _k}\\ \;\;\;\;{\theta _k} + \Delta {\theta _k} \end{array} \right] + {\mathit{\boldsymbol{w}}_k} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; f\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{u}}_k}} \right) + {\mathit{\boldsymbol{w}}_k}, \end{array} $ | (11) |
其中ΔDk为从k到k+1时刻机器人要走过的距离,Δθk为从k到k+1时刻机器人航向角的变化量,wk为运动模型噪声向量,并且满足均值为0的高斯分布。
一般通常采用机器人到路标的距离和路标与机器人的航向角的偏差角度值来描述测量值,则在k时刻机器人的量测方程为
| $ \begin{array}{l} Z_k^i = h\left( {\rho _k^i, \alpha _k^i} \right) = \\ \left[\begin{array}{l} \sqrt {{{\left( {{X_\mathit{k}}-X_{lk}^i} \right)}^2} + {{\left( {{Y_\mathit{k}}-Y_{lk}^i} \right)}^2}} \\\;\;\;\;\;\;\;\; \arctan \frac{{{Y_\mathit{k}}-Y_{lk}^i}}{{{X_\mathit{k}} - X_{lk}^i}} - {\theta _k} \end{array} \right] + {v_k}, \end{array} $ | (12) |
其中(Xlki,Ylki)为k时刻的机器人第i个路标的笛卡尔坐标位置,vk为观测噪声向量,并且满足均值为0的高斯分布。
综上,改进的粒子滤波SLAM方法的流程如下
Step1:粒子初始化:基于环境信息,生成k=0时刻初始粒子的位姿向量{x0i},并且平均分配粒子权值w0i=1/N,i=1,2,…,N,N为粒子个数;
Step2:位姿第一步预测:通过机器人的运动模型得k到时刻每个粒子的预估位姿{xk|k-1i};
Step3:通过传感器获得到k时刻真实观测值,采用最近邻方法进行数据关联,并且利用公式wki=wk-1ip(zki|xk|k-1i)更新粒子权值,然后用公式
Step 4通过人工鱼群算法对机器人的位姿进行二步预测:将粒子集{xk|k-1i}作为初始人工鱼群,利用如式(4)所示的适应度函数对鱼群中的个体分别进行觅食、聚群和追尾行为,从而得到二次更新后的粒子集{xki};
Step5:根据更新后的粒子集的位姿信息进行地图更新,并依据Step3中的公式对权值进行更新和归一化;
Step6:计算有效粒子数
Step7:通过加权公式计算出粒子k时刻的位姿,如果还需要计算下一时刻的位姿,转到Step2;否则结束定位。
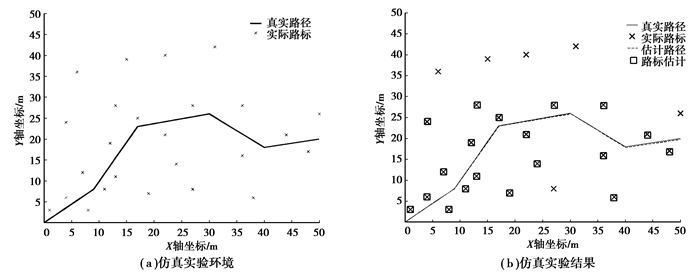
4 仿真实验与分析为了验证算法的正确性,利用matlab建立了如图 2(a)所示的仿真环境,大小为50 m×50 m,机器人能够在环境中自由移动,其中的黑色实线表示的就是机器人的真实运动轨迹,×表示的是实际的路标位置,相对于机器人是未知的。在仿真实验中机器人的最大移动速度设定为0.3 m/s,测距传感器所能检测到的最远距离为15 m,机器人横纵坐标位置方差为0.01 m,机器人航向角度方差为0.2°,路标的距离方差为0.01 m,角度方差为0.1°,粒子个数为10个。仿真的结果如图 2(b)所示,其中点画线表示的是对机器人路径的估计,□表示的是对路标的估计位置。可以看出改进后的方法能够对机器人位置和路标进行正确的估计。
|
图 2 仿真实验环境与结果 |
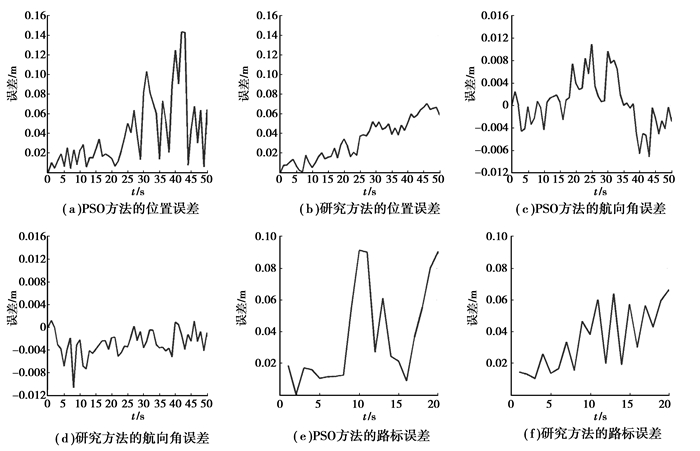
为了比较算法与文献[17]中基于粒子群优化(PSO)的改进粒子滤波器算法的性能,又在该仿真环境中采用相同的粒子数分别进行了仿真试验,得到的仿真结果如图 3(a)-(e)所示。
|
图 3 传统方法与改进方法误差比较 |
从图中可以看出提出的方法无论在位置估计精度,航向角估计精度与路标估计精度上都比PSO方法有了提高。其中,位置误差的均值由0.41 m减少到0.034 m,并且误差的波动也很小。航向角误差由0.003 4 rad减少到0.003,路标误差由0.037减少到0.003 5。
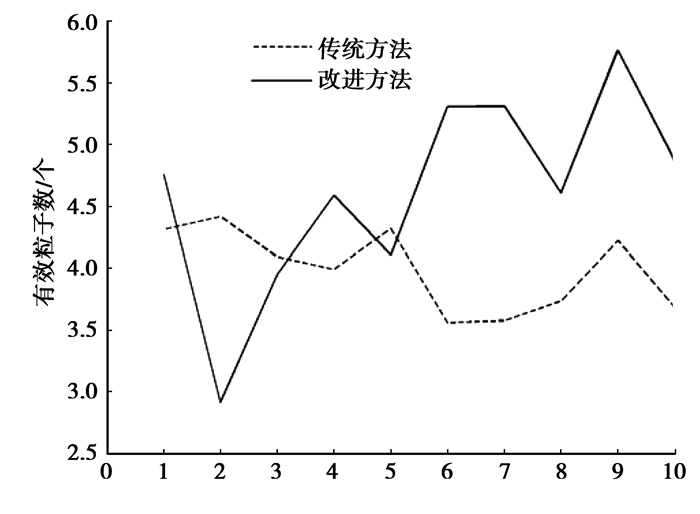
为了考察定向重采样方法对粒子退化现象的改善情况,对传统的重采样方法和本文所研究的方法分别运行10次,并计算2种算法的有效粒子数的平均值的变化情况,得到仿真结果如图 5所示。
|
图 4 有效粒子数的比较 |
可以看出所提出的定向重采样方法能够得到更多的有效粒子数,有效粒子数的平均值由0.336提升到4.616,从而较好地改善粒子的退化现象。同时为了验证研究方法对粒子贫化现象的改善情况,通过比较2种方法产生的粒子平均海明距离来表示2种方法的粒子多样性。仿真结果如表 1所示,改进的重采样方法的多样性平均值由0.336提升为0.978,能在很大程度上提高粒子的多样性。
| 表 1 2种方法多样性比较结果 |
笔者提出了一种基于改进粒子滤波器的SLAM方法,利用了人工鱼群算法的三种鱼群行为对通过运动模型产生的预估粒子进行了二次更新,并采用定向重采样的方法使得粒子的多样性得到了提高,同时也增加了有效粒子数。仿真实验结果证明了方法的合理性。
| [1] |
王勇, 朱华, 王永胜, 等.
煤矿救灾机器人研究现状及需要重点解决的技术问题[J]. 煤矿机械, 2007, 28(4): 107–109.
WANG Yong, ZHU Hua, WANG Yongsheng, et al. Current status and technical problems in research of coal mine rescue robot[J]. Coal Mine Machinery, 2007, 28(4): 107–109. (in Chinese) |
| [2] | Kortenkamp D, Bonasso R P, Murphy R. AI-based mobile robots:case studies of successful robot systems[M]. Cambridge: MIT Press, 1998. |
| [3] |
戴珊珊, 董伟伟.
煤矿环境探测机器人航位研究[J]. 煤矿机械, 2010, 31(9): 49–50.
DAI Shanshan, DONG Weiwei. Air spaces research of coal mine environment detection robot[J]. Coal Mine Machinery, 2010, 31(9): 49–50. (in Chinese) |
| [4] | Daum F. Nonlinear filters:beyond the Kalman filter[J]. IEEE Aerospace and Electronic Systems Magazine, 2005, 20(8): 177–183. |
| [5] | Dissanayake G, Newman P, Clark S, et al. A solution to the simultaneous localization and map building(SLAM) problem[J]. IEEE Transactions on Robotics and Automation, 2001, 17(3): 229–241. DOI:10.1109/70.938381 |
| [6] | Holmes S A, Klein G, Murray D W. An O(N2) square root unscented Kalman filter for visual simultaneous localization and mapping[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(7): 1251–1263. DOI:10.1109/TPAMI.2008.189 |
| [7] |
余洪山, 王耀南.
基于粒子滤波器的移动机器人定位和地图创建研究进展[J]. 机器人, 2007, 29(3): 281–297.
YU Hongshan, WANG Yaonan. A review on mobile robot localization and map-building algorithms based on particle filters[J]. Robot, 2007, 29(3): 281–297. (in Chinese) |
| [8] | Montemerlo M, Thrun S, Koller D, et al. FastSLAM:A factored solution to the simultaneous localization and mapping problem[C]//Proceedings of the National Conference on Artificial Intelligence, July 28-August 1, 2002, Cambridge, MA, USA. Massachusetts:MIT Press, 2002:593-598. |
| [9] | Montemerlo M, Thrun S, Koller D, et al. FastSLAM 2.0:An improved particle filtering algorithm for simultaneous localization and mapping that provably converges[C]//Proceedings of the International Conference on Artificial Intelligence, August 9-15, 2004, Acapulco, Mexico. Piscataway:IEEE Press, 2003:1151-1156. |
| [10] | Dong J F, Wijesoma W S, Shacklock A P. An efficient rao-blackwellized genetic algorithmic filter for SLAM[C]//Proceedings of 2007 IEEE International Conference on Robotics and Automation, April 10-14, 2007, Roma, Italy. Piscataway:IEEE Press, 2007:2427-2432. |
| [11] | Lee H C, Park S K, Choi J S. PSO-FastSLAM:An improved fastSLAM framework using particle swarm optimization[C]//Proceedings of the 2009 IEEE International Conference on Systems, Man, and Cybernetics, October 11-14, 2009, San Antonio, TX, USA. Piscayaway:IEEE Press, 2009:2763-2768. |
| [12] | Chatterjee A, Matsuno F. Improving ekf-based solutions for SLAM problems in mobile robots employing neuro-fuzzy supervision[C]//Proceedings of 2006 Third IEEE International Conference on Intelligent Systems, September 4-6, 2006, London, UK. Piscataway:IEEE Press, 2006:683-689. |
| [13] |
厉茂海, 洪炳熔, 罗荣华.
用改进的Rao-Blackwellized粒子滤波器实现移动机器人同时定位和地图创建[J]. 吉林大学学报:工学版, 2007, 37(2): 401–406.
LI Maohai, HONG Bingrong, LUO Ruohua. Improved rao-blackwellized particle filters for mobile robot simultaneous localization and mapping[J]. Journal of Jilin University:Engineering and Technology Edition, 2007, 37(2): 401–406. (in Chinese) |
| [14] |
李晓磊, 邵之江, 钱积新.
一种基于动物自治体的寻优模式:鱼群算法[J]. 系统工程理论与实践, 2002, 22(11): 32–38.
LI Xiaolei, SHAO Zhijiang, QIAN Jixin. An optimizing method based on autonomous animats:fish-swarm algorithm[J]. System Engineering Theory and Practice, 2002, 22(11): 32–38. DOI:10.3321/j.issn:1000-6788.2002.11.007 (in Chinese) |
| [15] | Smith R C, Cheeseman P. On the representation and estimation of spatial uncertainty[J]. The International Journal of Robotics Research, 1986, 5(4): 56–58. DOI:10.1177/027836498600500404 |
| [16] | Gordon N J, Salmond D J, Smith A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings F Reader and Signal Processing, 1993, 140(2): 107–113. DOI:10.1049/ip-f-2.1993.0015 |
| [17] | Zhang G Y, Cheng Y M, YangF, et al. Particle filter based on PSO[C]//Proceedings of 2008 International Conference on Intelligent Computation Technology and Automation, October 20-22, 2008, Hunan, China.Piscataway:IEEE Press, 2008, 1:121-124. |
 2014, Vol. 37
2014, Vol. 37


