2. 广西民族大学 信息科学与工程学院, 南宁 530006
2. College of Information Science and Engineering, Guangxi University for Nationalities, Nanning 530006, China
基于概率的子空间方法是人脸识别算法中的一种重要方法,尽管出现了很多其他识别方法如SVM,但子空间方法仍然受到研究者的关注,并有着广泛的应用前景。典型代表有PCA[1-2], LDA[3-5]等, 以及将它们与核方法结合而得到的KPCA[6], KLDA[7]等, 也有人将其与小波、神经网络等相结合得到一些较好的结果。但这其中最基本的仍然是PCA算法,其他算法如LDA、Bayes由于自身计算复杂度等原因,一般都是先运行PCA得到相应的特征空间,然后在此特征空间上运行这些算法。目前关于PCA研究主要集中2个方面,一方面是PCA理论研究[8-9],针对特征向量的生成方法,特别是奇异值分解(SVD),希望能用尽可能少的特征向量代表更多的数据信息。另一方面是利用PCA进行维数约简和特征抽取,在模式识别中,由于识别对象维数往往很高(图像),为了提高识别速度必须进行维数约简。PCA进行维数约简时,它将作用对象(图像)从高维数据空间(如256×256=65536)压缩到指定维数(20),虽然在压缩过程中会丢失一些信息,但一般认为这些信息是不太重要的较小数据。但一些研究表明这部分丢弃的数据仍然含有部分分类信息,由于数据过度集中且在产生PCA特征空间时没有考虑分类信息,使得直接在PCA特征空间进行分类识别效果并不理想。在PCA空间上的LDA、Bayes等方法就是希望结合分类信息来提高识别质量。而KPCA则是利用核技术将低维映射到高维空间以此来提高特征空间所含的分类信息。提出一种新的融合分类信息和维数约简的带权稀疏PCA(WSPCA)方法,该方法根据分类信息对PCA特征空间中的特征值进行修正,并利用SPCA方法进行维数约简,使其含有更多的分类信息。在人脸数据库上的实验结果表明该方法能有效提高识别的正确率,并且有较快的计算速度。
1 算法基础以二维人脸识别为例,来说明算法的基本理论。2D人脸图像可被看成是图像空间的一个向量,人脸图像样本{xi}集合可以用一个N×M的矩阵X=[x1, …, xM],这里N是图像的象素点数,M是样本个数。每幅图像属于某一人脸类{X1,…,XL},l(xi)是xi的类标志。当要识别的对象被输入时,人脸识别的任务就是在数据库中找它的类标志。为了引出研究方法,这里首先介绍LDA算法及其导出方法。
1.1 LDA简介LDA希望寻找这样的一个子空间,它通过最大化类间分散矩阵Sb,最小化类内分散矩阵Sw,来最大化不同类的差异度。Sb和Sw定义如下:
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}_w} = \sum\nolimits_{i = 1}^L {\sum\nolimits_{{x_{ki}}} {\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{m}}_i}} \right){{\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_i}} \right)}^{\rm{T}}}} } \\ \;\;\;{\mathit{\boldsymbol{S}}_b} = \sum\nolimits_{i = 1}^L {{\mathit{n}_i}\left( {{\mathit{\boldsymbol{m}}_i} - m} \right){{\left( {{\mathit{\boldsymbol{m}}_i} - m} \right)}^{\rm{T}}}} \end{array} $ |
这里,mi是个体Xi类的平均脸,ni是类Xi的样本数。
LDA子空间由满足下列条件的向量W所张成的空间。
| $ W = \arg \max \left| {\frac{{{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_b}\mathit{\boldsymbol{W}}}}{{{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{W}}}}} \right|, $ | (1) |
所以W能由Sw-1Sb的特征向量组成。计算的特征向量,等于同时对角化Sw和Sb。首先计算Sw的特征向量矩阵Φ和特征值矩阵Θ。然后,投影类中心到ΦΘ-1/2上。所以Sb转换为Kb=Θ-1/2ΦTSbΦΘ-1/2。然后,计算Kb的特征向量矩阵Ψ和特征值矩阵Λ,LDA的投影向量为:W=ΦΘ-1/2Ψ。识别时,线性判别函数定义为
d(T)=WT(T-P)。
选择使‖d‖最小的类作为待识别人脸所属的类。
从上面的LDA特征向量的计算过程可以看出,LDA它的本意是针对原始训练样本空间的,希望得到一个与PCA算法一样的一组特征向量,然后用这组得特向量将原始数据转换到特征子空间来,从而达到在维数约简的同时使得类内间的距离尽可能近,而类间距离尽可能远目的。但由于Sw和Sb的维数一般都比较高,使得直接用在原始人脸数据集上比较困难,且可能遇到对奇异矩阵求逆的困难,因此一般先通过PCA算法获取PCA特征空间,然后在此空间上运行LDA算法。由于PCA子空间在获取时已经略去了部分信息,因此,人们指出零子空间的存在并研究出了一些消去零子空间的方法,也有些研究者,直接作用于原始人脸数据的LDA算法[10],并且取得了较好结果。
1.2 PCA特征空间维数约简在具体应用中,由于PCA算法将学习对象所携带的信息80%以上集中到对应的特征值大的几个特征向量上,特征值较小的部分由一些对识别有用的信息和噪声组成,一般情况下,可以认为5%最小特征值对应噪声,在去除5%最小特征值所对应的特征向量后,剩下的95%的相对较大的特征值对应的特征向量组成的矩阵作为映射,这样可充分利用原始学习样本所携带的有利于识别的信息。但带来的问题是用来作为映射的特征向量的个数变得较多。特别是,当用于学习的样本较多时,对识别速度有较大影响,为此有必要进一步降低维数,即减少用于作为映射的特征向量个数。这方面工作也有不少研究成果,如ScotLass[11]法、SPCA[9]法、最新的成果是文献中提出的非负装载方法来求解主成份[12]。这里选择SPCA(sparse principal component analysis)法来实现PCA子空间的维数约简。为此在下面简要介绍SPCA技术。
PCA寻求的是获得最大方差的原始变量的线性组合,PCA可以通过已中心化的数据矩阵X的奇异值分解(SVD)实现。X的SVD分解可表示为
| $ \mathit{\boldsymbol{X = }}\mathit{UD}{\mathit{\boldsymbol{V}}^{\rm{T}}}。$ | (3) |
U为单位长度的主成份(PCs),V的列是主成份的相应的装载,第i个PC的方差是Di, i2,D=diag{d1, d2, …}。
一种直接sparse PCA方法可表述如下
| $ \hat \beta = \arg \mathop {\min }\limits_\beta \{ {\left| {{Y_i} - X\beta } \right|^2} + \lambda {\left| \beta \right|^2} + {\lambda _1}\left| {{\beta _1}} \right|\}, $ | (4) |
文献[9]同时提出了一种自含式sparsePCA算法,记为SPCA。该算法初始化α=V[1:k];对每个j=1, 2, …, k,求解下式
| $ \begin{array}{l} {\beta _j} = \arg \mathop {\min }\limits_{{\beta ^*}} {\mathit{\boldsymbol{\beta }}^{\mathit{\boldsymbol{*}}{\rm{T}}}}\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} + \lambda } \right){\lambda ^*} - \\ \;\;\;\;\;2\mathit{\boldsymbol{\alpha }}_j^{\rm{T}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{\beta }}^\mathit{\boldsymbol{*}}} + {\lambda _{1, \mathit{j}}}{\left| {{\mathit{\boldsymbol{\beta }}^\mathit{\boldsymbol{*}}}} \right|_1}, \end{array} $ | (5) |
然后作XTXβ的SVD分解,记为UDVT,再让α=UVT,重复这个过程直至β收敛。最后令:
另外从(3)式,得XTX的特征分解:
| $ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} = V{D^2}{\mathit{\boldsymbol{V}}^{\rm{T}}}, $ | (6) |
称特征向量vj(V的列)为X的主成份(或Karhunen-Loeve)方向。第一个主成份方向v1满足:在所有的X列向量的规范化线性组合中,z1=Xv1有最大的样本方差,即
| $ {\rm{Var}}\left( {{\mathit{z}_1}} \right) = {\rm{Var}}\left( {\mathit{\boldsymbol{X}}{\mathit{v}_{\rm{1}}}} \right) = \frac{{d_1^2}}{N}。$ | (7) |
事实上
| $ {\mathit{z}_1} = \mathit{\boldsymbol{X}}{\mathit{v}_{\rm{1}}} = {u_1}{d_1}, $ | (8) |
由此导出变量z1称为X的第一个主成份,所以u1是第一个规范化主成份。
事实上,在利用PCA算法进行特征抽取时,所用的抽取矩阵(或转换矩阵)即为此处的V,它利用V作为转换算子将样本空间转换到PCA特征子空间。因此,在模式识别的特征抽取中,感兴趣的是PCA算法所得的V,上面介绍的sparse PCA算法在约简主成份空间维度的同时,也实现了对V的维度约简。但上述算法是针对整个V的维度约简,没有考虑去噪,为达到去噪作用,在执行上述SPCA算法之前,需要对X进行去噪预处理。即先对V执行PCA算法,得到其主成份装载向量V,按95%选取大特征值所对应的装载向量,其结果仍然记为V。利用式(6)和(8)可令式(4)中的Yi为:Yi=Xvi,然后利用直接sparse PCA方法求得相应的sparse V。但在式(4)、(5)中的X还是原有的含噪声数据,为了去除噪声对进一步估计的影响,需用去噪以后的V还原数据矩阵X。由前面的讨论可知
| $ {u_i} = \mathit{\boldsymbol{X}}{\mathit{u}_i}/{d_i}, $ | (9) |
从而可求出相应的主成份矩阵U,最后利用式X=UDVT求出X,此时的X可看成是已对原数据经过去噪处理的数据。最后用此X通过SPCA算法求得X即得特征抽取中所需要的转换矩阵V。
2 带权主成分分析分析LDA过程会发现,最初构造的类间分散矩阵Sb和类内分散矩阵Sw,完全是为了获最LDA特征向量W,但如果不是为了获取向量,构造这样的矩阵也就没有意义了。PCA特征空间已经是通过维数约简得到的,原始人脸数据信息已被集中在几个特征值上。再通过LDA进行二次维数约简反而使得特征值更加集中,从而使分类更加困难,这可能就是一些文献中提到的在某些情况下LDA的识别率还没有PCA高的原因所在。其实在得到PCA子空间后,只需将各特征值中有利于增大类间距离而缩小类内距离的有用信息提取出来即可。即希望获得每个特征值中最有价值的部分,也即希望计算出每个特征值中最有价值的信息占总信息量的百分比。记这个百分比向量为u={u1, …, uK},满足:
| $ {\mathit{\boldsymbol{S}}_w} = \left( \mathit{\boldsymbol{u}} \right) = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {{{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2}\mathit{\boldsymbol{u}}_k^2;} } } $ | (10) |
| $ {\mathit{\boldsymbol{S}}_b}\left( \mathit{\boldsymbol{u}} \right) = \sum\limits_{i \ne j} {\sum\limits_{k = 1}^K {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}\mathit{\boldsymbol{u}}_k^2} }。$ | (11) |
目标是寻找使Sw(u)尽可能小,而Sb(u)尽可能大的u。为此,利用Lagrange乘子方法构造函数如下
| $ J\left( \mathit{\boldsymbol{u}} \right) = {\mathit{\boldsymbol{S}}_w}\left( \mathit{\boldsymbol{u}} \right) - {\lambda _1}{\mathit{\boldsymbol{S}}_b}\left( \mathit{\boldsymbol{u}} \right) + {\lambda _2}\left( {\sum\limits_{k = 1}^K {{\mathit{\boldsymbol{u}}_k}} - 1} \right)。$ | (12) |
将式(10)、(11)代入式(12)可得
| $ \begin{array}{l} J\left( \mathit{\boldsymbol{u}} \right) = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {{{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2}\mathit{\boldsymbol{u}}_k^2 - } } } {\lambda _1}\sum\limits_{i \ne j} {\sum\limits_{k = 1}^K {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}\mathit{\boldsymbol{u}}_k^2} } + {\lambda _2}\left( {\sum\limits_{k = 1}^K {{\mathit{\boldsymbol{u}}_k}} - 1} \right){\rm{ = }}\\ \;\;\;\;\;\;\;\sum\limits_{k = 1}^K {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2}\mathit{\boldsymbol{u}}_k^2 - } } } {\lambda _1}\sum\limits_{k = 1}^K {\sum\limits_{}^{i \ne j} {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}\mathit{\boldsymbol{u}}_k^2 + } } {\lambda _2}\left( {\sum\limits_{k = 1}^K {{\mathit{\boldsymbol{u}}_k}} - 1} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^K {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2} - } } {\lambda _1}\sum\limits_{i \ne j} {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}\mathit{\boldsymbol{u}}_k^2 + } {\lambda _2}\left( {\sum\limits_{k = 1}^K {{\mathit{\boldsymbol{u}}_k}} - 1} \right)。\end{array} $ | (13) |
对式(13)两边关于uk, k=1, …, K, 求导并令其为零得
| $ 2\left( {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2} - {\lambda _1}\sum\limits_{i \ne j} {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}} } } } \right){\mathit{\boldsymbol{u}}_\mathit{k}} + {\lambda _2} = 0, k = 1, \cdots, K。$ | (14) |
从而有
| $ {\mathit{\boldsymbol{u}}_\mathit{k}}{\rm{ = }}\frac{{{\rm{ - }}{\lambda _2}}}{{2\sum\nolimits_{i = 1}^M {\sum\nolimits_{j = 1}^N {{{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2} - } {\lambda _1}\sum\nolimits_{i \ne j}^{} {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}} } }}, k = 1, \cdots, K。$ | (15) |
考虑到λ2与k值无关,且在识别过程中可以将公因子提取出来,其取值不影响识别,为此为妨取λ2=-2。所以式(15)可简化为
| $ {\mathit{\boldsymbol{u}}_\mathit{k}}{\rm{ = }}\frac{1}{{\sum\nolimits_{i = 1}^M {\sum\nolimits_{j = 1}^N {{{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2} - } {\lambda _1}\sum\nolimits_{i \ne j}^{} {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}} } }}, k = 1, \cdots, K。$ | (16) |
由于0<uk<1, k=1, …, K,不妨设
| $ {\mathit{\boldsymbol{u}}_\mathit{k}}{\rm{ = }}\left| {\frac{1}{{\sum\nolimits_{i = 1}^M {\sum\nolimits_{j = 1}^N {{{\left( {{x_{i, j, k}} - {m_{i, k}}} \right)}^2} - } {\lambda _1}\sum\nolimits_{i \ne j}^{} {{{\left( {{m_{j, k}} - {m_{i, \mathit{k}}}} \right)}^2}} } }}} \right|, k = 1, \cdots, K。$ | (17) |
再根据
| $ \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{u}}_\mathit{k}}} = 1, $ | (18) |
可求得λ1,并代入式(17)即可求得所有uk, k=1, …, K。
求出uk, k=1, …, K后,可以利用它从PCA特征子空间中分离出所需要的分类信息。由于u要作用于PCA特征子空间的所有元素,所以不防将u整合到PCA的转换矩阵中。设PCA的转换矩阵为G={g1, …, gK},与u整合后得:G′={u1g1, …, uKgK},为方便其见,仍记为G。在进行具体识别时式(2)就变成了
| $ d\left( \mathit{\boldsymbol{T}} \right) = {\mathit{\boldsymbol{G}}^{\rm{T}}}\left( {\mathit{\boldsymbol{T}} - \mathit{\boldsymbol{P}}} \right), $ | (19) |
因此,结合所介绍的维数约简方法,可得稀疏带权PCA算法(WSPCA),该算法对给定的训练集,可按给定的维数要求求出相应的转换矩阵G。具体算法描述如下
算法weighted sparse principal component analysis(WSPCA)
Input:
X //training data set
M //the number of individual
N //the number of training sample per individual
K //the number of eignvectors in sparsePCA
Output:
G //the transformation matrix of WSPCA
1)(V,D)=PCA(X,M,N,95%); //calculating the 95% eignvetors and eignvalues of XTX
2) ui=Xvi/di//computing the principal components of matrix X
3) X=UDVT // denoising
4G′=SPCA(X, K)//computing the trsformation matrix of SPCA
5) Y=G′X;//computing PCA subspace
6) mi=mean(Yi), i=1, …, M//computing the mean of every class
7) compute uk, k=1, …, K//where K is columns of G
8) gi=ui×gi, i=1, …, K//where G=[g1, …, gK]
9) output G
上述算法中,除第4步外,每步都可以通过直接计算得到所需要的结果,因此算法是收敛的,由于算法第4步所得G′中的列向量是正交向量序列,由第7步计算出的uk是一常量,因此最后输出的G的列向量也是正交向量序列。
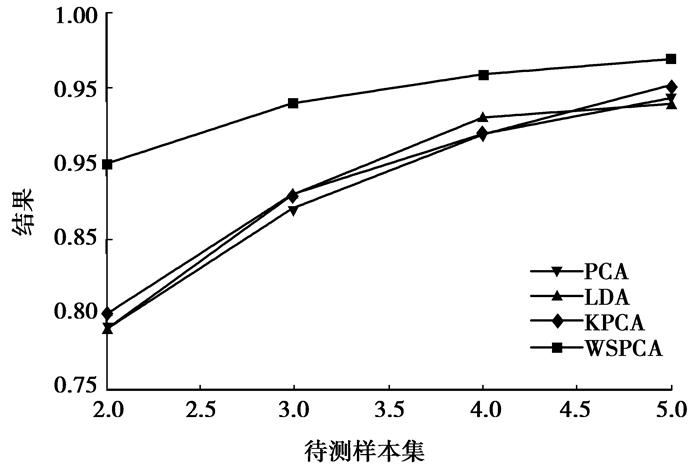
3 应用举例 3.1 在UIC[13]数据库上新算法的测试情况将待测样本集分为7个待测集,分别是不带墨镜下的除训练样本外的3种表情和带墨镜下的所有4种表情,分别用算法PCA、LDA、KPCA、WSPCA在总特征空间大小为15、20、25、30的情况下进行测试,测试结果如图 1所示。
|
图 1 UIC数据库上新算法的测试 |
由于F_JDLDA算法的特征空间大小由算法自身根据学习情况设定,在本例中该算法自动设定特征空间大小为15,其识别率仅为70%。从上图可以看出,在总特征空间大小分别为15、20、25、30 4种情况下,所提出的算法与另外4种算法相比有更好的识别率,特别是当有较小的特征空间时,越显出所提出算法的优越性。当特征空间逐渐变大时各方法的识别率趋于一致,但所提算法还是比其他算法的识别率高。
3.2 在AR数据库上新算法的测试情况为了进一步说明WSPCA算法的可行性,在AR数据库上进行实验。为此先对AR数据库中的图片进行简单的预处理。将原RGB图片转换成YcBcR彩色模型,利用肤色确定人脸位置,再从上面和左右3个方向向中间搜索按同一大小确定脸部位置矩形,再将该位置矩形中的脸部取出转换成灰度值图像并按2:1压缩存贮。没有按眼睛位置进行对准及旋转处理。在本次实验中对上述4种算法按不同的训练样本数和不同的个体数进行比较,所得结果如图 2和图 3所示,从实验结果来看提出的算法是有效的。
|
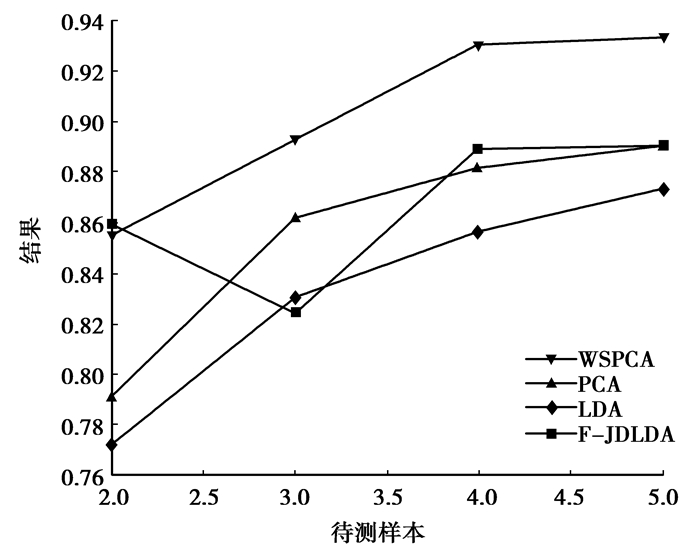
图 2 5男5女个体随训练样本数的变化识别率 |
|
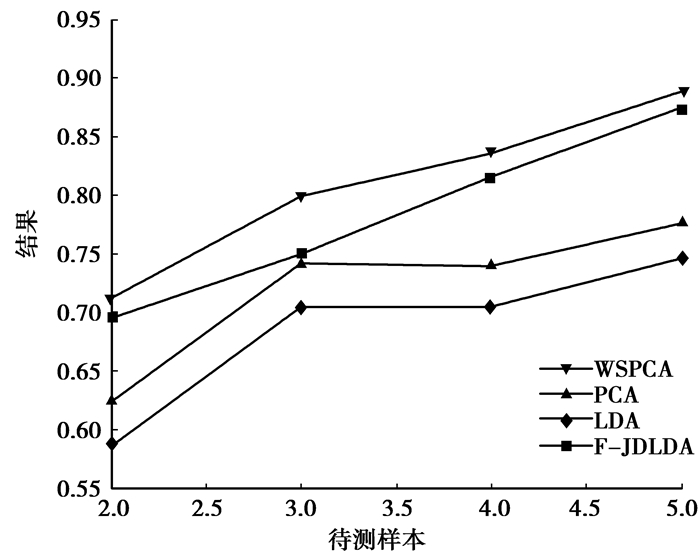
图 3 10男10女随训练样本数的变化识别率 |
图 2描述了针对5男5女共10个个体随各个体训练样本数的变化识别率的变化情况,从图 2中看出,WSPCA、PCA、LDA 3个算法的识别率随训练样本数的增加而稳步增加,但F-JDLDA算法却波动很大,当各个体训练样本只有2个时它是最好的,但当各个体训练样本有3个时它的识别率反而降低。但总的来说,当各个体训练样本大于等于3时,可以看出所提新算法相对于其他3种算法有较强的优势。图 3描述了针对10男10女共20个个体随各个体训练样本数的变化识别率的变化情况,从图 3中看出,在这种情况下,F-JDLDA算法随个体训练样本数增加稳步上升,反而PCA、LDA有小部分波动,同时可以看出所提新算法相对于其他3种算法有较好的识别率。且从2种情况下,所提新算法WSPCA都有较好的稳定性,其识别率随个体训练样本数增加稳步上升。
4 结论模式识别中的PCA算法所得的特征子空间没有提供过多的分类信息,且为了约简维数,省略了小特征值所对应的特征向量,而这部分特征向量同样也含有相当多的分类信息。为了达到去噪、维数约简和增强特征子空间的分类信息,提出算法WSPCA将PCA算法、SPCA算法、LDA算法有效地揉合到一起,利用PCA算法达到去噪作用,利用SPCA算法达到维数约简效果,利用LDA算法的基本思想完成可分功能。从实验效果看,所提出的算法有较好的正确识别率和稳定性。下一步工作,可以从2个方面继续研究,一是探索更好的维数约简方法,二是将该算法推广到三维模式识别和其他具体应用中。
| [1] | Turk, Pentland. Eigenfaces for ecognition[J]. Journal of Cognitive Neuroscience, 1991, 3(1): 71–86. DOI:10.1162/jocn.1991.3.1.71 |
| [2] | Zafeiriou, Petrou. Nonlinear on-egative omponent nalysis lgorithms[J]. IEEE ransactions on mage processing, 2010, 19(4): 1050–1066. DOI:10.1109/TIP.2009.2038816 |
| [3] | Zhao Y. Incremental inear criminant nalysis for ace ecogntion[J]. IEEE ransactions on ystems, an, and yberneticsart:ybernetics, 2008, 38(1): 210–221. |
| [4] | Cai. SRDA:n fficient lgorithm for arge-cale iscriminant nalysis[J]. IEEE ransactions on nowledge and ata nginering, 2008, 20(1): 1–12. |
| [5] | Zhu. Subcss icriminant nalysis[J]. IEEE ransactions on attern nalysis and aching ntelligence, 2006, 28(8): 1274–1286. |
| [6] | Suter. Incremental ernel rincipal omponent nalysis[J]. IEEE ransactions on mage rocessing, 2007, 16(6): 1662–1674. DOI:10.1109/TIP.2007.896668 |
| [7] | Liu Q S, Huang R, Lu H Q. Face recognition using kernel based fisher discriminant analysis[C]//Proceedings of International Conference on Automatic Face and Gesture Recognition, Washington:IEEE, 2002:197-201. |
| [8] | Zou, Hastie. Regularization and variable selection via the elastic net[J]. Journal of Royal Statistic Society Series B, 2005(67): 301–320. |
| [9] | Zou H, Hastie, Tibshirani. Sparse principal component analysis[J]. Journal of Computational and Graphical Statistics, 2006(15): 262–286. |
| [10] | Lu, Plataniotis, Venetsanopoulos. regularization tudies of inear iscriminant nalysis in mall ample ize cenarios with pplication to ace ecognition[J]. Pattern Recognition Letter, 2005, 26(2): 181–191. DOI:10.1016/j.patrec.2004.09.014 |
| [11] | Trendafilov, Jolliffe. DALASS:Variable selection in discrimininant analysis via the LASSO[J]. Computational Statistics & Data Analysis, 2007(51): 3718–3736. |
| [12] | Liipovetsky. PCA and SVD with nonnegative loading[J]. Pattern Recognition, 2009(42): 68–76. |
| [13] | Blake C, Keogh E, Merz C.UCI repository of machine learning database, 1998[EB/OL]. http://www.ics.uci.edu/mlearn/MLRepository.html, 1998. |
 2014, Vol. 37
2014, Vol. 37


