2. 重庆理工大学 计算机科学与工程学院, 重庆 400054
2. College of Computer Science and Engineering, Chongqing University of Technology, Chongqing 400054, China
对于人脸图像,人类能轻松地获取蕴藏其中的各种信息,如身份、性别、种族、大致的年龄及表情等。而让计算机也能达到人类对人脸的认知程度是相当困难的,尤其是对人脸年龄的自动估计,原因在于相对于其他的面部变化,年龄变化有其自身独特的性质。首先,人的年龄是不可控的,无法任意提前或延迟,是一个缓慢而不可逆的过程;其次,年龄对于不同人有着不同的变化模式,这不仅由内在的因素,如基因,种族等所决定,还受到诸如健康状况,生活方式,气候条件等外部条件的影响。年龄变化的上述特性不仅使得收集足够的带年龄信息的训练数据变得极其困难,而且也很难找到准确的刻画年龄变化的特征。但年龄估计及有年龄变化的人脸识别有着极其广泛的应用,因而寻求这类问题的解决方法也越发显得的重要。人脸图像中包含着年龄信息,但也有大量信息表达的是数据采集时的光照情况,人的表情和姿势等,这些信息不仅和年龄无关,还会对年龄的估计造成干扰,如何从人脸中提取能刻画年龄的特征,成为问题解决的关键。目前采用的人脸年龄估计的方法大致可以分为4类:
人体测量模式[1],通过对人脸外形及纹理模式的变化的测量,将人脸大致分类成几个年龄段,但不适合更为精细年龄划分的估计。
年龄变化模式子空间[2-3],收集测试对象的不同年龄阶段的人脸图像,需要确切知道训练集中每张人脸图像的身份信息,在许多实际应用中人脸的身份信息是不完备的,缺乏现实应用性。
年龄变化流行分析方法[4-5],通过流行学习算法模式化一个年龄变化的流行空间,在此流行中求一个低维特征的子流行作为训练样本的年龄变化结构的特征描述,能有效揭示人脸图像的流行结构特征,但仍然需要通过学习建立人脸年龄变化信息和低维特征之间的关系。
年龄回归方法[6-8],年龄回归方法将年龄估计视为多线性回归问题,目的是寻找合适的回归函数,以此描述人脸图像和年龄估计间的联系。该方法因简单高效,被许多人脸年龄估计系统所采纳。
笔者建议的梯度直方图(HOG)及局部二值化模式(LBP)都是人脸的灰度值差分后的统计特征描述子,具有光照和旋转不变性的优势,有效地抑制图像背景信息对年龄估计的干扰。HOG和LBP直方图分别从纹理均匀一致性及人脸灰度值的梯度方向直方图表示人脸的年龄变化特征,对于人脸年龄变化的信息互相提供了有益的补充。鉴于将人脸的外形特征[9]和纹理特征融合被[8]证明更能刻画人类年龄。利用典型相关分析(CCA)[10]方法融合局部二进制模式(LBP)直方图和梯度直方图(HOG)作为人脸的特征描述子,用支持向量机回归(SVR)结合留一交叉验证法(LOPO)的策略对塞浦路斯大学的人脸年龄库FG-NET[11]行训练和测试,取得较为满意的效果。
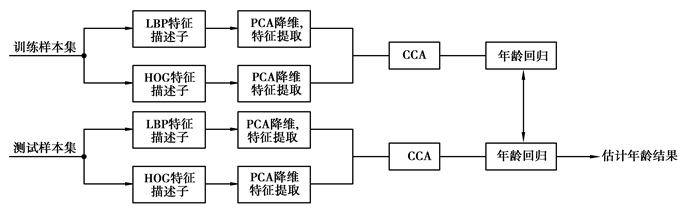
1 特征提取选择人脸图像的LBP和HOG特征描述开始,然后用PCA进行特征的提取,将提取的特征融合,最后选取分类器学习出年龄回归模式,并用该模式进行年龄的预测。流程图 1,展示了该方法对人脸年龄估计的过程。
|
图 1 年龄估计方法流程图 |
年龄变化特征提取,图像特征选取的一般原则是同类的图像差异较小(较小的类内距),不同类的图像之间有较大的差异(较大的类间距),即最具有区分力的特征。同时尽量减小特征提取的计算复杂度。随着年龄的增长,人脸变化最为突出的体现在局部区域,如眼角,嘴角等,局部二值模式(LBP)和梯度方向直方图(HOG)都是对与年龄变化密切相关的人脸图像灰度值差分统计。Déniz等[12]表明对人脸局部特征刻画非常有效,不仅有着光照及旋转不变性的优良特质,特征的提取的算法复杂度也较小。将人脸图像归一化成80×64的灰度图像,并划分成包含80个8×8窗口的网格,然后对每个小窗口提取LBP和HOG的直方图,最后将直方图分别连接起来形成直方图序列,作为人脸的LBP特征向量和HOG特征向量。
1.1 局部二值模式(LBP)LBP算子将人脸图像中的每个像素按3×3的领域像素相对中心像素的中心灰度值作二值化运算:每个像素以其灰度值fc为阈值,若周围像素灰度值fp大于或等于该灰度值,则将该点设成1,否则为0。对其8邻域进行0/1编码,得到一个长度为8的二进制串,用该二进制串作为该像素的编码,如式(1)
| $ {\rm{LP}}{{\rm{B}}_{\mathit{P, R}}} = \sum\limits_{p = 0}^{P - 1} {s\left( {{f_p} - {f_c}} \right) \cdot {2^p}}, $ | (1) |
其中:
| $ \begin{array}{l} {\rm{LPB}}_{_{\mathit{P, R}}}^{ri} = \left. {\min \{ {\rm{ROR}}\left( {{\rm{LB}}{{\rm{P}}_{\mathit{P, R}}}, \mathit{i}} \right)} \right|\\ \;\;\;\;\;\;\;\;\mathit{i = }{\rm{0}}\mathit{, }{\rm{1}}\mathit{, } \cdots \mathit{, P}{\rm{ - 1}}\} \end{array}。$ | (2) |
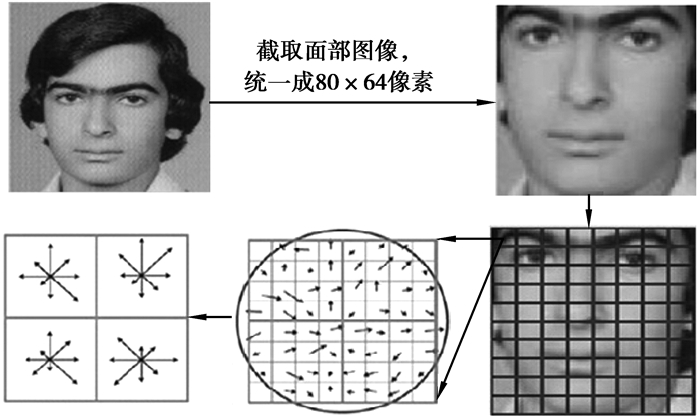
|
图 3 HOG直方图序列提取过程 |
LBP特征用于人脸年龄估计,如图 2所示的网格人脸灰度图,对这80个小区域分别进行LBP特征的提取,并计算每个区域的直方图,最后将所有区域的直方图连接起来作为人脸的表示。Ojala等[13]证明一致模式能表达大部分的纹理信息,并有较好的分类性。采用均匀一致模式LBPP,Rriu2,其中P=8,R=1,u2指的是均匀一致模式,即,不允许二进制编码中0,1的跳变次数超过2次,如式(3)所示,LBPP,Rriu2模式局部区域直方图向量长度为59。
| $ \theta \left( {x, y} \right) = \tan - 1\left. {\left( {I\left( {\mathit{x}, \mathit{y} + 1} \right){\rm{ - }}\mathit{I}\left( {x, y - 1} \right)} \right)/(\mathit{I}\left( {x + 1, y} \right) - I\left( {x - 1, y} \right)} \right), $ | (3) |
| $ m\left( {x, y} \right) = \sqrt {{{\left. {{{\left( {I\left( {\mathit{x}, \mathit{y} + 1} \right){\rm{ - }}\mathit{I}\left( {x, y - 1} \right)} \right)}^2}+(\mathit{I}\left( {x + 1, y} \right) - I\left( {x - 1, y} \right)} \right)}^2}}, $ | (4) |

|
图 2 LBP算子提取过程 |
HOG特征用于人脸年龄估计源于Déniz等[12]人将HOG特征成功用于人脸识别,HOG描述子是Lower的尺度不变特征变换(SIFT)算法的第三步。HOG描述子首先确定一个以关键点为中心的领域作为采样窗口,以8×8的像素领域(block)作为关键点的采样窗口为例。首先将采样窗口均分为4个相等大小的块(以下都称为块或者cell),每个块大小是4×4;再用式(3)、(4)分别计算每个小块上每个像素的梯度方向和梯度幅值,如图 5左部分所示,箭头代表梯度的方向。
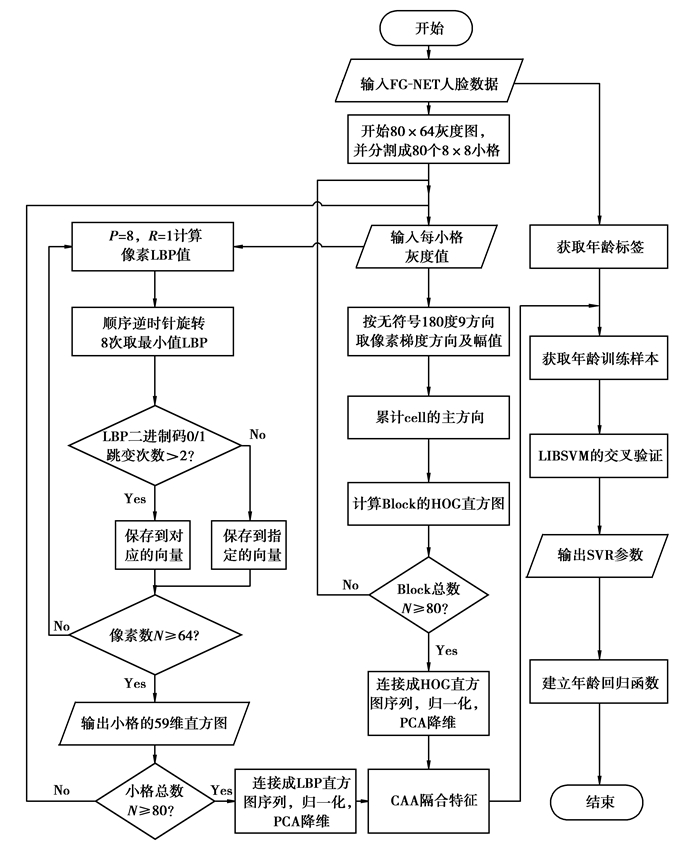
|
图 5 年龄回归函数算法流程图 |
其中I(x,y)为像素点(x,y)上的灰度值,θ(x,y)为像素点(x,y)上的梯度方向,m(x,y)为(x,y)上的梯度幅值。按图 3方法将人脸所有像素作为关键点,梯度方向选择无符号180° 9个方向,每个窗口(4个小格)有36维的直方图向量,整个人脸HOG特征直方图序列长度为80×36。
1.3 年龄变化特征提取研究方法的工作步骤图 4所示及回归函数算法流程如图 5所示。
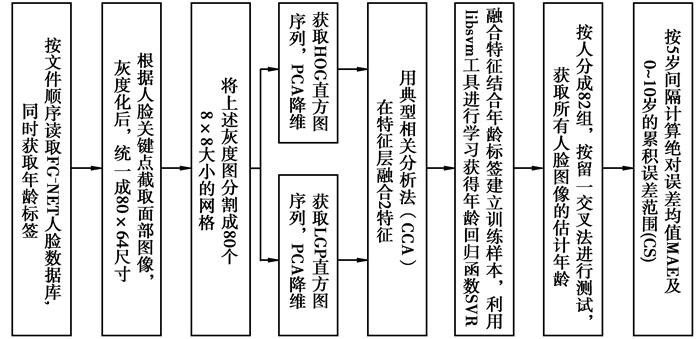
|
图 4 研究方法年龄估计实现流程图 |
典型相关性分析是一种统计两种随机变量之间关系的一种方法。假设向量空间X=[x1,x2,…,xn],xi∈Rm和Y=[y1,y2,…,yn],yi∈Rn分别表示人脸图像的LBP特征和HOG特征。CCA的目的就是找到一对投影轴,wx和wy,使得线性组合α=wxTx和β=wyTx之间的相关度最大,关联系数Corr(α,β)由判别准则如式(5)确定
| $ {\rm{Corr}}\left( {\alpha, \beta } \right) = \mathop {\max }\limits_{{\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{x}}}, {\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{y}}}} \frac{{\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{x}}^{\rm{T}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{xy}}}}{\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{y}}}}}{{\sqrt {\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{x}}^{\rm{T}}\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{xx}}}^{\rm{T}} \cdot {\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{y}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{yy}}}}{\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{y}}}} }}, $ | (5) |
其中:Cxy=E[xT y],X,Y间互协方差矩阵,Cxx=E[xT x],X的协方差矩阵,Cyy=E[yT y],Y的协方差矩阵。通过求解形如式(6)的特征方程,可以轻松获得CCA的这组投影轴。
| $ \left[\begin{array}{l} \;\;0\;\;\;\;\;\;\;\;\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\\ \mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\;\;\;\;\;\;\;0 \end{array} \right]\;\left[\begin{array}{l} {\mathit{\boldsymbol{w}}_x}\\ {\mathit{\boldsymbol{w}}_y} \end{array} \right] = \lambda \left[\begin{array}{l} \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\;\;\;\;0\\ 0\;\;\;\;\;\;\;\;\mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{Y}}^{\rm{T}}} \end{array} \right]\;\left[\begin{array}{l} {\mathit{\boldsymbol{w}}_x}\\ {\mathit{\boldsymbol{w}}_y} \end{array} \right], $ | (6) |
其中λ就是Corr(α,β),α和β的相关系。
2 年龄回归假设T=[t1,t2,…,tN]和L=[l1,l2,…,lN]分别表示人脸年龄变化特征训练集及其对应的年龄标签,其中ti∈Rd,li∈R,i=1,2,…,N,d为人脸年龄变化的特征维数,N为训练集的总数。回归函数
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\mathop {\min }\limits_{w, b, \xi } \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + C\sum\limits_{i = 1}^N {{\xi _i}}, \\ {\rm{s}}.\;\;{\rm{t}}.\;\;{{\boldsymbol{y}}_i}\left[{\left( {\mathit{\boldsymbol{w}} \cdot {\mathit{x}_\mathit{i}}} \right) + b} \right] = 1 - {\xi _i}i = 1, 2, \cdots, N。\end{array} $ | (7) |
而核技巧则是用核函数将输入空间中的样本经过非线性变换映射到高维空间中实现线性分类,且不增加计算复杂度。采用径向基函数作为核函数
| $ K\left( {\mathit{\boldsymbol{x}}, z} \right) - \exp \left( { - {\rm{gmma}}{{\left\| {\mathit{\boldsymbol{x}} - z} \right\|}^2}} \right)。$ | (8) |
其中,gmma=1/2σ2;支持向量机遵循机器学习的一般规律,即选择模型(决策函数集合),确定策略(最优决策函数得准则),利用交叉验证的方法选择式(7)中C惩罚参数及式(8)中gmma数值确定回归函数,age=f(x)。
3 仿真实验结果笔者采用2种较为流行的评估方法,绝对错误均值(MAE)及累计误差尺度(CS)。绝对错误均值指的是年龄估计值和实际年龄间错误绝对值与测试样本数的比值,如公式(9)
| $ {\rm{MAE = }}\sum\limits_{i = 1}^{{N_t}} {\left| {{{\hat A}_i} - {A_i}} \right|} /{N_t}, $ | (9) |
其中
| $ {\rm{CumScore}}\left( \theta \right) = {N_{e \le \theta }}/{N_t} \times 100\% ,$ | (10) |
其中Ne≤θ表示估计年龄绝对误差小于θ的测试样本的总数。
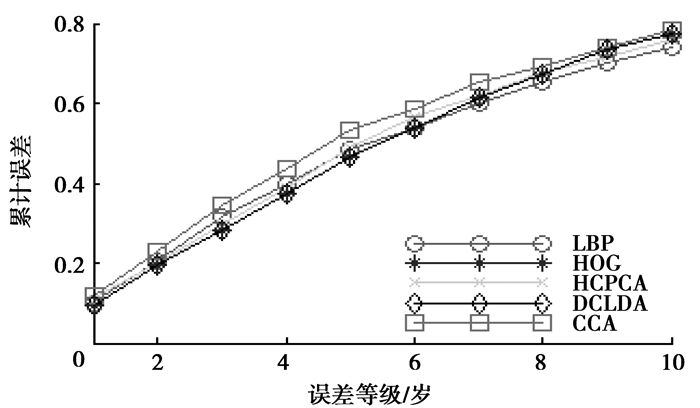
实验所用人脸数据库FG-NET包含82个人的1 002张年龄范围在0~69岁的照片,且照片的光照条件、表情及姿势都有很大的差异研究方法未做灰度均衡,及人脸做矫正的预处理,以验证算法对复杂人脸的有效性。实验对CCA融合的特征,仅HOG特征,仅LBP特征、PCA直接融合(DCPCA)及LDA直接融合(DCLDA)的实验结果作了对比,表 2列出了几种方法在数个年龄段中的MAE值;图 6显示了绝对误差从0~10岁的累计尺度。支持向量机回归SVR的参数选择使用台湾大学林智仁等制作的LIBSVM软件包中的方法,获取不同特征对应的回归模式参数如表 1。
| 表 2 比较选取不同特征年龄估计的均值绝对误差 |
|
图 6 研究方法FG-NET的误差等级从0~10岁的年龄估计的累积误差 |
| 表 1 训练集在交叉留一测试下支持向量机回归参数 |
其中,C表示对误差的宽容度(值越大越不能容忍);Gmma=-1/2σ2, σ2为核函数的方差;P为损失函数参数。
对实验结果的观测可以得出下面3个判断:
1) 对于复杂环境的人脸图像,在不进行灰度均衡、面部矫正等预处理的前提下,采用LBP和HOG特征的人脸分析方法对人脸年龄估计有效。
2) 融合人脸LBP和HOG特征的估计年龄的方法比单独使用LBP特征或单独使用HOG特征方法性能优越,表明多特征融合的比单个特征在人脸年龄估计方面有更好的表现。
3) 相较特征直接融合的方法,典型相关分析(CCA)方法能更好地揭示LBP和HOG信息间的关联关系,因而对人脸年龄估计的效果更好。
4 结论研究方法提取与年龄变化关系紧密的人脸的局部统计特征,LBP特征和HOG特征,并用CCA的方法融合,最后通过SVR的方法对FG-NET人脸库进行训练和测试。该方法的实验中在没有对人脸图像做人脸矫正的情况下也取得良好的效果,FG-NET库中所有的年龄范围的MAE为6.968 0。未来的工作中实现人脸图像面部的自动检测提取,及找到更好的年龄回归的方法,并结合年龄定序的特点[14-15]使年龄估计的方法向实际应用更近一步。当然建立一个更加完备年龄人脸数据库是更为迫切。
| [1] | Kwon Y H, Lobo N D V. Age classification from facial images[J]. Computer Vision and Image Understanding, 1999, 74(1): 1–21. DOI:10.1006/cviu.1997.0549 |
| [2] | Geng X, Zhou Z H, Kate S M. Automatic age estimation basedfacial aging patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(12): 2234–2240. DOI:10.1109/TPAMI.2007.70733 |
| [3] | Geng X, Kate S M. Facial age estimation by multiliner subspace analysis[C]//Proceeding of 2009 IEEE International Conference on Acoustics Speech Signal Processing, April 19-24, 2009, Taipei. Piscataway:IEEE Press, 2009:865-869. |
| [4] | Fu Y, Huang T S. Human age estimation with regression on discriminative aging manifold[J]. IEEE Transactions on Multimedia, 2008, 10(4): 578–584. DOI:10.1109/TMM.2008.921847 |
| [5] | Lu J W, Tan Y P. Ordinary preserving manifold analysis for human age and head pose estimation[J]. IEEE Transactions on Human-Machine Systems, 2013, 43(2): 249–258. DOI:10.1109/TSMCC.2012.2192727 |
| [6] | Yan S C, Wang H, Tang X O, et al. Regression from uncertain labels and its applications to soft biometrics[J]. IEEE Transactions on Information Forensics and Security, 2008, 3(4): 698–708. DOI:10.1109/TIFS.2008.2006585 |
| [7] | Yan S C, Liu M, Huang T S. Extracting age information from local spatially flexible patches[C]//Proceedings of 2008 IEEE International Conference on Acoustics, Speech, and Signal Processing, March 31-April 4, 2008, Las Vegas, NV. Piscataway:IEEE Press, 2008:737-740. |
| [8] | Lu J W, Tan Y P. Fusing shape and texture information for facial age estimation[C]//Proceedings of 2011 IEEE International Conference on Acoustics, Speech, and Signal Processing, May 22-27, 2011, Prague. Piscataway:IEEE Press, 2011:1477-1480. |
| [9] | Dibeklioglu H, Salah A A, Gevers T. A statistical method for 2-D facial landmarking[J]. IEEE Transactions on Image Processing, 2012, 21(2): 844–858. DOI:10.1109/TIP.2011.2163162 |
| [10] | Hardoon D R, Szedmak S, John S T. Canonical correlation analysis:An overview with application to learning methods[J]. Neural Computation, 2004, 16(12): 2639–2664. DOI:10.1162/0899766042321814 |
| [11] | Daugman J. Face and gesture recognition:overview[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 19(7): 675–676. |
| [12] | Déniz O, Bueno G, Salido J, et al. Face recognition using histograms of oriented gradients[J]. Pattern Recognition Letters, 2011, 32(12): 1598–1603. DOI:10.1016/j.patrec.2011.01.004 |
| [13] | Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary pattern[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971–987. DOI:10.1109/TPAMI.2002.1017623 |
| [14] | Lu J W, Tan Y P. Ordinary preserving manifold analysis for human age and head pose estimation[J]. IEEE Transactions on Human-Machine Systems, 2013, 43(2): 249–258. DOI:10.1109/TSMCC.2012.2192727 |
| [15] | Chao W L, Liu J Z, Ding J J. Facial age estimation based on label-sensitive learning and age-oriented regression[J]. Pattern Recognition, 2013, 46(3): 628–644. DOI:10.1016/j.patcog.2012.09.011 |
 2014, Vol. 37
2014, Vol. 37

