2. 空间电子信息技术研究院, 西安 710000
2. Academy of Space Electronic Information Technology, Xi'an, 710000, China
BOC(binary offset carrier)调制技术在新一代卫星导航系统中得到广泛应用[1-2],Galileo卫星导航系统的10种导航信号中有8种使用了BOC调制或改进BOC调制[3-4],中国正在研制的新一代导航卫星系统中,导航信号中也将采用BOC调制技术[5-6]。BOC技术的应用实现了不同程度的信号频谱分离,避免导航信号与其他信号频谱重叠,降低了信号间的相互干扰,改善了系统定位性能、提高了系统抗干扰和抗多径能力[7-8]。
卫星导航系统用户的定位通过测量星地伪距来实现,必须对卫星导航信号发射通道本身的时延进行校准,才能得到实际的星地距离。导航卫星下行发射通道零值的精密测量是卫星导航系统实现精确定位应用的前提之一,零值测量精度将直接影响用户的定位精度。
文献[9]提出一种时延测试方法,对被测件测量相频曲线后计算泰勒系数,根据泰勒系数求被测件时延,这种方法仅适合输入输出频率不发生变化的器件。文献[10]中给出一种称为双频相差法的测试方法,利用双频单边带调制信号作为测试信号,精确测量2个频率间的相位差来得到被测件时延。文献[11]给出了一种采用梳状信号发生器作为基带信号对载波调制形成被测件输入信号,对被测件输出信号解调并与参考本振信号比相,实现频率变换器件的时延测试。由于导航卫星的BOC导航信号发射通道完成从数字基带、扩频、副载波调制及载波调制变频等过程,不是一个简单的信号放大或信号变频变换过程,所以文献[9-11]方法不能对这种数字信号处理通道进行时延测试。
频带受限的数字相位键控调制信号在相邻码元的相位转换点附近会产生幅度的平滑陷落,因此,文献[12-14]中分别针对不同的待测数字调制信号时延提出了示波器观察法,观察示波器显示波形,测量基准参考脉冲的上升沿与待测信号传输通道输出的数字键控载波调制包络波形陷点之间的时延,从而得到待测信号传输通道零值。示波器观察法的局限性是:1)被测件的通道零值不能超过一个数字调制码元时延宽度,否则将出现整码元时延的模糊,从而引起大的测量误差;2)示波器观察陷波点误差大,误差为数ns量级;3)不适合同一频点存在多种调制信号混合输出的情况。
为了解决目前方法不适合BOC调制信号通道高精密零值测试问题,提出一种采用数字域部分相关处理的零值测试方法,对BOC采样数据进行本地相关捕获处理,处理的数据长度小于一个BOC信号的伪随机码周期。提出方法测试结果精度高,而且解决了示波器码元整周模糊问题。
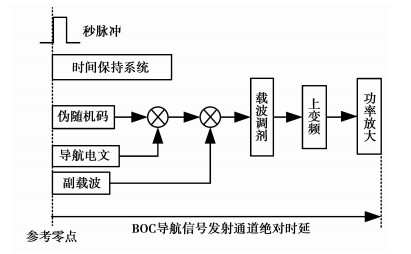
1 BOC信号发射通道零值定义卫星导航信号发射通道组成如图 1所示,由导航信号随机码发生、导航电文生成、副载波生成、载波调制、上变频和功率放大器组成。定义BOC导航信号发射通道绝对时延的起始零点为导航卫星时间保持系统生成的秒脉冲信号(1PPS)的上升沿,BOC导航信号发射通道的绝对时延定义为与秒脉冲信号上升沿对齐的伪随机码片经过发射通道后与该秒脉冲信号上升沿之间的时延差。
|
图 1 BOC信号通道组成框图 |
提出的零值测试方法实现原理如图 2所示。

|
图 2 零值测试原理 |
使用1PPS脉冲的上升沿触发A/D转换器进行采样,高速A/D转换器1和2对导航卫星输出的BOC信号和1PPS脉冲进行同步采样,采样频率高于BOC信号最高频谱的2倍以上。通过高采样频率来保证测试的高精度。
传统的扩频信号捕获方法使用一个伪随机周期的信号进行相关捕获,高采样率导致BOC信号样本数据量巨大,传统方法实现困难。本算法中采用部分相关捕获方式,即就是使用伪随机码周期内的某一段进行相关处理,捕获计算量与参与捕获处理的伪随机码片个数的平方成正比,采用部分相关捕获方式,大大降低了单次捕获处理中计算量,使得捕获处理得以实现。
以GPS卫星C/A码作为分析对象。从一个伪随机码周期内的起始码片开始截取一段伪随机码,计算GPS卫星32个C/A码截取码的自相关和互相关电平情况。
| $ {R_{CC}} = \max \left( {\left| {\sum\limits_{l = 0}^N {{C^i}\left( l \right){C^k}\left( {l + m} \right)} } \right|} \right), i \ne k, $ | (1) |
其中:N为PRN码周期起始码开始截取码片长度;m=1,2,…,N;Ci为卫星i的PRN码;Ck为卫星k的PRN码;Rcc为码组内任意2个伪随机码互相关峰值的最大值。
在零多普勒频差的条件下,C/A码的自相关函数电平与最大互相关函数峰值电平差。
| $ {\Delta _{PP}} = 20\log \left( {\frac{N}{{{R_{cc}}}}} \right)。$ | (2) |
不同截取长度情况,C/A的自相关电平和互相关电平差如表 1所示。随着截取码的长度增大,电平差为增大趋势,N取50时,ΔPP为5.03 dB,N为1 023时,ΔPP为23.94 dB。
| 表 1 截取伪随机码的相关特性结果 |
在卫星的导航信号通道时延零值测试过程中,仅对一个频点导航信号进行有线状态的采样数据进行处理,不存在导航信号的远近效应或多径效应现象,只需要保证ΔPP能足以完成正确的捕获就可以了,选择5 dB作为判决门限,可以确保没有干扰的有线连接状态下C/A信号的正确捕获,所以截取码片长度大于50就可以满足要求。
部分相关捕获中截取的C/A信号样本点数L为
| $ L \geqslant \frac{{{C_L}}}{{1023}}{f_s} \times {10^{ - 3}}, $ | (3) |
其中:CL为截取的伪随机码段中包含的码片个数;fS为采样频率。
为了实现快速傅立叶变换处理,要求L=2M,M为一个正整数。
本地C/A伪随机码发生器以采样率fS生成一个周期的伪随机码样本值,码型与待测试卫星信号的码型一致,然后,截取起始的L个样本点
| $ \mathit{\boldsymbol{D}}_C = \left[{{d_C}\left( 1 \right)\;\;{d_C}\left( 2 \right)\;\; \cdots {d_C}\left( L \right)} \right]。$ | (4) |
副载波生成器以采样率fS生成一个周期的副载波样本值,截取起始的L个样本点
| $ \mathit{\boldsymbol{D}}_S = \left[{{d_S}\left( 1 \right)\;\;{d_S}\left( 2 \right)\;\; \cdots {d_S}\left( L \right)} \right]。$ | (5) |
伪随机码样本与副载波样本值进行模2加处理,形成本地基带数据样本
| $ \mathit{\boldsymbol{D}}_B = \left[{{d_B}\left( 1 \right)\;\;{d_B}\left( 2 \right)\;\; \cdots {d_B}\left( L \right)} \right], $ | (6) |
其中dB(k)=dC(k)⊕dS(k)k=1,2,…,L⊕2加处理。
设置本地载波频率为
| $ {{f}_{0}}={{f}_{c}}+\left( l-n \right)\centerdot {{f}_{t}}, $ | (7) |
其中:fc本地载波频率的中心频率;ft为频率变化的步进量;±n·ft以fc为中心频率的变化范围;l=1,2,…,2n+1。
本地载波各频点后对L个本地C/A伪随机码数据进行载波正交调制。
| $ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{D}}}_{L}}= \\ &\left[ \begin{matrix} {{d}_{L}}\left( 1,1 \right) & {{d}_{L}}\left( 1,2 \right) & \cdots & {{d}_{L}}\left( 1,L \right) \\ {{d}_{L}}\left( 2,1 \right) & {{d}_{L}}\left( 2,2 \right) & \cdots & {{d}_{L}}\left( 2,L \right) \\ \cdots & \cdots & \ddots & \vdots \\ {{d}_{L}}\left( 2n+1,1 \right) & {{d}_{L}}\left( 2n+1,2 \right) & \cdots & {{d}_{L}}\left( 2n+1,L \right) \\ \end{matrix} \right], \end{align} $ | (8) |
其中,dL(l,m)=dC(m)
对1PPS脉冲采样数据进行处理,脉冲上升沿变化点就确定为BOC通道时延的起始点,其样本点序号用S表示。
根据通道零值的起始点序号S以及规定的截取长度L,从采集的BOC信号数据中,从第S+1个样本点开始读取L个样本点,然后进行希尔伯特变换,得到一个长度为L的复数数据组作为通道零值测试的待处理BOC信号数据
| $ {{\mathit{\boldsymbol{D}}}_{s}}=\left[{{d}_{s}}\left( 1 \right)\ \ {{d}_{s}}\left( 2 \right)\ \ \cdots {{d}_{s}}\left( L \right) \right]。$ | (9) |
L点待处理BOC信号数据经过FFT(fast fourier transform快速傅立叶变换)后取共扼,得到L点频域值
| $ \begin{align} &\mathit{\boldsymbol{X}}\left( m \right)={{\left[\sum\limits_{k=1}^{L}{{{d}_{c}}\left( k \right)\exp \left(-j\frac{2\pi m}{L}\left( k-1 \right) \right)} \right]}^{*}}, \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ m=1, 2, \cdots L。\\ \end{align} $ | (10) |
本地参考数据数组各行分别进行FFT,得到一个2n+1行L列的频域值数组
| $ \begin{align} &Y\left( l, m \right)=\left[\sum\limits_{k=1}^{L}{{{d}_{L}}\left( l, k \right)\exp \left(-j\frac{2\pi m}{L}\left( k-1 \right) \right)} \right], \\ &\ \ \ l=1, 2, \cdots, 2n+1, m=1, 2, \cdots L。\\ \end{align} $ | (11) |
(2n+1)×L的频域值数组的每一行,分别与BOC信号的频域共轭数据相乘,再经过IFFT(inverse fast fourier transform逆傅立叶变换),得到一个2n+1行L列时域相关值数组
| $ \begin{align} &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Z\left( l, m \right)= \\ &\sum\limits_{k=1}^{N}{\left[x\left( k \right)\centerdot Y\left( l, k \right)\exp \left(-j\frac{2\pi m}{L}\left( k-1 \right) \right) \right]} \\ \end{align}。$ | (12) |
对(2n+1)×L的时域相关值数组各复数值求幅度值,然后取平方
| $ {{Z}_{P}}\left( l, m \right)={{\left| Z\left( l, m \right) \right|}^{2}}。$ | (13) |
对2n+1组时域幅度平方数据进行峰值搜索,峰值点所在行的列序号NBOC就是BOC信号中的伪随机码的起始点。将BOC伪随机码的起始点序号乘以采样间隔,加上1PPS到A/D转换器2的信号传输时延,减去卫星BOC信号输出到AD转换发器1之间的信号传输时延,就得到了BOC信号通道零值tL1。
| $ {{t}_{L1}}={{N}_{\rm{BOC}}}\centerdot \frac{1}{{{f}_{S}}}+{{t}_{Z}}-{{t}_{\rm{out}}}, $ | (14) |
其中:tZ为1PPS脉冲信号到A/D转换发器2的信号传输时延;tout为导航卫星BOC信号输出到A/D转换发器1之间的信号传输时延。
对时延测试算法实现过程中可能产生的误差因素进行分析
1) 高速A/D采样电路参考时钟的准确度。由于在采样数据的时延测试处理中,伪随机码起始点序号与秒脉冲上升沿采样点序号进行差分处理,从而消除了A/D采样电路参考时钟的准确度误差,误差仅取决于参考时钟的短期稳定度,高稳晶体振荡器产生参考时钟,其秒稳定度可达1e-10,最大误差为:一个码片的周期×2×1e-10。BOC信号伪码速率为1.023 MHz,则A/D采样电路参考时钟稳定度造成的测量最大误差为1.95e-7 ns,可忽略。
2) 基于延迟锁定环路的扩频相关技术在白噪声情况下,引起时延误差的不确定度为[15]
| $ {{\sigma }_{t}}={{T}_{c}}\sqrt{\frac{d}{4TC/{{N}_{0}}}}, $ | (15) |
其中:σt为测试的时间误差的标准差;Tc为码片的宽度,1/1 023 ms;T为运算的平均时间,这里为CL/1 023 ms;d为相关过程的移动码宽,这里为1/fS;C/N0为信号的载噪比,这里可用取典型值46.5 dBHz。
截取码片个数CL为50时,CL/1 023约为48.9 μs时,σt为0.07 ns。
3) 测试系统连接电缆时延校准误差。采用矢量网络分析器校正电缆时延,校正结果误差不确定度小于0.1 ns。
4) 高速A/D采样电路时间分辨率误差。采样频率为10 GSa/s,每个采样周期为0.1 s,因此时间分辨率误差为0.1 ns。
5) 考虑到环境温度和测试系统设备的转接头的影响因素,导致测量误差不确定度小于0.1 ns。
综合上述各项误差分析,采用本文提出的测试算法进行C/A信号发射通道的时延测试,测试结果的不确定度小于
用软件模拟产生Galileo卫星L1导航信号[16],采用BOC(1,1)方式,伪随机码和副载波频率均为1.023 MHz,载波中心频率为1 575.42 MHz。测试仿真验证参数为:A/D采样率为10 Gsa/s、时延测试分辨率为0.1 ns。生成具有设定时延的导航信号后,利用提出的算法,对数据进行处理,得到导航信号的时延量,与设定的时延量比较,从而验证提出方法的正确性。
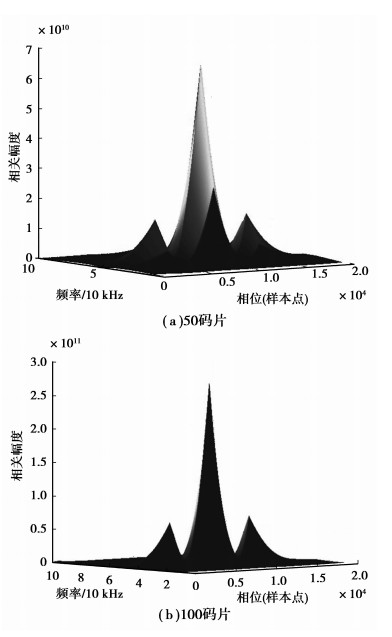
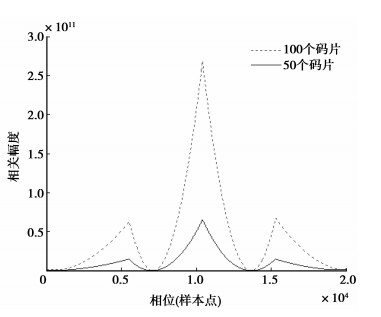
通道时延设定为1 042.1 ns,相当10 421个样本点。截取的BOC信号长度等于50个伪随机码片时,对信号的频率相位相关捕获结果如图 3(a)所示。截取的BOC信号长度等于100个伪随机码片时,对信号的频率相位相关捕获结果如图 3(b)所示。2种情况,得到延时量均为10 421个样本点。在多普勒频率为0时,2种情况的相关曲线如图 4所示,从图上看到截取码片个数多,参加处理的样本点个数多,相关峰值越高,但是不能改变峰值点对应的样本数据序号,对测量精度没有本质的影响。
|
图 3 2种情况的BOC(1,1)信号捕获 |
|
图 4 2种情况的相关曲线 |
分别采用提出方法和示波器观察法对BOC信号发射通道的零值进行测量,并对测试结果进行比较。BOC信号发射通道输出信号与导航信号生成系统的1PPS脉冲输出分别接入到高速数字示波器的2个输入通道,示波器型号为Agilent公司的DSO90804A,用1PPS脉冲的上升沿触发高速示波器的双通道采样。
提出测试方法的具体实现为:控制计算机经网络接口控制高速示波器,对2个输入同步采样,根据提出测试方法编写数据处理软件,利用软件完成零值测试。
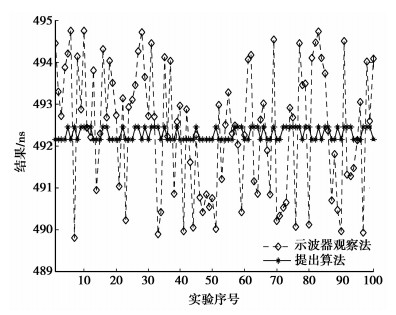
采用提出方法和示波器观察法各进行100次的时延测试,测试结果如图所示。采用示波器观察法得到的时延值的不确定度为1.39 ns,采样提出算法的测试的时延值不确定度为0.14 ns。
|
图 5 图测试结果 |
根据分析和试验系统的测试结果,可以得到如下结论:
1) 采用提出的测试方法,解决了示波器观察法只能得到低于一个基带码片的时延量而无法获取完整的时延值问题,可以得到发射通道的完整时延零值;
2) 测试结果获取依靠数字处理,算法减少硬件资源的占用,而且采用数字域处理方式,每个采样点的序号是可以明确的,处理过程带来时延能进行精确的校准,这样信号的处理过程中不会引入时延测量误差;
3) 截取BOC导航信号样本点进行捕获处理,这种不完全伪随机码周期的相关方式,对测量精度影响可以忽略,可以显著地降低了捕获运算中运算量,保证了高采样率的数据处理得以实现;
4) 由于采用相关处理,不需要考虑信号波形,所以提出测试方法可以用于同一频点多种调制信号存在的情况。
| [1] | Emmanuele A. Spread-spectrum continuous-phase-modulated signals for satellite navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3234–3249. DOI:10.1109/TAES.2012.6324699 |
| [2] | Liu W, Hu Y, Zhan X Q. Generalised binary offset carrier modulations for global navigation satellite systems[J]. Electronics Letters, 2012, 48(5): 284–286. DOI:10.1049/el.2011.3278 |
| [3] | Martinez-belda M C. On the potential of galileo E5 for time transfe[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2013, 60(1): 121–131. DOI:10.1109/TUFFC.2013.2544 |
| [4] | Wullems C J. A spoofing detection method for civilian L1 GPS and the E1-B Galileo safety of life service[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 2849–2864. DOI:10.1109/TAES.2012.6324665 |
| [5] | Tang Z P, Zhou H W, Wei J L, et al. TD-AltBOC:A new COMPASS B2 modulation[J]. Science China:Physics, Mechanics & Astronomy, 2011, 54(6): 1014–1021. |
| [6] | Gao G X, Enge P. How many GNSS satellites are too many[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 2865–2874. DOI:10.1109/TAES.2012.6324666 |
| [7] | Zhou Y L, Hu X L, Ke T, et al. Ambiguity mitigating technique for cosine-phased binary offset carrier signal[J]. IEEE Transactions on Wireless Communications, 2012, 11(6): 1981–1984. DOI:10.1109/TWC.2012.041612.110531 |
| [8] | Juang J C, Kao T L. Noncoherent BOC signal tracking based on a five-correlator architecture[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 1961–1974. DOI:10.1109/TAES.2012.6237573 |
| [9] | Zhu X W, Li Y L, Yong S W, et al. A novel definition and measurement method of group delay and its application[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(1): 229–233. DOI:10.1109/TIM.2008.927197 |
| [10] | Yu C J, Lin J. Method and its optimization for group delay measurement of Frequency-Translating Devices by using double-frequency phase difference method[C]//Proceedings of the 10th International Conference on Electronic Measurement & Instruments, August 16-19, 2011, Chengdu, China. Piscataway:IEEE Press, 2011, 4:63-67. |
| [11] | Scott J, Hoy M. Group-Delay measurement of frequency-converting devices using a comb generator[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(11): 3012–3017. DOI:10.1109/TIM.2010.2045972 |
| [12] | Plumb J, Larson K M, White J, et al. Absolute calibration of a geodetic time transfer system[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2005, 52(11): 1904–1911. DOI:10.1109/TUFFC.2005.1561658 |
| [13] | Xu L J, Li X M. Dual-channel pseudorandom sequence generator with precise time delay between its two channels[J]. IEEE transactions on Instrumentation and Measurement, 2008, 57(12): 2880–2884. DOI:10.1109/TIM.2008.926427 |
| [14] | Rashidzadeh R, Ahmadi M, Miller W C. An all-digital self-calibration method for a Vernier-based time-to-digital converter[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(2): 463–469. DOI:10.1109/TIM.2009.2024699 |
| [15] | Misra P, Enge P. Global positioning system signal, measurement, and performance[M]. Ganga: Jamuna Press, 2006. |
| [16] | Gianni D, Lisi M, De S P, et al.A model-based signal-in-space interface specification to support the design of Galileo receivers[C]//Proceedings of the 6th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, ,December 5-7, 2012, Noordwijk, Netherlands. Piscataway:IEEE Press, 2012:1-8. |
 2014, Vol. 37
2014, Vol. 37


