摆动液压缸的工作原理是输入液压力沿轴向推动油缸活塞,通过活塞和缸体之间的螺旋副,直线运动则变成了旋转运动,由于螺旋副间隙间存在液压油,因此这样的传动结构有很高的效率,能够在非常小的结构尺寸下输出较大的扭矩,而且螺旋副传动的结构本质非常简单,所以也很好维护,该产品广泛应用于工业各个领域中,尤其适用于大扭矩、短力臂的工况。目前这种类型的产品专利和相应的生产技术被国外公司所垄断,而且他们通过与大学进行技术合作,产品的可靠性都有非常好的保证。国内对此类产品的研究还非常的少。
虚拟样机技术(virtual prototype technology)是一种近年来新起的产品开发技术。得益于计算机技术的迅猛发展,产品开发团队在计算机上设计出产品的三维CAD模型,进行虚拟装配过程,以检查产品零部件装配工艺性和干涉情况,对产品进行多体动力学仿真(MBD)和有限元分析(FEM),以检查零部件物理性能。由于虚拟样机在物理特性上非常接近物理样机,可以帮助企业缩短产品开发周期,降低生产成本,提高产品质量[1-4]。这项由国外大型企业应用需求而产生的技术现在在国内也逐步开始应用。
通过NX 7.5设计好摆动液压缸的产品虚拟样机,对摆动液压缸的双级渐开线螺旋副[5]进行研究:螺旋副的螺旋角一致的工况下,输入液压力P与输出扭矩T的关系;输入液压力P一致的工况下,螺旋角β和输出扭矩T的关系。运用虚拟的摆动液压缸进行各种仿真研究,可以有效提升实验效率,并大幅降低实验成本,仿真结果对摆动液压缸的优化设计具有非常明显的效果[6]。
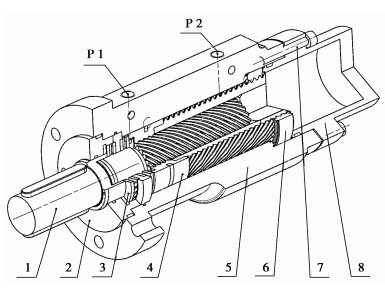
1 摆动液压缸工作原理文中研究了输出回转角度为360°的摆动液压缸,主要由前部端盖、输出右旋外齿轮、止推滚针轴承、油缸缸体、活塞齿轮、左旋内齿轮、后部端盖和内六角螺栓组成。其中活塞齿轮是由一个左旋外空心齿轮和一个右旋内齿轮刚性联结而成,其左旋外空心齿轮与左旋内齿轮组成一组渐开线螺旋副。其右旋内齿轮与输出右旋外齿轮组成另一组渐开线螺旋副,因为渐开线键具备齿形定心能力,特别适合传递大扭矩,因而这两组渐开线螺旋副组成了摆动液压缸核心构件。360°摆动液压缸的结构见图 1所示。
|
图 1 360°摆动液压缸结构图 注:1.输出右旋外齿轮;2.前部端盖;3.止推滚针轴承;4.活塞齿轮;5.油缸缸体;6.左旋内齿轮;7.内六角螺栓;8.后部端盖 |
在油缸缸体内部,活塞齿轮和其外部装配的密封环将缸体内部腔室分割开来,沿油缸轴向形成左右2个独立的腔室,2个腔室分别与油口P1、P2相通。当右侧腔室的压力大于左侧腔室压力的时候,活塞齿轮在液压力的推动下自右向左运动,由于活塞齿轮与左旋内齿轮组成的左旋螺纹副作用,活塞齿轮还产生顺时针的旋转运动(自左向右看)。活塞齿轮又与输出右旋外齿轮组成一对右旋螺旋副,该螺旋副使输出右旋外齿轮也产生顺时针旋转运动(自左向右看),通过双级螺旋副的旋转叠加作用,只要很小的直线工作行程,就能输出相当可观的工作旋转角度,因此,摆动液压缸可以设计得非常紧凑。反之,当油缸右侧腔室的压力小于左侧腔室的压力时,输出右旋外齿轮将得到反方向的输出旋转。由于液压力在左右两侧腔室有同样大小的作用投影面积,因此,当两侧腔室的液压力压差是同样的情况下,摆动液压缸输出的正反转扭矩大小也完全一样[7]。
活塞齿轮通过液压力的作用,其做直线并旋转运动,双螺旋副上将产生很大的径向分力、轴向分力和周向分力。径向分力和轴向分力转变成为了系统的内力,而周向分力则形成输出扭矩,由此可知,周向分力和输出扭矩是线性正比的关系。
当输出右旋外齿轮上的键与机械设备联结好以后,油缸缸体上的联结法兰可能与机械设备上的法兰存在角度偏差,这时,可以松开后部端盖与油缸缸体的联结螺栓,并拉出后部端盖少许,逆时针调整(自左向右看)油缸缸体,可以使缸体的联结法兰与机械设备上的法兰角度一致,该设计能确保摆动液压缸能够方便准确地安装。
2 虚拟样机的建立 2.1 建模及虚拟装配通过NX 7.5 Modeling建立摆动液压缸各个部件的Part[8-9],将所有渐开线齿轮的螺旋角设为可变参数,便于后期调整[10-11]。先预设螺旋角为45°,不考虑齿轮变位,输出右旋齿轮轴齿顶圆直径da1=32.5 mm,法向模数mn1=1 mm,法向压力角αn1=20°,得齿数z1=22,螺旋角β1=43° 50′14″,右旋;活塞齿轮轴外齿轮齿顶圆直径da2=49 mm,法向模数mn2=1 mm,法向压力角αn2=20°, 得齿数z2=35,螺旋角β2=41° 52′06″,左旋。输入各Part的材料特性。通过计算机进行虚拟的装配,可以检查零部件的干涉情况和装配工艺性的好坏,见图 2所示。

|
图 2 零、部件干涉情况检查和装配工艺性优劣检查 |
通过上述的2项检查,将产品的装配工艺逐步优化,调整产品各零部件的尺寸,使零部件之间无动、静干涉,使摆动液压缸达到预期的尺寸设计要求。
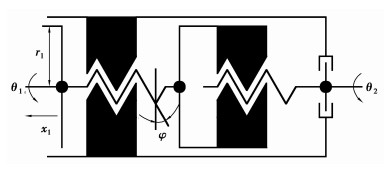
2.2 多体动力学分析(MBD)因为摆动液压缸的运动是在双级渐开线螺旋副之间展开,所以可以简化模型,仅对摆动液压缸的双级螺旋副进行研究,见图 3所示。
|
图 3 双级螺旋副机构简图 |
考虑到各螺旋副之间存在阻尼的影响,因此对研究的系统采用耗散函数的拉格朗日方程[12-16],其表达式为
| $ \frac{\text{d}}{\text{d}t}\left( \frac{\partial E}{\overset{\centerdot }{\mathop{\partial {{q}_{j}}}}\, } \right)-\frac{\partial E}{\partial {{q}_{j}}}+\frac{\partial U}{\partial {{q}_{j}}}+\frac{\partial D}{\overset{\centerdot }{\mathop{\partial {{q}_{j}}}}\, }={{F}_{j}}, $ | (1) |
式中:qj为系统定义的广义坐标系;E为系统具有的动能;U为系统具有的势能;D为系统损失的耗散能;Fj为系统受到的广义外力。
活塞齿轮的周向旋转角度与活塞齿轮的轴向位移关系式为
| $ {{\theta }_{1}}=\frac{\pi }{{{r}_{1}}\centerdot \tan {{\varphi }_{1}}}\centerdot {{x}_{1}}, $ | (2) |
式中:θ1为活塞齿轮周向旋转角度;r1为活塞齿轮左旋外齿轮分度圆半径;φ1为活塞齿轮左旋外齿轮分度圆处螺旋升角, 90°-β1;x1为活塞齿轮轴向位移。
输出右旋外齿轮的周向旋转角度与活塞齿轮的周向旋转角度的关系式为
| $ {{\theta }_{2}}=k{{\theta }_{1}}=\frac{k\centerdot\pi }{{{r}_{1}}\centerdot \tan {{\varphi }_{1}}}\centerdot {{x}_{1}}, $ | (3) |
式中:θ2为输出右旋外齿轮周向旋转角度;k为双级螺旋副放大系数。
系统的动能为
| $ \begin{align} & \ \ \ \ \ \ \ \ E=\frac{1}{2}{{m}_{1}}\overset{\centerdot }{\mathop{x_{1}^{2}}}\,+\frac{1}{2}{{J}_{1}}\overset{\centerdot }{\mathop{\theta _{1}^{2}}}\,+\frac{1}{2}{{J}_{2}}\overset{\centerdot }{\mathop{\theta _{2}^{2}}}\,= \\ & \frac{1}{2}{{m}_{1}}\overset{\centerdot }{\mathop{x_{1}^{2}}}\,+\frac{1}{2r_{1}^{2}{{\tan }^{2}}{{\varphi }_{1}}}{{J}_{1}}\overset{\centerdot }{\mathop{x_{1}^{2}}}\,+\frac{{{k}^{2}}}{2r_{1}^{2}{{\tan }^{2}}{{\varphi }_{1}}}{{J}_{2}}\overset{\centerdot }{\mathop{x_{1}^{2}}}\,, \\ \end{align} $ | (4) |
式中:m1为活塞齿轮的质量;J1为活塞齿轮的转动惯量;J2为输出右旋外齿轮的转动惯量。
系统的势能为
| $ U={{m}_{1}}g{{h}_{1}}+{{m}_{2}}g{{h}_{2}}, $ | (5) |
式中:h1为活塞齿轮质心与水平面距离;m2为输出右旋外齿轮的质量;h2为输出右旋外齿轮质心与水平面距离。
系统耗散能为
| $ \begin{align} &\ \ \ \ \ \ \ \ \ \ \ \ \ \ D=\frac{1}{2}{{c}_{1}}v_{1}^{2}+\frac{1}{2}{{c}_{2}}v_{2}^{2}= \\ &\frac{1}{2}{{c}_{1}}\left( \overset{\centerdot }{\mathop{x_{1}^{2}}}\, +\frac{1}{{{\tan }^{2}}{{\varphi }_{1}}}\overset{\centerdot }{\mathop{x_{1}^{2}}}\, \right)+\frac{1}{2}{{c}_{2}}\left( \overset{\centerdot }{\mathop{x_{1}^{2}}}\, +\frac{{{k}^{2}}}{{{\tan }^{2}}{{\varphi }_{1}}}\overset{\centerdot }{\mathop{x_{1}^{2}}}\, \right), \\ \end{align} $ | (6) |
式中:c1为左旋螺旋副阻尼系数;v1左旋螺旋副间相对线速度;c2为右旋螺旋副阻尼系数;v2为右旋螺旋副间相对线速度。
2.3 仿真计算及结果进入Motion Simulation模块,选用RecurDyn求解器[17-18],定义连杆和运动副。双极螺旋副之间相对速度较小,而且运动副之间还存在液压油,可以将其定义为边界摩擦[19],接着定义螺旋副间的接触参数[20-22]。
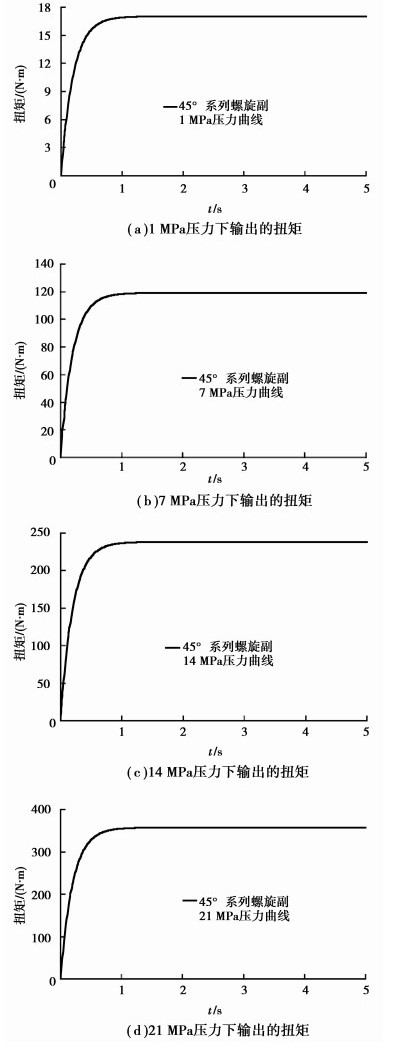
活塞齿轮轴直径为φ50 mm,在轴上对其分别施加1、7、14、21 MPa的输入液压力,取仿真时间为5 s,仿真帧数为500,输出端的扭矩见图 4所示。
|
图 4 不同液压力下的输出扭矩 |
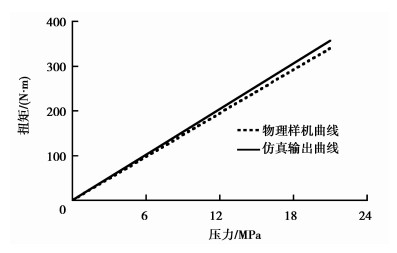
选取系统达到平衡时的扭矩值,通过作图分析(见图 5),可以得出输入液压力与输出扭矩为线性正比关系,物理样机理论输出曲线与仿真输出曲线相比,斜率略低,这是因为简化的模型,忽略了其余零部件的能量损耗[23-24]。
|
图 5 物理样机理论输出曲线与仿真输出曲线对比图 |
根据输入液压力与输出扭矩成线性正比的关系,取定1 MPa定值。改变螺旋齿轮的螺旋角β,研究齿轮螺旋角β与输出扭矩T的关系,另外设计2种螺旋角的螺旋齿轮,分别初定为30°和60°,每个齿轮齿顶圆直径不能改变,定义法向模数mn=1 mm,法向压力角取标准值,αn=20°,暂不考虑齿轮任何变位,另外2组齿轮参数如表 1所示。
| 表 1 30°和60°斜齿轮系列参数 |
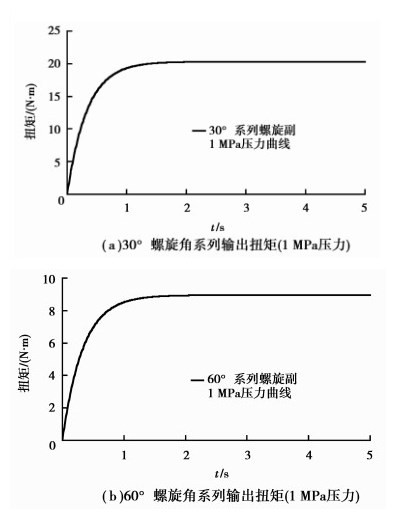
根据前面的仿真步骤对30°和60° 2组渐开线螺旋副仿真,得到的扭矩如图 6所示。
|
图 6 在一样的液压力下,齿轮螺旋角与输出扭矩的关系 |
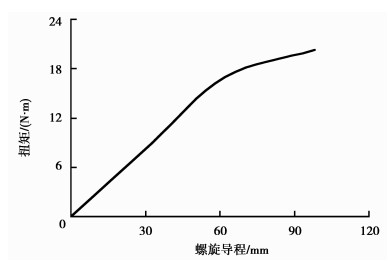
通过图 6,选取系统达到平衡时的扭矩值,在系统液压力为1 MPa的时候,30°系列、60°系列的螺旋副输出扭矩分别是20.32、8.96 N·m,而30°系类、45°系列和60°系列的螺旋导程l分别为98.2、62.2、32.7 mm,由此可以得到输出扭矩和螺旋导程的关系,见图 7所示。
|
图 7 输出扭矩螺旋与导程曲线图 |
导程0~60 mm区间范围内,曲线呈下凹势,说明增大斜齿轮螺旋角的时候,可以有效减少螺旋副的导程,但此时螺旋齿轮的轴向分力增大,螺旋副上摩擦力将迅速增大,此时传动效率呈降低趋势;导程60 mm以后,曲线呈上凸势,说明螺旋齿轮的周向分力增大,同样螺旋副上的摩擦力也迅速增大,同样也降低了螺旋传动的效率。
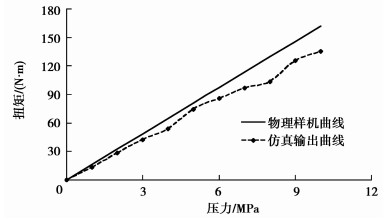
3 实验通过对输出右旋齿轮轴设置扭矩传感器,对摆动液压缸的活塞齿轮轴逐步施加液压力,测试系统压力与输出扭矩的关系,本次实验液压系统最高压力为10 MPa。实验设备与曲线对比见图 8、图 9所示。

|
图 8 实验设备图 |
|
图 9 实验测试曲线与物理样机曲线对比图 |
由于压力表的误差、液压系统的泄漏和液压系统各元器件的不稳定,因而实验测试点存在一定的跳跃性,从图 9可以得出,摆动液压缸实际输出扭矩略低于其理论输出扭矩,但仍可以得到系统液压力与输出扭矩成线性正比关系,仿真结论同样与其吻合。
4 结论通过运用虚拟样机的虚拟仿真和物理样机的实际实验,可以得出输入液压力P和输出扭矩T成线性正比关系,增大输入液压力,可以得到更大的输出扭矩;通过虚拟仿真比较30°、45°、60°系列螺旋角螺旋副的输出扭矩T和导程l的相对关系,在不考虑任何齿轮变位的情况下,45°螺旋角组成的螺旋副传递效率最高,由于摆动液压缸系列化设计的要求,所有斜齿轮的齿顶圆尺寸将优先确定,此时斜齿轮的螺旋角应尽可能的设计在45°附近。在输入液压力一定的情况下,如要得到更大的输出扭矩,优先考虑增大斜齿轮的径向尺寸。
| [1] | Yang S G, Zi B. Design and analysis of a 2-DOF hybrid-driven planar parallel manipulator based on virtual prototype technology[C]//Proceedings of 20102nd International Conference on Signal Processing Systems, July 5-7, 2010, Dalian. Piscataway:IEEE Press, 2010, 3:502-506. |
| [2] | Hu D C, Ye D P. Virtual prototype technology and its application in analysis of cam transmission[C]//Proceedings of 20105th International Conference on Computer Science & Education, August 24-27, 2010, Hefei. Piscataway:IEEE Press, 2010:1053-1057. |
| [3] | Dong J H, Yao X J. Study on dynamic simulation of small planetary ball mill based on virtual prototype technology[C]//Proceedings of 2009 Second International Conference on Intelligent Computation Technology and Automation, October 10-11, 2009, Changsha, Hunan. Piscataway:IEEE Press, 2009:264-267. |
| [4] | Lin Z, Long Y C, FA C, et al. Application of virtual prototype technology to analyzing the kinetic and dynamic characteristics of the base of the remote cylinder[J]. JSME International Journal, Series C Mechancial Systems, Machine Elements and Manufacturing, 2006, 49(1): 247–252. DOI:10.1299/jsmec.49.247 |
| [5] |
梁锡昌, 王光建, 郑小光.
基于螺旋机构的旋转作动器研究[J]. 航空学报, 2003, 24(3): 282–285.
LIANG Xichang, WANG Guangjian, ZHENG Xiaoguang. Research on rotary actuator based on screw device[J]. Acta Aeronautica Et Astronautica Sinica, 2003, 24(3): 282–285. (in Chinese) |
| [6] | Zhang F M, Xiang C L, Liu H. Study on modeling and simulation of spiral bevel gears[J]. Advamced Materials Research, 2011, 154-155: 1292–1295. |
| [7] | 陈淑梅. 液压与气压传动[M]. 北京: 机械工业出版社, 2007. |
| [8] | Wei X T, Du Q, Liu J C. The application of UG NX second development in centrifugal pump impeller vane 3D solid modeling[J]. Applied Mechanics and Materials, 2009, 20-23: 1286–1291. |
| [9] |
徐江敏, 孟慧亮, 苏石川.
渐开线斜齿轮的参数化设计与应用[J]. 计算机应用技术, 2008, 35(11): 33–35.
XU Jiangmin, MENG Huiliang, SU Shichuan. Parameterized designing of involute helical gears based on UG[J]. Technology of Computer Application, 2008, 35(11): 33–35. (in Chinese) |
| [10] | Dooner D B. On the invariance of gear tooth curvature[J]. Proceedings of the Institution of Mechanical Engineers. Part C:Journal of Mechanical Engineering Science, 2006, 220(7): 1093–1096. |
| [11] | Fetvaci C, Imrak C E. Computer modeling and simulation of spur involute gear by generating method[J]. Key Engineering Materials, 2011, 450: 103–106. |
| [12] | Burgermeister B, Arnold M, Esterl B. DAE time integration for real-time applications in multi body dynamics[J]. Zeitschrift Angewandte Mathematik Mechanik, 2006, 86(10): 747–840. DOI:10.1002/(ISSN)1521-4001 |
| [13] | Breukels J, Ockels W J. Analysis of complex inflatable structures using a multi-body dynamics spproach[C]//Proeedings of 200849th Structures, Structural Dynamics, and Materials Conference, April 2008, Schaumburg, IL.Reston:Aerospace Research Central, 2008:2284-2291. |
| [14] | Lang H, Linn J, Arnold M. Multi-body dynamics simulation of geometrically exact cosserat rods[J]. Multibody System Dynamics, 2011, 25(3): 285–312. DOI:10.1007/s11044-010-9223-x |
| [15] | Slavic J, Boltezar M. Nom-linearity and non-smoothness in multi-body dynamics:application to woodpecker toy[J]. Journal of Mechanical Engineering Science, 2008, 220(3): 285–296. |
| [16] | Nikravesh P E. Newtomian-based methodologies in multi-body dynamics[J]. Journal of Multi-body Dynamics, 2008, 222(4): 277–288. |
| [17] | Hu K, Guo Y C. Virtual prototyping of belt conveyor based on recurdyn[J]. Applied Mechanics and Materials, 2009, 16-19: 776–780. DOI:10.4028/www.scientific.net/AMM.16-19 |
| [18] | Liu C C, Chen Y C, Lin S H. Contact stress analysis of straight concave conical involute gear pairs with small intersected angles[C]//Proceedings of the International Multi Conference of Engineers and Computer Scientists, 2010(3):17-19. |
| [19] | 濮良贵, 纪名刚. 机械设计[M]. 北京: 高等教育出版社, 2006. |
| [20] | Donida F, Ferretti G, Savaresi S M, et al. Object-oriented modelling and simulation of a motorcycle[J]. Mathematical & Computer Modelling of Dynamical System:Methods, Tools and Applications in Engineering and Related Sciences, 2008, 14(2): 79–100. |
| [21] | FunctionBay, Inc. RecurDynTM/Solver Theoretical Manual[CP/OL].2008. |
| [22] | FunctionBay, Inc. RecurDynTM/MTT2D/3D[CP/OL].2008. |
| [23] | Dou H S, Khoo B C. Energy loss distribution in the plane Couette flow and the Taylor-Couette flow between concentric rotating cylinders[J]. International Journal of Thermal Sciences, 2007, 46(3): 262–275. DOI:10.1016/j.ijthermalsci.2006.05.003 |
| [24] | 郭晗曦, 张洪东. 摆动液压缸内部结构泄漏分析[C]//第七届(2009)中国钢铁年会论文集(下). 北京: 冶金工业出版社, 2009: 689-693. |
 2014, Vol. 37
2014, Vol. 37

