2. 常州工学院 光电学院, 常州 213002
2. College of Optoelectronic Engineering, Changzhou Institute of Technology, Changzhou 213002, China
视频跟踪是机器视觉研究热点之一,近几十年来引起了众多研究者的关注,提出了大量的跟踪算法,并且已成功应用于视频监控、运动分析和人机交互等领域[1-5]。现有的跟踪算法粗略可以分为2类:确定跟踪算法和随机跟踪算法[6]。确定跟踪算法是以核跟踪[7]为代表,核跟踪最先由Comaniciu把均值移动成功应用到视频跟踪中,具有简单,速度快的特点,但易收敛到局部极小值,且难以跟踪快速运动、姿态快速变化及严重遮挡的目标,而随机跟踪算法则能有效处理该类问题,粒子滤波[8]是该类方法中应用最广泛的方法之一,它能有效地处理非线性非高斯分布的状态预测问题,同时还是一种比较鲁棒的跟踪方法。众多跟踪算法采用固定不变的目标模板进行跟踪,对于姿态快速变化和严重遮挡的目标极易产生漂移。为了避免漂移,Ross等[9]利用子空间方法获取持续变化的目标集代替固定不变的目标模型,但该方法需要提前训练且计算量较大;Leichte Ido等[10]和Bajramovic F等[11]都是采用先验多目标模型代替固定目标模型;Wang等[12]利用混合高斯分布在线构建目标模型,但在实际场景中,很多目标模型分布不适合高斯分布;Kwon J等[13]利用了DSPCA[14]在线构建多参照直方图,但其时间复杂度非常高,不适合实时跟踪。
为了解决上述问题,结合改进后DSPCA在线获取目标图像变化集,将图像集中的图像按照改进后的BRD[15]准则线性融合为单参照颜色直方图。在粒子滤波框架下,使用随机漂移模型作为系统状态转换函数,将相似度函数BRS(bin-ratio-similarity)作为各粒子的权值。实验证明,提出的方法鲁棒地跟踪到快速形态变化及严重遮挡的目标。
1 粒子滤波器简介视频目标跟踪可视为带有隐式状态的马尔科夫状态估计问题,为了有效解决非线性、非高斯状态估计问题,Isard[8]引进了粒子滤波。假设目标状态向量Xt=[x,y]是目标的中心坐标,且状态方程满足一阶马尔科夫p(Xt|X1:t-1)=p(Xt|Xt-1),量测方程用可p(Yt|Xt)表示,其中Yt是量测值,1:t-1表示直到t-1时刻对应值的集合。根据贝叶斯理论,状态的估计值可以通过式(1)迭代求解
| $ \begin{align} &p\left( {{X}_{t}}\left| {{Y}_{1:t}} \right. \right)\approx p\left( {{Y}_{t}}\left| {{X}_{t}} \right. \right)\int{p\left( {{X}_{t}}\left| {{Y}_{t-1}} \right. \right)} \\ &\ \ \ \ \ \ \ \ \ p\left( {{X}_{t-1}}\left| {{Y}_{1:t-1}} \right. \right)\text{d}{{X}_{t-1}}。\\ \end{align} $ | (1) |
后验分布p(Xt|Y1:t)可以用蒙特卡罗方法近似表示p(Xt|Y1:t)≈{xti, wti}tN=1,其中,Xti表示t时刻对应的第i个粒子的状态,wti表示第i个粒子状态所对应的权重,可以通过式(2)迭代获得。
| $ w_{t}^{i}\approx _{t}^{i-1}p\left( {{Y}_{t}}\left| X_{t}^{i} \right. \right)\ \ \ \text{S}.\text{T}.\ \ \ \ \sum\nolimits_{i=1}^{{{N}_{s}}}{w_{t}^{i}}。$ | (2) |
具体的采样、量测似然及重采样的理论可以参照文献[16]。
2 多参照颜色直方图固定参照颜色直方图易产生跟踪漂移,为了改善这一问题,文中仍采用单参照直方图,但它是从不同目标形态的颜色直方图中计算。不同目标形态是利用DSPCA[14]构建,具体将在2.1中讨论。2.2介绍多参照颜色直方图。
2.1 稀疏主成分分解假设At是Gramian矩阵,e是稀疏主成分且满足(5)式。
| $ \text{Maximize}\ {{e}^{\text{T}}}{{A}_{t}}e-\lambda \left| e \right|_{0}^{2}\ \ \ \ \ \text{s}.\text{t}.\ \ \ \ \ {{\left\| e \right\|}^{2}}=1, $ | (5) |
其中,|e|0是0阶范式,也就是列向量e中非零的个数;λ是控制参数,用来控制e的稀疏程度,λ值越大,e越稀疏。在文中,t时刻的Gramian阵At可以通过式(6)计算。
| $ \begin{align} &\ \ \ \ \ \ \ \ \ {{A}_{t}}={{s}^{\text{T}}}S, \\ &s=\left[f_{t}^{1}\cdots f_{t}^{i}\cdots f_{i}^{{{N}_{s}}} \right], \\ \end{align} $ | (6) |
其中:fti是t时刻的灰度图;Ns是灰度图像像素数;为了求解稀疏主成分e,利用文献[4]的优化工具,可以获得式(6)近似解。在所有成分中,按照式(7)选出r个成分向量er。
| $ I_{t}^{r}=\left\{ i_{a}^{b}\left| i_{a}^{b} \right. \right\}=\left. s\left( y \right),{{e}_{r}}\left( y \right)=0 \right\}。$ | (7) |
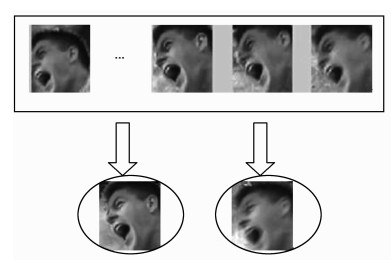
如果er(y)的第y个元素是一个非零值,Iti就包含式(6)中的矩阵s所对应列的第y个灰度图所对应的HSV图。具体的分解过程如图 1所示。
|
图 1 灰度图像的DSPCA分解过程 |
通过稀疏主成分分解获得目标形态集,需要将形态集中的图像合成一个参照直方图。在合成时,采用改进BRD[15]准则(也就是BRS)进行线性系数化。由于跟踪初始化时,已确定参照直方图qu是一个U bin的直方图。先将目标形态集中的图像按照文献[7]分别进行计算对应的颜色直方图pmu(m=1, …, M),接着对所有的直方图归一化,即满足。
| $ \sum\limits_{u=1}^{U}{{{\left\| p_{m}^{u} \right\|}^{2}}}=1。$ | (8) |
对于目标直方图q和候选目标直方图p,他们的相似性可以通过式(9)计算。
| $ d=\frac{\left\| p+q \right\|_{2}^{2}\sum\nolimits_{u=1}^{N}{\frac{{{p}_{u}}{{q}_{u}}}{{{\left( {{p}_{u}}+{{q}_{u}} \right)}^{2}}}}}{{{n}_{e}}}, $ | (9) |
其中:N是直方图量化的bin数;Ne是有效bin数,即也就是2个直方图量化空间和不为零的个数。
假设形态集中有M幅图像,其对应的直方图qk,对于t时刻的参照直方图可以利用下式进行计算。
| $ {{q}_{t}}=\sum\limits_{k=1}^{M}{{{\alpha }_{k}}{{\alpha }_{k}}, } $ | (10) |
其中:αm是稀疏图像集中的第m个图像直方图和q的BRS距离,并且满足,∑m=1Mαm=1。其中M是可变的,文中最大值设为5,如果形态集中的图像多于5,就采用先进先出的原则替换形态集中的目标图像。
3 基于DSPCA的跟踪算法伪码上面主要讨论了基于多参照图跟踪算法的粒子滤波框架和在线获取的目标参照直方图。这一节将给出算法的伪码和复杂性分析。
3.1 算法伪码1) 初始化,令t=0,在初始帧中,手动选取参考视觉目标,并将颜色空间变换成HSV空间,计算参考目标的颜色分布{qu}u=1…U,根据先验分布p(x0),建立初始状态样本集{ X0i,1/N }i=1…N,num=1;For t=1,2,3,…
2) 粒子采样:根据预测高斯分布采样
| $ \widetilde{X}_{t}^{i}\sim q\left( X_{t}^{i}\left| X_{t-1}^{i}, {{Y}_{t}} \right. \right)=N\left( X_{t}^{i}\left| P_{t}^{i} \right. \right)。$ | (11) |
3) 粒子的权值计算:根据式(4)计算样本
4) 视觉目标状态输出:计算t时刻目标状态的MMSE估计
5) 如果num等于25,按照式(7)进行DSPCA分解,获得其稀疏主成份目标形态集,通过式(10)获取新参照直方图;
6) k=k+1,返回2)。
3.2 算法复杂性针对文中算法, 复杂性主要受到DSPCA目标更新和粒子滤波跟踪两方面制约,因此可以从这2个方面进行分析:1)在DSPCA目标更新阶段,所需复杂度为
为了验证上述跟踪算法的有效性和鲁棒性, 选用4段来自韩国首尔大学计算机视觉研究室[13]的视频序列。4个实验都是在带有优化的Mex C++的Matlab2009a,主频为AMD 2.9 GHz四核PC机中执行。实验中,先手动获取25帧的目标图像,然后进行DSPCA分解, 其稀疏控制参数λ取100;每个颜色通道取8 bin,粒子采样状态个数为50。经典粒子滤波每个颜色通道量化成16 bin,粒子采样数也为50;视觉分解跟踪算法采用作者的源码;多特征自适应融合算法用Matlab2009a实现。
第1个实验是篮球赛视频序列,被跟踪的目标是穿绿衣的运动员。在整个序列中,被跟踪的运动员在运动过程中频繁出现遮挡、快速运动、相似目标干扰等变化。该序列长度为686帧,每帧图像的大小为640×352,运动员大小为40×38。对于该实验,文中跟踪算法(MPF)处理速度平均为10 fps(帧/秒), 基本粒子滤波跟踪算法(BPF)处理速度平均为20 fps(帧/秒), 图 2显示了该实验的跟踪结果,其中(a)显示了MPF跟踪结果,(b)是BPF跟踪结果。

|
图 2 实验的跟踪结果 |
采用BPF进行跟踪,在423帧时由于其附近队友经过时,使得跟踪模板发生了严重漂移,到423帧后,跟踪模板几乎完全偏离目标,这是因为目标在运动过程中目标形态不断变化及相似目标的影响,固定目标模型就不能适应这些变化,使得基于固定目标模型的方法失效。相反基于多参照颜色直方图的跟踪性能优于BPF, 特别是在目标快速运动造成的形态变化及相似目标的影响时,如226帧和653帧,就能一直稳健地跟踪到目标,直至视频结束。主要原因在于:DSPCA获取到互补的形态集,使得能适应变化的目标。
第2个实验是双人滑冰比赛的视频序列,被跟踪的女滑冰运动员经常被男滑冰运动员遮挡、其形态经常发生变化且运动比较快。该序列长度为707帧,每帧图像的大小为640×352,被跟踪的女滑冰员的大小为152×52,对于该实验,MPF处理速度平均为10 fps(帧/秒), BPF处理速度平均为20 fps(帧/秒)。图 3显示了该实验的跟踪结果,其中(a)显示了MPF跟踪结果,(b)是BPF跟踪结果。BPF只能跟踪到290帧,由于女滑冰移动比较快,跟踪器慢慢漂移,到298帧时已偏移到男滑冰的身上,而MPF就能鲁棒准确跟踪到707帧。

|
图 3 快速移动,遮挡和形态变化双人滑冰视屏的跟踪结果 |
每个实验(a)中的参照直方图一直是在线更新,因而所提出的算法都能稳健准确跟踪到目标,特别是当目标被遮挡,快速运动或者相似目标相似的干扰,都能稳健跟踪。相反每个实验(b)所用的参照直方图一直保持不变,因而(b)在目标遮挡、快速运动及相似目标的干扰,就不能稳健跟踪到目标,要么误跟踪,要么跟丢目标。
在序列3中(见图 4),被跟踪的运动员头部由于快速运动,存在着遮挡,及相似运动员的干扰。文中方法和视觉分解跟踪方法都能鲁棒地跟踪到目标,但平均速度明显优于视觉分解跟踪速度,为20帧/秒,而视觉分解跟踪的平均速度仅为1.5帧/秒,完全不能实时。

|
图 4 文中方法和视觉分解跟踪方法[13]在快速移动,遮挡等足球序列中的跟踪结果 |
序列4是跟踪人脸结果(见图 5)。歌星在唱歌时头部不断发生变化,同时还受到灯光的不断干扰,在整个330帧序列中,文中方法可以鲁棒地跟踪到目标,而多特征自适应融合跟踪方法仅可跟踪到80帧,然后就慢慢偏离目标。该方法在该序列的平均速度为20帧/秒,而多特征融合跟踪是15帧/秒。

|
图 5 文中方法和多特征自适应融合跟踪方法[17]在演唱会序列的跟踪结果 |
为了进一步量化2种跟踪算法的性能,利用目标跟踪误差进行量测。所谓跟踪误差就是指在二维图像上真实目标的中心位置坐标p和跟踪预测的中心位置坐标p′的距离[16],即
| $ err=\sqrt{{{\left( {{p}_{x}}-p{{'}_{y}} \right)}^{2}}+{{\left( {{p}_{y}}-p{{'}_{y}} \right)}^{2}}}。$ |
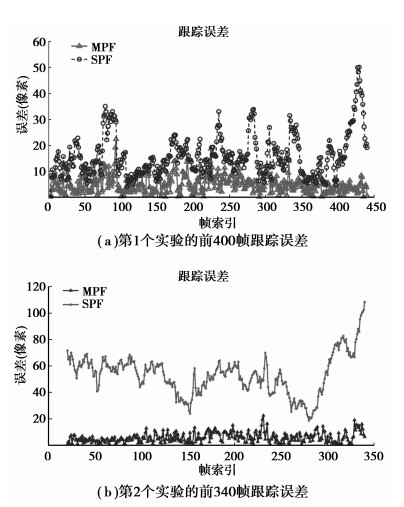
图 6是这2种跟踪算法在这2个视屏序列中的跟踪误差。图 6(a)是第1个实验的前400帧跟踪误差,图 6(b)是第2个实验的前340帧跟踪误差。从图 6(a)中可以看出,由于场景比较简单,因而所提出跟踪算法与所经典粒子滤波跟踪算法都能跟踪到目标,但MPF更精确,误差更小。图 6(b)是在复杂的场景中,提出的跟踪算法与经典粒子跟踪算法相比在稳健性方面有明显的优势,在298帧以后,BPF就跟错目标,跟丢目标。
|
图 6 MPF和BPF目标跟踪误差 |
提出了一种在线更新目标模型的跟踪算法。在跟踪中,借助稀疏主成分分解获取互补的图像集,同时将其按照BRS准则线性融合作为新的目标模型。通过2段运动视频序列的目标跟踪可以发现该方法的稳健性,尤其在目标严重遮挡、姿态不断变化和快速移动时,更能体现;同时,对比实验也表明该方法在复杂场景中优于经典粒子滤波跟踪算法和多特征自适应融合算法,和视觉分解跟踪方法相当,但平均速度明显优于视觉分解跟踪速度,经过优化以后,可以达到实时,而视觉分解跟踪完全达不到实时,平均每帧需1.5~3 s处理。此外,仍有待进一步提高的是多目标跟踪方法研究,这将是后续的研究课题。
| [1] | Nguyen Q D, Milgram M. Online subspace learning using a misalignment detection for tracking a talking face in video sequence[J]. Neurocomputing, 2010, 73(10/12): 1624–1630. |
| [2] | Candamo J, Shreve M, Goldgof D B, et al. Understanding transit scenes:a survey on Human behavior-recognition algorithms[J]. IEEE Transactions on Intelligent Transporta-tion Systems, 2010, 11(1): 206–224. DOI:10.1109/TITS.2009.2030963 |
| [3] | Lucena M, Fuertes J M, Blanca N P, et al. Tracking people in video sequences using multiple models[J]. Multimedia Tools And Applications, 2010, 49(2): 371–403. DOI:10.1007/s11042-009-0376-7 |
| [4] |
蒋蔚, 伊国兴, 曾庆双.
基于SVM数据融合的实时粒子滤波算法[J]. 系统工程与电子技术, 2010, 32(06): 1191–1194.
JIANG Wei, YI Guoxing, ZENG Qingshuang. Real-time particle filter based on data fusion with support vector machines[J]. Systems Engineering and Electronics, 2010, 32(06): 1191–1194. DOI:10.3969/j.issn.1001-506X.2010.06.018 (in Chinese) |
| [5] |
韩松, 张晓林, 陈雷, 等.
基于改进高斯粒子滤波器的目标跟踪算法[J]. 系统工程与电子技术, 2010, 32(6): 1191–1194.
HAN Song, ZHANG Xiaolin, CHEN Lei, et al. Object tracking method based on improved Gaussian particle filter[J]. Systems Engineering and Electronics, 2010, 32(6): 1191–1194. (in Chinese) |
| [6] | Yilmaz A, Javed O, Shah M. Object tracking:A survey[J]. ACM Computing Surveys, 2006, 38(4): 352–355. |
| [7] | Comaniciu D, Ramesh V, Meer P. Kernel-based object tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5): 564–577. DOI:10.1109/TPAMI.2003.1195991 |
| [8] | Isard M, Blake A. Condensation-conditional density propagation for visual tracking[J]. International Journal of Computer Vision, 1998, 29(1): 5–28. DOI:10.1023/A:1008078328650 |
| [9] | Ross D A, Lim J, Lin R S, et al. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision, 2008, 77(1/3): 125–141. |
| [10] | Leichter I, Lindenbaum M, Rivlin E. Mean shift tracking with multiple reference color histograms[J]. Computer Vision and Image Understanding, 2010, 114(3): 400–408. DOI:10.1016/j.cviu.2009.12.006 |
| [11] | Bajramovic F, Deutsch B, Grassl C, et al. Efficient adaptive combination of histograms for real-time tracking[J]. Eurasip journal Journal on image Image and video Video processing Processing, 2008(5): 1–11. |
| [12] | Wang H Z, Suter D, Schindler K, et al. Adaptive object tracking based on an effective appearance filter[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(9): 1661–1667. DOI:10.1109/TPAMI.2007.1112 |
| [13] | Kwon J, Lee K M. Visual tracking decomposition[C]//Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, June 13-18, 2010, San Francisco, CA. Piscataway:IEEE Press, 2010:1269-1276. |
| [14] | Daspremont A, Ghaoui E L, Jordan M, et al. A direct formulation for sparse PCA using semidefinite programming[J]. Siam Review, 2007, 49(3): 434–448. DOI:10.1137/050645506 |
| [15] | Xie N H, Ling H B, Hu W M, et al. Use bin-ratio information for category and scene classific-ation[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, June 13-18, 2010, San Francisico, CA. Piscataway:IEEE Press, 2010:2313-2319. |
| [16] |
程建, 周越, 蔡念, 等.
基于粒子滤波的红外目标跟踪[J]. 红外与毫米波学报, 2006, 25(2): 113–117.
CHENG Jian, ZHOU Yue, CAI Nian, et al. Infrared object tracking based on particle filters[J]. Journal of Infrared and millimeter Waves, 2006, 25(2): 113–117. (in Chinese) |
| [17] |
尹宏鹏, 柴毅, 匡金骏, 等.
一种基于多特征自适应融合的运动目标跟踪算法[J]. 光电子.激光, 2010, 21(6): 917–922.
YIN Hongpeng, CHAI Yi, KUAN Jinjun, et al. A moving target tracking algorithm based on adaptive multiple cues fusion[J]. Journal of Optoelectronics Laser, 2010, 21(6): 917–922. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

