2. 高速公路养护技术交通行业重点实验室, 济南 250031
2. Key Laboratory of Expressway Maintenance Technology of Ministry of Transport(Jinan), Jinan 250031, China
沥青路面材料参数是路面设计研究工作的主要内容,在以弹性层状体系理论为基础的沥青路面设计方法中,材料参数的取值对路面设计结果有很大的影响[1-2]。而在路面材料参数中,路面材料模量是路面设计研究的基础问题,但由于路面材料组成和性质的多变性,及其对湿度、温度和应力依赖性和使用过程中路面材料性能的衰减变化,准确选取路面材料的模量一直是困扰研究和设计人员的难题[3]。路面结构模量更加真实反映沥青路面结构力学特性和路面材料性状,但与实验室材料模量试验受力条件和环境条件的理想化、简单化不同,路面结构模量的获取较为复杂,需要在现场进行测试。基于FWD弯沉盆的路面结构层模量反算为路面结构模量的确定提供了一个新的途径,已成为获取路面结构模量的有效技术手段[4]。由于FWD反算模量并不等于实验室模量,为了与现行路面结构设计参数取值相统一,需对FWD反算模量建立系数进行调整,以便可以通过FWD无损检测数据进行路面结构设计。虽然近年来不少学者研究了沥青层FWD反算模量及其温度修正系数[5-9],但路面FWD反算模量与室内试验材料测试模量之间的关系缺乏研究,造成室内模量与现场模量的脱节,不利于路面结构的分析,且沥青路面在不同损伤阶段的材料模量也存在差异,此方面的研究亦是空白。
解决上述问题的技术措施通常需要铺筑实体工程试验路,在路面使用过程中进行跟踪观测和FWD弯沉检测,分析路面结构在不同破坏阶段的结构模量,但这种试验需要投入大量的人力、财力和物力,需要花费几年至十几年的时间,操作难度很大。修建足尺试验路并进行路面加速加载试验是解决上述问题的有效措施之一,它克服了野外实体工程路面试验周期长、耗资大等缺陷,成为解决FWD反算模量换算系数研究的最有效方法和技术手段。文中通过铺筑不同结构的足尺直道试验路,对其进行加速加载疲劳破坏试验,基于分层弯沉检测和跟踪检测试验路不同损坏程度的路面FWD弯沉,分析FWD反算模量随荷载大小、位置和温度的变化规律,研究级配碎石基层沥青路面FWD反算模量与室内动态模量的换算系数,为路面结构设计和分析以及旧路加铺设计提供基础数据和核心依据。
1 足尺试验路加速加载试验与无损检测方案 1.1 足尺试验路路面结构足尺试验路位于山东交通学院路面加速加载实验室内,试验路试槽宽4 m,长50 m,原始土层深约10 m。足尺直道试验路根据沥青层厚度和路基土类型分为4种路面结构[10],每种路面结构长度约为2 m,如图 1所示。
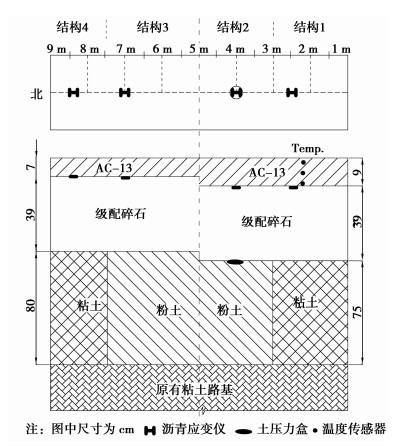
|
图 1 足尺试验路路面结构 |
足尺试验路按照交通部颁布的路基、路面基层和面层施工技术规范进行质量控制,按正常的施工工艺进行施工,并采用水准仪实测了各桩号和各结构层的厚度。试验路修建时,将原始土基挖至路面结构设计深度并夯实,再用粉土和粘土逐层填筑压实(路基土的物性参数见表 1),施工时严格控制每层的含水量,在接近最佳含水量时进行压实,每层压实结束后,立即用灌砂法测定该层的压实度和含水量,其中粉土路基平均压实度为96.5%,粘土路基平均压实度为98%;级配碎石采用规范推荐的连续级配,现场取料筛各筛孔通过率如表 2所示,最佳含水量为5.68%,最大干密度为2.223 g/cm3;沥青混凝土采用AC-13沥青混合料,其体积参数如表 3所示。
| 表 1 路基土的物性参数 |
| 表 2 级配碎石级配组成 |
| 表 3 现场沥青混合料体积指标 |
足尺试验路采用可移动直线式路面加速加载实验系统(accelerated loading testing,ALT)进行疲劳破坏试验,如图 2所示。
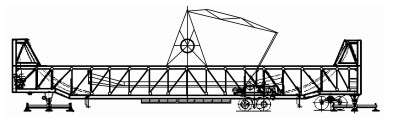
|
图 2 直线式路面加速加载试验设备ALT |
ALT采用单向加载方式,依靠单侧单轴或单侧双联轴施加荷载,加载有效长度为9 m,最大单轴轴载为280 kN,有效运行速度10~26 km/h,每天可向路面施加约6 000~9 000次轮载作用。轮胎为子午线全钢丝胎,轮胎直径1.03 m,双轮组轮隙宽度11 cm,能自动实现横向偏移从而模拟实际道路行车荷载的轮迹分布,再现货车轮胎荷载对路面的破坏作用。试验采用22 km/h的运行速度单侧单轴集中加载,轮载无横向分布,单轴轴载设为165 kN(单侧双轮荷载为82.5 kN),胎压为1.0 MPa,每加载循环1次历时约11 s,与实际公路荷载间歇时间基本一致。
2009年10月~2010年11月完成疲劳加载试验,共施加单轴荷载905 246次,考虑轮载横向分布及轴载当量换算,相当于路面作用标准轴载次数为905 246×2.03×(165/100)3.97=134 175 71次。因加速加载试验位于室内,路面不直接受太阳照晒和降雨的影响,在路面加载期间,实测了每小时路面温度变化(见图 3)。可知,路面温度在15~27 ℃区间占了很大比重,通常认为路面发生疲劳开裂的温度为15~25 ℃,温度较高或较低都不利于裂缝的产生,可见路面温度基本符合沥青混凝土疲劳试验的环境条件。
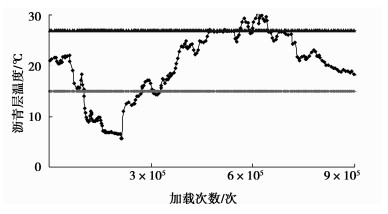
|
图 3 加载过程中路面温度变化 |
依托级配碎石基层沥青路面加速加载足尺试验路,应用分层检测分析方法逐层检测了路面结构层的弯沉[1],并同时记录气温、沥青层温度、级配碎石基层和路基湿度参数。利用实测的FWD弯沉盆,反算不同应力水平下的结构层模量。其次,为了研究路面结构强度变化规律和沥青混合料模量衰变规律以及随温度的变化规律,在不同的加载阶段,进行路表FWD弯沉检测。
采用的FWD弯沉检测方案如下:
1) 试验路修建过程中,定点逐层检测FWD弯沉,同时记录结构层的温度和湿度。对土基采用直径D45 cm承载板,施加5级荷载,分别为215、280、350、424、470 kPa。级配碎石层顶采用直径D45 cm承载板,施加4级荷载,分别为210、280、350、420 kPa,路基和级配碎石基层FWD弯沉传感器按表 4布置。
| 表 4 路基和级配碎石基层FWD传感器分布 |
对沥青层FWD检测采用直径D30 cm承载板,采用三级荷载,分别为566、707、848 kPa,每级荷载重复3次试验,即每个测点需要施加9次FWD荷载,弯沉传感器共有9个,按表 5布置。
| 表 5 沥青层FWD传感器分布 |
2) 季节性或周期性FWD弯沉检测。检测是在路面建成后进行,每隔一段时间,在固定测点进行FWD弯沉检测,了解温度变化和路面结构性能衰变对结构层模量的影响。
3) FWD荷载动力响应测试。在每个传感器埋设点的路面上进行FWD检测,同时采集FWD荷载引起的应力或应变响应。
2 沥青层反算模量及换算系数为使FWD无损检测能准确评价路面的承载能力,应对FWD反算得来的模量值进行换算,以使反算模量可以更好的与室内模量测试值统一。定义FWD反算模量换算系数K为实验室模量与结构层反算模量的比值,即K=E室内/E反算,其中E室内是通过试验室测试或者预估模型所得的模量值,E反算是通过反算程序对FWD弯沉盆进行反算所得的模量值。由于不同材料的特性不同,所以各种材料的反算模量修正系数K的取值以及变化规律是不同的。
2.1 沥青层FWD模量反算基于弹性层状体系理论,采用迭代法反演各结构层模量。但目前迭代法反演路面结构层模量都存在一定缺陷,特别是当分层较多,或结构层太薄(小于75 mm)时反算所得到的数据偏差较大,而且离散性也很大。一般认为,当路面结构分层在4层及4层以下时得到的数据具有一定的可比性[1]。足尺试验路结构层模量采用美国华盛顿州的EVERCALC5.0软件进行反算,将足尺试验路路面结构分为3层,即路基、级配碎石层和沥青面层,FWD检测位置各结构层厚度如表 6所示,反算时采用5tFWD荷载检测的弯沉盆数据。
| 表 6 FWD检测位置结构层厚度 |
在足尺试验路快速加载试验中,在沥青层顶共进行了5次FWD弯沉检测,分别为开始运行、加载至37 538、119 963、218 287、704 120次。进行FWD测试时准确记录沥青层温度,以保证模量反算的准确性和有效性,5次FWD弯沉测试反算的各结构层模量列于表 7。
| 表 7 足尺路面不同加载次数下的结构层反算模量 |
从表 7不同加载次数结构层FWD反算模量可以看出:
1) 粘土路基反算模量值较为稳定,结构1粘土路基模量均值为203.4 MPa,结构4粘土路基反算模量均值为220.1 MPa;对于粉土路基结构,在加载的初期阶段,结构2和结构3基本不变,约185~190 MPa,加载至末期(约70万次时),模量均有所增加,反算模量值为215~220 MPa,增幅为12%~18%。
2) 级配碎石层模量变异性较大,结构1和结构4级配碎石层模量在加载初期,随加载次数缓慢增大后减小;结构2和结构3级配碎石层模量在加载初期随加载次数增加略有增长,而后保持稳定,加载末期,级配碎石层模量均有所降低,但降幅较小。
3) 沥青混合料是一种感温性较强的粘弹性材料,温度的变化对沥青层模量有着重要的影响。从图 4沥青层模量随加载次数的变化可以看出,随路面温度的降低,反算沥青层模量增大,随温度升高而减小。结构1、结构2和结构3均表现出了一致的规律性,且模量值大致相等;结构4沥青层模量值较其他结构差异较大,与该结构沥青路面被切割后埋设动态称重系统相关。
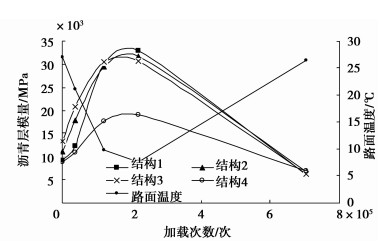
|
图 4 沥青层模量随加载次数的变化 |
参考AASHTO TP62试验方法,采用常应变控制方式,对旋转压实成型的圆柱体试件施加连续正弦荷载,测试沥青混合料试件在规定试验条件下的动态模量,整个试验过程在弹性工作范围内进行,试件经受动荷载的重复作用。
文中通过旋转压实仪成型了与现场路面相同空隙率的圆柱体试件,然后将试件取芯、切割成Φ100 mm×150 mm圆柱体试件,采用SPT简单性能试验机测试了AC-13沥青混合料试件在不同温度时的动态回弹模量。动弹模量的测试加载频率为10 Hz,试验温度分别为5、10、15、20、30、40 ℃,根据动态模量试验结果进行动弹模量与温度的回归分析,即可得到沥青混合料动态回弹模量随温度变化而变化的曲线方程,如式(1)所示。根据回归的动态模量随温度变化的方程,即可计算出任意温度条件下沥青混合料的动态模量,表 8给出了FWD路表弯沉测试时沥青层材料的动态回弹模量。
| $ E\text{=}313\ 53\ {{\text{e}}^{\text{-0}\text{.0464T}}}, $ | (1) |
| 表 8 沥青层反算模量换算系数K |
式中:E为AC-13沥青混合料动态回弹模量,MPa;T为温度,℃。
2.3 沥青层反算模量换算系数K将实验室沥青混合料动态模量与足尺试验路沥青层反算模量对比,得出FWD弯沉检测温度时的沥青层反算模量换算系数K,如表 8所示。
由表 8可以看出,沥青层反算模量换算系数K随荷载作用次数的增加先减小而后增大,这与沥青层模量的衰变规律相吻合。路面未施加轮载前,模量换算系数K=0.70~1.01;轮载作用37 538次时,沥青层模量修正系数较未加载前反而有所降低,这与面层沥青混合料被行车荷载的进一步压实有关;加载至704 120次时,模量换算系数K=1.31~1.50,此时足尺试验路各结构轮迹带已出现了自顶向下发展的纵向裂缝,除了结构3沥青层层底开始出现结构性开裂外,其余结构均未发生结构性开裂,因此,当沥青层层底开始出现疲劳开裂时,沥青层FWD反算模量换算系数K>1.50。
3 级配碎石基层模量反算与换算系数 3.1 级配碎石层模量反算级配碎石基层严格按照施工技术规范施工,压实后表面稍干即撒铺乳化沥青,在其表面进行FWD弯沉检测。检测时采用45 cm直径的承载板,荷载应力水平采用210、280、350、420 kPa 4级荷载,每个应力水平作用3次。
在级配碎石顶进行FWD弯沉测试时,将路面结构划分为路基和级配碎石层两层,基于迭代法进行路面结构层模量反演。在反算过程中,对于反常的弯沉盆数据予以剔除,反算结果如表 9所示。
| 表 9 级配碎石基层顶FWD反算模量 |
由表 9反算结果可知,级配碎石基层和路基的模量均随应力水平升高而降低,但受应力水平的影响并不明显。在210 kPa的应力水平时,反算值反而减小,这可能跟级配碎石材料的松散特性及结构层上并无其他结构层的约束有关。
通过级配碎石顶FWD弯沉检测可知,在280 kPa应力水平时,级配碎石层反算模量约140~150 MPa,粘土路基反算模量约190~200 MPa;粉土路基反算模量约140~150 MPa。可见,随着级配碎石层的铺筑,在级配碎石顶反算的路基模量较路基顶FWD反算的路基模量值要大,符合路基模量随应力水平变化的规律。
3.2 级配碎石层反算模量换算系数根据实测的APT试验路级配碎石层底压应力水平,推算级配碎石层1/3深度位置偏应力和围压,结合现场取料制备试件的室内UTM重复加载三轴压缩回弹模量试验结果,得出APT试验路级配碎石基层材料室内回弹模量为179.9 MPa[1],将该模量值与相同环境条件下沥青层顶FWD反算的级配碎石层模量值进行对比,得到级配碎石基层的反算模量换算系数(见表 10)。计算结果表明级配碎石层的FWD反算模量小于级配碎石材料室内重复加载回弹模量值,即反算模量换算系数大于1,比值范围为1.32~1.49,也即说明对于级配碎石基层沥青路面结构,级配碎石层的反算模量为室内重复加载试验回弹模量的0.67~0.75。AASHTO2002中指出沥青层下卧层为级配碎石基层(或底基层)时,级配碎石层反算模量与室内重复加载回弹模量的比值为0.67[1],因此,级配碎石层反算模量换算系数与级配碎石所处的层位以及路面结构类型相关,文中计算结果与AASHTO2002设计指南基本一致。
| 表 10 级配碎石基层反算模量换算系数K |
路基回弹模量是表征路基抗变形能力及路面结构设计的重要力学参数,对路基路面结构的强度、刚度、稳定性、使用性能和使用寿命起着决定性的作用,其取值大小直接影响着路面结构层的厚度设计和路基路面的施工质量。
研究表明,路基土的压实度和含水量是影响路基土模量的关键因素[13]。路基施工过程中,对每层路基土进行了压实度和含水量检测,严格按照施工技术规范进行施工。因足尺试验路路基土的厚度约10 m左右,在路面结构层模量反算时,可以不考虑路基土底部岩层的影响,将路基作为一个整体结构层考虑。
4.1 路基顶FWD检测与模量反算按照检测计划,在足尺直道试验路施工过程中,每一结构层施工完成后都在其表面进行FWD检测,并采集了温度、湿度和结构层厚度等参数。土基顶面进行了1.0、1.7、5.5、6.5 m桩号的FWD弯沉,采用EVERCALC5.0进行路基模量的反算,结果如表 11所示。
| 表 11 不同荷载作用下路基模量反算结果 |
由表 11可以看出:1)粘土路基或粉土路基的模量随应力水平增大而减小,呈现出应力弱化的特征。按照上述规律,当路基顶应力水平为35 kPa时,粘土路基的模量约173 MPa,粉土路基模量约100 MPa;2)应力水平对路基模量的影响不大,应力水平增大1倍,路基模量仅减小9.4%,说明应力水平对路基模量的影响较小。
4.2 土基材料模量换算系数FWD反算结果表明,土基材料的反算模量随着路面结构层厚度的增加而增大,而室内模量试验值也是随着路面结构层厚度的增大而增大的,但是增加的幅度小于反算模量增加的幅度。
以土基材料的室内重复加载回弹模量值以基准,与土基顶FWD弯沉反算模量(见表 11)、级配碎石层顶FWD弯沉反算模量(见表 9)和沥青层顶FWD弯沉反算模量(见表 7)中的路基反算模量值进行对比,得到土基材料的反算模量换算系数,如表 12所示。
| 表 12 土基材料的反算模量换算系数K |
由表 12可以看出,随FWD检测层位的不同,路基反算模量换算系数K不同。由路基顶FWD弯沉检测反算路基模量与室内重复加载三轴压缩回弹模量试验结果比较可知,路基无损检测反算模量高于室内重复加载三轴压缩回弹模量值,粉土路基顶FWD检测反算模量换算系数均值为0.34;级配碎石层顶FWD反算路基模量换算系数均值为0.23,沥青层顶FWD反算路基模量换算系数均值为0.18。粘土路基顶FWD检测反算模量换算系数均值为0.42;级配碎石层顶FWD反算路基模量换算系数均值为0.37,沥青层顶FWD反算路基模量换算系数均值为0.31。可见,随着FWD弯沉检测层位的上移,土基反算模量换算系数减小。此外,土基的反算模量与其下卧层刚度和厚度有关,设计者在计算路基模量时,要考虑它代表的是整个路面基础的模量。
5 结论根据足尺试验路结构层厚度测量和环境观测,对试验路进行了FWD弯沉测试,并且对测试结果进行反算,得出如下结论:
结构完好路面的沥青层反算模量换算系数K=0.7~1.0;路面出现Top-down开裂后,K=1.3~1.5;沥青层层底出现疲劳损伤时,K>1.5。
级配碎石基层和路基的模量均随应力水平升高而减小,但受应力水平的影响并不显著。级配碎石层反算模量换算系数与级配碎石所处的层位以及路面结构类型相关:当沥青层下卧层为级配碎石层时,级配碎石层反算模量换算系数为1.32~1.49,与AASHTO2002基本一致。
沥青面层模量受温度和轮载作用次数的影响最大;级配碎石结构层反算模量结果变异性较大,但与现行规范推荐模量和室内重复加载三轴压缩回弹模量相差不大;土基FWD反算模量大于现行规范推荐的静态回弹模量和重复加载三轴压缩回弹模量。
土基反算模量换算系数与其所受的应力水平及土质类型相关,随着FWD弯沉检测层位的上移,土基反算模量换算系数减小。低液限粘土FWD反算模量换算系数变动于0.31~0.42;低液限粉土路基FWD反算模量换算系数变动于0.18~0.34范围内。
| [1] | NCHRP Project1-37A. Guide for mechanistic-empirical design of new and rehabilitated pavement structures Final Repor[R].Final Report Part2 Chapter2:Material Characterization, 2004. |
| [2] | NCHRP. Guide for mechanistic-empirical design of new and rehabilitated pavement structures[R].Final Report, Appendix Ⅱ-1, Calibration of Fatigue Cracking Models for Flexible Pavements, February 2004. |
| [3] | Gedafa D S, Hossain M, Romanoschi S A, et al. Field verification of superpave dynamic modulus[J]. Journal of Materials in Civil Engineering, 2010, 22(5): 485–494. DOI:10.1061/(ASCE)MT.1943-5533.0000048 |
| [4] | Technical Support Services Contractor, LAW PCS. LTPP manual for falling weight deflectometer measurements operational field guide-lines(Version 3.1)[R].Washington D C:Federal Highway Administration, 2000. |
| [5] | Baltzer S, Jansen J M. Temperature correction of asphalt moduli for FWD measurements[C]//Proceedings of the 4th International Conference on the Bearing Capacity of Roads and Airfields, August 17-21, 1994, Minneapolis, MN.[S.l]:ICBCRA, 1994:753-768. |
| [6] |
徐艳玲, 唐伯明, 谢国栋, 等.
基于FWD的沥青层反算模量修正系数[J]. 长安大学学报:自然科学版, 2012, 32(3): 24–29.
XU Yanling, TANG Boming, XIE Guodong, et al. Back calculated modulus correction coefficient for asphalt concrete layer based on FWD[J]. Journal of Chang'an University:Natural Science Edition, 2012, 32(3): 24–29. (in Chinese) |
| [7] | Lukanen E O, Stubstad R, Briggs R. Temperature predictions and adjustment factors for asphalt pavement[R]. Mclean:Federal Highway Administration, Research and Development Tumer-Fairbank Highway Research Center, 2000. |
| [8] |
周亮, 凌建明, 林小平, 等.
沥青层反算模量的温度修正系数[J]. 同济大学学报:自然科学版, 2011, 39(11): 1641–1645.
ZHOU Liang, LIN Jianming, LIN Xiaoping, et al. Temperature adjustment factor for back-calculated modulus of asphalt pavement layer[J]. Journal of Tongji University:Natural Science, 2011, 39(11): 1641–1645. (in Chinese) |
| [9] | Chen D H, Bilyeu J, Lin H H, et a1. Temperature correction on falling weight deflectometer measurements[J]. Transportation Research Record, 2000, 1716(4): 30–39. |
| [10] |
管志光, 庄传仪, 林明星.
足尺沥青混凝土路面加速加载动力响应[J]. 交通运输工程学报, 2012, 12(2): 24–31.
GUAN Zhiguang, ZHUANG Chuanyi, LIN Mingxing. Dynamic response based on accelerated loading testing for full-scale asphalt pavement[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 24–31. (in Chinese) |
| [11] | Timm D H, Priest A L.Material properties of the 2003 NCAT test track structural study[R]. Alabama:National Center for Asphalt Technology Auburn University, 2006. |
| [12] | 庄传仪. 基于加速加载响应的柔性基层沥青路面设计指标与参数研究[D]. 西安: 长安大学, 2012. http://d.wanfangdata.com.cn/Thesis/D308197 |
| [13] | 罗志刚. 路基与粒料层动态模量参数研究[D]. 上海: 同济大学, 2007. http://d.wanfangdata.com.cn/Thesis/W1657837 |
 2014, Vol. 37
2014, Vol. 37


