采用轮毂电机驱动的电动汽车,由于不需要传动装置,结构布置更简单、紧凑,因而更容易实现汽车轻量化,降低制造成本,特别是对于近年来国内外正在研究发展的两人乘坐以下的超微型电动汽车,采用轮毂电机驱动将不存在高电压、大电流、温升等问题限制,具有广阔的市场前景和重要研究价值。目前国内外对电磁离合器的动态特性和优化设计方面进行了一些研究。北京科技大学的张功晖等[1]对汽车座椅的电磁阀进行了动态特性研究,仿真了电磁阀的动态开启时间;哈尔滨工业大学的李勇等[2]对高速运行的无接触式电磁离合器进行了基于磁路法的解析分析和基于Ansoft的仿真计算;合肥工业大学赵韩等[3]采用采用C语言与ANSYS软件相互调用的方法,模拟了电磁离合器的动态过程。奥地利的Jaindl等[4]采用进化算法对电磁流变离合器进行了优化分析等。但目前针对汽车行驶环境特别是轮毂电机内部工作空间下的线圈温升和动态响应时间要求,其电磁离合器动态特性和优化设计研究还较少。
笔者针对超微型电动车轮毂电机电磁驻车制动的新型结构设计,采用电磁计算理论、遗传算法并结合有限元分析对该电磁离合器进行了动态分析和优化设计,以满足采用轮毂电机的超微型电动车驻车制动及其动态响应要求。
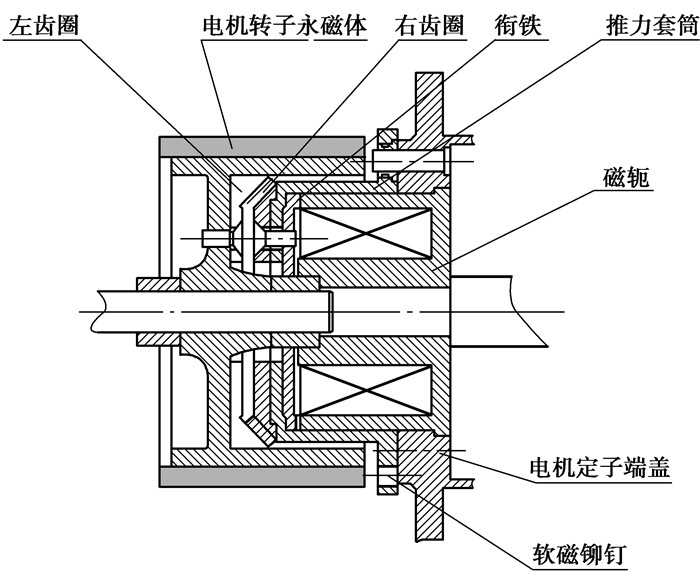
1 新型轮毂电机嵌入式电磁离合器的结构与工作原理图 1所示为一种新型超微型电动车轮毂电机嵌入式电磁驻车制动离合器的基本结构和工作原理图。电磁离合器布置在轮毂电机的转子内,其磁轭固定于电机定子端盖,而衔铁固定于只能横向平移的推力套筒中;该套筒上固定有离合器啮合的右端面齿以及镶嵌有软磁铆钉,该软磁铆钉与转子端面产生吸力作用,而该吸力在套筒靠近左边位置时较小,远离时较大。当微车行驶时,电磁离合器开始产生较大电流以产生足够吸力克服软磁铆钉与转子端面的吸力作用和套筒运动摩擦力而将衔铁贴住磁轭,此时软磁铆钉与转子端面吸力迅速减小而磁轭与衔铁的吸力增大,因此离合器仅通以很小电流就能维持吸合位置而避免过度温升和节省电能。该电磁驻车制动离合器的显著特点是没有压缩弹簧,靠转子的端面吸力产生制动力。当微车断电或长期停驶时,电磁离合器吸力消失,在推力套筒上的软磁铆钉与转子端面吸力作用下,离合器右齿圈与左齿圈结合,转子和与此传动连接的轮胎被卡住实现驻车制动。
|
图 1 电磁离合器结构 |
这种设计结构简单、空间紧凑,但对电磁离合器电磁控制和动态响应要求较高,为此须对电磁离合器结构进行动态特性分析和优化设计研究。
2 静态电磁离合器电磁吸力及优化计算 2.1 电磁离合器的静态计算电磁吸力计算一般采用两种方法:磁路计算法和电磁有限元法。磁路计算法通过分析电磁铁的各项参数,得到等效磁路图,再按照电磁吸力公式计算出电磁吸力。该方法简单易行,计算量小,但由于基于经验公式的简化计算,且忽略了漏磁的影响作用,求解精度较低[5]。电磁有限元方法基于Maxwell方程组,利用数值计算方法求解,其计算精度较高且能够直观把握磁场分布情况。笔者将采用电磁有限元法计算静态电磁吸力,计算的具体理论推导如下[6-7]。
磁场强度H满足安培环路定理,即
| $ \nabla \times \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{J}}, $ | (1) |
磁感应强度B满足高斯磁通定律,即
| $ \nabla \cdot \mathit{\boldsymbol{B}} = 0, $ | (2) |
磁感应强度B和磁场强度H满足本构关系,即
| $ \mathit{\boldsymbol{B}} = \mu \mathit{\boldsymbol{H}}, $ | (3) |
式中:J为电流密度;μ为介质磁导率。由于式(2) 中的B的无散性,引入矢量磁势A,又将式(3) 和式(4) 带入式(1) 得
| $ \nabla \times \left( {\frac{1}{\mu }\nabla \times \mathit{\boldsymbol{A}}} \right) = \mathit{\boldsymbol{J}}。$ | (4) |
对于轴对称问题,采用圆柱坐标系进行分析,此时式(4) 写成偏微分方程形式为
| $ \frac{1}{r}\frac{\partial }{{\partial z}}\left[ {\frac{1}{\mu}\frac{\partial }{{\partial z}}\left( {r{\mathit{\boldsymbol{A}}_\theta }} \right)} \right] + \frac{\partial }{{\partial r}}\left[ {\frac{1}{\mu}\frac{\partial }{{\partial r}}\left( {r{\mathit{\boldsymbol{A}}_\theta }} \right)} \right] + \frac{1}{\mu }{\nabla ^2}{\mathit{\boldsymbol{A}}_\theta } = - {\mathit{\boldsymbol{J}}_\theta }, $ | (5) |
根据边界条件Aθ=Aθ0=0(第一类边界),
| $ \mathit{\boldsymbol{B}} = \nabla \times \mathit{\boldsymbol{A}}, $ | (6) |
最后根据虚功原理可得到静态磁力
| $ \mathit{\boldsymbol{F = }}\frac{{{\rm{d}}\mathit{\boldsymbol{W}}\left( {s,i} \right)}}{{{\rm{d}}s}} = \frac{\partial }{{\partial s}}\left[ {\int\limits_V {\left( {\int_0^H {\mathit{\boldsymbol{B}} \cdot {\rm{d}}\mathit{\boldsymbol{H}}} } \right){\rm{d}}\mathit{\boldsymbol{V}}} } \right], $ | (7) |
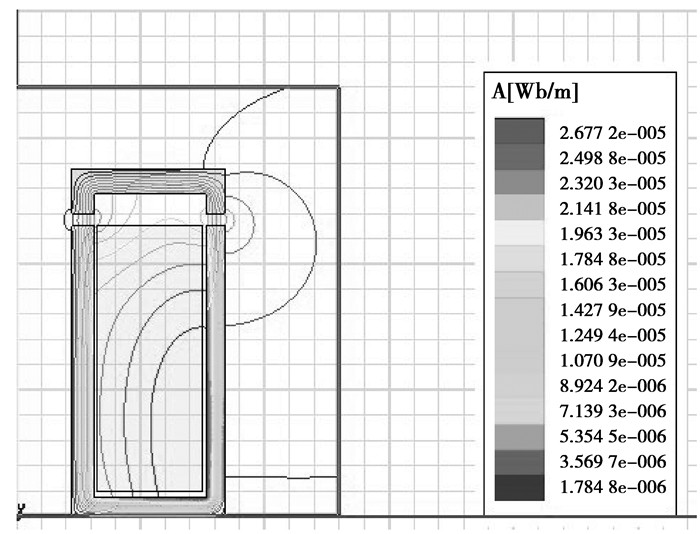
式中:W(s,i)为系统的磁场储能;i为建立磁场的电流,为恒定值。电磁离合器的衔铁和磁轭均采用工业纯铁制造,按照其B-H曲线可得其材料属性。本设计中电磁离合器电源采用24 V的稳压源,设计得到的出离合器线圈匝数为2 310匝,利用Ansoft软件计算出没有优化前电磁离合器气隙长度为1 cm时的电磁力为35.564 N。其磁场分布如图 2、3所示。

|
图 2 电磁离合器电磁感应强度分布云图 |
|
图 3 电磁离合器磁感应线分布云图 |
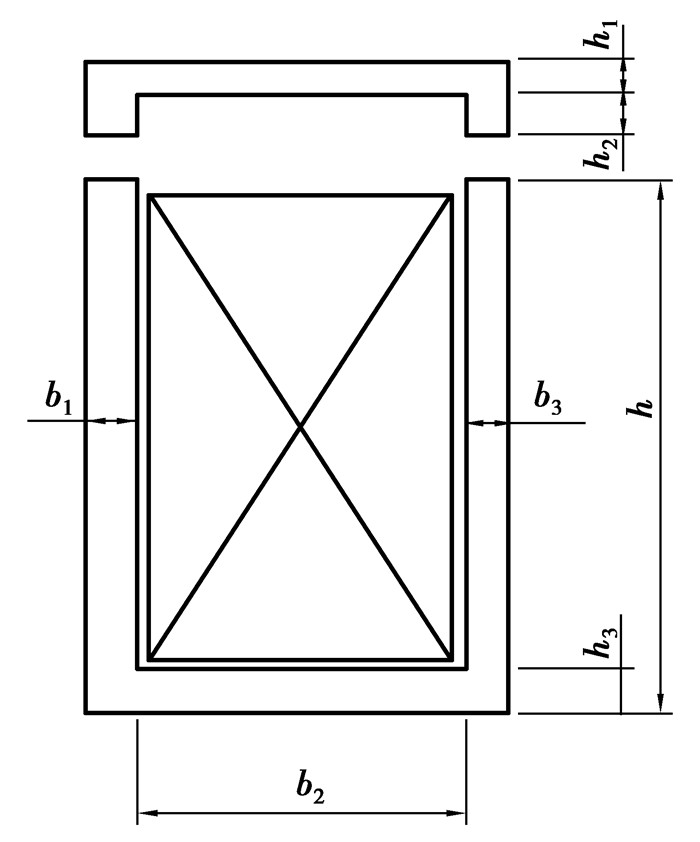
由于所设计的电磁离合器是嵌入于轮毂电机的转子内部,且转子内部空间有限,需要对电磁离合器进行优化,以保证在有限尺寸空间条件下获得最大电磁吸力,以实现驻车制动的离合要求。优化设计方法有很多种,其中遗传算法利用随机化技术来指导对一个被编码的参数空间进行高效的优化方法,它有较强的全局优化能力,是一种自适应的、智能的搜索技术,其主要应用领域是复杂的非线性优化问题。它利用选择、交叉、变异这3个基本操作逐代产生并优选个体(染色体),最终得到优化个体[8-9]。笔者将采用遗传算法对电磁离合器的结构和吸力进行优化。图 4为电磁离合器结构示意图,有7个参数b1,b2,b3,h1,h2,h3,h分别表示如图 4所示。
|
图 4 电磁离合器尺寸参数示意图 |
本文优化的目标是在有限的空间中使得电磁离合器的电磁吸力最大。
1) 优化设计目标函数为电磁吸力F,由公式(7) 所表达,可利用Ansoft通过有限元计算获得。
2) 约束条件包括:
a.磁饱和约束,磁场感应强度不大于纯铁材料的磁饱和强度,B≤Bmax,其中B为磁感应强度,Bmax为材料的磁饱和强度。
b.线圈温升约束,电磁离合器通电线圈产生的温度值小于规定值,即
| $ {\tau _{\rm{x}}} = \frac{{{\rho _{\rm{x}}}{{\left( {IN} \right)}^2}}}{{2{K_{\rm{T}}}{f_{\rm{t}}}{b_{\rm{x}}}h_{\rm{x}}^2}} < 60{}^ \circ {\rm{C,}} $ | (8) |
式中:KT为线圈的散热系数,W/(m2· ℃),一般可以取为9.5~12.7,这里取11 W/(m2· ℃);ft为线圈填充系数;bx为线圈厚度,m;hx为线圈高度,m。
c.边界约束,图 3所示的各个参数均在一定的约束范围内,其长度单位为cm,即
| $ 1.5 < {b_1} < 2.5,8 < {b_2} < 12, $ |
| $ 1.2 < {b_3} < 2.5,1.5 < {h_1} < 3, $ |
| $ 0.5 < {h_2} < 2,1.2 < {h_3} < 3,20 < h < 25。$ |
3) 优化变量:图 3中各个影响电磁吸力大小的结构尺寸参数,b1,b2,b3,h1,h2,h3,h,单位为cm。
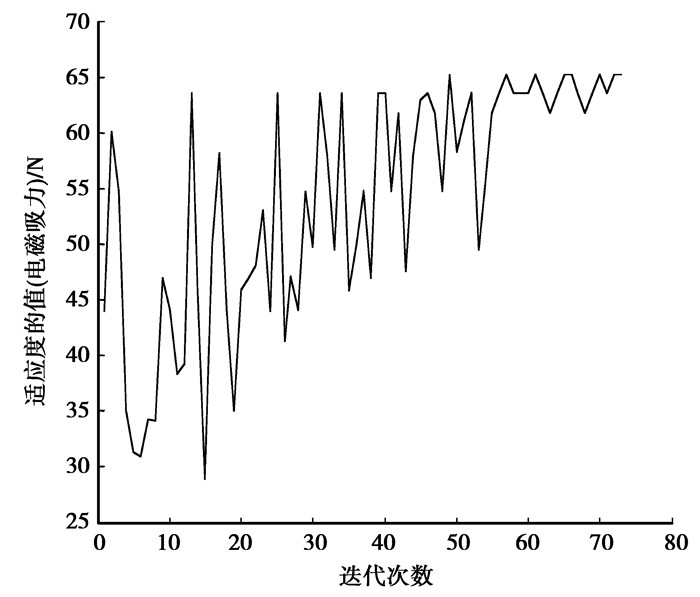
笔者直接采用Ansoft中带有基于遗传算法的优化模块对电磁离合器进行优化,其中选择浮点编码方式,种群中个体数目为20,交叉概率为0.6,变异概率为0.06,最大迭代代数为100,算法终止的条件选择为适应度函数值趋于稳定。图 5为在经过不同代数时适应度值的变化情况。
|
图 5 遗传算法迭代图 |
图 5中横坐标为遗传算法所经过的代数,纵坐标为适应度函数值(电磁吸力),当适应度函数取最大值时,对应要求优化的目标电磁吸力最大。从图中可以看出:当经过73代适应度函数值趋于收敛,也就是大约73代取得全局最优解。计算结果如表 1所示。
| 表 1 优化设计前后参数 |
从表 1中容易看出优化后的电磁力在相同气隙长度条件下比优化前增加了27.6 N。可见采用遗传算法的优化设计获得了良好的效果。
3 电磁离合器的动态模型建立及特性分析 3.1 动态分析理论电磁离合器作为轮毂电机的驻车制动装置,要求电磁离合器有良好的动态响应时间。当电动车准备起动时,轮毂电机控制器将发出指令并给电磁离合器通电,克服电磁反力,将衔铁从转子中吸出,以便起动电机。为满足超微型电动车轮毂电机的操控要求,需要对电磁离合器动态响应时间进行分析计算。为此笔者首先建立了电磁离合器的动态数学模型,该模型中包括电学上的电压平衡麦克斯韦方程[10-13],运动学上的达朗贝尔运动方程。其联立方程组数学表达式为
| $ \left. \begin{array}{l} \frac{{{\rm{d}}\psi }}{{{\rm{d}}t}} = U - IR,\\ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \frac{{{F_x} - {F_f}\left( x \right)}}{m},\\ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = v,\\ \psi \left| {t = 0 = {\psi _0} = 0} \right.,v\left| {t = 0 = {v_0} = 0} \right.,x\left| {t = 0 = {x_0} = 0} \right.。\end{array} \right\} $ | (9) |
式中:U为线圈激励电压;R为线圈电阻;I,Ψ分别为线圈电流和电磁系统全磁链;m为电磁系统运动部件归算为铁心极面中心质量;x为电磁系统运动部件归算为铁心极面中心位移;t为时间;v为运动速度;Fx,Ff为相应折算到铁心极面中心处的动态吸力和运动反力,其中弹簧负载反力是x的函数。
从电磁离合器的动态微分方程组可知其动态响应评价可根据动衔铁位置、电磁铁所产生的动态吸力以及激磁线圈电流参数随时间变化的规律所表达[14-15]。
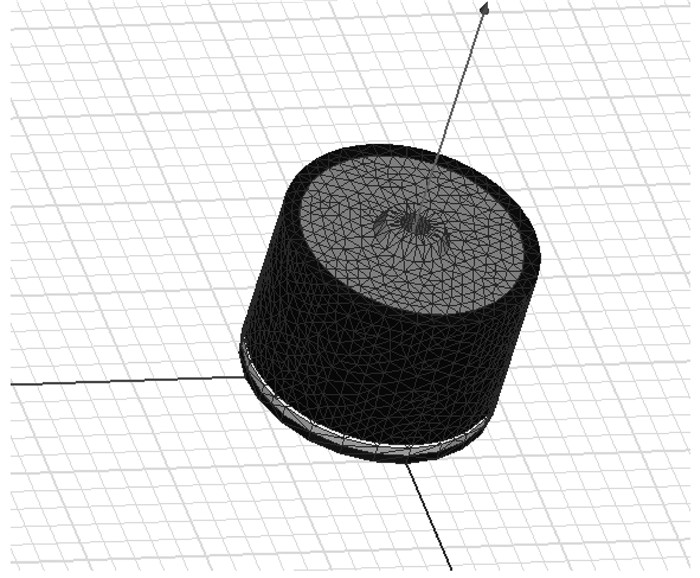
3.2 电磁离合器动态响应计算结果与分析根据前面已经优化好的尺寸数据得到其动态分析的三维模型,将其导入到Maxwell3D中进行计算仿真。图 6为轮毂电机转子和嵌入式电磁离合器的三维有限元模型。
|
图 6 电磁离合器三维有限元模型 |
利用Maxwell瞬态求解器可分析电磁离合器的动态特性和计算其动态响应时间。为此首先需要在几何模型中设置一个band区域,这里将衔铁部分设为band区域,因为只有该区域是运动的,其余均静止。设定的主要运动属性参数如下:运动块质量,m=0.25 kg,初始速度,v=0 m/s。
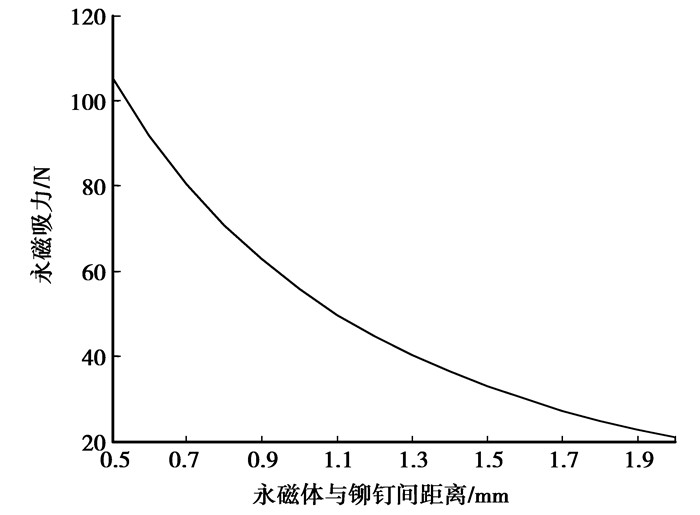
负载力主要由电机转子永磁体与推筒嵌有的铆钉的永磁吸力提供,永磁吸力与气隙的关系如图 7所示。
|
图 7 永磁吸力和气隙大小之间的关系图 |
而该力与运动位移间的关系可通过四次多项式来拟合,由此可得到负载力为
| $ \begin{array}{*{20}{c}} {{F_f} = 14.569{x^4} - 40.554{x^3} + 56.505{x^2} - }\\ {68.468x + 55.881。} \end{array} $ | (10) |
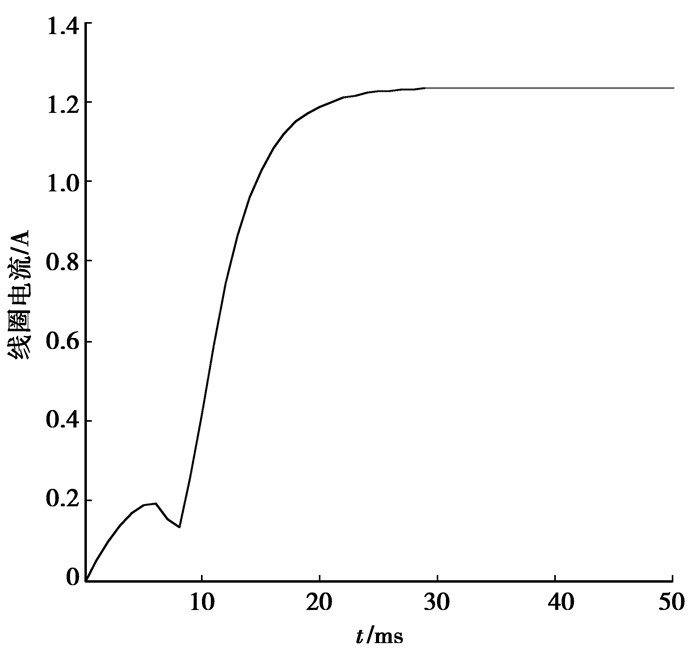
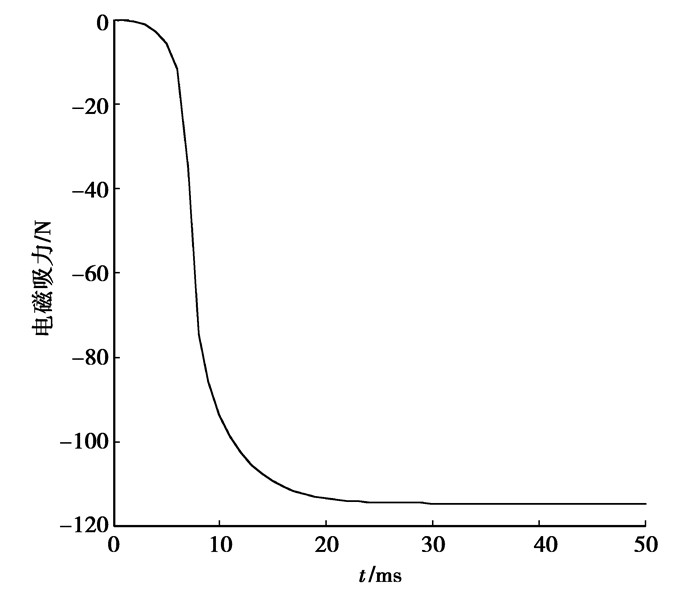
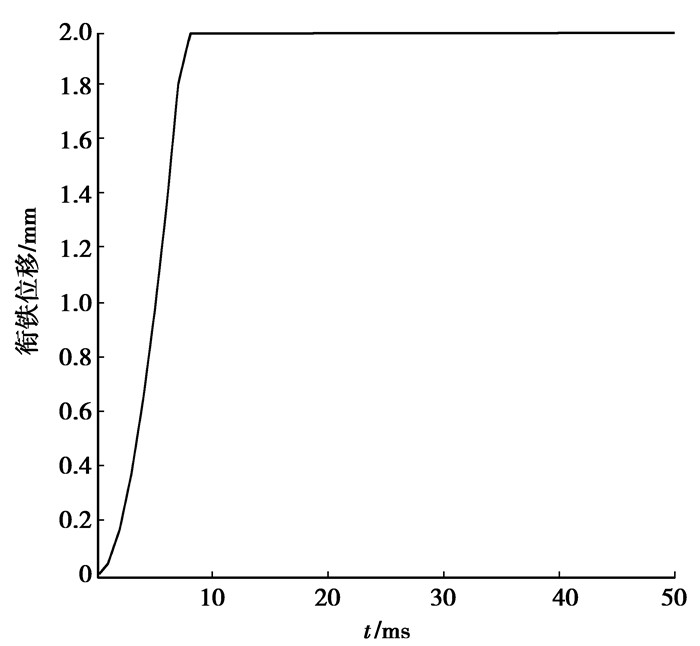
求解计算得到电流、电磁吸力、位移随时间变化的曲线如下图 8、9、10所示。
|
图 8 电流时间关系曲线 |
|
图 9 电磁吸力时间关系曲线 |
|
图 10 位移时间关系曲线 |
从图 8、9、10中可看出:电磁离合器加载24 V电压源时,由于线圈具有较大的电感,电流增加到额定值需要约20 ms时间。大约6 ms时电磁离合器通过电流达到0.2 A,产生的吸力可克服永磁反力,衔铁才开始运动。由于衔铁的运动会产生瞬间反电动势,将阻碍电流的增长,在电流时间曲线中会出现一个波动。波动时间周期大约为3 ms。其后衔铁运动至最小气隙,衔铁处于静止,此时电磁离合器的衔铁和磁轭处于闭合状态,反电动势随即消失,电流又按指数变化增长,直至电流达到1.25 A。随着气隙逐渐减小,衔铁和磁轭之间最大电磁吸力可达到118 N。从上述分析计算可看出,优化设计的电磁离合器,其闭合动态响应时间大约为9 ms,电磁铁的动态特性能够很好满足超微型电动汽车驻车制动的要求。
4 结论1) 采用电磁离合器来实现超微型电动汽车的驻车制动,可简化驻车制动结构并实现操纵的简便化和自动化。
2)利用Ansoft软件建立了电磁离合器的模型,并且采用软件自身的优化功能模块再结合遗传算法对电磁离合器的尺寸和大小进行了优化设计,为其设计提供了理论依据。
3) 通过对优化好的电磁离合器再进行三维的动态分析,所获得的电磁离合器开启和关闭响应时间均能满足超微型电动汽车的驻车制动的设计要求。
| [1] |
张功晖, 黎志航, 周志鸿.
基于Maxwell方程的电磁阀开启过程动态特性仿真研究[J]. 液压气动与密封, 2010, 30(11): 22–23.
ZHANG Gonghui, LI Zhihang, ZHOU Zhihong. Simulation research of dynamic character of solenoid valve's opening process based on Maxwell equation[J]. Hydraulics Pneumatics & Seals, 2010, 30(11): 22–23. DOI:10.3969/j.issn.1008-0813.2010.11.008 (in Chinese) |
| [2] |
李勇, 邢敬娓, 韩素芳, 等.
一种适宜于高速运行的无接触式电磁离合器[J]. 电工技术学报, 2011, 26(12): 68–72.
LI Yong, XING Jingwei, HAN Sufang, et al. A non-contact electromagnetic clutch suitable for high totating speed application[J]. Transactions of China Electrotechnical Societiy, 2011, 26(12): 68–72. (in Chinese) |
| [3] |
赵韩, 李露, 王勇.
电压源励磁的电磁离合器动态特性分析[J]. 农业机械学报, 2008, 39(4): 187–189.
ZHAO Han, LI Lu, WANG Yong. Dynamic characterestic analysisi of votage source electromagnetic clutch[J]. Transactions of the Chinese Society for Agricutural Machinery, 2008, 39(4): 187–189. (in Chinese) |
| [4] | Jaindl M, Kostinger A, Magele C, et al. Optimal design of a disk type magnetorheologic fluid clutch[J]. Elektrotechnik & Informationstechnik, 2009, 124(7): 266–267. |
| [5] |
王淑红, 肖旭亮, 熊光煜.
直流恒力电磁铁特性[J]. 机械工程学报, 2008, 44(2): 244–245.
WANG Shuhong, XIAO Xuliang, XIONG Guangyu. Direct current electromagnets with constant traction characteristic[J]. Chinese Journal of Mechanical Engineering, 2008, 44(2): 244–245. (in Chinese) |
| [6] |
张齐.
基于Ansoft的比例电磁铁电磁力的有限元分析[J]. 沈阳师范大学学报:自然科学版, 2009, 27(3): 306–307.
ZHANG Qi. Finite element analysis of the proportion of electromagnet force based on Ansoft[J]. Journal of Shenyang Normal University:Natural Science Edition, 2009, 27(3): 306–307. (in Chinese) |
| [7] | 赵博, 张洪亮. Ansoft 12在工程电磁场中的应用[M]. 北京: 中国水利水电出版社, 2010. |
| [8] | Hartfield R J, Jenkins R M, Burkhalter J E, et al. Optimizing a solid rocket motor boosted ramjet powered missile using a genetic algorithm[J]. Applied Mathemmatics and Computation, 2006, 181(2): 1720–1726. DOI:10.1016/j.amc.2006.03.028 |
| [9] | Rahideh A, Korakianitis T, Ruiz P, et al. Optimal brushless DC motor design using genetic algorithms[J]. Journal of Magnetism and Magnetic Materials, 2010, 322(22): 3680–3687. DOI:10.1016/j.jmmm.2010.07.025 |
| [10] | Sanz-Garcia A, Pernia-Espinoza A V, Fernández-Martinez R, et al. Combining genetic algorithms and the finite element method to improve steel industrial processes[J]. Journal of Applied Logic, 2012, 10(4): 298–308. DOI:10.1016/j.jal.2012.07.006 |
| [11] |
满军, 丁凡, 李其朋, 等.
圆锥和平面磁极高速电磁铁动态特性对比[J]. 农业机械学报, 20009, 40(3): 298–300.
MAN Jun, DING Fan, LI Qipeng, et al. Comparative researches on high-speed solenoids of conical pole and planar pole[J]. Transactions of the Chinese Society for Agricutural Machinery, 20009, 40(3): 298–300. (in Chinese) |
| [12] | Kerem K, Edward J P, Afzal S. Design consideration for an automotive magnetorheological brake[J]. Mechatronics, 2008, 18(8): 434–447. DOI:10.1016/j.mechatronics.2008.02.003 |
| [13] |
白相林, 李浩昱, 刘文剑.
一种新型电磁离合器[J]. 吉林大学学报:工学版, 2011, 41(3): 684–690.
BAI Xianglin, LI Haoyu, LIU Wenjia. Novel electromagnetic clutch[J]. Journal of Jilin University:Engineering and Technology Edition, 2011, 41(3): 684–690. (in Chinese) |
| [14] | Lim T M, Zhang D S, Yang J J, et al. Design and parameter estimation of hybrid magnetic bearings for blood pump applications[J]. Mechanical System and Signal Processing, 2009, 23(7): 2352–2382. DOI:10.1016/j.ymssp.2009.03.012 |
| [15] | Lim J, Park H, An J, et al. One pneumatic line based inchworm like micro robot for half-inch pipe inspection[J]. Mechatronics, 2008, 18(7): 315–322. DOI:10.1016/j.mechatronics.2008.05.007 |
 2014, Vol. 37
2014, Vol. 37

