滤波减速器[1]因具有大转矩、高刚度、高效率、小体积、大传动比和高可靠性等特点而作为机器人传动关节的主要部件。滤波减速器传动机器人是一个高阶、非线性、强耦合和多变量的非线性控制对象,运转过程中受到各种不确定、非线性、外界扰动等因素影响,它们的存在严重影响机器人控制精度、控制稳定性以及动态响应。国内外对非线性的滤波减速器传动机器人控制研究较少,因而研究其控制方法从而改善系统的动静态性能具有重要的理论研究和工程应用意义。非线性控制方法的发展很快,诸如PID控制[2-3]、计算机力矩控制[4-5]、反演控制[6-7]、自适应控制[8-9]、神经网络控制[10-11]和滑模变结构控制[12-13]等。Seyfferth等[14]提出了柔性关节机器人的非线性谐波传动模型并进行参数辨识,但模型中更多考虑磁滞的可塑性。Chien等[15]针对时变不确定性柔性关节机器人提出鲁棒自适应控制器解决跟踪问题。Li等[16]研究了基于backstepping的直流电机驱动单关节柔性机器手自适应模糊输出反馈控制问题,但未考虑非线性因素。刘金琨[17]针对单连杆柔性关节机器人控制系统设计了backstepping控制方法,但虚拟项多次微分产生所谓“系数膨胀”问题。
自适应反演控制方法将复杂的非线性系统分解成不超过系统阶数的子系统,然后独立设计子系统的Lyapunov函数,在子系统收敛的前提下构建相应的虚拟控制率和自适应率。同时,下一个子系统设计将以上一个子系统的虚拟控制率为基础,如此反复,最终得到实际的虚拟控制率和自适应率。
笔者应用RBF神经网络逼近系统未知的非线性函数,设计自适应RBF反演法控制器,利用Lyapunov理论分析闭环系统的稳定性。仿真结果表明所提控制方案保证了闭环系统的有界性和高精度跟踪性,有效地抑制诸如参数未知、外界扰动等对机器人的影响,具有较强的鲁棒性。
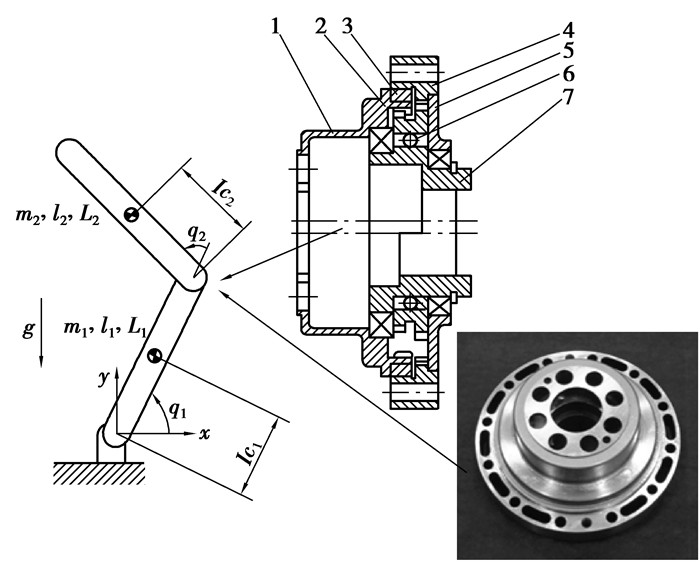
1 系统数学模型机器人主要由滤波减速器、电机和连杆等构成,常用伺服电机已成熟化、标准化和系统化,但减速器因其具有复杂性和特殊性而制约机器人朝高精度、高品质发展。如图 1所示机器人关节部位的滤波减速器由输出齿轮、双联齿轮、滚柱、固定齿轮、轴承座、钢球和偏心轴构成。
|
图 1 滤波减速器传动机器人 1—输出齿轮;2—双联齿轮;3—滚柱;4—固定齿轮;5—轴承座;6—钢球;7—偏心轴 |
对于滤波减速器传动的机器人,在忽略齿隙、死区等因素下,包含电气和机械子系统的滤波减速器传动机器人数学模型描述如下:
| $ {\mathit{\boldsymbol{M}}_{\rm{H}}}\left( q \right)\ddot q + {\mathit{\boldsymbol{C}}_{\rm{H}}}\left( {q,\dot q} \right)\dot {q +} {\mathit{\boldsymbol{G}}_{\rm{H}}}\left( q \right) - {\mathit{\boldsymbol{\tau }}_{{\rm{ed}}}} = \mathit{\boldsymbol{\tau }}, $ | (1) |
| $ {\mathit{\boldsymbol{J}}_m}{{\ddot q}_m} + {\mathit{\boldsymbol{B}}_m}{{\dot q}_m} + {\mathit{\boldsymbol{\tau }}_1} = {\mathit{\boldsymbol{\tau }}_m}, $ | (2) |
| $ {\mathit{\boldsymbol{\tau }}_m} = {\mathit{\boldsymbol{K}}_{\rm{T}}}i, $ | (3) |
| $ \mathit{\boldsymbol{L}}i + \mathit{\boldsymbol{R}}i + {\mathit{\boldsymbol{K}}_{\rm{e}}}{{\dot q}_m} + {\mathit{\boldsymbol{u}}_{{\rm{ed}}}} = \mathit{\boldsymbol{u}}。$ | (4) |
式中:MH为机器人惯量矩阵;CH为机器人哥氏力和离心力矩阵;GH为机器人重力矢量;τed为机器人力矩干扰项;τ为机器人输入力矩;Jm为电机的惯量矩阵;Bm为电机粘滞摩擦系数;τ1为电机负载力矩;τm为电机力矩矢量;KT}为电机转矩常数;ued为有界干扰电压矢量;u为电机电压矢量;i为电机电流向量;q、
电机与机器人之间关系如下:
| $ {\mathit{\boldsymbol{\tau }}_1} = \mathit{\boldsymbol{N\tau }}, $ | (5) |
| $ q = \mathit{\boldsymbol{N}}{q_m}, $ | (6) |
式中N=diag{n1,n2,…,nn}为滤波减速器传动比的对角矩阵。
将式(5) 和(6) 代入式(1)、(2)、(3) 和(4),得
| $ \mathit{\boldsymbol{M}}\left( q \right)\ddot q + \mathit{\boldsymbol{C}}\left( {q,\dot q} \right)\dot q + \mathit{\boldsymbol{G}}\left( q \right) - {\mathit{\boldsymbol{\tau }}_{\rm{e}}} = {\mathit{\boldsymbol{K}}_{\rm{T}}}i, $ | (7) |
| $ \mathit{\boldsymbol{L}}i + \mathit{\boldsymbol{R}}i + {\mathit{\boldsymbol{K}}_{\rm{e}}}\frac{{\dot q}}{\mathit{\boldsymbol{N}}} + {u_{{\rm{ed}}}} = u, $ | (8) |
式中M(q)=NMH+
注1 假设系统参数是未知但有界的,且系统具有以下特性:
1) 惯性矩阵M(q)是正定对称矩阵,且M(q)有界,即存在σo>0,σo∈R,0 < M(q)≤σoI。
2) 惯性矩阵M(q)与哥氏力和离心力矩阵C(q,
两关节滤波减速器传动的机器人动力学各项的具体表达式如下:
| $ {\mathit{\boldsymbol{M}}_{\rm{H}}}\left( q \right) = \\\left[ {\begin{array}{*{20}{c}} {{m_1}l_{{{\rm{c}}_1}}^2 + {I_1} + {m_2}\left( {l_1^2 + l_{{{\rm{c}}_2}}^2 + 2{l_1}{l_{{{\rm{c}}_2}}}\cos {q_2}} \right) + {I_2}}&{{m_2}{l_1}{l_{{{\rm{c}}_2}}}\cos {q_2} + {m_2}l_{{{\rm{c}}_2}}^2 + {I_2}}\\ {{m_2}{l_1}{l_{{{\rm{c}}_2}}}\cos {q_2} + {m_2}l_{{{\rm{c}}_2}}^2 + {I_2}}&{{m_2}l_{{{\rm{c}}_2}}^2 + {I_2}} \end{array}} \right]; $ |
| $ {\mathit{\boldsymbol{C}}_{\rm{H}}}\left( {q,\dot q} \right) = \left[ {\begin{array}{*{20}{c}} { - {m_2}{l_1}{l_{{{\rm{c}}_2}}}\sin {q_2}{{\dot q}_2}}&{ - {m_2}{l_1}{l_{{{\rm{c}}_2}}}\sin {q_2}\left( {{{\dot q}_1} + {{\dot q}_2}} \right)}\\ {{m_2}{l_1}{l_{{{\rm{c}}_2}}}\sin {q_2}{{\dot q}_1}}&0 \end{array}} \right]; $ |
| $ {\mathit{\boldsymbol{G}}_{\rm{H}}}\left( q \right) = \left[ \begin{array}{l} {m_1}g{l_{{{\rm{c}}_1}}}\cos {q_1} + {m_2}g{l_1}\cos {q_1} + {m_2}g{l_{{{\rm{c}}_2}}}\cos \left( {{q_1} + {q_2}} \right)\\ {m_2}g{l_{{{\rm{c}}_2}}}\cos \left( {{q_1} + {q_2}} \right) \end{array} \right]。$ |
定义系统状态变量x1=q,x2=
| $ {{\dot x}_1} = {x_2}, $ | (9) |
| $ {{\dot x}_2} = \frac{1}{M}\left( {{K_{\rm{T}}}{x_3} - \mathit{\boldsymbol{C}}{x_2} - \mathit{\boldsymbol{G}} + {\tau _{\rm{e}}}} \right), $ | (10) |
| $ {{\dot x}_3} = \frac{1}{\mathit{\boldsymbol{L}}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{R}}{x_3} - \frac{1}{\mathit{\boldsymbol{N}}}{\mathit{\boldsymbol{K}}_{\rm{e}}}{x_2} - {u_{{\rm{ed}}}}} \right)。$ | (11) |
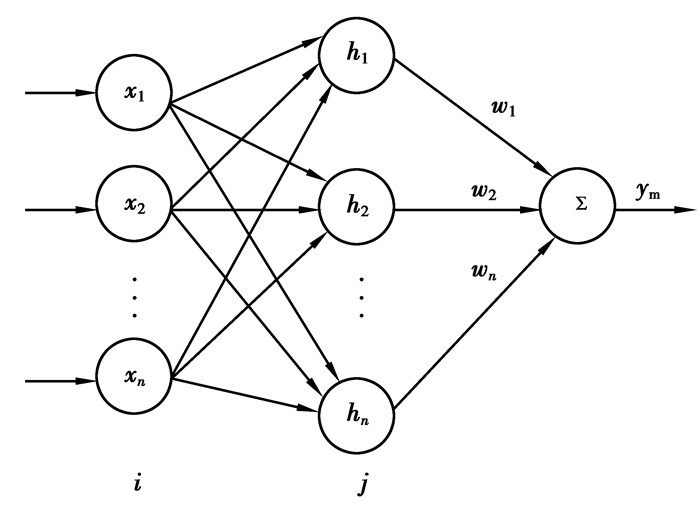
在图 2所示的RBF神经网络结构中,x=[x1,x2,…,xn]T为网络的输入向量,H=[h1,h2,…,hm]T为径向基向量,其中hj为高斯基函数,其表达式为
| $ {h_j} = \exp \left( { - \frac{{\left\| {\mathit{\boldsymbol{x}} - c_j^2} \right\|}}{{2b_j^2}}} \right), $ | (12) |
|
图 2 RBF神经网络结构 |
式中j=1,2,…,m,神经网络第j个节点的中心矢量为cj=[cj1,cj2,…,cjn]。
设神经网络的基宽向量为
| $ \mathit{\boldsymbol{B}} = {\left[ {{b_1},{b_2}, \cdots ,{b_m}} \right]^{\rm{T}}}, $ |
式中bj为节点j的基宽度参数,且为大于零的数。网络的权向量为
| $ \mathit{\boldsymbol{W}} = {\left[ {{\omega _1},{\omega _2}, \cdots ,{\omega _m}} \right]^{\rm{T}}}, $ |
RBF神经网络的输出为
| $ {\mathit{\boldsymbol{y}}_m}\left( t \right) = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{H}} = \sum\limits_{i = 1}^m {{\omega _i}{h_i}} 。$ | (13) |
根据反演法原理[7-10],获得整个闭环系统的实际控制率和自适应率步骤如下。
Step 1
根据给定系统参考信号x1d,定义跟踪误差变量z1=x1-x1d,则
| $ {{\dot z}_1} = {x_2} - {{\dot x}_{1{\rm{d}}}}, $ | (14) |
选取Lyapunov控制函数如下:
| $ {V_1} = \frac{1}{2}z_1^{\rm{T}}{z_1}, $ | (15) |
对V1求导
构造虚拟控制器为
| $ {\alpha _1}\left( {{\mathit{\boldsymbol{Z}}_1}} \right) = - {k_1}{z_1} + {{\dot x}_{1{\rm{d}}}}, $ | (16) |
式中k1>0是控制器参数,Z1=[x1,x1d,
利用式(15)、(16) 可变为
| $ {{\dot V}_1} = - {k_1}z_1^{\rm{T}}{z_1} + z_1^{\rm{T}}{z_2}, $ | (17) |
定义z2=x2-α1。
Step 2
对z2求导得
| $ {{\dot z}_2} = {{\dot x}_2} - {{\dot \alpha }_1} = \frac{1}{\mathit{\boldsymbol{M}}}\left( {{\mathit{\boldsymbol{K}}_{\rm{T}}}{x_3} - \mathit{\boldsymbol{C}}{x_2} - \mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{\tau }}_{\rm{e}}}} \right) - {{\dot \alpha }_1}, $ | (18) |
选取Lyapunov控制函数,得
| $ {V_2} = {V_1} + \frac{1}{2}z_2^{\rm{T}}\mathit{\boldsymbol{M}}{z_2}, $ | (19) |
对V2求导得
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} + {{\dot V}_1} + z_2^{\rm{T}}\mathit{\boldsymbol{M}}{{\dot z}_2} + \frac{1}{2}z_2^{\rm{T}}\mathit{\boldsymbol{\dot M}}{{z}_2} = \\{{\dot V}_1} + z_2^{\rm{T}}\mathit{\boldsymbol{M}}\left[ {\frac{1}{\mathit{\boldsymbol{M}}}\left( {{\mathit{\boldsymbol{K}}_{\rm{T}}}{x_3} - \mathit{\boldsymbol{C}}{x_2} - \mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{\tau }}_{\rm{e}}}} \right) - {{\dot \alpha }_1}} \right] + \frac{1}{2}z_2^{\rm{T}}\mathit{\boldsymbol{\dot M}}{{z}_2} = }\\ {{{\dot V}_1} + z_2^{\rm{T}}\left( {{\mathit{\boldsymbol{K}}_{\rm{T}}}{x_3} - \mathit{\boldsymbol{C}}\left( {{x_2} - {z_2}} \right) - \mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{\tau }}_{\rm{e}}} - \mathit{\boldsymbol{M}}{{\dot \alpha }_1}} \right) = }\\ { - {k_1}z_1^{\rm{T}}{z_1} + z_2^{\rm{T}}\left( {{\mathit{\boldsymbol{K}}_{\rm{T}}}{x_3} - \mathit{\boldsymbol{C}}{\alpha _1} + {z_1} - \mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{\tau }}_{\rm{e}}} - \mathit{\boldsymbol{M}}{{\dot \alpha }_1}} \right).} \end{array} $ | (20) |
注 2 此处假定系统扰动τe是未知,但是其上界为τh>0,即τh>τe>0。
根据Young’s不等式
| $ {{\dot V}_2} \le - {k_1}z_1^{\rm{T}}{z_1} + z_2^{\rm{T}}\left( {{\mathit{\boldsymbol{K}}_{\rm{T}}}{x_3} + {z_1} - \mathit{\boldsymbol{C}}{\alpha _1} - \mathit{\boldsymbol{G}} + \frac{1}{{2{\varepsilon ^2}}}{z_2} - \mathit{\boldsymbol{M}}{{\dot \alpha }_1}} \right) + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2。$ | (21) |
转动惯量M是未知量,选取
构造虚拟控制器
| $ {\alpha _2}\left( {{\mathit{\boldsymbol{Z}}_2}} \right) = \frac{1}{{{\mathit{\boldsymbol{K}}_{\rm{T}}}}}\left( { - {k_2}{z_2} - {z_1} + \mathit{\boldsymbol{C}}{\alpha _1} + \mathit{\boldsymbol{G}} - \frac{1}{{2{\varepsilon ^2}}}{z_2} + \mathit{\boldsymbol{\hat M}}{{\dot \alpha }_1}} \right), $ | (22) |
式中k2>0是控制器设计参数,Z2=[x1,x2,x1d,
定义z3=x3-α2,
| $ 则\ \ \ \ \ \ \ {{\dot V}_2} = \sum\limits_{i = 1}^2 {{k_i}z_i^{\rm{T}}{z_i}} + z_2^{\rm{T}}\left( {{\mathit{\boldsymbol{K}}_{\rm{T}}}{z_3} + \left( {\mathit{\boldsymbol{\hat M}} - \mathit{\boldsymbol{M}}} \right){{\dot \alpha }_1}} \right) + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2。$ | (23) |
Step 3
对z3求导得
| $ {{\dot z}_3} = {{\dot x}_3} - {{\dot \alpha }_2} = \frac{1}{\mathit{\boldsymbol{L}}}\left( {u - \mathit{\boldsymbol{R}}{x_3} - \frac{{{\mathit{\boldsymbol{K}}_{\rm{e}}}}}{\mathit{\boldsymbol{N}}}{x_2} - {u_{{\rm{ed}}}}} \right) - {{\dot \alpha }_2}。$ | (24) |
选取Lyapunov控制函数
| $ {V_3} = {V_2} + \frac{1}{2}z_3^{\rm{T}}{z_3}, $ | (25) |
对V3求导得
| $ \begin{array}{*{20}{c}} {{{\dot V}_3} = {{\dot V}_2} + z_3^{\rm{T}}{{\dot z}_3} = {{\dot V}_2} + z_3^{\rm{T}}\left[ {1/\mathit{\boldsymbol{L}} * \left( {u - \mathit{\boldsymbol{R}}{x_3} - {\mathit{\boldsymbol{K}}_{\rm{e}}}/\mathit{\boldsymbol{N}} * {x_2} - {u_{{\rm{ed}}}}} \right) - {{\dot \alpha }_2}} \right] = }\\ { - \sum\limits_{i = 1}^2 {{k_i}z_i^{\rm{T}}{z_i}} + z_2^{\rm{T}}\left( {\mathit{\boldsymbol{\hat M}} - \mathit{\boldsymbol{M}}} \right){{\dot \alpha }_1} + \frac{{{\varepsilon ^2}}}{2}\tau _{\rm{h}}^2 + z_3^{\rm{T}}\left( {{f_3} + \frac{1}{\mathit{\boldsymbol{L}}}u} \right),} \end{array} $ | (26) |
其中
| $ {{\dot \alpha }_1} = - {\mathit{\boldsymbol{K}}_1}\left( {{x_2} - {{\dot x}_{{\rm{1d}}}}} \right) + {{\ddot x}_{{\rm{1d}}}}, $ | (27) |
| $ {{\dot \alpha }_2} = \sum\limits_{i = 1}^2 {\frac{{\partial {\alpha _2}}}{{\partial {x_i}}}{{\dot x}_i}} + \sum\limits_{i = 1}^2 {\frac{{\partial {\alpha _2}}}{{\partial x_{{\rm{1d}}}^{\left( i \right)}}}x_{{\rm{1d}}}^{\left( {i + 1} \right)}} + \frac{{\partial {\alpha _2}}}{{\partial \mathit{\boldsymbol{\hat M}}}}\mathit{\boldsymbol{\dot {\hat M}}}, $ | (28) |
| $ {f_3}\left( {{\mathit{\boldsymbol{Z}}_3}} \right) = \frac{1}{\mathit{\boldsymbol{L}}}\left( {{\mathit{\boldsymbol{K}}_{\rm{T}}}{z_2} - \mathit{\boldsymbol{L}}{{\dot \alpha }_2} - \mathit{\boldsymbol{R}}{x_3} - \frac{{{\mathit{\boldsymbol{K}}_{\rm{e}}}}}{\mathit{\boldsymbol{N}}}{x_2} - {u_{{\rm{ed}}}}} \right), $ | (29) |
| $ {\mathit{\boldsymbol{Z}}_3} = {\left[ {{x_1},{x_2},{x_3},{x_{{\rm{1d}}}},{{\dot x}_{{\rm{1d}}}},\mathit{\boldsymbol{\hat M}}} \right]^{\rm{T}}}。$ |
f3中既含有
| $ {f_3}\left( {{z_3}} \right) = w_3^{\rm{T}}{s_3}\left( {{z_3}} \right) + {\delta _3}\left( {{z_3}} \right), $ | (30) |
式中δ3表示逼近误差,并满足不等式|δ3|≤ε3。
根据Young’s不等式可知
| $ z_3^{\rm{T}}{f_3}\left( {{z_3}} \right) = z_3^{\rm{T}}\left( {w_3^{\rm{T}}{s_3}\left( {{z_3}} \right) + {\delta _3}\left( {{z_3}} \right) \le \frac{1}{{2{l^2}}}z_3^2{{\left\| {{w_3}} \right\|}^2}s_3^{\rm{T}}{s_3} + \frac{1}{2}{l^2} + \frac{1}{2}z_3^2 + \frac{1}{2}\varepsilon _3^2} \right), $ | (31) |
把式(31) 代入式(26),得
| $ \begin{array}{*{20}{c}} {{{\dot V}_3} \le - \sum\limits_{i = 1}^2 {{k_i}z_i^{\rm{T}}{z_i}} + z_2^{\rm{T}}\left( {\mathit{\boldsymbol{\hat M}} - \mathit{\boldsymbol{M}}} \right){{\dot \alpha }_1} + z_3^{\rm{T}}\left( {\frac{1}{{2{l^2}}}z_T^2{{\left\| {{w_3}} \right\|}^2}s_3^{\rm{T}}{s_3} + \frac{1}{2}{z_3} + \frac{1}{\mathit{\boldsymbol{L}}}u} \right) + }\\ {\frac{1}{2}{l^2} + \frac{1}{2}\varepsilon _3^2 + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2。} \end{array} $ | (32) |
取控制律
| $ u = \mathit{\boldsymbol{L}}\left( { - {k_3}{z_3} - \frac{1}{2}{z_3} - \frac{1}{{2{l^2}}}z_3^{\rm{T}}\hat \theta s_3^{\rm{T}}{s_3}} \right), $ | (33) |
式中
| $ {{\dot V}_3} \le - \sum\limits_{i = 1}^3 {{k_i}z_i^{\rm{T}}{z_i}} + z_2^{\rm{T}}\left( {\mathit{\boldsymbol{\hat M}} - \mathit{\boldsymbol{M}}} \right){{\dot \alpha }_1} + \frac{1}{{2{l^2}}}z_3^{\rm{T}}{z_3}\left( {{{\left\| {{w_3}} \right\|}^2} - \hat \theta } \right)s_3^{\rm{T}}{s_3} + \frac{1}{2}{l^2} + \frac{1}{2}\varepsilon _3^2 + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2。$ | (34) |
定义误差变量
| $ \mathit{\boldsymbol{\tilde M}} = \mathit{\boldsymbol{\hat M}} - \mathit{\boldsymbol{M}}, $ | (35) |
| $ \tilde \theta = \hat \theta - \theta 。$ | (36) |
选取Lyapunov控制函数
| $ V = {V_3} + \frac{1}{{2{r_1}}}{{\mathit{\boldsymbol{\tilde M}}}^2} + \frac{1}{{2{r_2}}}{{\tilde \theta }^2}, $ | (37) |
对V求导,得
| $ \begin{array}{*{20}{c}} {\dot {V =} {{\dot V}_3} + \frac{1}{{{r_1}}}\mathit{\boldsymbol{\tilde M\dot {\hat M} + }}\frac{1}{{{r_2}}}\tilde \theta \dot {\hat \theta} \le - \sum\limits_{i = 1}^3 {{k_i}z_i^{\rm{T}}{z_i}} + z_2^{\rm{T}}\left( {\mathit{\boldsymbol{\hat M}} - \mathit{\boldsymbol{M}}} \right){{\dot \alpha }_1} + }\\ {\frac{1}{{2{l^2}}}z_3^{\rm{T}}{z_3}\left( {{{\left\| {{w_3}} \right\|}^2} - \hat \theta } \right)s_3^{\rm{T}}{s_3} + \frac{1}{2}{l^2} + \frac{1}{2}\varepsilon _3^2 + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2 + \frac{1}{{{r_1}}}\mathit{\boldsymbol{\tilde M\dot {\hat M} + }}\frac{1}{{{r_2}}}\tilde \theta \dot {\hat \theta} \le }\\ { - \sum\limits_{i = 1}^3 {{k_i}z_i^{\rm{T}}{z_i}} + \frac{1}{{{r_1}}}\mathit{\boldsymbol{\tilde M}}\left( {{r_1}z_2^{\rm{T}}{{\dot \alpha }_1} + \mathit{\boldsymbol{\dot {\hat M}}}} \right) + \frac{1}{{{r_2}}}\tilde \theta \left( { - \frac{1}{{2{l^2}}}{r_2}z_3^{\rm{T}}{z_3}s_3^{\rm{T}}{s_3} + \dot {\hat \theta} } \right) + \frac{1}{2}{l^2} + \frac{1}{2}\varepsilon _3^2 + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2。} \end{array} $ | (38) |
选取自适应律如下:
| $ \mathit{\boldsymbol{\dot {\hat M}}} = - {r_1}z_2^{\rm{T}}{{\dot \alpha }_1} - {m_1}\mathit{\boldsymbol{\hat M}}, $ | (39) |
| $ \dot {\hat \theta} = \frac{1}{{2{l^2}}}{r_2}z_3^{\rm{T}}{z_3}s_3^{\rm{T}}{s_3} - {m_2}\hat \theta , $ | (40) |
式中m1和m2为正数。
3 稳定性分析基于以上控制器,将上述自适应律式(39) 和式(40) 代入式(38),相关稳定性分析如下:
| $ \dot V \le - \sum\limits_{i = 1}^3 {{k_i}z_i^{\rm{T}}{z_i}} + \frac{1}{2}{l^2} + \frac{1}{2}\varepsilon _3^2 + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2 - \frac{{{m_1}}}{{{r_1}}}\mathit{\boldsymbol{\tilde M\hat M}} - \frac{{{m_2}}}{{{r_2}}}\tilde \theta \hat \theta , $ | (41) |
从而有
| $ \dot V \le - \sum\limits_{i = 1}^3 {{k_i}z_i^{\rm{T}}{z_i}} - \frac{1}{2}\frac{{{m_1}}}{{{r_1}}}{{\mathit{\boldsymbol{\tilde M}}}^2} - \frac{1}{2}\frac{{{m_2}}}{{{r_2}}}{{\tilde \theta }^2} + \frac{1}{2}{l^2} + \frac{1}{2}\varepsilon _3^2 + \frac{1}{2}{\varepsilon ^2}\tau _{\rm{h}}^2 + \frac{1}{2}\frac{{{m_1}}}{{{r_1}}}{\mathit{\boldsymbol{M}}^2} +\\ \frac{1}{2}\frac{{{m_2}}}{{{r_2}}}{\theta ^2} \le {a_0}v + {b_0}, $ | (42) |
式中
| $ V\left( t \right) \le \left( {{V_0}\left( t \right) - \frac{{{b_0}}}{{{a_0}}}} \right){{\rm{e}}^{ - {a_0}\left( {t - {t_0}} \right)}} + \frac{{{b_0}}}{{{a_0}}} \le {V_0}\left( {{t_0}} \right) + \frac{{{b_0}}}{{{a_0}}},\forall t \ge {t_0}, $ | (43) |
式(43) 说明变量zi(i=1,2,3),
| $ \mathop {\lim }\limits_{t \to \infty } z_1^2 \le \frac{{2{b_0}}}{{{a_0}}}。$ | (44) |
注3 式(44) 明确了位置跟踪误差的上限。从a0和b0的定义知道,在选择合理的参数值ki和mi后,如果a0保持不变,可以选择较大的ri及较小的l和ε,从而保证2b0/a0值较小。
4 系统仿真分析在Matlab R2011b环境下,利用Simulink与S-function构建控制器,并对实际滤波减速器传动机器人进行仿真实验,其主程序如图 3所示。

|
图 3 RBF神经网络反演法主程序 |
滤波减速器传动机器人的参数为
| $ {L_1} = 0.205,{L_2} = 0.21,{L_{c1}} = 0.1025,{L_{c2}} = 0.105, $ |
| $ {m_1} = 3.55,{m_2} = 0.75,{I_1} = 0.04,{I_2} = 0.03, $ |
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {0.3}&0\\ 0&{0.24} \end{array}} \right],\mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {2.8}&0\\ 0&{4.8} \end{array}} \right],\mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {160}&0\\ 0&{160} \end{array}} \right],{\mathit{\boldsymbol{K}}_{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {100}&0\\ 0&{100} \end{array}} \right],{\mathit{\boldsymbol{J}}_m} = \left[ {\begin{array}{*{20}{c}} {8.7}&0\\ 0&{8.47} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{\tau }}_{\rm{e}}} = \left[ {\begin{array}{*{20}{c}} {0.2\cos \left( {{\rm{ \mathsf{ π} }}t/12} \right)}&0\\ 0&{0.2\cos \left( {{\rm{ \mathsf{ π} }}t/12} \right)} \end{array}} \right],{\mathit{\boldsymbol{K}}_{\rm{e}}} = \left[ {\begin{array}{*{20}{c}} {2.42 \times {{10}^{ - 4}}}&0\\ 0&{2.18 \times {{10}^{ - 4}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{B}}_m} = \left[ {\begin{array}{*{20}{c}} {1.3 \times {{10}^{ - 5}}}&0\\ 0&{2 \times {{10}^{ - 5}}} \end{array}} \right]。$ |
选取滤波减速器传动机器人两关节的外界扰动、初始状态以及期望跟踪轨迹如下:
| $ {\mathit{\boldsymbol{\tau }}_{{\rm{ed}}}} = {\left[ {0.2\cos \left( {{\rm{ \mathsf{ π} }}t/12} \right),0.2\cos \left( {{\rm{ \mathsf{ π} }}t/12} \right)} \right]^{\rm{T}}}, $ |
| $ q\left( 0 \right) = {\left[ {0,0} \right]^{\rm{T}}},\dot {q\left( 0 \right) =} {\left[ {0,0} \right]^{\rm{T}}},\ddot q\left( 0 \right) = {\left[ {0,0} \right]^{\rm{T}}}, $ |
| $ {q_{\rm{d}}} = {\left[ {0.1 + 1.4{{\rm{e}}^{ - 50{t^3}}},1.5 - 0.5{{\rm{e}}^{ - 50{t^3}}}} \right]^{\rm{T}}}。$ |
RBF函数中心和宽度极大地影响了自适应神经网络控制器的性能。因此,设置神经网络包含12个节点,中心cj均匀分布在[-1.5,1.5]× [-1.5,1.5] ×[-1.5,1.5]× [0, 3],宽度bj为1,控制器参数为
| $ {k_1} = 28,{k_2} = 25,{k_3} = 27,{r_1} = 0.01,{r_2} = 0.01,{m_1} = 25,{m_2} = 25,l = 10,\varepsilon = 0.04。$ |
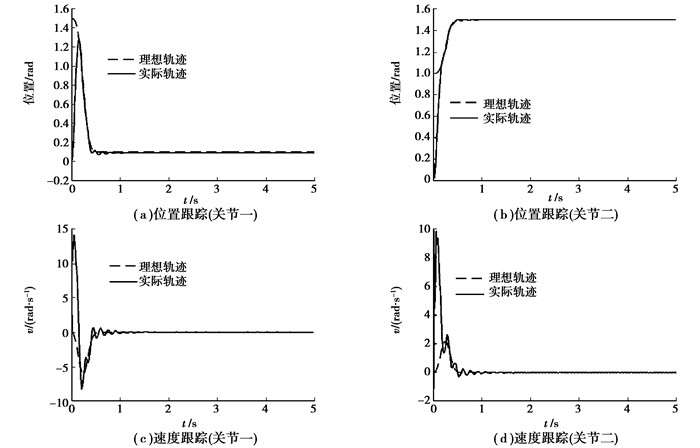
采样时间选取为0.001 s,仿真结果如图 4~5所示,基于RBF神经网络反演控制方法能够克服诸如参数未知、外界扰动等,确保系统1 s以内成功跟踪到给定轨迹信号,且跟踪稳态误差基本上处于±0.003内,实现了高精度控制,同时也验证了所有状态信号全局一致最终有界。
|
图 4 滤波减速器传动机器人的位置与速度跟踪 |
|
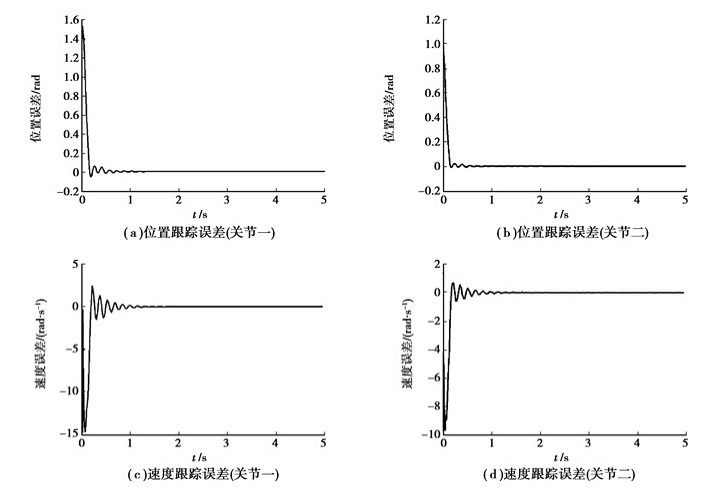
图 5 滤波减速器传动机器人的位置与速度跟踪误差 |
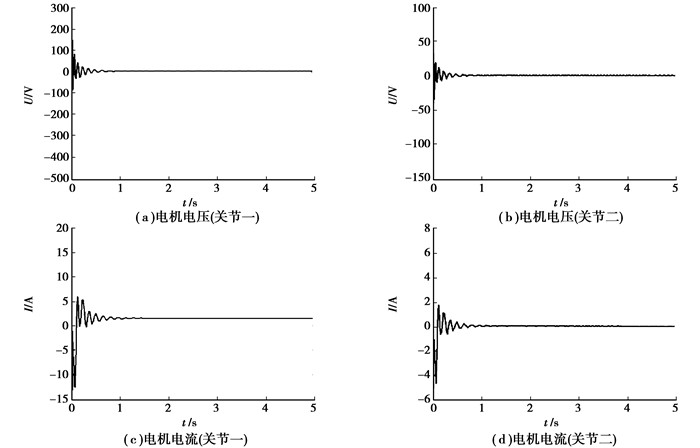
从图 6控制输入电压与电流曲线可知,为加快系统的收敛速度,虽然控制输入在初期需要的能量较大,但随后迅速趋于平衡状态,抖动减小,光滑有界,实现滤波减速器传动机器人连续平稳控制。
|
图 6 滤波减速器传动机器人的电机电压与电流 |
笔者以具有参数未知、外界扰动、强耦合和非线性等特性的滤波减速器传动机器人为研究对象,建立系统数学模型,提出滤波减速器传动机器人的自适应RBF反演控制方法,克服相关文献中经典backstepping控制方法“计算膨胀”的问题,同时采用Lyapunov理论论证误差状态变量快速收敛到原点附近的一个充分小的领域内。仿真结果表明所提控制方法具有较高的跟踪精度和较强的鲁棒性。减速器传动存在柔性变形、死区、时滞、摩擦及传动误差等非线性因素的影响,它们的存在将严重影响系统控制精度、稳定性以及动态响应,而这些将在后续研究工作中得到补充与完善。
| [1] |
王家序, 秦德成, 张林川, 等.
滤波减速器轮齿表面瞬态微观弹流润滑模型[J]. 四川大学学报:工程科学版, 2013, 45(1): 202–207.
WANG Jiaxu, QIN Decheng, ZHANG Linchuan, et al. Transient thermal micro-elastohydrodynamic lubrication model of filtering reducer[J]. Journal of Sichuan University:Engineering Science Edition, 2013, 45(1): 202–207. (in Chinese) |
| [2] | Karasakal O, Guzelkaya M, Eksin I, et al. An error-based on-line rule weight adjustment method for fuzzy PID controllers[J]. Expert Systems with Applications, 2011, 38(8): 10124–10132. DOI:10.1016/j.eswa.2011.02.070 |
| [3] |
李绍铭, 刘寅虎.
基于改进型RBF神经网络多变量系统的PID控制[J]. 重庆大学学报:自然科学版, 2007, 30(2): 53–57.
LI Shaoming, LIU Yinghu. PID control for multivariable system based on ameliorative RBF neural networks[J]. Journal of Chongqing University:Natural Science Edition, 2007, 30(2): 53–57. (in Chinese) |
| [4] | Shang W W, Cong S. Nonlinear computed torque control for a high-speed planar parallel manipulator[J]. Mechatronics, 2009, 19(6): 987–992. DOI:10.1016/j.mechatronics.2009.04.002 |
| [5] | Arnanz R, Miguel L J, Peran J R, et al. A modified direct torque control with fault tolerance[J]. Control Engineering Practice, 2011, 19(9): 1056–1065. DOI:10.1016/j.conengprac.2011.05.007 |
| [6] | Trabelsi R, Khedher A, Mimouni M F, et al. Backstepping control for an induction motor using an adaptive sliding rotor-flux observer[J]. Electric Power Systems Research, 2012, 93: 1–15. DOI:10.1016/j.epsr.2012.06.004 |
| [7] | Fang F, Wei L. Backstepping-based nonlinear adaptive control for coal-fired utility boiler-turbine units[J]. Applied Energy, 2011, 88(3): 814–824. DOI:10.1016/j.apenergy.2010.09.003 |
| [8] | Zhu Q, Zhang T P, Fei S M. Adaptive tracking control for input delayed MIMO nonlinear systems[J]. Neurocomputing, 2010, 74(1/2/3): 472–480. |
| [9] | Wang W Y, Chien Y H, Leu Y G, et al. Adaptive T-S fuzzy neural modeling and control for general MIMO unknown nonaffine nonlinear systems using projection update laws[J]. Automatica, 2010, 46(5): 852–863. DOI:10.1016/j.automatica.2010.02.024 |
| [10] | Al-duwaish H N, Al-hamouz Z M. A neural network based adaptive sliding mode controller:Application to a power system stabilizer[J]. Energy Conversion and Management, 2011, 52(2): 1533–1538. DOI:10.1016/j.enconman.2010.06.060 |
| [11] | Leng G, Prasad G, Mcginnity T M. An on-line algorithm for creating self-organizing fuzzy neural networks[J]. Neural Networks, 2004, 17(10): 1477–1493. DOI:10.1016/j.neunet.2004.07.009 |
| [12] | Nekoukar V, Erfanian A. Adaptive fuzzy terminal sliding mode control for a class of MIMO uncertain nonlinear systems[J]. Fuzzy Sets and Systems, 2011, 179(1): 34–49. DOI:10.1016/j.fss.2011.05.009 |
| [13] |
胡雪松, 孙才新, 廖勇, 等.
永磁同步风力发电机转矩动态滑模控制器设计[J]. 重庆大学学报, 2011, 34(7): 57–62.
HU Xuesong, SUN Caixin, LIAO Yong, et al. The design of torque dynamic sliding mode controller in permanent magnet synchronous generator for wind turbine[J]. Journal of Chongqing University, 2011, 34(7): 57–62. DOI:10.11835/j.issn.1000-582X.2011.07.010 (in Chinese) |
| [14] | Seyfferth W, Maghzal A J, Angeles J.Nonlinear modeling and parameter identification of harmonic drive robotic transmissions[C]//Proceedings of IEEE International Conference on Robotics and Automation, May 21-27, 1995, Nagoya.Piscataway:IEEE Press, 1995, 3:3027-3032. |
| [15] | Chien M C, Huang A C. Adaptive control for flexible-joint electrically driven robot with time-varying uncertainties[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 1032–1038. DOI:10.1109/TIE.2007.893054 |
| [16] | Li Y M, Tong S C, Li T S. Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via backstepping[J]. Nonlinear Analysis:Real World Applications, 2013, 14(1): 483–494. DOI:10.1016/j.nonrwa.2012.07.010 |
| [17] | 刘金琨. 机器人控制系统的设计与Matlab仿真[M]. 北京: 清华大学岀版社, 2008. |
 2014, Vol. 37
2014, Vol. 37



