2. 中国石油东方地球物理公司油藏地球物理研究中心, 河北 涿州 072751;
3. 中国工程院, 北京 100088
2. Research Centre of Reservoir Geophysics, BGP Inc. of CNPC, Zhuozhou, Hebei 072751, China;
3. Chinese Academy of Engineering, Beijing 100088, China
蒸汽驱是稠油油藏提高采收率的一种重要方法,也是目前稠油开采的主要技术之一[1-2]。蒸汽驱过程中,蒸汽即是油层驱替介质又是传热介质,但只有部分热量加热油层,另一部分经顶底盖层散失到地层中,降低了地层的热效率[3-4]。热量的散失除与注汽参数相关外,还受蒸汽超覆的影响[5-8]。蒸汽超覆使蒸汽易于在油层顶部聚集,导致顶底盖层总散热面积增加,加剧了热量的散失。目前评价地层热效率的方法主要有威尔曼(Willman)法和马克斯兰根海姆(Marx-Langenheim)法[9-11],这两种方法都是基于活塞式驱替模型,没有考虑蒸汽超覆现象,计算出的地层热效率偏高,不利于蒸汽驱注采参数的调整及接替开发方式转驱时机的确定。笔者基于前人的研究,在对不同蒸汽前缘蒸汽超覆程度进行定量评价的基础上,推导出了考虑蒸汽超覆的稠油蒸汽驱地层热效率计算模型,并利用拉普拉斯变换及Stehfest数值反演方法进行求解。
1 蒸汽驱热散失特征油层热量的传递分两个部分,一是流体的流动引起热量的传递即对流传热;二是油层中高温部位向低温部位的传热即热传导[11-12]。流体渗流速度较大时,对流传热是主要的传热方式;流体渗流速度较小时,热传导成为主要的传热方式。稠油油层渗透率普遍较大,储层导流能力较强,对流传热占主导地位,如图 1所示。而顶底盖层渗透率低,储层导流能力弱,热传导占主导地位。辽河油田某稠油区块测得地层粉砂质泥岩热导率为1.014 W/(m·K),灰色泥岩为1.007 W/(m·K),油砂热导率为0.221 W/(m·K),因此顶底盖层热传导能力较强,热散失不容忽略。油层热量的散失不仅受导率的影响,还与顶底盖层散热面积相联系。顶底盖层散热面积越大,热量散失越严重。随着蒸汽的不断注入,蒸汽前缘不断扩大,油层热损失面积及热散失增加[13-17]。另一方面,由于稠油油藏多为高孔高渗储层,汽液密度差异大、重力分异强、蒸汽超覆严重,导致散热面积进一步增加,加剧了油层热量的散失。
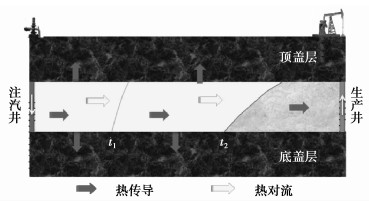
|
图 1 储层热量传递示意图 |
假设条件:1)储层均质,忽略裂缝的影响;2)顶底盖层的导热系数相同,油层及围岩中水平方向热传导为零;3)流体饱和度及油层物性不随温度变化;4)注汽速度及温度为常数,蒸汽腔尚未突破到生产井底;5)油层中蒸汽带和热水带的温度均等于蒸汽温度;6)加热面积是以注汽井为中心的圆形;7)注采压力梯度局限于井网内部生产井与注汽井的作用,忽略井网外部井的影响。
计算步骤:1)分析蒸汽受力及渗流速度,获得不同蒸汽前缘蒸汽超覆程度;2)将油层划分为N个小层,结合各小层蒸汽超覆程度,获得各小层加热热量;3)根据热平衡原理及瞬时热平衡原理获得各小层热平衡方程;4)利用拉普拉斯变换及Stehfest数值反演得到各小层加热面积;5)通过加热面积求得加热带体积的变化,从而获得地层热效率的变化,如图 2所示。
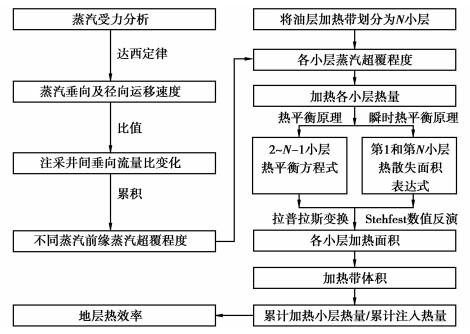
|
图 2 考虑蒸汽超覆地层热效率计算的基本步骤 |
油层多孔介质中,注入蒸汽主要受3种力的影响[18-20]:a.汽液密度差异产生的浮力;b.界面张力产生的毛细管力;c.压力梯度的作用。根据势的叠加原理,距注汽井不同位置处压力梯度的分布为
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}r}} = \frac{{Q\mu }}{{2{\rm{ \mathsf{ π} }}Kh}} \cdot \frac{1}{r} + \sum\limits_{n = 1}^8 {\frac{{{Q_n}\mu }}{{2{\rm{ \mathsf{ π} }}Kh}} \cdot \frac{1}{{{r_n}}}} , $ | (1) |
式中:Q为蒸汽注入速度,m3/d;Qn为第n口生产井产量,m3/d;r为任意点到注汽井的距离,m;h为油层厚度,m;rn为r点对应位置到生产井n的距离,m;K为渗透率,μm2;dp/dr为r处的压力梯度,hPa/m;μ为流体黏度,mPa·s。
单位体积蒸汽所受的浮力可近似看作是恒定的,垂直油层向上[18-20],
| $ {F_{\rm{b}}} = \left( {{\rho _{\rm{o}}} - {\rho _{\rm{g}}}} \right) \cdot g, $ | (2) |
式中:ρg水蒸汽的密度,kg/m3;ρo为油的密度,kg/m3;g为重力加速度,m/s2。
毛细管力存在于任何方向放置的毛细管中。在水湿条件下,毛管力是蒸汽运移的动力,为正值;在油湿条件下,毛细管力阻碍蒸汽的运移,为负值。毛细管力与蒸汽运移同向或反向。
| $ {F_i} = 2 \times {10^{ - 5}}\sigma \cos \theta /{r_{\rm{p}}}, $ | (3) |
式中:θ为接触角,(°);rp为孔隙半径,mm;σ为界面张力,mN/m。
根据达西定律,注入蒸汽在浮力及毛管力的共同作用下,井网内任意点处垂向瞬时渗流速度
| $ {v_{{\rm{gup}}}} = \frac{{{K_{{\rm{up}}}}}}{{{\mu _{\rm{g}}}}}\left( {{F_{\rm{b}}} \pm {F_i}} \right). $ | (4) |
径向瞬时渗流速度
| $ {v_{{\rm{gh}}}} = \frac{{{K_{\rm{h}}}}}{{{\mu _{\rm{g}}}}}\left( {\frac{{{\rm{d}}p}}{{{\rm{d}}x}} \pm {F_i}} \right), $ | (5) |
式中:Kup为垂向渗透率,μm2;μg为黏度,mPa·s;Kh为水平方向渗透率,μm2。
两个渗流速度的比值F为
| $ F = \frac{{{v_{{\rm{gup}}}}}}{{{v_{{\rm{gh}}}}}} = \frac{{{K_{{\rm{up}}}}\left( {{F_{\rm{b}}} \pm {F_i}} \right)}}{{{K_{\rm{h}}}\left( {\frac{{{\rm{d}}p}}{{{\rm{d}}x}} \pm {F_i}} \right)}}。$ | (6) |
按这个比例系数劈分水平方向渗流的蒸汽量和垂直方向运移的蒸汽量,则在油湿条件下,通过蒸汽超覆,运移到油层上部蒸汽的百分比f为
| $ f = \frac{{{v_{{\rm{gup}}}}}}{{{v_{{\rm{gup}}}} + {v_{{\rm{gh}}}}}} = \frac{{{K_{{\rm{up}}}}\left( {{F_{\rm{b}}} - {F_i}} \right)}}{{{k_{{\rm{up}}}}\left( {{F_{\rm{b}}} - {F_i}} \right) + {k_{\rm{h}}}\left( {\frac{{{\rm{d}}p}}{{{\rm{d}}x}} - {F_i}} \right)}}。$ | (7) |
根据式(7),可计算出从注汽井到生产井垂向流量比f的变化(见图 4)。蒸汽超覆程度定义为累计运移到垂向上的蒸汽量与累计注入蒸汽量的比值[18-20],用I表示。将注采井间距离L划分为m(m>2)小块,任一小块大小为dr(dr可趋于无限小,dr越小计算精度越高),距离注汽井距离为ri(i取1,2,…,m)。当蒸汽前缘运移到注采井间第i块(1 < i < m)时,此时的蒸汽超覆程度Ii为第i块蒸汽超覆量和第i-1块的蒸汽超覆程度之和。i等于1时,I1等于f1。
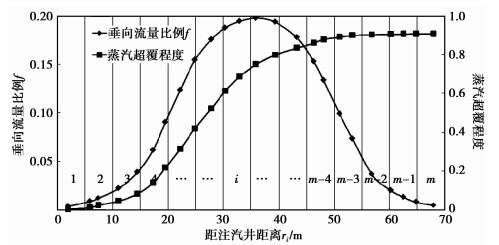
|
图 4 垂向流量比及蒸汽超覆程度曲线 |
| $ {I_i} = \left( {1 - {I_{i - 1}}} \right){f_i} + {I_{i - 1}} = f\left( {{r_i}} \right)。$ | (8) |
根据式(8),可迭代计算出不同蒸汽前缘的蒸汽超覆程度,获得超覆程度Ii与蒸汽腔扩展半径ri的关系图版(见图 4)。Ii数值介于0~1之间,数值越接近于1,蒸汽超覆程度越严重。
2.2 油层加热带体积计算根据油层厚度将油藏划分为N个小层,每个小层厚度为h/N,注入蒸汽量为Q/N。如图 3所示,第1小层与底盖层接触,第N小层与顶盖层接触,小层内蒸汽超覆引起的差异性忽略不计。
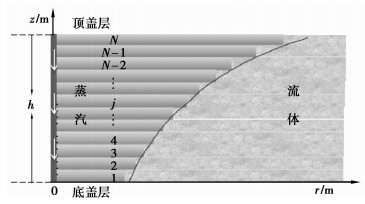
|
图 3 蒸汽腔示意图 |
1) 任取一小层j(1 < j < N),在注汽时间t时,小层加热面积为Aj(t),加热半径rj等于(Aj(t)/π)0.5,小层注热速率qs为[10]
| $ {q_{\rm{s}}} = \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}, $ | (9) |
式中:qs为小层注热速率,kJ/d;Xs井底蒸汽干度,小数;Lv为蒸汽的汽化潜热,kJ/kg;Aj(t)为第j小层加热面积,m2;rj为第j小层加热半径,m。
累计注入热量为
| $ \int_0^t {{q_{\rm{s}}} \cdot {\rm{d}}t} = \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t. $ | (10) |
根据假设条件,由式(8)可得对应加热半径rj下小层的蒸汽超覆程度Ij。在时间t内,由于蒸汽超覆影响流入上部小层的累计热量为Wj,
| $ {W_j} = \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_j}. $ | (11) |
由于蒸汽超覆影响下部小层流入第j层的累计热量为Wj-1,
| $ {W_{j - 1}} = \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_{j - 1}}, $ | (12) |
式中Ij-1为第j-1小层蒸汽超覆程度。
在时间t内加热油层的热量为U,
| $ U = \frac{{{A_j}\left( t \right)hM\Delta T}}{N}, $ | (13) |
| $ M = \varphi \left( {{\rho _{\rm{o}}}{S_{\rm{o}}}{C_{\rm{o}}} + {\rho _{\rm{w}}}{S_{\rm{w}}}{C_{\rm{w}}}} \right) + \left( {1 - \varphi } \right){\left( {\rho C} \right)_{\rm{R}}}, $ | (14) |
式中:M为油层热容,kJ/(m3·℃);ΔT等于Ts减去Tr,蒸汽温度与油层温度之差,℃;Co,Cw为油水的热焓,kJ/kg;(ρC)R为地层岩石的热熔,kJ/(m·℃);φ为油层孔隙度,小数。
根据热平衡原理:注入j层总蒸汽热量-j层蒸汽超覆累计热量+(j-1)层蒸汽超覆累计热量=加热j油层热量,即
| $ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t - \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_j} + \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_{j - 1}} = \frac{{{A_j}\left( t \right)hM\Delta T}}{N}. $ | (15) |
j依次取2到N-1,可得N-2个等式
| $ \left\{ \begin{array}{l} \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t - \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_2} + \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_1} = \frac{{{A_2}\left( t \right)hM\Delta T}}{N}\\ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t - \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_3} + \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_2} = \frac{{{A_3}\left( t \right)hM\Delta T}}{N}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t - \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_j} + \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_{j - 1}} = \frac{{{A_j}\left( t \right)hM\Delta T}}{N}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t - \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_{\left( {N - 2} \right)}} + \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_{\left( {N - 3} \right)}} = \frac{{{A_{\left( {N - 2} \right)}}\left( t \right)hM\Delta T}}{N}\\ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t - \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_{\left( {N - 1} \right)}} + \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}}t \times {I_{\left( {N - 2} \right)}} = \frac{{{A_{\left( {N - 1} \right)}}\left( t \right)hM\Delta T}}{N} \end{array} \right.。$ | (16) |
2) j等于1时,小层为第1小层(底层),与底盖层相互接触。在注汽时间t时,小层加热面积为A1(t)。该小层内,注入蒸汽热量用于3个方面:蒸汽超覆影响流入上部小层热量、向底层的热损失量和加热油层热量。由于向底层的热损失量与加热面积A1(t)相关,而A1(t)随时间变化,累计热损失量不易求解。为便于计算,采取瞬时热平衡原理,即t时刻热能的注入速率等于蒸汽超覆热流速率、底盖层热能损失速率和油层中热能的增长速率之和。
根据油层注蒸汽传热机理,马克斯兰根海姆提出单位面积瞬时热损失为[9]
| $ {q_1} = \frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt {{\rm{ \mathsf{ π} }}Dt} }}, $ | (17) |
式中:ql为油层到顶底盖层的瞬时热损失,kJ/(m2·d);kob为上下盖层的导热系数,kJ/(d·m·℃);D为上下盖层的散热系数,等于kob/Mob;Mob为上下盖层的热容,kJ/(m3·℃)。
底盖层的热散失面积为A1(t),则底盖层的瞬时热损失速率Q1L为
| $ {Q_{1{\rm{L}}}} = \int {{A_1}{{\left( t \right)}_0}{q_1}{\rm{d}}A} = \int {{A_1}{{\left( t \right)}_0}\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt {{\rm{ \mathsf{ π} }}Dt} }}{\rm{d}}A} . $ | (18) |
在时间τ(τ < t),相应的单元面积d A1(t)的热损失为[10]
| $ \frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt {{\rm{ \mathsf{ π} }}D\left( {t - \tau } \right)} }}. $ | (19) |
而
| $ {\rm{d}}{A_1}\left( t \right) = \frac{{{\rm{d}}{A_1}\left( t \right)}}{{{\rm{d}}\tau }} \cdot {\rm{d}}\tau . $ | (20) |
将式(19)、式(20)代入式(18)可得底层的热损失速率
| $ {Q_{1{\rm{L}}}} = \int_0^t {\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt {{\rm{ \mathsf{ π} }}D\left( {t - \tau } \right)} }}\frac{{{\rm{d}}{A_1}\left( t \right)}}{{{\rm{d}}\tau }}{\rm{d}}\tau } . $ | (21) |
在t时刻油层中热能的增长速率为
| $ {Q_{{\rm{o}}1}} = M \cdot \frac{h}{N} \cdot \Delta T \cdot \frac{{{\rm{d}}{A_1}\left( t \right)}}{{{\rm{d}}\tau }}. $ | (22) |
在t时刻由于蒸汽超覆影响流入上部小层的热流速率为
| $ {Q_{{\rm{f1}}}} = {X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}{A_1}\left( t \right)}}{{{\mu _{\rm{g}}}}}\left( {{F_{\rm{b}}} - {F_i}} \right). $ | (23) |
根据瞬时热平衡原理
| $ {q_{\rm{s}}} = {Q_{{\rm{1L}}}} + {Q_{{\rm{o}}1}} + {Q_{{\rm{f1}}}}. $ | (24) |
则
| $ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}} = \int_0^t {\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt {{\rm{ \mathsf{ π} }}D\left( {t - \tau } \right)} }}\frac{{{\rm{d}}{A_1}\left( t \right)}}{{{\rm{d}}\tau }}{\rm{d}}\tau } + \frac{{Mh\Delta T}}{N}\frac{{{\rm{d}}{A_1}\left( t \right)}}{{{\rm{d}}t }} + {X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}{A_1}\left( t \right)}}{{{\mu _{\rm{g}}}}}\left( {{F_{\rm{b}}} - {F_i}} \right). $ | (25) |
利用Laplace变换,式(25)化为
| $ F\left( S \right) = \frac{{Q{\rho _{\rm{g}}} \cdot {X_{\rm{s}}}{L_{\rm{v}}}}}{{N\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt D }}{S^{\frac{3}{2}}} + Mh\Delta T{S^2} + N{X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}\left( {{F_{\rm{b}}} - {F_i}} \right)}}{{{\mu _{\rm{g}}}}}S}}. $ | (26) |
因此,底层加热面积A1(t)的表达式为
| $ {A_1}\left( t \right) = {L^{ - 1}}\left( {F\left( S \right)} \right) = {L^{ - 1}}\left[ {\frac{{Q{\rho _{\rm{g}}} \cdot {X_{\rm{s}}}{L_{\rm{v}}}}}{{N\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt D }}{S^{\frac{3}{2}}} + Mh\Delta T{S^2} + N{X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}\left( {{F_{\rm{b}}} - {F_i}} \right)}}{{{\mu _{\rm{g}}}}}S}}} \right]. $ | (27) |
加热半径r1(t)的表达式为
| $ {r_1}\left( t \right) = \sqrt {\frac{{{A_1}\left( t \right)}}{{\rm{ \mathsf{ π} }}}} = \sqrt {\frac{{{L^{ - 1}}\left( {\frac{{Q{\rho _{\rm{g}}}{X_{\rm{s}}}{L_{\rm{v}}}}}{{N\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt D }}{S^{\frac{3}{2}}} + Mh\Delta T{S^2} + N{X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}\left( {{F_{\rm{b}}} - {F_i}} \right)}}{{{\mu _{\rm{g}}}}}S}}} \right)}}{{\rm{ \mathsf{ π} }}}} . $ | (28) |
3) j等于N时,小层为第N小层(顶层),与顶盖层相互接触。第(N-1)层蒸汽超覆流入热量及注入热量主要用于顶层的热损失和加热油层。根据瞬时热平衡原理,在t时刻,注热速率加(N-1)层蒸汽超覆热流速率等于顶层热损失速率及油层中热能的增长速率,即
| $ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}} + {X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}{A_{\left( {N - 1} \right)}}\left( t \right)}}{{{\mu _{\rm{g}}}}}\left( {{F_{\rm{b}}} - {F_i}} \right) = \int_0^t {\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt {{\rm{ \mathsf{ π} }}D\left( {t - \tau } \right)} }}\frac{{{\rm{d}}{A_N}\left( t \right)}}{{{\rm{d}}\tau }}{\rm{d}}\tau } + \frac{{Mh\Delta T}}{N}\frac{{{\rm{d}}{A_N}\left( t \right)}}{{{\rm{d}}t}}. $ | (29) |
由于第N小层蒸汽加热面积AN(t)与第N-1小层蒸汽加热面积A(N-1)(t)相近,上式可化为
| $ \frac{{Q{\rho _{\rm{g}}}}}{N}{X_{\rm{s}}}{L_{\rm{v}}} + {X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}{A_{\left( N \right)}}\left( t \right)}}{{{\mu _{\rm{g}}}}}\left( {{F_{\rm{b}}} - {F_i}} \right) = \int_0^t {\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt {{\rm{ \mathsf{ π} }}D\left( {t - \tau } \right)} }}\frac{{{\rm{d}}{A_N}\left( t \right)}}{{{\rm{d}}\tau }}{\rm{d}}\tau } + \frac{{Mh\Delta T}}{N}\frac{{{\rm{d}}{A_N}\left( t \right)}}{{{\rm{d}}t}}. $ | (30) |
根据Laplace变换,顶层加热面积AN的表达式为
| $ {A_{\left( N \right)}}\left( t \right) = {L^{ - 1}}\left[ {F\left( S \right)} \right] = {L^{ - 1}} \cdot \left[ {\frac{{Q{\rho _{\rm{g}}} \cdot {X_{\rm{s}}}{L_{\rm{v}}}}}{{N\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt D }}{S^{\frac{3}{2}}} + Mh\Delta T{S^2} - N{X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}\left( {{F_{\rm{b}}} - {F_i}} \right)}}{{{\mu _{\rm{g}}}}}S}}} \right]. $ | (31) |
加热半径rN(t)的表达式为
| $ {r_N}\left( t \right) = \sqrt {{L^{ - 1}}\left[ {\frac{{Q{\rho _{\rm{g}}} \cdot {X_{\rm{s}}}{L_{\rm{v}}}}}{{\left( {N\frac{{{k_{{\rm{ob}}}}\Delta T}}{{\sqrt D }}{S^{\frac{3}{2}}} + Mh\Delta T{S^2} - N{X_{\rm{s}}}{L_{\rm{v}}}\frac{{{K_{{\rm{up}}}}{\rho _{\rm{g}}}\left( {{F_{\rm{b}}} - {F_i}} \right)}}{{{\mu _{\rm{g}}}}}S} \right.}}} \right]{{\rm{ \mathsf{ π} }}^{ - 1}}} . $ | (32) |
式(16)、式(27)、式(31)共有N个方程N个未知数,取任一时间t,对求得的拉氏空间下加热面积进行Stehfest数值反演,获得对应A1(t),AN(t)及加热半径r1(t),rN(t)的大小。根据r1(t)数值大小查找式(8)获得的超覆程度与蒸汽腔扩展半径关系图版(图 4)得到对应I1大小。将I1代入式(16)中第2小层热平衡方程,获得第2小层A2(t)与I2的关系式,结合超覆程度与蒸汽腔扩展半径关系图版求得A2(t)大小(图 4)。依次可计算出各小层的加热面积Aj(t)。因此,油层加热带的体积为
| $ V = \sum\limits_{j = 1}^N {\frac{{{A_j}\left( t \right)h}}{N}} . $ | (33) |
小层层数N是根据油藏厚度划分的,在油藏厚度一定的条件下,层数N越大,小层厚度越薄,蒸汽超覆影响越接近实际情况。然而若小层厚度过薄,小层边界效应明显,层与层之间干扰作用强,油藏顶底层散热量偏离实际情况,导致热效率计算不精确。通过大量理论计算及数值模拟验证,小层厚度为2~3 m时,已有足够的精确性。
2.3 考虑蒸汽超覆热效率计算如图 1所示,注蒸汽过程中,注入热量主要用于两个方面,一是通过第1和第N小层与顶底盖层的接触面散失到地层中,造成注入热量的热损失效应;另一部分热量用于加热油层,是蒸汽驱的主要目的。注蒸汽时间t时,累计注入油藏热量为
| $ \int_0^t {{q_s} \cdot N \cdot {\rm{d}}t} = {X_{\rm{s}}}{L_{\rm{v}}}Q{\rho _{\rm{g}}}t. $ | (34) |
加热油层的总热量为各加热小层累计热量之和
| $ V \cdot M \cdot \Delta T = \sum\limits_{j = 1}^N {\frac{{{A_j}\left( t \right)hM\Delta T}}{N}} . $ | (35) |
油藏热效率为加热油层的总热量占累计注入热量的百分率
| $ \eta r = \frac{{V \cdot M \cdot \Delta T}}{{{X_{\rm{s}}}{L_{\rm{v}}}Q{\rho _{\rm{g}}}t}} = \frac{{\sum\limits_{j = 1}^N {\frac{{{A_j}\left( t \right)hM\Delta T}}{N}} }}{{{X_{\rm{s}}}{L_{\rm{v}}}Q{\rho _{\rm{g}}}t}}. $ | (36) |
某稠油区块油藏深度800~1 200 m,油层厚度26 m,原始地层压力9.5 MPa,原始地层温度50 ℃,孔隙度27.6%,渗透率0.5~4 μm2。在地层温度下脱气原油粘度420 mPa·s,原油密度962 kg/m3,原油体积系数1.06,初始含油饱和度65%。岩石孔隙压缩系数1.3×10-4 MPa-1,油层岩石热容(ρCp)R为2 860 kJ/(m3· ℃),油层岩石导热系数为256 kJ/(d·m· ℃),顶底层岩石热容(ρCp)ob为2 730 kJ/(m3· ℃),顶底层岩石导热系数kob为274 kJ/(d·m· ℃)。油藏进行注蒸汽开采,采用反九点注采井网,边井距注汽井距离70 m,角井距注汽井距离约100 m,注汽速度为160 m3/d,注汽温度为320 ℃,井底蒸汽干度50%~70%。
3.1 蒸汽超覆程度评价根据式(7)、式(8),得垂向流量比f的变化及不同蒸汽前缘蒸汽超覆程度。如图 4所示,在注汽井附近,蒸汽主要沿径向运移,蒸汽超覆程度小,超覆导致的影响可以忽略;在远离注汽井的中间区域,蒸汽超覆程度急剧增加。在生产井附近,蒸汽超覆程度增加缓慢,但超覆程度很大。蒸汽超覆程度随着蒸汽前缘的推进而越来越严重。
3.2 油层加热带体积的变化油藏厚度为26 m,取小层层数N为10,单层厚度为2.6 m。根据式(16)~(32),取不同时间t,经Stehfest数值反演及迭代计算得不同注汽时间加热带的变化曲线,如图 5所示。随着注汽时间的增加,受蒸汽超覆的影响,蒸汽的垂向波及效率逐渐降低。在注汽早期阶段,蒸汽超覆影响不明显,蒸汽腔均匀扩展。在注汽中后期阶段,蒸汽垂向波及差异增大,油藏底部蒸汽波及少,蒸汽沿油层顶部驱替作用明显。
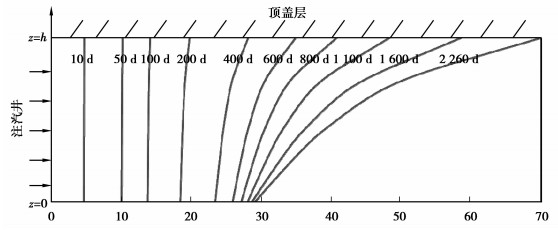
|
图 5 图不同注汽时间蒸汽腔前缘 |
根据式(36),油层热效率计算结果如图 6所示,并与Willman(不考虑蒸汽超覆)计算结果进行比较。蒸汽驱早期阶段,蒸汽超覆程度较弱,超覆导致的影响不明显,考虑蒸汽超覆与不考虑蒸汽超覆热效率基本相近;蒸汽驱中后期阶段,随着蒸汽超覆程度的增加,油藏热效率明显低于不考虑蒸汽超覆热效率。
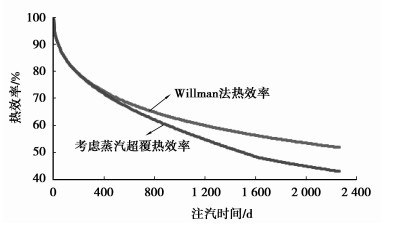
|
图 6 考虑蒸汽超覆与威尔曼法热效率曲线 |
1) 基于热力学平衡原理和流体渗流方程,建立了考虑蒸汽超覆的储层热效率评价模型。模型对蒸汽运移规律的数学描述及热效率的评价能够吻合物理及数值模拟蒸汽腔的发育过程,具有一定的可靠性。
2) 蒸汽驱动过程中,油藏热效率受蒸汽超覆影响较大,蒸汽超覆越强,顶底盖层散热面积越大,油藏热效率越低。
3) 蒸汽驱早期阶段,蒸汽腔在垂向上均匀扩展,蒸汽超覆程度较弱,超覆对储层热效率的影响不大;蒸汽驱中后期阶段,蒸汽超覆程度急剧增加,油藏底部蒸汽波及较少,蒸汽沿油层顶部驱替作用明显,蒸汽超覆对油藏热效率影响严重。
| [1] |
苏玉亮, 高海涛.
稠油蒸汽驱热效率影响因素研究[J]. 断块油气田, 2009, 16(2): 73–74, 82.
SU Yuliang, GAO Haitao. Influencing factors of thermal efficiency during heavy oil steam drive[J]. Fault-block Oil & Gas Field, 2009, 16(2): 73–74, 82. (in Chinese) |
| [2] |
朱维耀, 杨正明, 鞠岩, 等.
稠油藏水平井、垂直井产能分析[J]. 重庆大学学报:自然科学版, 2000, 23(sup1): 122–124.
ZHU Weiyao, YANG Zhengming, JU Yan, et al. Production evaluation for recovery heavy oil in horizontal well or vertical well[J]. Journal of Chongqing University:Natural Science Edition, 2000, 23(sup1): 122–124. (in Chinese) |
| [3] |
师耀利, 杜殿发, 刘庆梅, 等.
考虑蒸汽相变的注过热蒸汽井筒压降和热损失计算模型[J]. 新疆石油地质, 2012, 33(6): 723–726.
SHI Yaoli, DU Dianfa, LIU Qingmei, et al. A calculation model for wellbore heat loss and pressure drop considering steam phase state changing in superheated steam injection well[J]. Xinjiang Petroleum Geology, 2012, 33(6): 723–726. (in Chinese) |
| [4] | Rhee S W, Doscher T M. A method for predicting oil recovery by steamflooding including the effects of distillation and gravity override[J]. SPE Journal, 1980, 20(4): 249–266. DOI:10.2118/7547-PA |
| [5] | Jamshidnezhad M, Shen C, Kool P H, et al. Improving injectivity to fight gravity segregation in gas enhanced oil recovery[J]. SPE Journal, 2010, 15(1): 91–104. DOI:10.2118/112375-PA |
| [6] | Jamshidnezhad M.Gravity segregation in gas improved oil recovery of tilted reservoirs[C]//EUROPEC/EAGE Conference and Exhibition, 8-11 June, 2009, Amsterdam, The Netherlands.Amsterdam:Society of Petroleum Engineers, 2009:1-6. |
| [7] | Zhang X, Zhang X L.Optimisation study of production-injection ratio for steam flooding[C]//International Petroleum Technology Conference, 26-28 March, 2013, Beijing, China.Beijing:International Petroleum Technology Conference, 2013:1-8. |
| [8] |
刘振宇, 何金宝, 杨建平.
多层油藏模型在稠油热采两区数学模型上的应用[J]. 新疆石油地质, 2010, 31(3): 297–299.
LIU Zhenyu, HE Jinbao, YANG Jianping. Application of multilayer reservoir model to mathematical model for Two-Region thermal recovery[J]. Xinjiang Petroleum Geology, 2010, 31(3): 297–299. (in Chinese) |
| [9] | Marx J W, Langenheim R H. Reservoir heating by hot fluid injection[J]. TransAIME, 1959, 216(10): 312–315. |
| [10] | 刘文章. 稠油注蒸汽热采工程[M]. 北京: 石油工业出版社, 1997: 106-116. |
| [11] |
赖令彬, 潘婷婷, 秦耘, 等.
考虑蒸汽超覆的蒸汽驱地层热损失率计算方法[J]. 西北大学学报:自然科学版, 2014, 44(1): 104–110.
LAI Lingbin, PAN Tingting, QIN Yun, et al. A calculation method for heat loss considering steam overlap in steam flooding[J]. Journal of Northwest University:Natural Science Edition, 2014, 44(1): 104–110. (in Chinese) |
| [12] |
姚同玉, 李继山, 黄延章.
油藏近井地带油水两相径向渗流特征[J]. 重庆大学学报, 2013, 36(3): 141–146.
YAO Tongyu, LI Jishan, HUANG Yanzhang. Water/oil radial flow behavior near well bore zones in oil reservoir[J]. Journal of Chongqing University:Natural Science Edition, 2013, 36(3): 141–146. DOI:10.11835/j.issn.1000-582X.2013.03.024 (in Chinese) |
| [13] | 孙苗苗. 油藏多孔介质中蒸汽流动与传热本构关系研究[D]. 大庆: 大庆石油学院, 2009. |
| [14] |
鹿腾, 侯健, 孙建芳, 等.
化学辅助蒸汽驱受效剩余油分布特征研究[J]. 断块油气田, 2011, 18(6): 754–757.
LU Teng, HOU Jian, SUN Jianfang, et al. Distribution characteristics of response remaining oil in chemical-assisted steam flooding[J]. Fault-Block Oil and Gas Field, 2011, 18(6): 754–757. (in Chinese) |
| [15] |
范世通.
齐40块蒸汽驱热能综合利用分析与评价[J]. 断块油气田, 2013, 20(2): 242–245.
FAN Shitong. Comprehensive analysis and evaluation on heat efficiency of steam flooding in Block Qi 40[J]. Fault-Block Oil and Gas Field, 2013, 20(2): 242–245. (in Chinese) |
| [16] |
韩彬.
辽河油田齐40块蒸汽驱汽窜特征与控窜对策[J]. 大庆石油地质与开发, 2011, 30(6): 148–152.
HAN Bin. Characteristics and countermeasures of the steamflooding channeling in qi no.40 block of liaohe oilfield[J]. Petroleum Geology & Oilfield Development in Daqing, 2011, 30(6): 148–152. (in Chinese) |
| [17] | Lookeren J V. Calculation methods for linear and radial steam flow in oil reservoirs[J]. Society of Petroleum Engineers Journal, 1983, 23(3): 427–439. DOI:10.2118/6788-PA |
| [18] |
程浩, 郎兆新.
泡沫驱中的毛管窜流及其数值模拟[J]. 重庆大学学报:自然科学版, 2000, 23(sup1): 161–165.
CHENG Hao, LANG Zhaoxin. Capillary crossflow in foam flood and its numerical simulation[J]. Journal of Chongqing University:Natural Science Edition, 2000, 23(sup1): 161–165. (in Chinese) |
| [19] |
赖令彬, 潘婷婷.
蒸汽驱注采井间蒸汽超覆评价方法研究[J]. 特种油气藏, 2013, 20(2): 79–83.
LAI Lingbin, PAN Tingting. Evaluation method of steam override between injector and producer in steam flooding[J]. Special Oil and Gas Reservoirs, 2013, 20(2): 79–83. (in Chinese) |
| [20] | 布尔热J. 热力法提高石油采收率[M]. 杨承志, 译. 北京: 石油工业出版社, 1997: 73-106. |
 2014, Vol. 37
2014, Vol. 37


