瞬变电磁法能够穿透高阻屏蔽层，对高阻屏蔽层下覆岩层的导水构造或含水体有比较好的分辨能力，成果比较直观，近年来在矿井中应用较多。目前，全空间瞬变电磁场的理论问题主要参照文献[1]。国内矿井瞬变电磁方面主要著作是中国矿业大学于景邨的《矿井瞬变电磁法勘探》^[2]，主要研究了矿井瞬变电磁的原理以及应用在矿井中的电阻率计算等问题；中国科学院地球物理研究所的白登海、中国矿业大学岳建华、河南焦煤集团郭纯等对矿井瞬变电磁探测煤矿突水构造及数值模拟进行了研究^[3-5]；中煤科工集团西安研究院陈明生以及江苏大学闫述等研究了小线圈应用于井下探测的可行性以及探测深度等问题，并提出了小线圈也能探测大深度的论述^[6]。瞬变电磁在矿井中的应用研究文献较多，而对于瞬变电磁法在矿井井下应用中全空间与半空间瞬变电磁理论公式存在的不同之处与它们之间的关系未见明确的推导公式，大多以模拟研究为主。由于半空间瞬变电磁场在理论上比较成熟，在实践上有较多的资料可以参考，研究矿井瞬变电磁全空间和半空间之间的关系，可以利用比较来大体得出一个相应的结论，在理论上和实际探测工程应用上具有重要的参考价值。笔者主要在整理前人研究成果的基础上，延伸推导全空间瞬变电磁公式，并与半空间瞬变电磁场进行比较，发现了矿井瞬变电磁场的倍数现象，并对倍数现象进行了阐述和应用。

1 均匀全空间磁偶极子形成的瞬变电磁场

阶跃电流断开时时间域电磁场磁场分量的表达式^[7]，

$ {H_R} = \frac{M}{{2{\rm{ \mathsf{ π} }}{R^3}}}\left[ {\varphi \left( u \right) - \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} u{{\rm{e}}^{ - \left( {{u^2}/2} \right)}}} \right]\cos \theta , $

(1)

式中：H_R为全空间瞬变磁场分量；M为发送回线的磁距；R为偶极源到观测点的距离；u为感应数，$u = 2{\rm{ \mathit{ π} }}R/\sqrt {2{\rm{ \mathit{ π} }}\rho t \times {{10}^7}} $；θ为R方向与z方向之间的夹角；$\varphi (u) = \sqrt {\frac{2}{{\rm{ \mathit{ π} }}}} \int_0^u {{{\rm{e}}^{-({t^2}/2)}}{\rm{d}}t} $为概率积分。

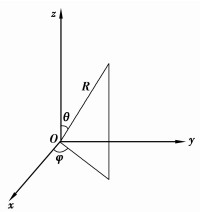
在数学上，球坐标与直角坐标坐标变换有如式(2)所示公式。球坐标和直角坐标变换如图 1所示。

坐标变换

$ \left\{ \begin{array}{l} x = R\sin \theta \cos \varphi \\ y = R\sin \theta \sin \varphi \\ z = R\cos \theta \end{array} \right.。$

(2)

对于全空间瞬变电磁磁场强度由式(1)变换到直角坐标下即为

$ {H_z} = \frac{M}{{2{\rm{ \mathsf{ π} }}{R^3}}}\left[ {\varphi \left( u \right) - \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} u{{\rm{e}}^{ - \left( {{u^2}/2} \right)}}} \right]。$

(3)

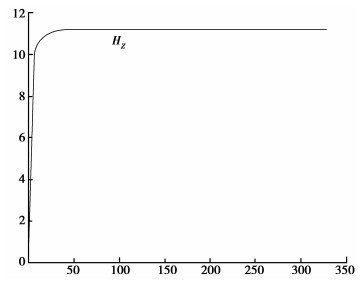
以式(3)为基础，以u是横坐标，给予各个变量以定值，M=500 A·m²，电阻率ρ=1 000 Ω·m，R=2 m，编程可以求出全空间瞬变场磁场强度随u变化的基本形态如图 2所示。

从图 2可以看出，全空间瞬变场磁场强度随着u的增大而迅速增加，直到达到一定的数值之后不再变化。从电场断电的角度来讲，由于存在关系式$u = 2{\rm{ \mathit{ π} }}R/\tau = 2{\rm{ \mathit{ π} }}R/\sqrt {2{\rm{ \mathit{ π} }}\rho t \times {{10}^7}} $，也就是说全空间瞬变场在早期u→∞，t→0时，这时电流刚断开，其场强达到一个最大值；随后随着时间的增加，接近到u→0，t→∞时，其瞬变场也随之迅速减小，直到仪器观测不到信号为止，这种变化特性符合实际规律。

在早期条件下，研究偶极源电流刚断开时瞬变耦合的早期特性。u→∞，φ(u)→1，式(3)就变为

$ H_{z\;早}^{\rm{f}} = \frac{M}{{2{\rm{ \mathsf{ π} }}{R^3}}}。$

(4)

式(4)即为早期全空间条件下垂直磁偶源产生的瞬变电磁磁场强度。

下面研究在晚期条件下的瞬变电磁场。为了研究瞬变耦合的晚期特性，应当把概率积分展成u的级数，u是一个较小参数，

$ \varphi \left( u \right) \approx \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( {u - \frac{{{u^3}}}{{3!}} + \frac{{3{u^5}}}{{5!}}} \right), $

(5)

$ {{\rm{e}}^{ - \left( {{u^2}/2} \right)}} \approx \left( {1 - \frac{{{u^2}}}{2} + \frac{{{u^4}}}{8}} \right)。$

(6)

把此级数近似表达式式(5)和式(6)，代入式(3)，就能得到晚期磁场表达式

$ H_z^{\rm{f}} = \frac{M}{{12{\rm{ \mathsf{ π} }}\sqrt {\rm{ \mathsf{ π} }} }}\frac{{{\mu ^{3/2}}{\sigma ^{3/2}}}}{{{t^{3/2}}}}。$

(7)

由文献[1]可知，在u < 0.2时，这些表达式能以合理的精度来描述这种场。这时，R/τ < 0.318×10^-1，亦即τ/R>1/0.318×10^-1≈31。式(7)即为磁偶极源晚期全空间瞬变电磁晚期响应公式。

2 均匀半空间磁偶极子形成的瞬变电磁场

当场源为阶跃函数电流激发的垂直轴磁偶极子时，在均匀半空间表面上观测的似稳瞬变电磁场磁场分量的表达式为^[7-16]

$ B_z^{\rm{h}} = \frac{{\mu M}}{{4{\rm{ \mathsf{ π} }}{r^3}}}{b_z}, $

(8)

式中：r为偶极装置的偶极距；M为发送回线的磁距；μ=4π×10^-7 h/m，为空气磁导率；ρ为均匀大地的电阻率。b_z为u的函数，具体表达式如下：

$ {b_z} = 1 - \left( {1 - \frac{9}{{{u^2}}}} \right)\varphi \left( u \right) - \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} {{\rm{e}}^{ - \left( {{u^2}/2} \right)}}\left( {\frac{9}{u} + 2u} \right)。$

(9)

式(8)描述的是场源电流接通时刻t=0的场分量。为了获得电流断开时各个场分量的表达式，必须从1中减掉函数b_z。令b_z^′=1-b_z，则有：

$ {{b'}_z} = \left( {1 - \frac{9}{{{u^2}}}} \right)\varphi \left( u \right) + \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} {{\rm{e}}^{ - \left( {{u^2}/2} \right)}}\left( {\frac{9}{u} + 2u} \right)。$

(10)

由式(8)及式(10)可知，半空间瞬变电磁场在电流断开时的磁场强度H_z^h′为

$ H_z^{{\rm{h'}}} = \frac{{\mu M}}{{4{\rm{ \mathsf{ π} }}{r^3}}}\left\{ {\left[ {\left( {1 - \frac{9}{{{u^2}}}} \right)\varphi \left( u \right)} \right] + \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( {\frac{9}{u} + 2u} \right){{\rm{e}}^{ - \left( {{u^2}/2} \right)}}} \right\}。$

(11)

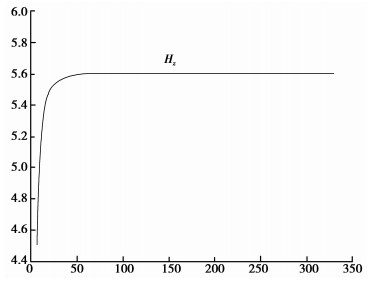
以式(11)为基础，以u是横坐标，给予各个变量以定值，定值的取值同全空间取值相同，M=500 A·m²，电阻率ρ=1 000 Ω·m，r=2 m，仅保留u作为变量，通过编程可以求出半空间瞬变场磁场强度的基本形态如图 3所示。

从图 3可以看出，半空间瞬变场磁场强度同全空间瞬变场存在着相似的衰减关系，也是随着u的增大而迅速增加，直到达到一定的数值之后不再变化。对比图 2和图 3得知，全空间瞬变磁场最大值约为半空间瞬变磁场的两倍，曲线形态基本类似，也是在电流断开瞬间达到最大值，随后迅速减小。

在早期条件下，考虑瞬变场耦合早期参数τ/r较小时各个场分量的特征，得到

$ H_{z\;早}^{{\rm{h'}}} = \frac{M}{{4{\rm{ \mathsf{ π} }}{r^3}}}\left( {1 - \frac{9}{{{u^2}}}} \right)。$

(12)

在晚期条件下u→0，利用式(5)、式(6)和式(11)可以得到

$ H_z^{\rm{h}} \approx \frac{M}{{30{\rm{ \mathsf{ π} }}\sqrt {\rm{ \mathsf{ π} }} }}{\left( {\frac{{\sigma \mu }}{t}} \right)^{3/2}}。$

(13)

由文献[1]可得出，在τ/r>16时，式(13)可以以合理的精度来描述这种电磁场。

3 矿井瞬变电磁场的倍数现象

发射线圈与接收线圈处于同一平面时θ=90°，满足Rsinθ=r，即R=r。定义磁偶源全空间瞬变电磁场与半空间瞬变电磁的磁场强度比值为K_w，利用式(3)和式(11)，则K_w有：

$ {K_{\rm{w}}} = \frac{{H_z^{\rm{f}}}}{{H_z^{{\rm{h'}}}}} = \frac{{\varphi \left( u \right) - \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} u{{\rm{e}}^{ - \left( {{u^2}/2} \right)}}}}{{\frac{1}{2}\left[ {\left( {1 - \frac{9}{{{u^2}}}} \right)\varphi \left( u \right) + \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( {\frac{9}{u} + 2u} \right){{\rm{e}}^{ - \left( {{u^2}/2} \right)}}} \right]}}。$

(14)

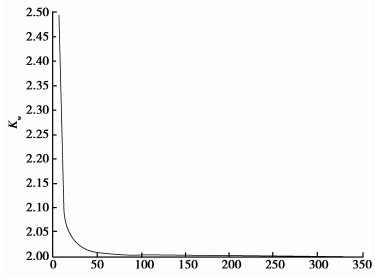
基于式(14)进行编程，得到了全空间和半空间磁场强度比值K_w的曲线。以u是横坐标，磁场强度比值K_w基本形态如图 4所示。

从图 4可以看出，全空间和半空间磁场强度比值K_w在2~2.5之间变化。u和t存在着关系式$u = 2{\rm{ \mathit{ π} }}r/\sqrt {2{\rm{ \mathit{ π} }}\rho t \times {{10}^7}} $，因此在u→0时，t→∞，则K_w趋于2.5，这时就是瞬变电磁全空间和半空间晚期磁场的比值；在u→∞时，t→0，则K_w趋于2，这时就是瞬变电磁全空间和半空间早期磁场的比值。中间过渡区域则为中期的瞬变电磁比值。该图很好的揭示了全空间瞬变电磁和半空间瞬变电磁磁场强度比值变化关系，为研究晚期全空间磁场理论提供了有力的证明。

3.1 瞬变电磁场早期倍数现象

在早期中，研究偶极源电流刚断开时瞬变耦合的早期特性。u→∞，φ(u)→1，e^(-u2/2)→0，则有

$ K_{\rm{w}}^{早} = \frac{{\left[ {\varphi \left( u \right) - \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} u{{\rm{e}}^{ - \left( {{u^2}/2} \right)}}} \right]}}{{\frac{1}{2}\left\{ {\left[ {\left( {1 - \frac{9}{{{u^2}}}} \right)\varphi \left( u \right)} \right] + \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( {\frac{9}{u} + 2u} \right){{\rm{e}}^{ - \left( {{u^2}/2} \right)}}} \right\}}} \approx 2。$

(15)

即早期条件下，磁偶源瞬变电磁全空间磁场强度是半空间磁场强度的2倍。这是因为全空间条件下，当电流刚断开时，传导电流最初集中在场源附近，并力图维持有电流流动时同样的磁场。但是在电流刚刚断开时的半空间磁场响应也主要集中在场源附近，这是由于此时的半空间一次场强度为全空间的一半，因此对应的其二次场磁场强度也为全空间的一半。

3.2 瞬变电磁场晚期倍数现象

在晚期中，可以利用式(5)和式(6)。全空间瞬变电磁场公式(3)中，定义函数${b^{\rm{f}}} = \varphi (u)-\sqrt {\frac{2}{{\rm{ \mathit{ π} }}}} u{e^{-({u^2}/2)}}$，则有${b^{\rm{f}}} = \sqrt {\frac{2}{{\rm{ \mathit{ π} }}}} \left[{u-\frac{{{u^3}}}{6}-u(1-\frac{{{u^2}}}{2})} \right] = \frac{{{u^3}}}{3}\sqrt {\frac{2}{{\rm{ \mathit{ π} }}}} $。

半空间，电流断开时，利用式(13)，则有$b{'_z} \approx \frac{1}{2}\left\{ {\left[{\left( {1-\frac{9}{{{u^2}}}} \right)\sqrt {\frac{2}{{\rm{ \mathit{ π} }}}} \left( {u-\frac{{{u^3}}}{6} + \frac{{{u^5}}}{{40}}} \right)} \right] + \sqrt {\frac{2}{{\rm{ \mathit{ π} }}}} \left( {\frac{9}{u} + 2u} \right)} \right.$。$\left. {\left( {1-\frac{{{u^2}}}{2} + \frac{{{u^4}}}{8}} \right)} \right\} \approx \frac{2}{{15}}\sqrt {\frac{2}{{\rm{ \mathit{ π} }}}} {u^3}$。

晚期磁偶源瞬变电磁磁场强度全空间和半空间比较，

$ K_{\rm{w}}^{晚} = \frac{{\frac{1}{3}\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} {u^3}}}{{\frac{2}{{15}}\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} {u^3}}} = \frac{{15}}{6} = 2.5。$

(16)

即晚期条件下，磁偶源瞬变电磁全空间磁场强度是半空间磁场强度的2.5倍。这是因为全空间条件下，当电流断开一段时间以后，涡流场逐渐减弱，在全空间状态下，接收来自全空间的磁场。而在半空间中，主要接收来自地下的磁场，电流断开初期，半空间与全空间存在着一半的关系，随着磁场逐渐衰弱，这种一半的关系被打破，而到了晚期，半空间和全空间磁场衰减均趋于稳定的比值，但是不再是一半的关系，而是0.4倍的关系，该比值也可以从图 3中得到证明。

需要指出的是，晚期公式比较是有条件的，即满足全空间瞬变磁场计算精度情况下，有τ/r>31；满足半空间瞬变磁场计算精度情况下，有τ/r>16，因此，满足公式比较的条件是这两个集合的交集：

$ \left\{ {\left( {\tau /r > 31} \right) \cap \left( {\tau /r > 16} \right)} \right\} = \left\{ {\tau /r > 31} \right\}。$

由于$\tau /r = \sqrt {2{\rm{ \mathit{ π} }}\rho t \times {{10}^7}} /r > 31$，假如矿井瞬变电磁仪器r=1.5 m，ρ=1 000 Ω·m，则有t>2.3×10^-8 s。在目前的矿井瞬变电磁仪器中，一般应用t>100 μs，因此，这个时间t对于矿井瞬变电磁勘探晚期数据来说，已经足够精确，晚期推导的公式及其相关关系也可以适应。

这个倍数关系也可以从瞬变电磁磁偶极源晚期得到的公式进行比较得到。

由式(7)和式(13)可以得出磁偶极源晚期全空间与半空间磁场强度比值K_H为

$ {K_{\rm{H}}} = \frac{{H_z^{\rm{f}}}}{{H_z^{\rm{h}}}} \approx \frac{{\frac{M}{{12{{\rm{ \mathsf{ π} }}^{3/2}}}}\frac{{{\mu ^{3/2}}{\sigma ^{3/2}}}}{{{t^{3/2}}}}}}{{\frac{M}{{30{\rm{ \mathsf{ π} }}\sqrt {\rm{ \mathsf{ π} }} }}{{\left( {\frac{{\sigma \mu }}{t}} \right)}^{3/2}}}} = 2.5。$

(17)

同样得到，磁偶极源晚期全空间的磁场强度约为半空间磁场强度的2.5倍。

假设感应电压一样，则利用式(7)和式(13)，可以得出磁偶极源晚期全空间和半空间视电阻率的比较，

$ {K_\rho } = {\rho _{\rm{f}}}/{\rho _{\rm{h}}} \approx {\left( {2.5} \right)^{2/3}} \approx 1.842。$

(18)

即磁偶极源晚期全空间视电阻率约为半空间视电阻率的1.842倍。这个倍数关系在文献[7]中也被证明是正确的。

同样也可以推导全空间瞬变电磁探测深度估算公式为

$ {d^{\rm{f}}} \approx 0.66{\left( {\frac{{IA}}{{\sigma {\eta _{\rm{v}}}}}} \right)^{1/5}}。$

(19)

根据上面分析，可以得出磁偶极源晚期全空间和半空间瞬变电磁场存在倍数关系，即磁偶极源晚期全空间的磁场强度约为半空间磁场强度的2.5倍，全空间的电场强度约为半空间电场强度的2.5倍，全空间视电阻率约为半空间视电阻率的1.842倍，全空间瞬变电磁场探测深度为半空间的1.2倍。

3.3 矿井瞬变电磁场倍数现象

矿井瞬变电磁场介于全空间和半空间之间，因此可以推出矿井瞬变电磁磁偶极源晚期磁场强度和电场强度为半空间磁场强度和电场强度的n倍(1 < n < 2.5)，总结矿井瞬变电磁磁偶极源晚期的倍数现象即为：磁偶极源晚期矿井瞬变电磁的磁场强度H_m、电场强度E_m、探测深度d_m、计算视电阻率ρ_m分别为半空间瞬变电磁场晚期的磁场强度H^h、电场强度E^h、探测深度d_h、计算视电阻率ρ_h倍数。

矿井瞬变电磁倍数现象的公式表达为

$ \left\{ \begin{array}{l} {H_{\rm{m}}} = {n_1}{H^{\rm{h}}}\\ {E_{\rm{m}}} = {n_2}{E^{\rm{h}}}\\ {d_{\rm{m}}} = {n_3}{d_{\rm{h}}}\\ {\rho _{\rm{m}}} = {n_4}{\rho _{\rm{h}}} \end{array} \right.。$

(20)

式中，n₁、n₂、n₃、n₄分别为矿井瞬变电磁的磁场强度常数、电场强度常数、探测深度常数、计算视电阻率常数，其取值范围为1 < n₁ < 2.5，1 < n₂ < 2.5，1 < n₃ < 1.2，1 < n₄ < 1.842，取值的具体大小可以根据井下实测煤体或岩体的属性来确定，晚期条件τ/r>31。

根据倍数现象，可以得出其他一些重要的结论。由于矿井瞬变电磁磁场强度比半空间大，则其感应电动势也变大，提高了信噪比，对应的探测深度也增大了，比采用半空间瞬变电磁计算要有优势。另外全空间瞬变电磁二次场晚期的磁场强度和电场强度均为半空间的2.5倍，而不是2倍，这在理论上说明全空间瞬变电磁二次场的磁场强度和电场强度不能简单用半空间的公式套用2倍来计算，不是简单的叠加关系，这是计算全空间瞬变电磁场尤其注意的地方。

4 工程应用

目前，全国有很大一部分煤矿受小煤窑老空区的水体威胁。由于小煤窑没有准确的勘查资料，而且井下巷道走向弯曲。随着时间的推移，老空区积水越来越严重，尤其是在山西整合煤矿方面表现最为突出。

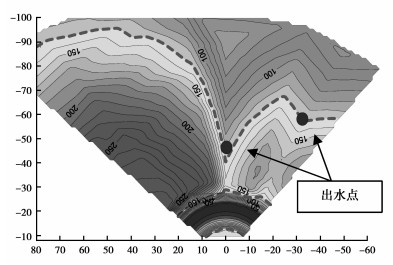
采用矿井瞬变电磁仪进行探测，可以查清井下积水区域^[17-22]。在采用倍数现象进行解释分析数据时，主要体现在探测深度和计算视电阻率上。考虑到井下巷道的影响较小，井下瞬变电磁倍数关系可以简化取右边界数值。一般井下探测工程在探测深度上采用公式(19)计算，约为半空间的1.2倍；计算视电阻率一般取半空间的1.842倍，准确的矿井瞬变电磁晚期视电阻率计算系数取值原则一般是先测定待测煤层的电阻率ρ_coal(可以用电法、雷达等方法测定，一般煤矿煤层电阻率值在开采前已经测定)，然后利用半空间瞬变电磁公式做试验，得出ρ_h，根据ρ_coal、ρ_h得出井下瞬变电磁视电阻率计算系数K_m，如果按照半空间瞬变电磁法计算出来的视电阻率偏小，但是对探测异常影响不大；井下其他参数可以参考半空间的处理方式，无需过多处理。图 5为山西长平煤矿探测成果图，探测地点为该矿回风巷掘进工作面。测线布置从掘进头朝左50°起至朝右50°，以10°为差值布置测线，共探测11个点。

采空区在充水的情况下，视电阻率等值线较大范围呈现低阻，视电阻率具体值与含水情况有关，且低阻异常连续性较好；若含水较大，电磁波一般不宜穿过，表现为等值线图上为深部全部为低阻异常。探测位置打钻孔2个，打正前方50 m出水，右侧30°前方65 m出水；验证准确。说明应用倍数现象对矿井瞬变电磁探测可以更为准确的探测异常。

5 结论

1) 早期全空间瞬变电磁磁场强度是半空间瞬变电磁场磁场强度的2倍；晚期在τ/r>31区间内，全空间瞬变电磁场磁场强度是半空间瞬变电磁场磁场强度的2.5倍；中间过渡区域比值介于2~2.5之间。

2) 发现了矿井瞬变电磁场的倍数现象，即为磁偶极源晚期矿井瞬变电磁场的磁场强度H_m、电场强度E_m、探测深度d_m、计算视电阻率ρ_m分别为半空间瞬变电磁场场晚期的磁场强度H^h、电场强度E^h、探测深度d_h、计算视电阻率ρ_h倍数，公式表达为H_m=n₁H^h，E_m=n₂E^h，d_m=n₃d_h，ρ_m=n₄ρ_h，其中1 < n₁ < 2.5，1 < n₂ < 2.5，1 < n₃ < 1.2，1 < n₄ < 1.842。

3) 通过实例验证，应用倍数现象对矿井瞬变电磁探测可以更为准确的探测异常。

比较磁偶极源晚期全空间和半空间瞬变电磁场磁场强度的特征得出的矿井瞬变电磁场倍数现象具有重要的指导性意义。由于半空间瞬变电磁场场在理论上比较成熟，在实践上有较多的资料可以参考，对于矿井瞬变电磁场在晚期的特征就可以利用比较来大体得出一个相应的结论。在实际探测工程应用上也具有很重要的参考价值。

6 致谢

本文得到了中南大学温佩琳教授和中煤科工集团西安研究院陈明生教授的指导，在此表示感谢。