2. 深圳供电局有限公司, 广东 深圳 518000
2. Shenzhen Power Supply Co. Ltd., Shenzhen, Guangdong 518000, China
中压配电网的中性点接地方式与系统的供电可靠性、电力系统过电压与绝缘配合、继电保护、通讯信号系统的干扰、电气安全以及接地装置等密切相关[1-2]。在发生故障时,中性点不接地系统的单相接地电流仅由系统对地电容决定,多数情况下可以自动消除,但间歇性电弧接地过电压较大,要求较高的绝缘水平。经消弧线圈接地系统,单相接地故障电流仅为补偿后很少的残余电流,对电弧的重燃有明显的抑制作用,可减少高幅电弧接地发生过电压的几率,但调节脱谐度麻烦且尚未实现100%准确故障选线,会严重影响正常供电的恢复[3-4]。经小电阻接地能够有效抑制谐振过电压及弧光接地过电压,工频过电压较低,线路和设备的绝缘水平要求比经消弧线圈接地的绝缘水平低,单相接地故障的检出灵敏度高,费用较消弧线圈小,但也因接地故障电流大,使电位上升较高,对人身设备安全不利,且保护迅速动作切除故障,会间断供电[5]。
合理选择一种既保证电网安全可靠又不至于造成较大的经济投资的中性点接地方式对电网安全高效运行具有重大意义。大量文献针对中性点接地方式的影响进行了研究。文献[6-8]根据苏州、武汉及贵州地区配电网的电容电流大小,提出了适宜采用的中性点接地方式。文献[9-10]重点分析中性点经小电阻接地及经消弧线圈接地2种方式的优缺点,指出小电阻接地方式在供电可靠性上依赖于网架结构及自动化程度,而消弧线圈接地方式通过优化自动调谐装置,将具有较优越的技术经济性。文献[11]指出电网结构及变压器组别对接地方式选择的影响,比较中性点经消弧线圈及中性点经小电阻接地方式的优缺点,给出中性点接地方式选择的一般意见。
目前中压配电网的中性点接地方式的选择主要通过不同中性点接地方式影响的简单对比来实现,尚缺乏定量的中性点接地方式决策方法。文献[12]采用专家评分方式得出影响中性点接地方式选择因素的权系数,加权不同中性点接地方式各因素的相对值,选择加权合计值最大的接地方式。文献[13]根据中性点接地方式的影响因素,建立相应隶属度函数,通过模糊原理建立中性点接地方式决策方法。文献[14]通过对比不同中性点接地方式的故障跳闸率相对优势度大小评价中性点接地方式。文献[15]采用加权多指标区间灰耙算法评价各中性点接地方式下配电网可靠性水平的优劣,以靶心距最小的方案为最优。
中性点接地方式决策方法的缺乏对电网规划及运行造成较大影响。文中提出综合中性点接地方式对配电网可靠性、安全性及经济性的影响,将不同中性点接地方式下配电网的可靠性评价及计入安全性因素的经济运行成本相结合,计算不同中性点接地方式下配电网的全寿命周期成本并结合可靠性指标为约束条件来实现中性点接地方式决策。
1 中性点接地方式决策方法本决策方法利用最优化思想,以经济性指标最优为目标函数、可靠性指标为约束条件建立中性点接地方式决策模型。其目标函数为
| $ \min \;W = G + X + K + F, $ | (1) |
约束条件为
| $ \left. {\begin{array}{*{20}{l}} {{A_{{\rm{ASAI}}}} \ge {A_\mathit{\Gamma }}}\\ {{C_{{\rm{CAIDI}}}} \le {C_\mathit{\Gamma }}}\\ \begin{array}{l} \left| {{P_j}} \right| \le {P_{j\max }}\\ {U_{j\min }} \le {U_j} \le {U_{j\max }} \end{array}\\ {{I_{ij}} \le {I_{ij\max }}}\\ {{P_j} = {q_j} + \sum\limits_{k = 1}^{{L_j}} {{P_{jk}}} } \end{array}} \right\}, $ | (2) |
式中:W为各中性点接地方式下的全寿命周期成本;G为计及安全性因素的设备投入费用;X维护检修费用;K为停电损失费用;F为废弃成本,这些费用均为等年值[16];AASAI为各中性点接地方式下的系统平均供电可用率;CCAIDI为各中性点接地方式下的用户平均停电持续时间;AΓ为实际网络对应要求的平均供电可用率指标值;CΓ为实际网络对应要求的用户平均停电持续时间指标值;Pj和Pjmax分别为向第j个负荷节点输送的功率和最大允许功率;Ujmin和Ujmax分别为第j个负荷节点电压最大、最小限值;qj为第j个负荷节点的负荷量,Lj为负荷节点总数,Pjk为由第j个负荷节点供电的第k条线路的功率;Iij和Iijmax为线路lij的电流及最大允许电流。
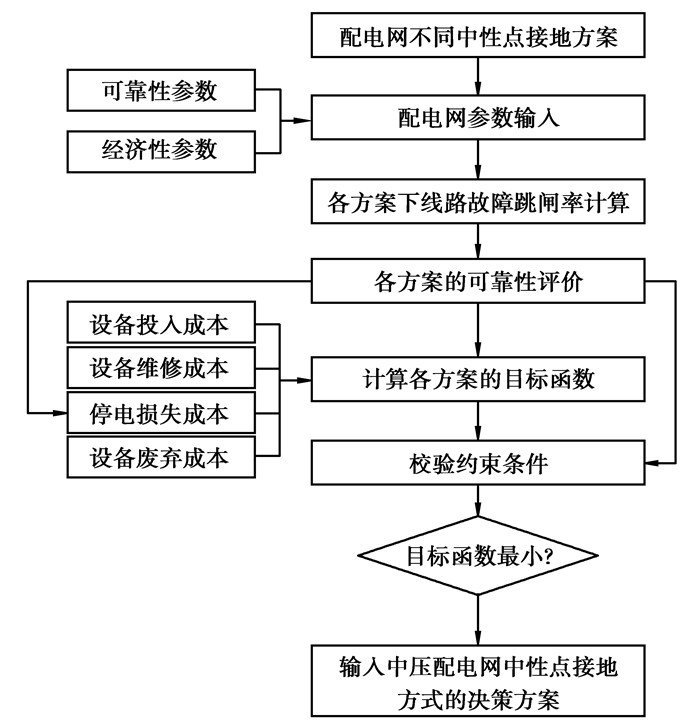
该决策方法计及不同中性点接地方式对配电网可靠性的影响,利用可靠性参数进行不同中性点接地方式下配电网可靠性评价。将可靠性评价指标中的缺失电量指标转化为停电损失费用,做为目标函数中计及可靠性因素的成本,将系统供电可用率及用户平均停电持续时间指标作为可靠性约束条件。决策流程如图 1所示。
|
图 1 中性点接地方式决策流程图 |
研究采用禁忌搜索[17]算法求解最优方案,步骤如下:
1) 生成初始中性点接地方案,形成领域结构;
2) 输入参数,置禁忌表TL=φ;
3) 计算目标函数,选取目标函数最优的方案作为当前最优方案Xbest=X0,并将初始中性点接地方案列入禁忌表中;
4) 产生nnei种相邻方案,相邻方案是根据领域结构中不同变量内的变动而产生,相邻方案与初始方案只在一个变量上发生了变化,且禁忌表中的方案不能作为相邻方案;
5) 计算各个相邻方案的约束条件指标,其是否满足约束条件。对于不满足约束条件的相邻方案,在其目标函数中附加上极大的惩罚值;
6) 计算相邻方案的目标函数,若此时最优目标函数小于当前最优方案的目标函数,则替换该相邻方案为当前最优方案Xbest=X*;
7) 若终止条件不满足,则继续步骤4),否则输出当前最优方案作为中性点接地方案。
2 中性点接地方式决策的目标函数 2.1 计及安全性因素的设备投入费用G计及安全性因素的设备投入成本包括初期固定的设备投资和运行中添加的设施投资为
| $ G = \sum\limits_{i = 1}^m {\left[{\frac{{k\left( {1 + k} \right){n_i}}}{{{{\left( {1 + k} \right)}^n}-1}}{p_i} + {a_i}} \right]}, $ | (3) |
式中:m为投资的总项数;ni为第i项投资的使用年限;k为年利率;pi为第i项投资的初期投资;ai为每项投资所需的运行成本。
针对不同中性点接地方案,计及安全性因素的初期投资主要包括中性点接地装置、继电保护装置、绝缘装置、自动化装置及选线装置等的购置费、与之配套的工程费用及其他费用等。其中,继电保护装置、绝缘装置及自动化装置投资等都与安全性因素息息相关,如采用价格昂贵的绝缘电缆线可减少人身触电危险。
计及安全性因素的运行投资主要是指增设安全防护设施的投资。包括保证人身安全装设的安全防护栏、电缆沟道与人行道距离等的规划建设投资等。
2.2 维护检修费用X维护检修费用包括故障所产生的维修费用,及定期巡检维护费用为
| $ X = \sum\limits_{i = 1}^n {{J_i}}, $ | (4) |
式中:n为每年维护检修任务的总项数;Ji为第i项维护检修任务的费用,包括相应的材料费及人工费。
2.3 停电损失费用K根据缺供电量,考虑分析地区的产电比及年停电总损失的可靠性惩罚系数[18],可计算停电损失成本为
| $ K = a \times {E_{{\rm{ENS}}}} \times c, $ | (5) |
式中:EENS为各中性点接地方式下的缺供电量,可由不同中性点接地方式下的可靠性评估获得;α为年停电总损失的可靠性惩罚系数,通常取值为1~2;c为地区的产电比,是指一个地区在一年内创造的产值(用货币形式表示)与消耗的电量之比为
| $ c = {G_{{\rm{GD}}{{\rm{P}}_i}}}/{\mathit{E}_{{\rm{E}}{{\rm{C}}_i}}}, $ | (6) |
式中:GGDPi为区域当年用价格表示的国内生产总值;EECi为区域一年的总用电量。
2.4 废弃成本F废弃成本为
| $ F = \sum\limits_{i = 1}^p {\left[{\frac{{k\left( {1 + k} \right){n_i}}}{{{{\left( {1 + k} \right)}^n}-1}}{Q_i}} \right]}, $ | (7) |
式中:p为总的设备数;Qi为第i种设备的废弃成本;ni为第i种设备的使用年限;k为年利率。
3 可靠性指标计算不同中性点接地方式在配电网发生单相接地故障时,对线路元件的故障跳闸率、停运时间及故障扩展影响差异如表 1所示[19]。
| 表 1 不同中性点接地方式对配电网可靠性的影响 |
假设在配电网中,线路i的故障率为λ;线路i故障为单相接地短路故障的比率为η;线路i故障为瞬时性单相接地故障的比率为δ;线路i发生过电压事故扩展的概率为e1;线路i发生电弧火灾事故扩展的概率为e2;瞬时性电弧成功熄灭的概率为σ;中性点经消弧线圈接地时能够成功熄灭瞬时性电弧的概率为α;中性点经小电阻接地时保护无法成功发出跳闸信号的概率为β;小电阻接地方式下重合闸成功率为θ;中性点经高阻接地时保护成功发出跳闸信号的概率为ζ;微机选线正确率为ω。建立各中性点接地方式下的线路故障跳闸率模型如下。
3.1 中性点不接地故障跳闸率线路i故障的跳闸率为
| $ {P_{ii}} = \lambda \eta \left( {1-\delta } \right) + \lambda \left( {1-\eta } \right) = \lambda \left( {1-\eta \delta } \right), $ | (8) |
线路i故障时故障扩展使正常线路j故障的跳闸率为
| $ {P_{ii}} = \lambda \eta \left( {1-\delta } \right)\left( {{e_1} + {e_2}-{e_1}{e_2}} \right)。$ | (9) |
线路i故障的跳闸率为
| $ {P_{ii}} = \lambda \eta \delta \left( {1-a} \right) + \lambda \eta \left( {1-\delta } \right) + \lambda \left( {1-\eta } \right) = \lambda \left( {1 - \eta \delta a} \right), $ | (10) |
线路i故障时故障扩展使正常线路j故障的跳闸率为
| $ {P_{ii}} = \left[{\lambda \eta \delta \left( {1-a} \right) + \lambda \eta \left( {1-\delta } \right)} \right]\left( {{e_1} + {e_2} -{e_1}{e_2}} \right)。$ | (11) |
线路i故障的跳闸率为
| $ {P_{ii}} = \lambda \eta \delta \left( {1-\beta } \right)\left( {1-\theta } \right) + \lambda \eta \left( {1-\delta } \right)\left( {1 - \beta } \right) + \lambda \left( {1 - \eta } \right) = \lambda \left( {1 - \eta \beta - \eta \delta \theta + \eta \beta \delta \theta } \right), $ | (12) |
线路i故障使正常线路j故障的跳闸率为
| $ {P_{ii}} = \lambda \eta \delta \beta + \lambda \eta \left( {1-\delta } \right)\beta = \lambda \eta \beta 。$ | (13) |
线路i故障的跳闸率为
| $ {P_{ii}} = \lambda \eta \delta \left( {1-\sigma } \right)\left( {1-\xi } \right) + \lambda \eta \left( {1-\delta } \right)\left( {1 - \xi } \right) + \lambda \left( {1 - \eta } \right) = \lambda \eta \delta \sigma \left( {1 - \xi } \right) + \lambda \left( {1 - \xi \eta } \right), $ | (14) |
线路i故障使正常线路j故障的跳闸率为
| $ {P_{ii}} = \left[{\lambda \eta \delta \left( {1-\sigma } \right) + \lambda \eta \left( {1-\delta } \right)} \right]\xi \left( {{e_1} + {e_2} -{e_1}{e_2}} \right)。$ | (15) |
线路i最终的跳闸率Pi等于自身故障的跳闸率及其他邻线故障时发生扩展引起线路i故障的跳闸率。
根据不同中性点接地方式下故障跳闸率、故障停运时间及停运造成的负荷损失进行配电网可靠性评价,计算决策模型中需要的平均供电可用率AASAI、用户平均停电持续时间CCAIDI及缺供电量EENS3个指标[20]。各指标的计算式为
| $ {A_{{\rm{ASAI}}}}{\rm{ = }}\frac{{\sum\limits_i^m {8760{N_i}}-\sum\limits_i^m {{U_i}{N_i}} }}{{\sum\limits_i^m {8760{N_i}} }}, $ | (16) |
| $ {C_{{\rm{CAIDI}}}}{\rm{ = }}\frac{{\sum\limits_i^m {U{U_{{\rm{SL}}i}}{N_i}} }}{{\sum\limits_i^m {f{U_{{\rm{SL}}i}}{N_i}} }}, $ | (17) |
| $ {E_{{\rm{ENS}}}} = \sum\limits_i^m {{P_{ai}}{U_{{\rm{SL}}i}}}, $ | (18) |
式中:m为总的负荷点数;Ni为负荷点i的用户数;USLi为负荷点i的每年停运总时间;fUSLi为负荷点i的停运率;Pai为负荷点i的平均负荷。
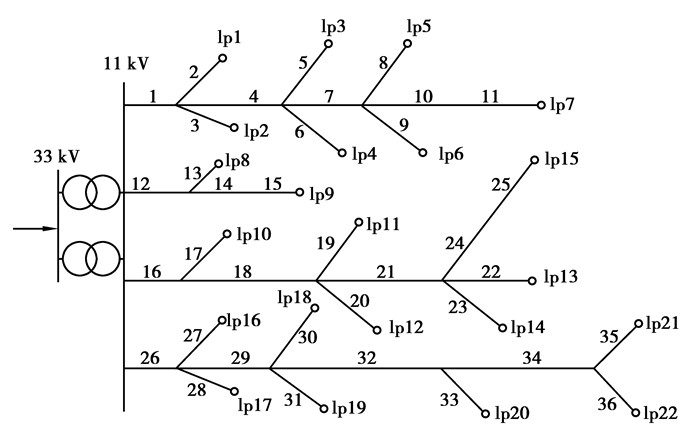
4 算例图 2为RBTS Bus2系统,是由2台主变、4条馈线、36条线路、22个负荷点和配电变压器组成的33/11 kV中压配电系统[21]。线路均为电缆[22],参数为:λ=0.04,r=8,η=0.8,δ=0.55,α=0.9,β=0.01,ζ=0.2,e1=e2=0.1,m=2,ω=0.5,θ=0.5。假设该网络的可靠性指标规范为:AΓ=99.96%,CΓ=3.5 h。设各设备的使用年限n=20年,年利率k=5%,产电比c=5.27元/kWh,可靠性惩罚系数α=1.5。
|
图 2 RBTS Bus2系统图 |
计算图 2所示网络在不同中性点接地方案下的可靠性指标,结果如表 2所示。其中,中性点经小电阻接地方式的供电可用率较高,用户停电持续时间及缺供电量较小;中性点不接地、经消弧线圈接地及经高电阻接地方式的系统供电可用率、用户停电持续时间及缺供电量指标相差不大,可靠性水平低于中性点经小电阻接地方式。
| 表 2 不同中性点接地方式下的可靠性指标 |
结合实际运行统计数据及电力建设工程概算定额[23-24],获得不同中性点接地方案的各项投入费用如表 3所示。计算不同中性点接地方式的总投入费用如表 4所示。
| 表 3 不同中性点接地方式下的设备投入费用 |
| 表 4 不同中性点接地方案的年投入成本 |
根据统计资料得到不同中性点接地方案的年维修费用,如表 5所示。
| 表 5 不同中性点接地方案的年维修费用 |
根据不同中性点接地方式下的系统缺失电量指标,得到不同中性点接地方式下的年停电损失费用如表 6所示。
| 表 6 不同中性点接地方案的年停电损失费用 |
根据实际运行经验得到不同中性点接地方案的年废弃成本,如表 7所示。
| 表 7 不同中性点接地方案的年废弃成本 |
根据决策流程,计算不同中性点接地方式如图 2所示网络的目标函数,结果如表 8所示。
| 表 8 同中性点接地方案的总经济成本 |
中性点经消弧线圈接地及经高电阻接地方式的目标函数较大,中性点经小电阻接地与不接地的目标函数相对较小。在可靠性水平均满足约束条件的情况下,中性点经小电阻接地方式的可靠性水平最高且目标函数为4种中性点接地方案中最优,因此对于图 2所示网络推荐采用中性点经小电阻接地方式。
5 结论随着电网的发展,中性点接地方式已多元化,寻找一种综合考虑电网供电可靠性、安全运行及投资经济的中性点接地方式对于电网规划及高效运行意义重大。文中针对现有中压配电网中性点接地方式决策缺乏定量评价工具,难以综合决策的问题,提出以可靠性指标为约束条件、计及可靠性因素的全寿命周期成本最小为目标函数的决策方法,通过RBTS Bus2系统验证该决策方法的有效性。该方法综合可靠性、安全性及经济性三方面技术要求,能够保证经济性和可靠性均较理想,将为配电网中性点接地方式的规划设计提供有效的计算方法。
| [1] | 平绍勋, 周玉芳. 电力系统中性点接地方式及运行分析[M]. 北京: 中国电力出版, 2010: 118-119. |
| [2] |
苏继锋.
配电网中性点接地方式研究[J]. 电力系统保护与控制, 2013, 41(8): 143–147.
SU Jifeng. Research of neutral grounding modes in power distribution network[J]. Power System Protection and Control, 2013, 41(8): 143–147. (in Chinese) |
| [3] |
郭清滔, 吴田.
小电流接地系统故障选线方法综述[J]. 电力系统保护与控制, 2010, 38(2): 146–152.
GUO Qingtao, WU Tian. Survey of the methods to select fault line in neutral point ineffectively grounded power system[J]. Power System Protection and Control, 2010, 38(2): 146–152. DOI:10.7667/j.issn.1674-3415.2010.02.036 (in Chinese) |
| [4] |
陈民铀, 黄永, 瞿进乾.
配电网线路高阻故障识别方法[J]. 重庆大学学报, 2013, 36(9): 83–88.
CHEN Minyou, HUANG Yong, ZHAI Jinqian. High impedance fault identification method of distribution network[J]. Journal of Chongqing University, 2013, 36(9): 83–88. DOI:10.11835/j.issn.1000-582X.2013.09.013 (in Chinese) |
| [5] |
付晓奇, 徐粮珍, 赵宝丽.
10 kV配网中性点小电阻接地技术与应用[J]. 电力系统保护与控制, 2010, 38(23): 227–230.
FU Xiaoqi, XU Liangzhen, ZHAO Baoli. Discussion on the technology and application of 10 kV distribution network neutral grounding through small resistance[J]. Power System Protection and Control, 2010, 38(23): 227–230. DOI:10.7667/j.issn.1674-3415.2010.23.045 (in Chinese) |
| [6] |
戴克铭.
配电系统中性点接地方式的分析[J]. 电网技术, 2000, 24(10): 52–55.
DAI Keming. Analysis on neutral grounding of distribution system[J]. Power System Technology, 2000, 24(10): 52–55. DOI:10.3321/j.issn:1000-3673.2000.10.014 (in Chinese) |
| [7] |
贺志锋, 刘沛.
对中压配电网中性点接地方式的研究[J]. 电力自动化设备, 2002, 22(9): 70–72.
HE Zhifeng, Liu Pei. Research of neutral point grounding modes in MV distribution network[J]. Electric Power Automation Equipment, 2002, 22(9): 70–72. (in Chinese) |
| [8] |
周原, 赵立进, 康鹏.
贵州省10 kV城市配电网中性点接地方式[J]. 电网技术, 2006, 30(20): 61–64.
ZHOU Yuan, ZHAO Lijin, KANG Peng. Neutral grounding mode of urban distribution networks in guizhou province[J]. Power System Technology, 2006, 30(20): 61–64. DOI:10.3321/j.issn:1000-3673.2006.20.013 (in Chinese) |
| [9] |
赵冉, 谭伟璞, 杨以涵.
配电网中性点接地方式分析[J]. 继电器, 2007, 35(4): 22–26.
ZHAO Ran, TAN Weipu, YANG Yihan. Analysis of neutral grounding operation modes for distribution network[J]. Relay, 2007, 35(4): 22–26. (in Chinese) |
| [10] |
林志超.
中压电网系统中性点接地方式的选择与应用[J]. 高电压技术, 2004, 30(4): 60–64.
LIN Zhichao. The selection and application of neutral grounding method of MV network[J]. High Voltage Engineering, 2004, 30(4): 60–64. (in Chinese) |
| [11] |
刘明岩.
配电网中性点接地方式的选择刘明岩[J]. 电网技术, 2004, 28(16): 86–89.
LIU Mingyan. Selection of neutral grounding modes in power distribution network[J]. Power System Technology, 2004, 28(16): 86–89. DOI:10.3321/j.issn:1000-3673.2004.16.019 (in Chinese) |
| [12] |
付迎拴, 王正刚, 邝石.
中压电网接地方式的综合选取方法[J]. 电网技术, 2006, 30(15): 101–106.
FU Yingshuang, WANG Zhenggang, KUANG Shi. Medium-voltage grid grounding comprehensive selection method[J]. Power System Technology, 2006, 30(15): 101–106. DOI:10.3321/j.issn:1000-3673.2006.15.020 (in Chinese) |
| [13] |
刘艺, 聂一雄, 彭显刚, 等.
模糊推理在中性点接地方式选择中的应用研究[J]. 电力系统保护与控制, 2010, 38(7): 32–36.
LIU Yi, NIE Yixiong, PENG Xiangang, et al. Application research on the mode selection of neutral grounding with fuzzy reasoning method[J]. Power System Protection and Control, 2010, 38(7): 32–36. DOI:10.7667/j.issn.1674-3415.2010.07.007 (in Chinese) |
| [14] |
曹珍崇, 何俭声, 杨学昌, 等.
中性点接地方式对配电线路可靠性影响的区间分析[J]. 广西电力, 2007, 35(5): 5–7.
CAO Zhenchong, HE Jiansheng, YANG Xuechang, et al. Interval analysis about influence on reliability of power distribution lines with vVarious grounded neutrals[J]. Guangxi Power, 2007, 35(5): 5–7. (in Chinese) |
| [15] |
曹珍崇, 王文立, 杨学昌, 等.
中性点接地方式的加权多指标区间数灰靶决策算法[J]. 广西电力, 2007, 30(6): 1–5.
CAO Zhenchong, WANG Wenli, YANG Xuechang, et al. Decision arithmetic of neutral grounding mode based on interval multiattribute weighted grey target theory[J]. Guangxi Power, 2007, 30(6): 1–5. (in Chinese) |
| [16] |
苏海锋, 张建华, 梁志瑞, 等.
基于改进均值聚类随机粒子群算法的变电站LCC规划[J]. 电工技术学报, 2012, 27(4): 209–214.
SU Haifeng, ZHANG Jianhua, LIANG Zhirui, et al. Substation LCC planning based on refined mean clustering random particle swarm algorithm[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 209–214. (in Chinese) |
| [17] | Rosado R I J, Navarro D J A. New Multio-bjective tabu search algorithm for fuzzy optimal planning of power distribution systems[J]. IEEE Transactions on Power Systems, 2006, 21(1): 224–233. DOI:10.1109/TPWRS.2005.860946 |
| [18] |
罗晓初, 李乐, 魏志连.
全寿命周期成本理论在配电变压器改造投资决策中的应用[J]. 电网技术, 2011, 35(2): 207–210.
LUO Xiaochu, LI Le, WEI Zhilian. Applications of life cycle cost theory in decision-making of investment for distribution transformers renovation[J]. Power System Technology, 2011, 35(2): 207–210. (in Chinese) |
| [19] |
李斌, 束洪春.
基于瞬时实功率和瞬时虚功率的谐振接地系统单相接地选线新方法[J]. 电工技术学报, 2012, 27(6): 183–190.
LI Bin, SHU Hongchun. A new integration method of fault line detection in resonant earthed system based on instantaneous real power and instantaneous virtual power[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 183–190. (in Chinese) |
| [20] |
赵渊, 张煦, 林世溪, 等.
含光/柴混合发电的配电网可靠性评估模型[J]. 重庆大学学报, 2013, 36(11): 2–7.
ZHAO Yuan, ZHANG Xu, LIN Shixi, et al. A reliability evaluation model for photovoltaic/diesel hybrid power generation system[J]. Journal of Chongqing University, 2013, 36(11): 2–7. (in Chinese) |
| [21] | Billinton R, Kumar S, Chowdhury N, et al. A reliability test system for educational purposes-basic data[J]. IEEE Transactions on Power Apparatus and System, 1989, 4(3): 1238–1244. DOI:10.1109/59.32623 |
| [22] | 马士聪. 利用暂态信号的小电流接地故障距离识别技术[D]. 济南: 山东大学博士学位论文, 2008. |
| [23] |
杨永明, 王燕, 范秀君, 等.
基于灰关联-神经网络的电力工程造价估算[J]. 重庆大学学报, 2013, 36(11): 15–20.
YANG Yongming, WANG Yan, FAN Xiujun, et al. Cost estimate of power line projects based on grey relational analysis and neutral networks[J]. Journal of Chongqing University, 2013, 36(11): 15–20. DOI:10.11835/j.issn.1000-582X.2013.11.003 (in Chinese) |
| [24] | 中国电力企业联合会. 电力建设工程预算定额(第三册)[M]. 北京: 中国电力出版社, 2006. |
 2014, Vol. 37
2014, Vol. 37

