LDPC码是美国Gallager教授在1962年提出来的一种线性分组码(n,k),码长为n,信息序列长度为k,可由校验矩阵H唯一定义,H矩阵为稀疏矩阵。理论研究表明,1/2码率的LDPC码在BPSK调制下的性能距离香农极限仅差0.004 5 dB。但是,由于LDPC迭代译码算法具有较大的时间复杂度和空间复杂度,为了提高算法的执行效率,笔者采用Verilog语言以LDPC(64,32)为例描叙了整个编译码算法,最终通过FPGA综合成了硬件电路,在成本上有所降低,在速度上有了很大的提高。
1 LDPC编码 1.1 H矩阵简介H矩阵对LDPC的性能有很大的影响,一个好的H矩阵要求:1)行重、列重远小于码长;2)H矩阵中不能出现4环,即任意4个“1”相连不能是长方形;3)线性无关的列数尽量大。构造H矩阵的方法很多,如Gallager构造法[1]、单位矩阵循环移位法[1]、近似下三角矩阵构造法[2]等,本文采用π旋转矩阵构造法[3],π矩阵具有“任何一行、列以及正反对角线上均只有一个‘1’”的特性,一般采用“皇后算法”[6]实现,将此矩阵称为πA,对πA顺时针旋转90°、180°、270°可以得到πB、πC、πD,如下所示
| $ {\mathit{\boldsymbol{\pi }}_A} = \left( \begin{array}{l} 1\;\;0\;\;0\\ 0\;\;0\;\;1\\ 0\;\;1\;\;0 \end{array} \right), {\mathit{\boldsymbol{\pi }}_B} = \left( \begin{array}{l} 0\;\;0\;\;1\\ 1\;\;0\;\;0\\ 0\;\;1\;\;0 \end{array} \right), {\mathit{\boldsymbol{\pi }}_C} = \left( \begin{array}{l} 0\;\;1\;\;0\\ 1\;\;0\;\;0\\ 0\;\;0\;\;1 \end{array} \right), {\mathit{\boldsymbol{\pi }}_D} = \left( \begin{array}{l} 0\;\;1\;\;0\\ 0\;\;0\;\;1\\ 1\;\;0\;\;0 \end{array} \right), $ |
由π矩阵构造出来的H具有[Hd
| $ {{\bf{H}}^d} = \left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\pi }}_A}\;\;{\mathit{\boldsymbol{\pi }}_A}\;\;{\mathit{\boldsymbol{\pi }}_A}\;\;{\mathit{\boldsymbol{\pi }}_A}}\\ {{\mathit{\boldsymbol{\pi }}_D}\;\;{\mathit{\boldsymbol{\pi }}_A}\;\;{\mathit{\boldsymbol{\pi }}_B}\;\;{\mathit{\boldsymbol{\pi }}_C}}\\ {{\mathit{\boldsymbol{\pi }}_C}\;\;{\mathit{\boldsymbol{\pi }}_D}\;\;{\mathit{\boldsymbol{\pi }}_A}\;\;{\mathit{\boldsymbol{\pi }}_B}}\\ {{\mathit{\boldsymbol{\pi }}_B}\;\;{\mathit{\boldsymbol{\pi }}_C}\;\;{\mathit{\boldsymbol{\pi }}_D}\;\;{\mathit{\boldsymbol{\pi }}_A}} \end{array}} \right),{{\bf{H}}^p} = \left( {\begin{array}{*{20}{l}} {1\;\;0\;\;0\;\;0\;\;0\;\;0}\\ {1\;\;1\;\;0\;\;0\;\;0\;\;0}\\ {0\;\;1\;\;1\;\;0\;\;0\;\;0}\\ {0\;\;0\;\;1\;\;1\;\;0\;\;0}\\ {0\;\;0\;\;0\;\;0\;\;1\;\;1} \end{array}} \right), $ |
论文选用的π矩阵为8×8,由此构成的H矩阵为32×64。
1.2 LDPC编码Verilog描述对于信息序列Sd是已知的,设编码后的校验序列为Sp,那么系统码S=[Sd
| $ \mathit{\boldsymbol{S}}_0^p = \sum\limits_i^k {\left( {\mathit{\boldsymbol{S}}_i^d \cdot \mathit{\boldsymbol{H}}_{0, i}^d} \right)}, $ | (1) |
| $ \mathit{\boldsymbol{S}}_j^p = \mathit{\boldsymbol{S}}_{j-1}^p + \sum\limits_i^k {\left( {\mathit{\boldsymbol{S}}_i^d \cdot \mathit{\boldsymbol{H}}_{\mathit{j}, i}^d} \right)}, $ | (2) |
k为信息序列Sd的长度,之后的S1p到Sk-1p均可由如下递推得到
计算出的校验序列Sp与信息序列Sd相组合及完成了整个编码。
下面以LDPC(64,32)为例描述编码过程
Step1:初始化H矩阵,将事先通过MATLAB或者VC计算好的H矩阵存成reg型变量HD[0]=32′h80808080、HD[1]=32′h20202020…,如果H矩阵规模比较大,可以考虑生成mif文件初始化RAM,这样就需要调用IP核,两大FPGA厂家Altera和Xilinx都提供这种IP核;
Step2:当检测到START信号时,读入DATA_IN数据到databuf,且i<=0;
Step3:databuf与HD[i]相与(完成二进制乘法),所得结果再缩减异或(完成二进制累加),存入到dataout[31-i]位,硬件语言习惯将数据从最高位存起,此值作为递推初始值S0p;
Step4:i<=i+1;
Step5:databuf继续与HD[i]进行与、缩减异或操作得到newbit,Sip=Si-1p+newbit;
Step6:如果i等于32,CODE端口输出dataout的值,程序结束,否则跳转到Step4。
编码模块消耗逻辑单元250个,仿真波形如下
模块输入的为信息位,输出的为校验位,两者合并即为64比特的系统码。
2 LDPC译码LDPC译码方法有2大类:硬判决译码和软判决译码。硬判决译码是当校验方程R×HT=0不成立时,根据接收的信息和有关规则,改变一些比特的值(0或者1),然后继续验证直到方程满足或达到最大迭代次数。该判决方法用硬件比较容易实现,但性能要比软判决差,因此,目前几乎所有的LDPC译码均采用软判决方法,其中经典的算法有BP(Belief propagation algorithm)译码算法[1]和LLR BP译码算法[1]。
2.1 BP译码算法BP译码算法凭借优越的性能和合理的复杂度成为LDPC主流的译码算法,是一种建立在Tanner图上的译码方法。根据H矩阵可以绘制出表征LDPC码的Tanner图(如图 2)。
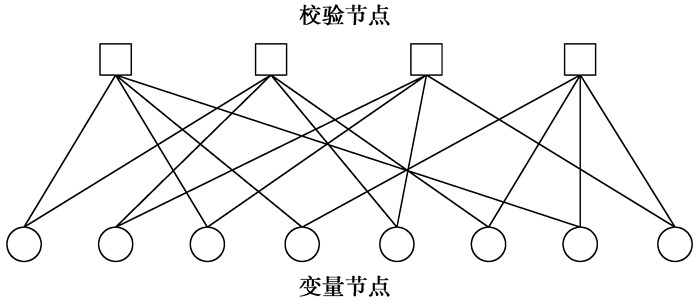
|
图 2 LDPC Tanner图 |
| $ \mathit{\boldsymbol{H}} = \left( \begin{array}{l} 1\;\;0\;\;1\;\;1\;\;0\;\;0\;\;1\;\;0\\ 1\;\;1\;\;0\;\;0\;\;1\;\;1\;\;0\;\;0\\ 0\;\;1\;\;1\;\;0\;\;1\;\;0\;\;0\;\;1\\ 0\;\;0\;\;0\;\;1\;\;0\;\;1\;\;1\;\;1 \end{array} \right), $ |
以Tanner图为基础的LDPC译码主要包括两步:变量节点消息处理和校验节点消息处理。对于收到的数据,根据信道估值计算出其条件概率P(c/r);比如接收为r,发送判断为0的概率即为P(c=0/r),发送判断为1的概率即为P(c=1/r),以此作为该变量节点的初始消息传向校验节点;校验节点将接收到的消息进行一定的运算处理后再传回变量节点;变量节点根据传回的数据连同初始信道估值数据一起运算后再传向校验节点。如此迭代下去直到变量节点满足校验方程或者达到最大迭代次数,判决输出的变量节点即为译码输出。
为了便于具体描述,引入以下符号
rji(b) (b=0,1):校验节点j传递给变量节点i的概率消息;
qij(b) (b=0,1):变量节点i传递给校验节点j的概率消息;
C(i)\j:除j外与变量节点i相连的校验节点的集合;
R(j)\i:除i外与校验节点j相连的变量节点的集合。
Step 1:计算初始消息。
根据信道模型,计算接收消息的条件概率,以AWGN(高斯白噪声信道)为例,若采用BPSK调制、信号源等概率分布的情况下,BP译码的初始消息为
| $ q_{ij}^{\left( 0 \right)} = {P_i}\left( 0 \right) = \frac{1}{{1+e-2{y_i}/{\sigma ^2}}}q_{ij}^{\left( 0 \right)}\left( 1 \right) = {P_i}\left( 1 \right) = \frac{1}{{1 + e2{y_i}/{\sigma ^2}}}, $ | (3) |
收符号yi=xi+ni,xi为发送消息符号,ni为信道噪声,服从高斯分布。Pi(0)表示接收为yi判断发送为0的概率,Pi(1)表示接收为yi判断发送为1的概率。
Step 2:计算校验节点消息。
校验节点j的消息要排除i到j这条连线,即由其他与j相连的变量节点(非i点)来决定,由此可以避免错误的传递
| $ \mathit{r}_{ji}^{\left( n \right)}\left( 0 \right) = \frac{1}{2} + \frac{1}{2}\prod\limits_{i \in R\left( j \right)\backslash i} {\left( {1-2q_{ij\backslash i}^{\left( {n-1} \right)}\left( 1 \right)} \right)}, $ | (4) |
| $ \mathit{r}_{ji}^{\left( n \right)}\left( 1 \right) = 1-r_{ji}^{\left( n \right)}\left( 0 \right) = \frac{1}{2}-\frac{1}{2}\prod\limits_{i \in R\left( j \right)\backslash i} {\left( {1-2q_{ij\backslash i}^{\left( {n - 1} \right)}\left( 1 \right)} \right)}。$ | (5) |
Step 3:计算变量节点消息。
变量节点i的消息同样要排除j到i这条线,即由其他与i相连的校验节点(非j点)来决定。
| $ q_{ij}^{\left( n \right)}\left( 0 \right) = {K_{ij}}{P_i}\left( 0 \right)\prod\limits_{j \in C\left( i \right)\backslash \mathit{j}} {r_{ji\backslash j}^{\left( n \right)}\left( 0 \right)}, $ | (6) |
| $ q_{ij}^{\left( n \right)}\left( 1 \right) = {K_{ij}}{P_i}\left( 1 \right)\prod\limits_{j \in C\left( i \right)\backslash \mathit{j}} {r_{ji\backslash j}^{\left( n \right)}\left( 1 \right)}。$ | (7) |
Kij为校正因子,确保qij(n)(0)+qij(n)(1)=1。
Step 4:判决检测。
判决类似于变量节点消息的处理,不同的是它必须将所有与变量节点i相连的校验节点的消息全部取出并运算
| $ q_i^{\left( n \right)}\left( 0 \right) = {K_i}{P_i}\left( 0 \right)\prod\limits_{j \in C\left( i \right)} {r_{ji}^{\left( n \right)}\left( 0 \right)}, $ | (8) |
| $ q_i^{\left( n \right)}\left( 1 \right) = {K_i}{P_i}\left( 1 \right)\prod\limits_{j \in C\left( i \right)} {r_{ji}^{\left( n \right)}\left( 1 \right)}。$ | (9) |
其中Ki为校正因子,确保qi(n)(0)+q(n)i(1)=1。若qi(n)(0)>qi(n)(1),则ci=0,否则ci=1。
Step 5:迭代过程。
若c×HT=0或者达到最大迭代次数则结束,否则跳转至Step 2继续迭代。
2.2 LLR BP译码算法由于每一个节点的消息都是成对存在的,因此引入对数可以减少消息传递量,同时将乘法运算变成加法运算从而降低复杂度。LLR BP译码算法步骤如下
Step 1:计算初始消息。
引入对数后,变量节点的初始消息为
| $ {L^{\left( 0 \right)}}{P_i} = \ln \frac{{q_{ij}^0\left( 0 \right)}}{{q_{ij}^{\left( 0 \right)}\left( 1 \right)}} = \ln \frac{{{P_i}\left( 0 \right)}}{{{P_i}\left( 1 \right)}} = \frac{{2{y_i}}}{{{\sigma ^2}}}, $ | (10) |
σ与yi意义均与BP算法相同。
Step 2:计算校验节点消息;
根据式(4)、(5)可得
| $ {\mathit{r}_{ji}}\left( 0 \right)-{\mathit{r}_{ji}}\left( 1 \right) = 1-2{r_{ji}}\left( 1 \right) = \prod\limits_{i \in R\left( j \right)\backslash i} {\left( {1-2{q_{ij\backslash i}}\left( 1 \right)} \right)}, $ | (11) |
由恒等式
| $ 1-2{r_{ji}}\left( 1 \right) = {\rm{tan}}\mathit{h}\left( {\frac{1}{2}\ln \left( {\frac{{{r_{ji}}\left( 0 \right)}}{{{r_{ji}}\left( 1 \right)}}} \right)} \right) = \prod\limits_{i \in R\left( j \right)\backslash i} {\tan \mathit{h}\left( {\frac{1}{2}\ln \left( {\frac{{{q_{ij\backslash i}}\left( 0 \right)}}{{{q_{ij\backslash i}}\left( 1 \right)}}} \right)} \right)}, $ |
令
则有
| $ {L^{\left( n \right)}}\left( {{r_{ij}}} \right) = 2\tan \;h-1\left( {\prod\limits_{i \in R\left( j \right)\backslash i} {\tan \mathit{h}\left( {\frac{1}{2}{L^{n-1}}\left( {{q_{ij\backslash i}}} \right)} \right)} } \right)。$ | (12) |
Step 3:计算变量节点消息。
对式(6)、(7)进行对数处理如下
| $ {L^{\left( n \right)}}\left( {{q_{ij}}} \right) = \ln \left( {\frac{{q_{ij}^{\left( n \right)}\left( 0 \right)}}{{q_{ij}^{\left( n \right)}\left( 1 \right)}}} \right) = L\left( {{P_i}} \right) + \prod\limits_{j \in C\left( i \right)\backslash j} {{L^{\left( n \right)}}\left( {{r_{ji\backslash i}}} \right), } $ | (13) |
Step 4:判决检测。
对式(8)、(9)进行对数处理如下
| $ {L^{\left( n \right)}}\left( {{q_{i}}} \right) = L\left( {{P_i}} \right) + \prod\limits_{j \in C\left( i \right)} {{L^{\left( n \right)}}\left( {{r_{ji}}} \right), } $ | (14) |
若L(n)(qi)>0,则ci=0,否则ci=1。
Step 5:迭代过程。
若c×HT=0或者达到最大迭代次数则结束,否则跳转至Step 2继续迭代。
2.3 UMP BP译码算法三角函数的计算是十分耗时的,如何简化LLR BP算法的Step 2将是提速的关键,由于tanh(x)与tanh-1(x)均为奇函数,即:tanh(x)=sgn(x)·tanh(|x|)、tanh-1(x)=sgn(x)·tanh-1(|x|),sgn(x)为符号函数,取值±1和0;则式(12)变为
| $ {L^{\left( n \right)}}\left( {{r_{ij}}} \right) = 2\left( {\prod\limits_{i \in R\left( j \right)\backslash i} {{\rm{sgn }}\left( {{L^{\left( {n-1} \right)}}\left( {{q_{ij\backslash i}}} \right)} \right)} } \right) \cdot \tan \mathit{h-}{\rm{1}}\left( {\prod\limits_{i \in R\left( j \right)\backslash i} {{\rm{tan}}\mathit{h}{\rm{ }}\left( {\frac{1}{2}\left| {L\left( {n-1} \right)\left( {{q_{ij\backslash i}}} \right)} \right|} \right)} } \right), $ | (15) |
由于0≤tanh(|x|)<1且为单调递增函数,因此有下列约等式
| $ \begin{gathered} \prod\limits_{i \in R\left( j \right)\backslash i} {{\rm{tan}}\mathit{h}{\rm{ }}\left( {\frac{1}{2}\left| {L\left( {n-1} \right)\left( {{q_{ij\backslash i}}} \right)} \right|} \right)} \approx \mathop {{\rm{min}}}\limits_{i \in R\left( j \right)\backslash i} \tan \mathit{h}\left( {\frac{1}{2}\left| {L\left( {n-1} \right)\left( {{q_{ij\backslash i}}} \right)} \right|} \right) = \hfill \\ \tan \mathit{h}\left( {\mathop {{\rm{min}}}\limits_{i \in R\left( j \right)\backslash i} \frac{1}{2}\left| {L\left( {n-1} \right)\left( {{q_{ij\backslash i}}} \right)} \right|} \right), \hfill \\ \end{gathered} $ |
则式(15)可简化为
| $ {L^{\left( n \right)}}\left( {{r_{ij}}} \right) = \prod\limits_{i \in R\left( j \right)\backslash i} {{\rm{sgn }}\left( {{L^{\left( {n-1} \right)}}\left( {{q_{ij\backslash i}}} \right)} \right)} \cdot \mathop {{\rm{min}}}\limits_{i \in R\left( j \right)\backslash i} \left| {L\left( {n-1} \right)\left( {{q_{ij\backslash i}}} \right)} \right|。$ | (16) |
UMP BP算法主要是针对LLR BP算法的Step2进行优化,经过一定的近似,省去了三角函数的累乘计算,通过比较即可完成校验节点消息的更新,仅仅牺牲少量的译码准确率换取速度的极大提升。
2.4 LDPC译码Verilog描述经过前面的理论分析,可以利用式(10)、(13)、(14)、(16)进行译码,译码过程只涉及加法运算,复杂度极低,数据均为小数,数据源为2yi/σ2,其中yi=±1,而0≤σ≤1为AWGN信道表征值,取σ=0.45(信道环境差,误码率4.2%),初始消息为±9.88。
为了便于Verilog描述,这里引入Q格式[4](定点数),数据位宽16比特,对LDPC(64,32)译码过程中的小数分析可得,其分布范围在-100~100之间,因此选用Q8格式,即最高位为符号位,中间7比特为整数,最低8比特为小数,范围-128≤X≤127.996 093 75,精度0.003 906 25。

|
Q格式与浮点数的互换公式为:Xq=(int)(Xf×2Q),Xf=(float)(Xq×2-Q),这里Q=8。运算中的负数均以补码存在(正数取反加1),以初始值为例:
由于H(32×64)矩阵比较大,L(qij)和L(rji)均与H相关联,因此需要开辟较大的存储空间,并且采用一维数组表示二维数组,如q[i][j]=q[i×COL+j],COL为矩阵列数,在FPGA中,开辟的reg类型的数组消耗的是逻辑资源LET(logic elements),而并非其内部的RAM(on chip memory),定义变量如下
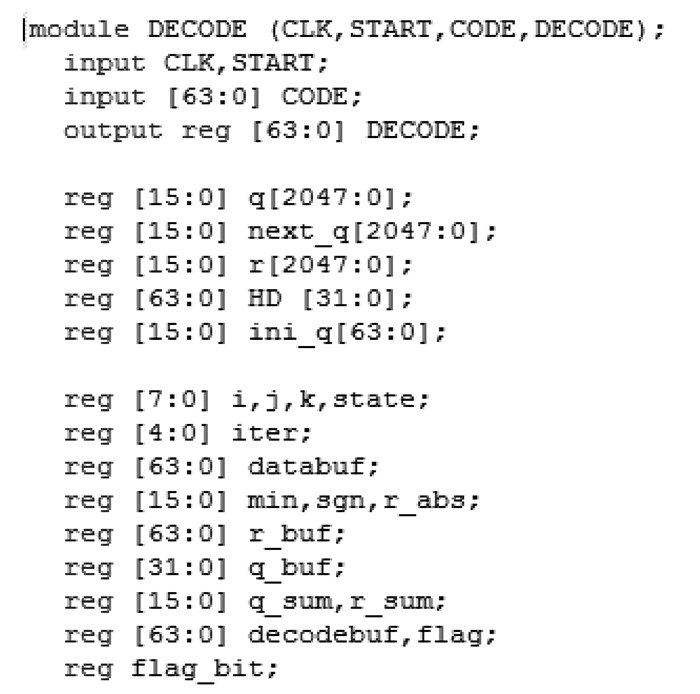
|
解决了数据表示难题后,即可按照LLR BP算法流程编写状态机程序,由于算法具有“串行”流水性,而Verilog语言是并行处理的,因此,用到了25种状态描述初始化qij、计算rji、更新qij、判决、迭代的过程。虽然整个算法是顺序执行的,但每一状态的赋值语句均是并行操作的。译码模块运用了大量的数组,消耗逻辑资源102 402个,仿真波形如下:
对照图 1和图 3,输入模块的信息位和校验位合并后人为添加随机的错误,经过译码模块后可得到正确码字。

|
图 1 编码模块仿真波形 |

|
图 3 译码模块仿真波形 |
LDPC编码过程比较简单,Verilog的并行处理将乘累加运算缩短为2个CLK节拍,整个编码过程在130个CLK节拍完成。
LDPC译码过程比较复杂,由编译报告就可以看出其消耗的资源巨大,而换来的益处就是译码速度的极大提升,以LDPC(64,32)为例,25个状态机在双重for循环的作用下进行消息的刷新和传递,迭代一次耗时64×32×25=51 200个CLK,最大迭代次数设为10,一般出错1到2比特的情况下迭代1次即可正确译码,出错3到4比特数据源迭代2到3次可正确译码,超过4比特偶尔会不能正确译码,在完全正确译码的情况下平均迭代次数为2,平均耗时102 400个CLK,FPGA系统时钟设为100 M,经计算译码平均耗时1.024 ms,数据位宽64 bit,则速率为64 Kbps。LLR BP算法收敛较快,如果数据位宽成倍数增长,传输速率也将倍增,配合更高效的调制技术,速度可进一步提升,可满足高速通信系统的要求。
笔者提出了一种用Verilog语言实现复杂算法的思想,凡是标准C语言能实现的算法,在引入Q格式(定点数)后用Verilog语言也能将之实现,对于C语言中的开方、三角函数等可以用相应的Q格式算法或者查找表等方式来实现,甚至可以引入泰勒级数近似。用Verilog编写的硬件模块其运算效能将大大高于C语言算法。
| [1] | 李少谦. LDPC码的原理与应用[M]. 北京: 国防工业出版社, 2006: 129-138. |
| [2] | 哈聪颖. LDPC码的编码实现研究[D]. 哈尔滨: 哈尔滨工业大学硕士学位论文, 2006: 21-25. http: //cdmd. cnki. com. cn/Article/CDMD-10213-2006171672. htm |
| [3] | 谢红梅. 迭代译码算法的研究[D]. 西安: 西安电子科技大学硕士学位论文, 2008: 19-24. http: //cdmd. cnki. com. cn/Article/CDMD-10701-2008056186. htm |
| [4] | 王潞钢. DSP C2000程序员高手进阶[M]. 北京: 机械工业出版社, 2005: 33-38. |
| [5] | 卢开澄, 卢华明. 组合数学[M]. 北京: 清华大学出版社, 2002. |
| [6] | 刘东华. Turbo码原理与应用技术[M]. 北京: 电子工业出版社, 2004. |
| [7] | Chen J H, Dholakia A, Eleftheriou E, et al. Reduced-complexity decoding of LDPC codes[J]. IEEE Transactions on Communications, 2009, 53(8): 1288–1299. |
| [8] | Zhang J T, Fossorier M. Shuffled iterative decoding[J]. IEEE Transactions on Communications, 2008, 53(2): 209–213. |
| [9] | Peterson W W, Weldon E J. Error correcting codes cambridge[M]. MA: MIT Press, 2010. |
| [10] | Tang H, Xu J, Kou Y, et al. On algebraic construction of Gallager and circulant low density parity check codes[J]. IEEE Transactions on Information Theory, 2004, 50(6): 1269–1279. DOI:10.1109/TIT.2004.828088 |
| [11] | Luby M G, Mitzenmacher M, Shokrollah M A, et al. Improved low-density parity-check codes using irregular graphs[J]. IEEE Transactions on Communication, 2001, 47(2): 585–598. |
| [12] | Richardson T J, Shokrollahi M, Urbanke R. Design of capacity approaching irregular low-density parity-check codes[J]. IEEE Transactions on Information Theory, 2001, 47(2): 619–637. DOI:10.1109/18.910578 |
 2014, Vol. 37
2014, Vol. 37


