2. 湖南大学 信息科学与工程学院, 长沙 410082
2. College of Information Science and Engineering, Hunan University, Changsha 410082, China
高级加密标准AES(advanced encryption standard)于2001年提出,用于取代早期DES加密算法,并逐渐成为对称密码算法中最流行的一种[1]。AES算法目前有多种实现方案,尤以软件实现方案为众。在大多数软件实现方案中,由于考虑算法是在个人电脑上运行,加密速度和加密数据的大吞吐量方面成为优先考虑的指标,并没有考虑AES密码算法在智能卡硬件实现时所需的低功耗、低资源、小面积特征[2-4]。同时,网上也有基于硬件描述语言Verilog HDL的AES代码资源,可能是因为知识产权的原因,一些关键核心代码缺少或错误,大都不能正确运行。
笔者详细叙述了AES算法的Verilog HDL硬件语言实现,特别是对具体实现过程关键核心代码进行了清晰描述,并对AES算法的实现通过模块间调用,进而实现代码的高效利用,降低芯片面积;经modelsim6.1f仿真验证正确后进行了FPGA硬件实现,
对FPGA硬件实现进行了实验结果正确性验证。模块间的重复调用可以降低AES的硬件实现面积,从而可以使得AES算法应用于目前流行的各种小面积智能卡上,给信息时代安全用卡研究提供一定参考价值[5]。
1 AES算法简介 1.1 相关定义以下定义引用于文献[1]。
定义 1 一个由b7b6b5b4b3b2b1b0组成的字节b可以表示成系数为[0, 1]的二进制多项式b7x7+b6x6+b5x5+b4x4+b3x3+b2x2+b1x+b0。
定义 2 GF(28)上的加法定义为二进制多项式加法,系数满足模2加(异或)。
定义 3 GF(28)上的乘法定义为二进制多项式乘积以8次不可约多项式为模的积,该8次不可约多项式:m(x)=x8+x4+x3+x+1。
定义 4 函数xtime定义为GF(28)上的x·b(x),若b7=0,字节b左移一位;b7=1,则字节b左移一位再“异或”“0x1B”。
定义 5 一个固定多项式a(x)=a3x3+a2x2+a1x+a0与多项式b(x)=b3x3+b2x2+b1x+b0相乘构成的运算可以用矩阵乘法表述
| $ \left( \begin{array}{l} {c_0}\\ {c_1}\\ {c_2}\\ {c_3} \end{array} \right) = \left( \begin{array}{l} {a_0}\;\;{a_3}\;\;{a_2}\;\;{a_1}\\ {a_1}\;\;{a_0}\;\;{a_3}\;\;{a_2}\\ {a_2}\;\;{a_1}\;\;{a_0}\;\;{a_3}\\ {a_3}\;\;{a_2}\;\;{a_1}\;\;{a_0} \end{array} \right)\left( \begin{array}{l} {b_0}\\ {b_1}\\ {b_2}\\ {b_3} \end{array} \right), $ | (1) |
其中,方阵是一个循环矩阵,在AES-Rijndael密码算法中,乘法算法值限于乘一个固定有逆元的多项式,从而保证乘法的可逆性。
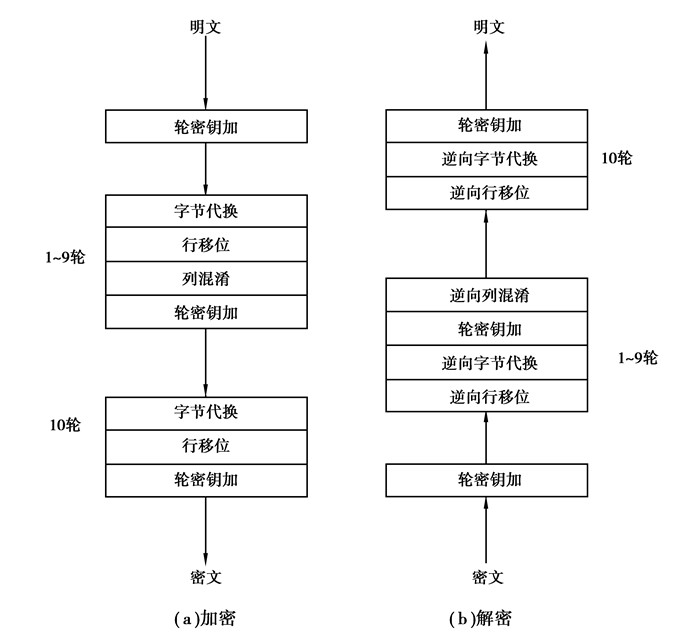
1.2 AES算法AES是一个迭代型密码算法,有128位的分组长度,三种可选密钥长度:128位、192位、256位。组成一个4行、Nb列(Nb=数据块长/32)的二维数阵列,密钥设计为4行,Nk列(Nk=密钥块长/32),算法变换的圈数Nr由Nb、Nk共同决定,其加解密运算过程如图 1。
|
图 1 AES加解密过程示意图 |
论文以密钥长度为128位为例,需要进行十轮变换,前九轮的变换过程相同,依次:字节替换、行移位、列混合和密钥加,第十轮变换跳过列混合变换。
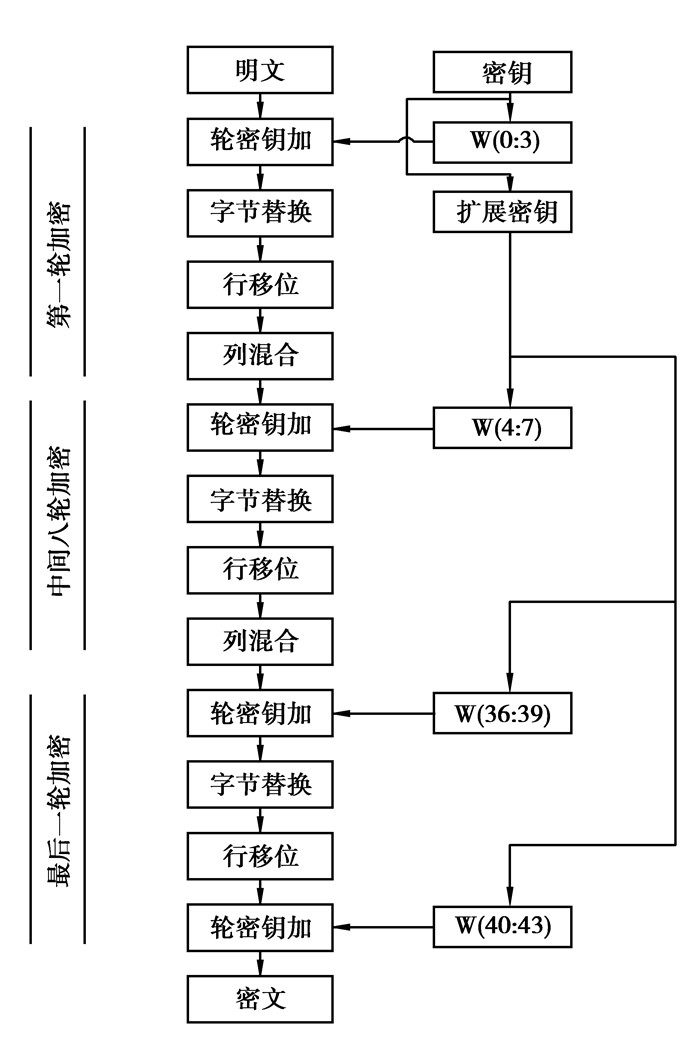
2 AES算法的Verilog HDL语言FPGA优化实现 2.1 优化方法图 2是AES算法Verilog HDL硬件描述语言实现的总体架构流程[6-7]。
|
图 2 AES原流程图 |
通过总体设计流程图可以发现,加密及解密的过程基本上是一个过程相同但方向相反的过程。虽然初始化和第10轮与中间的9轮过程有所区别,但是整个设计过程可分为字节替换,行移位,列混合与密钥扩展4个模块实现,其中密钥扩展模块将输出每轮加/解密中所需要的轮密钥,而轮密钥的调用是顺序完成的,因此十轮加/解密中所需的密钥可在其他模块执行的同时重复调用,并一次生成十轮密钥,最后通过控制模块实现轮密钥加运算。
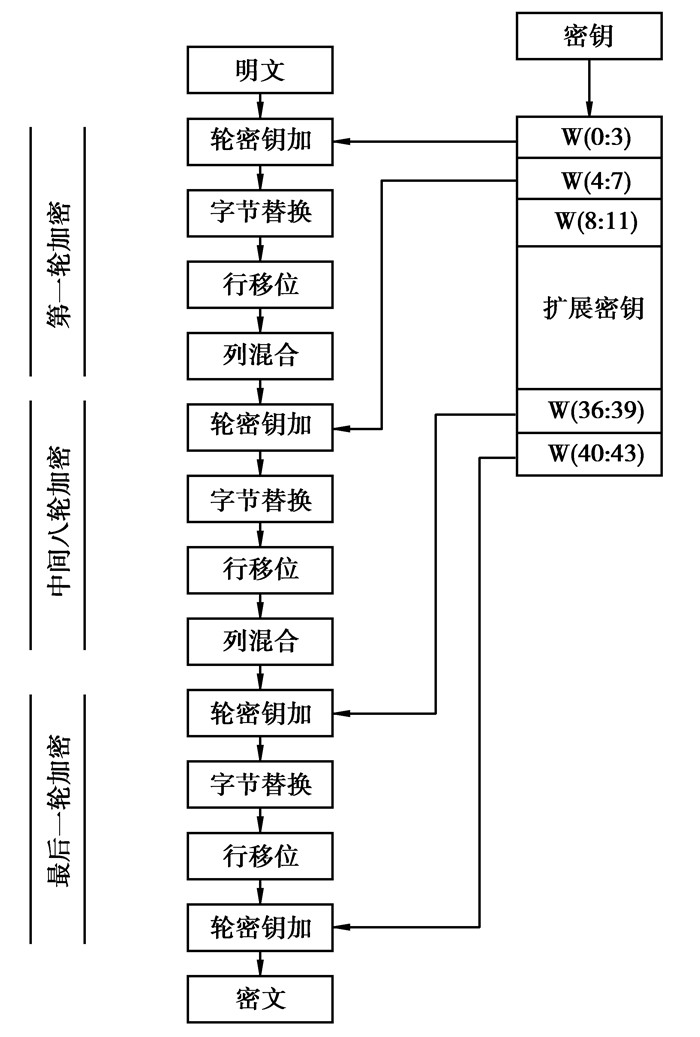
通过密钥扩展模块的重复调用,可以实现代码的高效利用,关键是节省了密码芯片的实现面积,适合于智能卡类芯片加密应用。优化后的结构流程图如图 3。
|
图 3 优化后的AES实现流程图 |
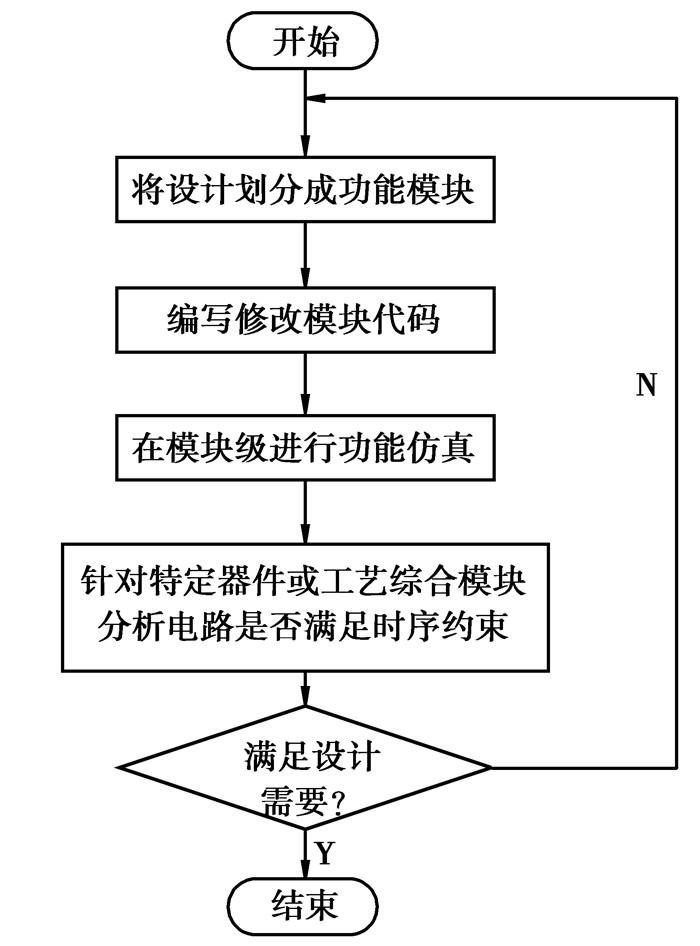
图 4为AES算法实现的具体工作流程。
|
图 4 工作流程 |
在本设计中存储的128位数用16进制表示,存储位如表 1所示。
| 表 1 存储方式示意表 |
下面的Verilog HDL语言是实现了一个查找表,s盒是一个16×16的矩阵,大小为256个字节。
always @(a)
case(a)
8′h00:d=8′h63;
8′h01:d=8′h7c;
……
8′hff:d=8′h16;
endcase
测试数据如下:
#5 a=8′h3b;
#10 a=8′h00;
#20 a=8′h26;
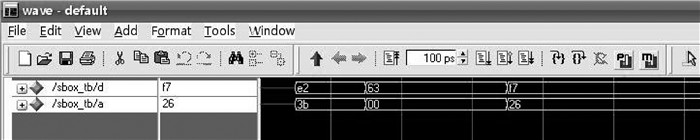
测试后的仿真波形如图 5。
|
图 5 S盒仿真波形 |
从图 4的波形分析可以看出每一个时钟信号的上升沿到来时,进行一轮变换,同时counter减1。字节变换、行移位后产生结果用aa表示送入列混合模块,产生的结果s_mix与该轮密钥进行异或操作。
2.3 列混合要实现
| $ {\mathit{\boldsymbol{S'}}_{00}} = \left( {02\;\;03\;\;01\;\;01} \right)\left( \begin{array}{l} {S_{00}}\\ {S_{10}}\\ {S_{20}}\\ {S_{30}} \end{array} \right), $ |
即
| $ {\mathit{\boldsymbol{S'}}_{00}} = \left\{ {02} \right\}\;{\mathit{\boldsymbol{S}}_{00}} \oplus \left\{ {03} \right\}\;{\mathit{\boldsymbol{S}}_{10}}{\mathit{\boldsymbol{S}}_{20}} \oplus \left\{ {01} \right\}\;{\mathit{\boldsymbol{S}}_{30}}, $ |
而02^S00可以表示为S00的移位操作(可参考定义4),用bb[1:8]代替S00,bb[1]表示S00的最高位。判断S00最高位是否为1,若为1,将S00左移一位后异或1b;若不为1,仅将S00左移一位。
详细的Verilog HDL描述代码如下
function [31:0] mix_col;
input[7:0]s0,s1,s2,s3;
reg[7:0]s0_o,s1_o,s2_o,s3_o;
begin
mix_col[31:24]=xtime(s0)^xtime(s1)^s1^s2^s3;
mix_col[23:16]=s0^xtime(s1)^xtime(s2)^s2^s3;
mix_col[15:08]=s0^s1^xtime(s2)^xtime(s3)^s3;
mix_col[07:00]=xtime(s0)^s0^s1^s2^xtime(s3);
end
endfunction
function [7:0] xtime;
input [7:0] b;xtime={b[6:0],1′b0}^(8′h1b & {8{b[7]}});
endfunction
等同于
| $ \begin{gathered} {{\mathit{\boldsymbol{S'}}}_{00}} = \left( {\left( {{\rm{S[1] = 1}}} \right)?\left( {{\mathit{\boldsymbol{S}}_{00}} \ll 1} \right)\hat 8'{\rm{h1b:}}\left( {{\mathit{\boldsymbol{S}}_{00}} \ll 1} \right)} \right) \wedge \left( {{\rm{S}}[9] = 1} \right)? \hfill \\ \left( {{\mathit{\boldsymbol{S}}_{10}} \ll 1} \right){{\hat S}_{10}}\hat 8'\mathit{h}{\rm{1}}\mathit{b}{\rm{:}}\left( {{\mathit{\boldsymbol{S}}_{10}} \ll 1} \right){{\mathit{\boldsymbol{\hat S}}}_{10}}{{\mathit{\boldsymbol{\hat S}}}_{20}}{{\mathit{\boldsymbol{\hat S}}}_3}。\hfill \\ \end{gathered} $ | (4) |
Xtime函数作用是防止溢出的发生,通过移位异或操作,可以有效的防止高位溢出。
2.4 密钥扩展每一轮的密钥都是由前一轮的密钥和本轮密钥共同产生的。
| $ {\omega _i} = {\omega _{i-4}} \oplus {\rm{Sub}}\left( {{\rm{RotByte}}\left( {{\omega _{i-1}}} \right)} \right) \oplus Rcon, $ | (5) |
| $ {\omega _{i + 1}} = {\omega _{i-3}} \oplus {\omega _i}, $ | (6) |
| $ {\omega _{i + 2}} = {\omega _{i-2}} \oplus {\omega _{i + 1}}, $ | (7) |
| $ {\omega _{i + 3}} = {\omega _{i-3}} \oplus {\omega _{i + 2}}, $ | (8) |
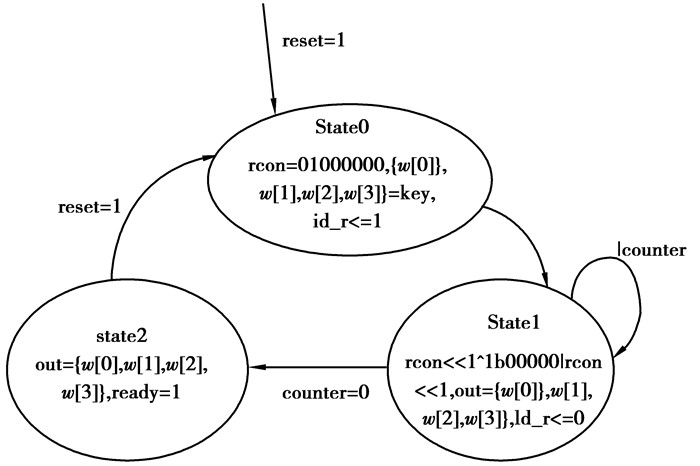
密钥扩展的状态转移图如图 6所示。
|
图 6 状态转移图 |
为实现十轮密钥同时在模块中生成,需重复调用密钥扩展模块,并将生成的十轮密钥通过计数控制依次进行轮密钥加运算。
详细的Verilog HDL描述代码如下:
always @(posedge clk)w[0]<=reset?key[1:32]:(ready?w[0]:w[0]^sub^rcon);
always@(posedge clk) w[1]<=reset?key[33:64]:(ready?w[1]:w[0]^w[1]^sub^rcon);
always@(posedge clk) w[2]<=reset?key[65:96]:
(ready?w[2]:w[0]^w[2]^w[1]^sub^rcon);
always @(posedge clk)w[3]<=reset?key[97:128]:(ready?w[3]:
w[0]^w[3]^w[2]^w[1]^sub^rcon);
always@(posedge clk)
begin
case(count2)
4′b1001:begin
outcopy[0]= {w[0],w[1],w[2],w[3]};
out<=outcopy[0];
count2<=4′b1000;
end
4′b1000:begin
outcopy[1]= {w[0],w[1],w[2],w[3]};
out<=outcopy[1];
count2<=4′b0111;
end
4′b0111:begin
outcopy[2]= {w[0],w[1],w[2],w[3]};
out<=outcopy[2];
count2<=4′b0110;
end
4′b0110:begin
outcopy[3]= {w[0],w[1],w[2],w[3]};
out<=outcopy[3];
count2<=4′b0101;
end
4′b0101:begin
outcopy[4]= {w[0],w[1],w[2],w[3]};
out<=outcopy[4];
count2<=4′b0100;
end
4′b0100:begin
outcopy[5]= {w[0],w[1],w[2],w[3]};
out<=outcopy[5];
count2<=4′b0011;
end
4′b0011:begin
outcopy[6]= {w[0],w[1],w[2],w[3]};
out<=outcopy[6];
count2<=4′b0010;
end
4′b0010:begin
outcopy[7]= {w[0],w[1],w[2],w[3]};
out<=outcopy[7];
count2<=4′b0001;
end
4′b0001:begin
outcopy[8]= {w[0],w[1],w[2],w[3]};
out<=outcopy[8];
count2<=4′b0000;
end
4′b0000:begin
outcopy[9]= {w[0],w[1],w[2],w[3]};
out<=outcopy[9];
count2<=4′b1001;
end
endcase
end
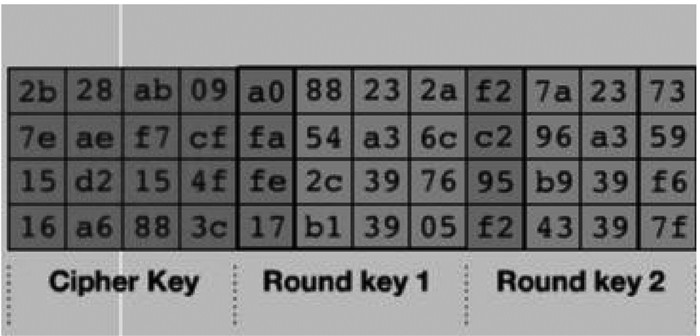
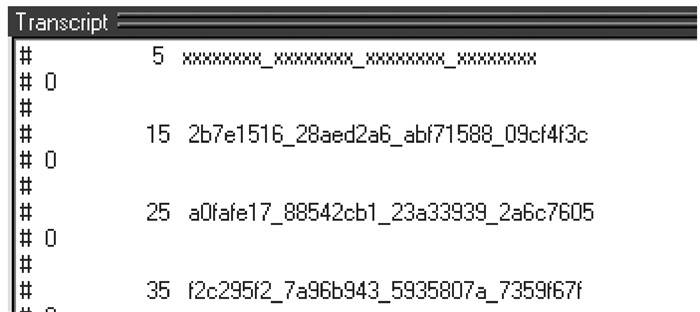
同样采取大家一般使用的测试初始密钥值(2b7e151628aed2a6abf7158809cf4f3c)进行测试代码实现正确性。得出的测试前3轮预期结果如下图 7所示,用moelsim6.1f仿真上述代码结果如图 8,其中仿真波形如图 9。
|
图 7 测试数据 |
|
图 8 命令窗口下的结果输出 |
|
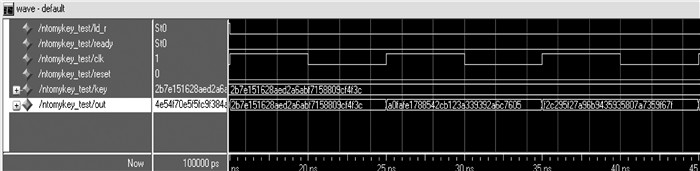
图 9 波形观察器中的结果输出 |
对图 9的波形进行分析可以发现,本模块并不设定计算轮数,由最终的顶层控制最后的运算次数,因此此处不需要初始化counter值。
1) 置初值,将初始密钥传给w[0]~w[3],ld_r信号开始设置初值0→1→0,作为一个信号量,表示key模块可以开始运行。
2) 通过异或操作产生新的密钥,同一轮的密钥同时产生。如果计数器不为0,ready信号为1,说明没有到第10轮密钥产生,保存当次产生的密钥,计数器减1,同时进入下一轮密钥扩展。
3) 计数器为0,ready信号为0,所有10轮密钥产生完毕。
其中用到的S盒查找部分由以下代码完成
sbox u0(.a(tmp_w[23:16]),d(subword[31:24]));
sbox u1(.a(tmp_w[15:08]),d(subword[23:16]));
sbox u2(.a(tmp_w[07:00]),d(subword[15:08]));
sbox u3(.a(tmp_w[31:24]),d(subword[07:00]));
2.5 FPGA实现对Verilog HDL优化实现的AES算法使用ISE9.1进行综合仿真,并最终利用EDK9.1生成位流文件后,下载到Xilinx Virtex-V FPGA板上进行硬件实现正确性的验证[10]。
实验中用于加密验证的数据如下
原文(state):3243f6a8 885a308d 313198a2 e0370734
密钥(key):2b7e1516 28aed2a6 abf71588 09cf4f3c
密文(result):3925841d 02dc09fd dc118597 196a0b32。
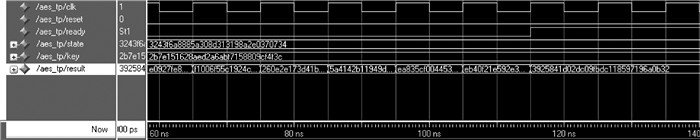
利用开发平台支持的第三方工具Modelsim 6.1f仿真结果如图 10所示
|
图 10 波形观察器中的加密输出结果图 |
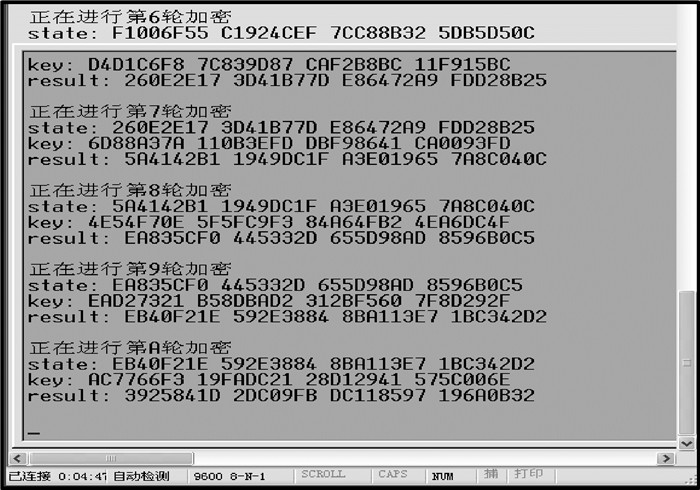
然后,在EDK环境下添加自定义IP核,为FPGA设置外部管脚,生成可以下载到目标板的硬件比特流文件;最后,通过JTAG线连接到FPGA,下载运行,通过超级终端显示运行结果。其结果如图 11所示。从实验结果图中可以得出代码描述与实现正确。
|
图 11 AES加密结果 |
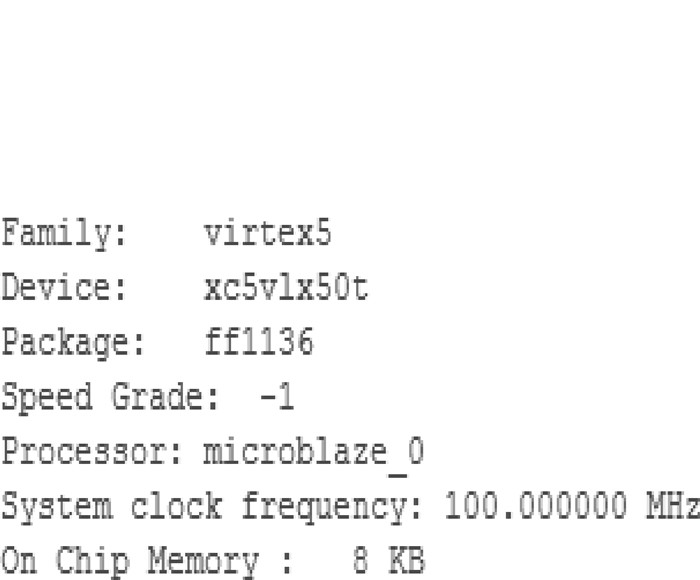
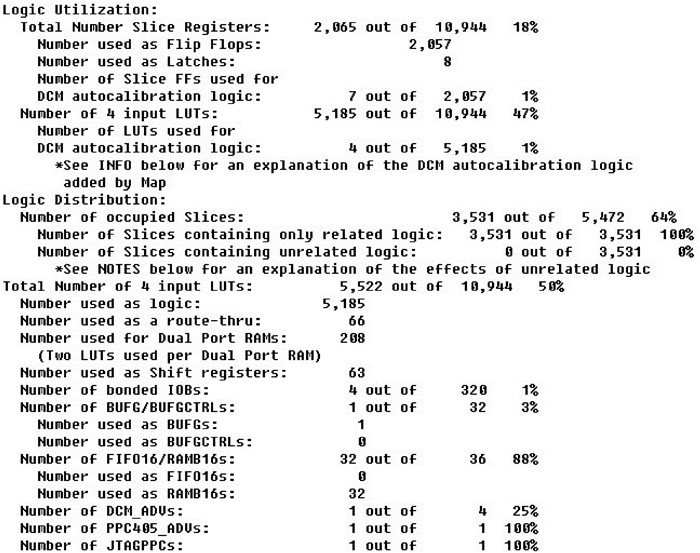
该设计在Xilinx公司的Virtex-V FPGA上综合下载实现,其硬件配置如图 12所示,主要逻辑资源的消耗情况如图 13所示,仅占用了3 531个Slice,5 522个LUT和2 057个FLIP FLOPS。同时根据图 12的时钟频率可以由公式计算加密速率为:throughput=b_length×number_of_b_sametime/latency = 128 bits/10 ns =12.8 Gb/s。,根据资源报告图 13并与同类加密算法实现所需的资源数对比[11],对比结果见表 2,进一步验证了提出的AES密码优化算法的优越性,可满足较小的芯片面积应用需求,同时加密性能仍然较高。
|
图 12 硬件配置图 |
|
图 13 优化后的AES算法FPGA下载资源报告 |
| 表 2 FPGA逻辑资源使用情况对比 |
研究对AES的Verilog HDL硬件描述语言实现进行了实验验证,对模块设计进行了优化,从而可以重复调用,用以减少AES硬件资源从而小面积实现,因此可以适应智能卡上的AES加密应用,所有代码均进行了ModelSim 6.1f验证其正确性,并用综合软件ISE9.1下载位流到FPGA上进行原型验证硬件功能正确性。
后续工作是在此基础上进行抗旁路攻击的AES密码算法Verilog HDL代码实现与FPGA硬件原型验证,从而使智能卡上的AES密码算法能够达到国标要求的抗旁路攻击安全性。
| [1] | Daemen J, Rijmen V. The design of Rijndael:AES -the advanced encryption standard[M]. Berlin: Springer, 2002. |
| [2] |
何德彪, 胡进, 陈建华.
基于FPGA的高速AES实现[J]. 华中科技大学学报:自然科学版, 2010, 38(2): 101–104.
HE Debiao, HU Jin, CHEN Jianhua. Implementation of AES-128 using FPGA[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2010, 38(2): 101–104. (in Chinese) |
| [3] |
王赜坤, 陈松涛.
一种AES密码算法的硬件实现[J]. 现代电子技术, 2010, 33(16): 10–13.
WANG Zekun, CHEN Songtao. Hardware implementation of AES cipher aalgorithm[J]. Modern Electronics Technique, 2010, 33(16): 10–13. DOI:10.3969/j.issn.1004-373X.2010.16.004 (in Chinese) |
| [4] |
叶剑, 李立新.
基于GPU的AES快速实现[J]. 计算机工程与设计, 2010, 31(2): 256–259.
YE Jian, LI Lixin. Fast implementation of AES based on GPU[J]. Computer Engineering and Design, 2010, 31(2): 256–259. (in Chinese) |
| [5] |
李浪, 李仁发, 吴克寿.
简化固定值掩码二阶差分功耗攻击方法及其防御措施[J]. 小型微型计算机系统, 2010, 31(9): 1894–1898.
LI Lang, LI Renfa, WU Keshou. Second-order differential attacking method of simple fixed-value masking and its defense measures[J]. Journal of Chinese Computer Systems, 2010, 31(9): 1894–1898. (in Chinese) |
| [6] | Zhang X M, Parhi K K. High-speed VLSI architectures for the AES algorithm[J]. IEEE Transactions on Very Large Scale IntegrationSystems, 2007, 12(9): 957–967. |
| [7] | Chung Y L, Chien C F, Hong J H, et al.An efficient area-delay product design for mixcolumns/Invmixcolumns in AES[C]//Proceedings of 2008 IEEE Computer Society Annual Symposium on VLSI.Aprial 7-9, 2007, Montpellier.Piscataway:IEEE Press, 2008:503-506. |
| [8] | Kundi D S, Aziz A, Ikram N. Resource efficient implementation of T-Boxes in AES on Virtex-5 FPGA[J]. Information Processing Letters, 2010, 110(10): 373–377. DOI:10.1016/j.ipl.2010.03.004 |
| [9] | Li Z R, Zhuang Y Q, Zhang C, et al. Low-power and area-optimized VLSI implementation of AES coprocessor for Zigbee system[J]. The Journal of China Universities of Posts and Telecommunications, 2009, 16(3): 89–94. DOI:10.1016/S1005-8885(08)60232-0 |
| [10] |
程海, 丁群, 杜辉, 等.
基于FPGA实现的SMS4算法研究[J]. 仪器仪表学报, 2011, 32(12): 2845–2850.
CHENG Hai, DING Qun, DU Hui, et al. Study of SMS4 based on of FPGA realization[J]. Chinese Journal of Scientific Instrument, 2011, 32(12): 2845–2850. (in Chinese) |
| [11] |
黄前山, 季晓勇.
基于低成本FPGA的AES密码算法设计[J]. 通信技术, 2010, 43(9): 156–158.
HUANG Qianshan, JI Xiaoyong. Design of AES encryption algorithm based on low-cost FPGA[J]. Communications Technology, 2010, 43(9): 156–158. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

