2. 重庆通信学院 信息工程系, 重庆 400035
2. Department of Information Engineering, Chongqing Communication Institute, Chongqing 400035, China
随着网络和计算机技术飞速发展,网上图像传输给人们提供了很大便利,但是在网络应急通信情况下,海量的图像数据安全存储和传输问题日益突出。对于一些涉密的、隐私的、高价值的和不宜公开传输的图像,需要高效、安全地传输或存储。这就需要图像的压缩和加密技术[1]。同时由于受设备、场地等条件限制、实时传输等要求及已有压缩加密算法存在的不足的制约,需要研究新的压缩与加密同步的技术[2-4]。如果将图像先加密、再压缩,由于加密破坏了其空间和时间相关性,使压缩变得不可能或压缩率低,不能满足实际应用的需要。如果将图像先压缩、再加密,则传统加密方法又不太适合,并且也不能满足实际应用的需要。鉴于此,对数字图像需要设计压缩和加密同时进行且计算复杂度低的算法。因此,为了满足图像传输效率和安全性的要求,数字图像或视频加密和压缩结合的技术成为了当前国内外研究的热点[5-9]。
当前,对图像加密和压缩研究的文献不少[1-9]。文献[10]较早做了在DCT变换域中实现图像加密压缩的工作,但出现加密后的系数不在原始系数的取值区间,无法简单地用诸如异或运算等方式实现加密。文献[11]解决了加密前后系数区间的问题,但效率较低,并且使用一维混沌序列的加密强度比较低,容易被破坏者解密。文献[12]中,提到的CWW算法对所有小波系数进行置乱,使得高低频系数之间发生迁移,严重影响编码效率,还会造成量化误差,影响解码质量。这些传统的结合方法都是将加密和压缩分开进行的,目前缺少一种将加密和压缩同步进行的方案。文献[13]引进多路复用和光学相关的思想,在DCT域同时完成了图像加密和压缩,取得了比较好的效果。
受文献[2]和[4]的启发,借鉴图像压缩和加密同时进行的思想和多路复用的思想,基于混沌系统和小波变换,对文献[13]的方法进行了改进,得到了一种图像压缩加密同步方案。首先对4幅原始图像进行小波变换操作,将每幅图像变换域中低频分量(LL)提取出来,按顺序构成一个二维系数矩阵;然后对该二维系数矩阵采用混沌方法进行加密,接着将置乱后的矩阵按顺序还原回4个二维系数矩阵;最后经小波逆变换得到加密压缩图像。该改进方案不仅实现图像加密和压缩同步进行,而且还增强了加密的安全性,并提高了图像的压缩率。
1 混沌序列混沌现象是在非线性动力系统中出现的确定性的,类似随机的过程。这种过程既非周期,又不收敛,并且对初始值有极其敏感的依赖性[14]。
| $ {x_{k + 1}} = f({{x}_k}), $ | (1) |
其中,xk∈v=(0,1),k=0,1,2,3,…,称之为状态。而f:v→v是一个映射,将当前状态映射xk到下一个状态xk+1如果由初始值x0开始,反复应用f,就得到一个序列{xk,k=0,1,2,3,…,}这一序列称为该离散时间动力系统的一条轨迹。
一类非常简单却被广泛研究的动力系统是 Logistic 映射,其定义如下
| $ {x_{k + 1}} = u{x_k}(1 - {{x}_k}), $ | (2) |
其中,0≤u≤4称为分枝参数,xk∈(0,1)。当3.569 945 6≤u≤4时,Logistic 映射工作处于混沌状态。也就是说,由初始条件x0在 Logistic 映射的作用下所产生的序列{xk,k=0,1,2,3,…,}是非周期的、不收敛的,且对初始值非常敏感。Logistic 序列的这些特性表明,应用其进行图像加密将具有高的安全性能[10]。
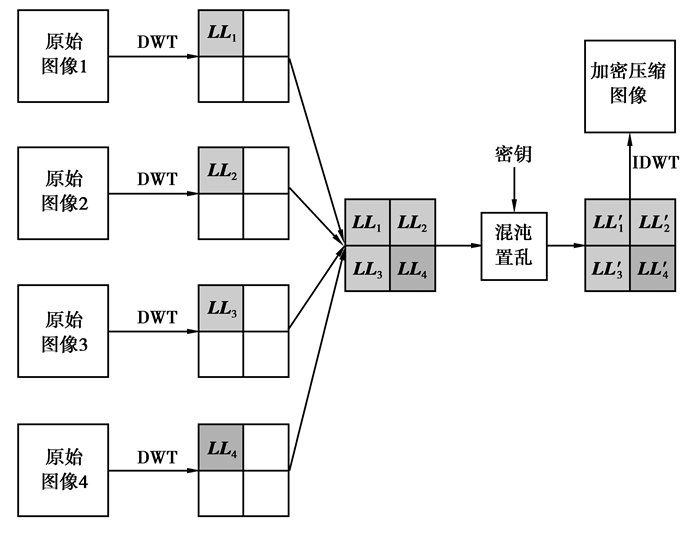
2 算法思想及算法步骤由于原始图像的绝大部分能量集中在小波变换后的低频成分(LL)部分,只需要低频成分就能够重构与原始图像非常相似的图像,因此改进的算法只针对小波系数矩阵中的低频分量进行加密。使用该方法,很大程度上避免了高低频系数迁移而引起图像原始信息的丢失。将4幅同样大小的原始图像进行小波变换,对变换后的LL成分按图 1的方式组合得到二维系数矩阵。根据混沌序列,对该二维系数矩阵进行混沌置乱加密。再将置乱后的二维矩阵重新按顺序组合得到4个二维小波系数矩阵,进行小波逆变换得到加密压缩图像。这样,将4幅图像融合加密到一幅图像中,达到了压缩效果,并且还原效果理想。
改进的加密压缩新方案流程如图 1所示。
|
图 1 加密压缩流程图 |
设4幅相同尺寸的原始灰度图像分别为Im×n(1)、Im×n(2)、Im×n(3)和Im×n(4),如果4幅图像尺寸不相同,可通过对行像素或列像素补0或其他值,使得4幅图像尺寸相同。设加密压缩后图像为I’m×n,加密压缩算法步骤如下
Step 1 读取原始4幅灰度图像Im×n(1)、Im×n(2)、Im×n(3)和Im×n(4),分别对4幅图像进行小波变换(实验中可选用“db1”小波),选取4幅图像变换后的低频成分LL1、LL2、LL3、LL4,按照图 1中显示的方式组成二维系数矩阵Ck×l。其中,k=m,l=n。
Step 2 Logistic 混沌序列置乱
根据式(2) Logistic 迭代方程计算得到二维 Logistic 混沌映射,分别记为x和y,表示如下
x={xi|i=1,2,…,k×l},
y={yj|j=1,2,…,k×l},
其中u1=0.89,u2=0.89,x1 =0.99,y1 =0.02。
利用x,y对Ck×l的值进行位置置乱,即将像素位置(i,j)的值与像素位置(a,b)的值进行互换,得到C′k×l。
| $ \begin{array}{l} {{\mathit{\boldsymbol{C'}}}_{k \times l}} = \{ \mathit{C'}{\rm{(}}\mathit{i, j}{\rm{)}}\left| {i = 1, 2, \cdot \cdot \cdot, k;j} \right. = 1, 2, \cdot \cdot \cdot, l\}, \\ \mathit{\boldsymbol{a = }}\left\lfloor {{x_i} \times m} \right\rfloor + 1, \\ \mathit{\boldsymbol{b = }}\left\lfloor {{y_i} \times n} \right\rfloor + 1, \end{array} $ |
其中k,l为Ck×l矩阵行、列数,
Step 3 将C′k×l分别按LL1、LL2、LL3、LL4相同的尺寸分解成4个二维系数矩阵LL′1、LL′2、LL′3、LL′4,再分别对它们进行小波逆变换,得到加密压缩后图像I′m×n。
Step 4 需注意由于置乱加密后的系数经小波逆变换后取值区间不在[0, 255]区间内,这样存储后的图像再次读取时会发生变化,不能还原原始图像。为保证还原效果,在存储前应进行映射处理,将加密后图像的像素值映射至[0, 255]区间内。映射按下面式(3) 进行,便得到融合加密后的图像I″m×n。
| $ {{I''}_{m \times n}}({i, j}) = \frac{{{{I'}_{m \times n}}({i, j}) - {p_{\min }}}}{{{p_{\max }} - {p_{\min }}}} \times 255, i = 1, 2, \cdot \cdot \cdot, k;j = 1, 2, \cdot \cdot \cdot, l, $ | (3) |
其中pmin是I′m×n中最小的灰度值,pmax是I′m×n中最大的灰度值。
Step 5 解密是上述过程的逆过程。解密时要将 Logistic 混沌序列的初始值和系数,以及pmin和pmax作为密钥传给接收方,解密时再按式(4) 逆映射灰度值,接着进行小波变换和混沌解密反置乱,就可以还原4幅原始图像的低频数据。再把每个4幅原始图像低频分量之外的小波系数补0,再进行小波逆变换就能还原得到4幅原始图像。
| $ {{{\tilde I'}}_{m \times n}}({i, j}) = ({p_{\max }} - {p_{\min }}) \times {{{\tilde I}}_{m \times n}}({i, j})/255 + {p_{\min }}, i = 1, 2 \cdot \cdot \cdot, k;j =\\ 1, 2, \cdot \cdot \cdot, l, $ | (4) |
其中
为验证改进算法的有效性,通过以大小为256×256的幅测试图像为例,采用MATLAB7.4.0 (R2007a)进行仿真实验。Logistic 混沌系统中取u1=0.89;u2=0.89;x1=0.99;y1=0.02,此即为加密时的密钥。
3.1 主观效果分别将加密压缩后的图像保存为BMP和JPG格式进行还原,其加密压缩效果如图 2(b)和图 3(b)所示。

|
图 2 存储为JPG图像的加密压缩效果图 |

|
图 3 存储为BMP图像的加密压缩效果图 |
从图 2和图 3中,可以看出改进的压缩加密算法,能够很好地还原出原始图像,得到了较好的加密效果。计算和观察得知,还原图像的质量比原始图像的质量有所下降,但质量下降没有影响图像的理解,视觉效果也在可接受的范围内。因此,改进的算法可应用于图像的安全通信领域。
3.2 置乱度图像被置乱或加密的程度用置乱度(SM)用来评估,它能较为客观地反映图像的加密效果。目前,国内外许多研究者都给出了置乱度的定义,却又各不相同。引用文献[15]中定义的置乱度来评估图像的加密程度,其置乱度定义为
| $ {\rm{SM(}}{I, I'}{\rm{) = }}\frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{({{I}_{ij}} - {{I'}_{ij}})}^2}} } }}{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{({{I}_{ij}} - {R_{ij}})}^2}} } }}, $ | (5) |
其中,I={Iij}M×N表示原始图像,I′={I′ij}M×N表示置乱或加密图像,R={Rij}M×N表示与原始图像相同大小的均匀分布噪声图像。为了使得加密图像的置乱度具有可比性,通常采用同一幅均匀分布的噪声图像。将加密压缩后得到的图像与4幅原始图像进行比较,得到的实验结果如表 1。
| 表 1 加密后图像的置乱度 |
从表 1可以看出,在JPG压缩因子为100时,存储为bmp和JPG格式后,加密压缩图像的置乱度都大于0.52,置乱效果较好。实验中只使用了1次混沌序列置乱加密,为了提高安全性可以多次重复置乱加密。
3.3 压缩率压缩率作为图像压缩的一个评价指标,其计算式记为
| $ 压缩率 = \frac{{原始图象大小 - 压缩后图象大小}}{{原始图象大小}} \times 100\%, $ | (6) |
在压缩率测试中,与传统加密压缩算法大都经历压缩编码不同,算法未经压缩编码就获得了压缩效果。采用尺寸均为256×256像素的4幅原始BMP图像(总的大小为4×65=260kbyte)进行测试,并将加密压缩后图像存储为JPG格式,进行压缩率的比较。经过加密压缩后得到压缩率如表 2所示。
| 表 2 压缩效率比较 |
可以看出,由于算法借鉴“多路复用”的思想,其优势是在JPG压缩前已将4幅原始图像压缩到1幅图像中,实现了一次图像尺寸的压缩。同时,改进的算法不仅实现了图像加密,而且在加密的同时实现了图像的压缩,并且从表 2可以看出,压缩率比直接压缩的压缩率增加了7.92个百分点。
4 结语改进的一种基于混沌和小波变换的图像加密压缩算法,实现了对加密和压缩同时进行处理。通过在小波变换域中使用混沌序列置乱加密,得到加密效果较好的加密压缩图像。算法借鉴“多路复用”的思想,达到较好的压缩效果,使得压缩率有较大提高。仿真实验结果,说明了加密和压缩同时处理的方法的性能良好。
| [1] | Yuen C H, Wong K W. A chaos-based joint image compression and encryption scheme using DCT and SHA-1[J]. Applied Soft Computing, 2011, 11(8): 5092–5098. DOI:10.1016/j.asoc.2011.05.050 |
| [2] | Alfalou A, Brosseau C, Abdallah N, et al. Simultaneous fusion, compression, and encryption of multiple images[J]. Optics Express, 2011, 19(24): 24023–24029. DOI:10.1364/OE.19.024023 |
| [3] | Alfalou A, Elbouz M, Jridi M, et al.A new simultaneous compression & encryption method for images suitable to recognize form by optical correlation[C]//Proceedings of Optics and Photonics for Counterterrorism and Crime Fighting, September 24, 2009, Berlin, Germany.[S.l.]:SPIE, 2009:7486. https://hal.archives-ouvertes.fr/hal-00579175/document |
| [4] | Li X B, Knipe J, Cheng H. Image compression and encryption using tree structures[J]. Pattern Recognition Letters, 1997, 18(11-13): 1253–1259. DOI:10.1016/S0167-8655(97)00099-8 |
| [5] | Ou S C, Chung H Y, Sung W T. Improving the compression and encryption of images using FPGA-based cryptosystems[J]. Multimedia Tools and Applications, 2006, 28(1): 5–22. DOI:10.1007/s11042-006-5117-6 |
| [6] | Chang H T, Lin C C. Intersecured joint image compression with encryption purpose based on fractal mating coding[J]. Optical Engineering, 2007, 46(3): 1–11. |
| [7] | Razzaque A, Thakur N V. An approach to image compression and encryption[J]. International Journal of Image Processing and Vision Sciences, 2012, 1(2): 52–55. |
| [8] |
张萌, 刘忠信, 孙青林, 等.
基于混沌的视频加密与压缩方法研究[J]. 控制工程, 2005, 12(5): 482–485.
ZHANG Meng, LIU Zhongxin, SUN Qinglin, et al. Chaos based video compression and encryption algorithms[J]. Control Engineering of China, 2005, 12(5): 482–485. (in Chinese) |
| [9] | Pande A, Zambreno J, Mohapatra P.Joint video compression and encryption using arithmetic coding and chaos[C]//Proceedings of the 20114th International Conference on Internet Multimedia Services Architecture and Application, December 15-17, 2010, Bangalore.Piscataway:IEEE Press, 2010:1-6. |
| [10] |
孙鑫, 易开祥, 孙优贤.
基于混沌系统的图像加密算法[J]. 计算机辅助设计与图形学学报, 2002, 14(2): 136–139.
SUN Xin, Yi Kaixiang, Sun Youxian. New image encryption algorithm based on chaos system[J]. Journal of Computer-Aided Design & Computer Graphics, 2002, 14(2): 136–139. (in Chinese) |
| [11] |
彭成, 柳林.
基于混沌序列的压缩图像加密算法[J]. 计算机工程, 2008, 34(20): 177–179.
PENG Cheng, LIU Lin. Encryption algorithm for compressed images based on chaotic sequences[J]. Computer Engineering, 2008, 34(20): 177–179. DOI:10.3969/j.issn.1000-3428.2008.20.065 (in Chinese) |
| [12] |
平亮, 孙军, 周军.
一种基于JEPG2000标准的数字图像加密算法[J]. 电视技术, 2006, 7(1): 87–90.
PING liang, SUN jun, ZHOU jun. An Algorithm for image encryption based on JPEG2000[J]. Video Engineering, 2006, 7(1): 87–90. (in Chinese) |
| [13] | Loussert A, Alfalou A, Sawda E R, et al. Enhanced system for image's compression and encryption by addition of biometric characteristics[J]. International Journal of Software Engineering and Its Applications, 2008, 2(2): 111–118. |
| [14] |
陈巧琳, 廖晓峰, 陈勇, 等.
改进的基于混沌序列的幻方变换图像加密[J]. 计算机工程与应用, 2005, 22(5): 138–139.
CHEN Qiaolin, LIAO Xiaofeng, CHEN Yong, et al. Modified image encryption based on chaotic sequences and rubik cube transformation[J]. Computer Engineering and Applications, 2005, 22(5): 138–139. (in Chinese) |
| [15] |
侯启槟, 杨小帆, 王阳生, 等.
一种基于小波变换和骑士巡游的图像置乱算[J]. 计算机研究与发展, 2004, 41(2): 369–375.
HOU Qibin, YANG Xiaofan, WANG Yangsheng, et al. An image scrambling algorithm based on wavelet transform and knight's tour[J]. Journal of Computer Research and Development, 2004, 41(2): 369–375. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


