随着物联网[1-2](Internet of Things, IoT)的发展及其衍生技术在各个领域的普及和推广,越来越多用于物联网的技术和标准相继提出。物联网已经得到了包括医疗服务提供商、医院、政府、研究学者以及工业界各方人士的广泛关注[3]。与此同时,物联网中越来越多的安全问题也逐渐暴露出来。目前,国内外针对物联网安全研究[4-5]主要有攻击检测、密钥机制、数据融合、定位技术、安全协议等几个方面。
由于物联网通信节点本身存在着内存与电量不足等缺陷,现有的安全防御方法难以应用到物联网中。针对这一现状,国内外专家提出了多种不同的入侵检测技术[6-12]以实现对物联网的安全防护, 其中结合博弈论的思想所构建的入侵检测主动防御模型[13-15]是一种较好的解决方法,比较符合实际的网络防御策略。在文献[16] AGAH等提出的基于博弈理论的入侵检测系统(intrusion detection system, IDS)在一定程度上解决了该问题,但是他们构建的模型只能针对单个节点或簇头节点进行防御,并且需要提前对节点行为进行预判才能实现实际的检测效果。针对这些不足,文献[1]提出一种重复博弈论入侵检测模型,通过多次博弈过程,攻防双方不断地学习采取有效的策略并且结合随机最优反应均衡算法,使该模型最终会趋于纳什均衡,以实现检测恶意节点的采取攻击策略的目的。在每次博弈过程中,如果检测到恶意节点的攻击,就会将该节点的数据包丢失,因此为了保障整个网络的效率以及发包成功率,在该模型算法中引入通用惩罚策略[18]对恶意节点采取一定时隙的惩罚策略,降低恶意节点的攻击概率,以保障网络整体的发包成功率提高网络效率。最后通过实验仿真验证该模型的可行性。
1 传统博弈模型建立AGAH等[16]提出的基于博弈理论的入侵检测系统,通过观察攻击者行为来决定保护哪个通信节点或簇头节点,如果入侵检测系统正好保护的是攻击者攻击的通信节点或簇头节点,则这次攻击就是失败的,IDS能获得很高的收益,反之,则这次攻击是成功的,攻击者将获得较高的收益。具体思想是通过构建攻击者攻击策略空间SA=(Sak, Snak, Sao),IDS防御策略空间SD=(Sdk, Sdo),其中在攻击者攻击策略空间中Sak表示攻击者攻击通信节点或簇头节点K,Snak表示攻击者不攻击通信节点或簇头节点K,Sao表示攻击者攻击其他通信节点或簇头节点;在IDS防御策略空间中,Sdk表示防御通信节点或簇头节点K,Sdo表示防御其他的通信节点或簇头节点K。并且在引入博弈双方利益因子如表 1所示。
| 表 1 博弈双方利益因子 |
博弈双方的收益矩阵为
| $ A = \left[\begin{array}{l} {a_{11\;\;\;}}{a_{12}}\\ {a_{21}}\;\;\;{a_{22}}\\ {a_{31\;\;}}\;{a_{32}} \end{array} \right], $ | (1) |
| $ D = \left[\begin{array}{l} {d_{11}}\;\;{d_{12}}\\ {d_{21}}\;\;{d_{22}}\\ {d_{31}}\;\;{d_{32}} \end{array} \right]。$ | (2) |
将博弈双方利益因子代入式(1) 与式(2) 中可以得出
| $ A = \left[\begin{array}{l} \;\;\;U({t})-{{C}_k}\;\;\;\;\;\;\;\;\;\;\;\;U({t})-{{C}_{k'}}-\sum\limits_{i = 1}^{{N_k}} {{A_{{\rm{L}}{k}}}} \\ \;\;\;U({t}) - {{C}_k}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;U({t}) - {{C}_{k'}}\\ U({t}) - {{C}_k} - \sum\limits_{i = 1}^{{N_{k'}}} {{A_{{\rm{L}}{k'}}}\;\;U({t}) - {{C}_{k'}} - \sum\limits_{i = 1}^{{N_{k'}}} {{A_{{\rm{L}}{k'}}}} \;} \end{array} \right], $ | (3) |
| $ {D = }\left[\begin{array}{l} {P_{\rm{I}}}({t})-{C_{\rm{I}}}\;\;{P_{\rm{I}}}({t})-{C_{\rm{I}}}\\ \;\;\;{C_{{\rm{W}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}{C_{\rm{W}}}\\ {P_{\rm{I}}}({t})-{C_{\rm{I}}}\;\;{P_{\rm{I}}}({t}) - {C_{\rm{I}}} \end{array} \right]。$ | (4) |
从式(3)与式(4)2个收益矩阵,得到这个模型的纳什均衡为(Sak, Sdk),即当攻击者攻击通信节点或簇头节点K时,IDS防御的也是通信节点或簇头节点K,此时入侵检测系统能够较好地对恶意节点的攻击进行拦截,达到保护网络的目的。同时,从此模型也可以看出攻击者是被鼓励攻击的。
但是,该系统模型主要是基于一次博弈理论,不适用于投入到现实网络中使用,其中最重要的一点是,在现实网络中,博弈双方不可能只进行一次博弈,因此为了更好地适应现实网络,需要对此模型进行适当的优化。
2 优化模型 2.1 建立重复博弈模型在上述模型基础上提出重复博弈防御模型(repeated game defend model, RDM),可以用一个四元组表示,其表达式为
| $ {R_{{\rm{RDM}}}} = ({\rm{Attender}},{\rm{Action}},{\rm{Profits,Times}}), $ | (5) |
式中:Attender包含攻击者与IDS分别用a和d表示,不同的参与者,其采取的行动空间不同,攻击者的行动空间为Aa=(N, A, M, P),分别代表正常、攻击、错误、预攻击;而IDS的行动空间为Ad=(C, R, W, D),即分别代表继续执行、推荐执行、警告、防御。双方的收益函数用Ua(Aa)与Ud(Ad)表示,T表示博弈次数。将式(5) 转化为
| $ {R_{{\rm{RDM}}}} = ({a, d}{\rm{;}}{{A}_a}, {{A}_d};{{U}_a}({{A}_a}), {{U}_d}({{A}_d});{T})。$ | (6) |
在式(6) 的基础上,可以构建RDM的攻击策略集合与IDS防御策略集合,分别表示为
| $ {S_a} = ({{S}_N}, {{S}_M}, {{S}_P}, {{S}_A}), $ | (7) |
| $ {S_d} = ({S_C}, {S_R}, {S_W}, {S_D})。$ | (8) |
并且用Sad=(sa, sd|sa∈Sa, sd∈Sd)表示一次博弈双方采取的行动策略。
根据上述理论可知,当Sad=(SA, SC)时,攻击者获得利益最高,而当Sad=(SP, SD)时,IDS获得效益最高,即就是攻击者攻击时,IDS采取放行的策略最有利于攻击者,而在攻击者准备攻击时,IDS就采取防御策略最有利于IDS,根据这个原理,可以将攻击者和IDS行动策略所组成的集合转化为相应的偏好集,攻击者偏好集可以表示为
| $ \begin{array}{l} {P_D} \prec {M_D} \sim {P_W} \prec {P_R} \sim {M_W} \prec MR \sim AR \prec \\ {A_W} \sim {N_D} \prec {A_D} \sim {N_W} \prec {N_R} \prec {M_C} \prec {P_C} \prec {N_C} \prec {A_C}, \end{array} $ | (9) |
IDS偏好集可以表示为
| $ \begin{array}{l} {A_C} \prec {P_C} \prec {N_D} \prec {M_C} \prec {N_W} \prec {N_R} \prec {M_R} \prec \\ {M_W} \prec {P_R} \prec {P_W} \prec {A_R} \prec {A_W} \prec {M_D} \prec {P_D} \prec {A_S} \prec {N_C}, \end{array} $ | (10) |
式中,
| $ {U}{\rm{(}}{X}{\rm{) = }}{{P}_1}u({{x}_1}) + {{P}_2}u({{x}_2}) + \cdot \cdot \cdot + {P_k}u({{x}_k}), $ | (11) |
最终求出该偏好集的效用值即博弈双方能获得的效益函数值。式(11) 能在理想的概率情况下即攻防双方都采取平均概率,采取各组行动策略的概率为0.25时,可以求出此博弈模型的收益矩阵,并且最终算出该模型的纳什均衡。
2.2 引入随机最优反应均衡算法为使得上述概率Pi的值更适用于实际网络,即攻防双方采取各个行动策略的概率不可能都为0.25,因此引入了随机最优反应均衡算法调整概率Pi的取值,使模型更适用于实际网络情况。即如果存在概率P*∈Δ, 使得Pi*=σi(ui(P*)),则称P*=(P1*, P2*, …, Pi*)是RMD的一个随机最优反应均衡解。
Pi*表示攻击者或IDS某次博弈中采取某种策略的概率,
| $ {\rm{\pi }}_i^* = \frac{{{\rm{e\lambda }}{ui}{\rm{(}}{{\rm{\pi }}^*}{\rm{)}}}}{{\sum\limits_{k = 1}^i {{\rm{e\lambda }}{ui}{\rm{(}}{{\rm{\pi }}^*}{\rm{)}}} }}。$ | (12) |
当λ→∞时,随机最优反应均衡会趋向于纳什均衡。也就是式(11) 所能求得的最终结果。
同理正常的网络环境中不会出现这么理想的概率,并且每次攻击者会采取不同的策略攻击手段来不断完善自己的攻击,为了更加精确地检测攻击者的入侵策略,对式(11) 和式(12),做进一步优化,以得出更加符合实际的入侵检测模型,其中主要是对随机最优反应均衡解中概率做出更加精确的描述。
在式(11) 和式(12) 的基础上,引入贴现因子δ,δ∈[0, 1],以便求得在随机最优反应均衡中更加精确的概率函数。
贴现因子的主要作用是对每次博弈双方所获得的收益做综合度量,即δ的值越大,表示攻击者或IDS更加注重整体的收益,反正则是注重局部的收益,达攻击者或IDS的收益函数可表示为
| $ {U_i}({ad}) = \sum\nolimits_{k = 1}^\infty {{\delta ^{k - 1}}{U_i}({X})} 。$ | (13) |
同时,IDS不可能在第一次就检测出攻击者,所以综合考虑检测到攻击者的概率问题,采用随机概率方式即Pi = (1-πi*)k-1πi*,即IDS在攻击者攻击了k次之后才检测到攻击者,因此攻击者或IDS的每次博弈收益函数为
| $ {U_i} = \sum\limits_{k = 1}^\infty {{{(1 - {\rm{\pi }}_i^*)}^{k - 1}}{\rm{\pi }}_i^*{\delta ^{k - 1}}{U_i}({X})} 。$ | (14) |
在式(14) 所描述的收益函数中,博弈双方会在每次博弈中动态调整自己的行动策略的概率,以追求最大的收益值,因此可以根据此思想有效检测恶意节点的攻击行为,并且在检测出恶意节点的攻击行为后将该节点的所有数据包都丢弃,达到的网络的安全防护。
2.3 通用惩罚策略上述的入侵检测模型能够有效检测出恶意节点的攻击行为,但为了保护网络而采取的丢包策略在一定程度上对网络效率和发包成功率带来影响,抑制恶意节点的攻击概率,采取一定的惩罚机制,即在一定时隙t内(0 < t < T),IDS一直对恶意节点采取防御策略,而过完这段时隙,就会将该恶意节点恢复为正常节点,因此可得到攻击者具体的每次博弈收益函数
| $ {U_i} = ({T - t})\sum\limits_{k = 1}^\infty {{{(1 - {\rm{\pi }}_i^*)}^{k - 1}}{\rm{\pi }}_i^*{\delta ^{k - 1}}{U_i}({X})} 。$ | (15) |
式(15) 说明在攻击者的总收益值中将要排除被惩罚时隙的收益值,达到对恶意节点威慑效果,遏制其采取攻击策略的概率。
式(14) 为IDS的收益函数,式(15) 为攻击者的收益函数。同时,由于此模型是基于无限次博弈的过程,对上述2式分别求其平均期望值,可以求出此RMD中,攻击者和IDS的平均收益函数,结果表达式为
| $ {{\bar U}_i} = \frac{{({T - t}){\rm{\pi }}_i^*(1 - \delta )({\delta ^{k - 1}}{U_i}({X}))}}{{(1 - \delta + {\rm{\pi }}_i^*\delta )}}, $ | (16) |
| $ {{\bar U}_i} = \frac{{{\rm{\pi }}_i^*(1 - \delta )({\delta ^{k - 1}}{U_i}({X}))}}{{(1 - \delta + {\rm{\pi }}_i^*\delta )}}。$ | (17) |
式(16) 是攻击者的最终收益函数,式(17) 为IDS的最终收益函数。根据式(16) 可以看出,当延长惩罚时隙t时,攻击者所获得的收益将越来越小,并且将影响攻击者采取攻击策略的概率,同时根据此式的结果,可以求解出在λ不断变化的情况下,攻击者与IDS采取不同的行动策略时所能获得的收益值,并且可以预测出攻击者与IDS在博弈中通过不断学习,改变自身的λ值,并且争取获得最好的收益值,下面将通过实验仿真来验证各项参数。
3 数据仿真及分析为了验证上述公式中各项参数,首先根据式(11) 算出博弈双方的效用矩阵同时用Gambit仿真工具可求出RMD纳什均衡。然后根据式(16)、(17) 求出进一步改进后模型的随机最优反应均衡结果图。最后使用OMNET++进行算法的网络实验仿真,搭建具体的网络场景,布置在500 m×500m的区域面积内,随机放置40个节点,恶意节点8个,同时结合第二步中随机最优反应均衡结果创建不同的数据流,并且对比模型改进前后发包成功率,并且将得到的最终数据用MATLAB绘制曲线图。
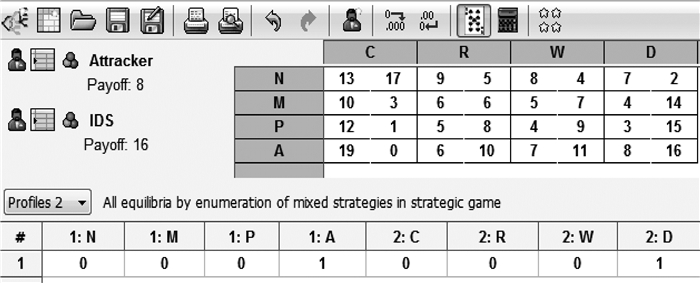
3.1 RMD纳什均衡通过式(11) 以及相关的概念,可以求出博弈双方的效益矩阵,并且根据该矩阵数据,分别求出该RMD模型4×4策略下收益值的纳什均衡,结果如图 1所示。
|
图 1 RMD纳什均衡 |
图 1所示,上半部分中的表格为式(11) 计算所得的效益矩阵,下半部分中的表格为由此效益矩阵分析求出的该RMD模型4×4策略下收益值的纳什均衡,得出此RMD模型在趋于纳什均衡为AD=Sad=(SA, SD),即攻击者采取攻击策略,IDS进行防御的情况下,双方能获得最大的收益。
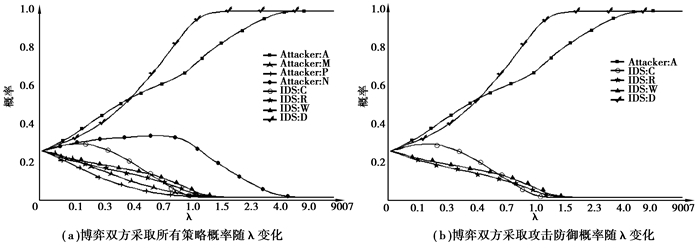
3.2 随机最优反应均衡根据式(16)、(17),利用Gambit进行仿真计算得到RMD随机最优反应均衡结果图,攻击者与IDS的博弈过程中根据λ的变化,不断改变自己的行动策略,最终趋向纳什均衡,其结果如图 2所示。
|
图 2 随机最优反应均衡结果 |
由图 2(a)可以看出刚开始博弈双方由于无法辨别各自的优劣策略,所以都是等概率的选择策略集中各个策略,因此选择每种行动策略的概率都为0.25。从图 2(b)可以看出,通过学习,攻击者发现攻击能带来最高收益,伴随着λ的增大,攻击者更多的采取攻击策略,而与此同时IDS采取防御的策略概率也逐渐增大。当λ增大到0.4时,IDS采取防御策略的概率会超过攻击者,对比图 1中纳什均衡的结果,在当λ取某个特定的值时,随机最优反应均衡结果也会无限趋于纳什均衡,即是在该模型中,攻击者始终采用攻击策略,IDS则采取防御策略。在该模型中,攻击者通过不断学习,将会采取不断的攻击以获得自己最大的效益值;同时IDS也会随着λ的改变,不断学习,进而采取防御策略,最终整个模型将趋于纳什均衡。
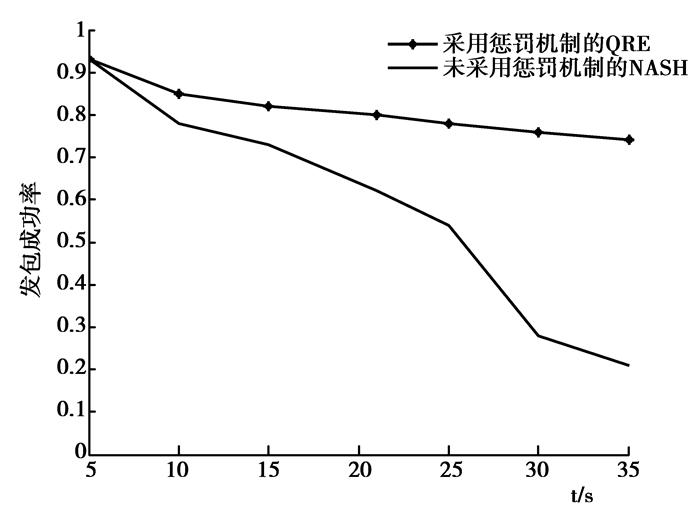
3.3 发包成功率对比研究采用OMNET++搭建网络环境,具体参数为500 m×500 m的区域面积内,随机放置40个节点,恶意节点8个,并且根据模型中攻击者和IDS不同的行动策略创建不同的数据包,并且根据上述随机最优反应均衡结果创建不同的数据流,同时此仿真主要是对模型改进前后发包成功率的影响进行考察,并且将结果数据用MATLAB绘制成曲线,如图 3所示。
|
图 3 数据发包成功率对比 |
由图 3可知,刚开始,改进后的模型与改进前趋于纳什均衡模型发包成功率基本相同,但是随着时间的推移,改进前趋于纳什均衡模型由于没有采取惩罚机制,将对恶意节点持续采取防御策略,降低网络整体发包成功率,而该改进后的模型在采取惩罚措施后,会动态的调节各阶段的均衡,从而提高节点的发包成功率,因此该改进后的模型不仅能检测出恶意节点的攻击行为,而且还能在一定程度上提高网络数据的发包成功率。
4 结论基于博弈理论,构建了一种重复博弈模型,并且结合随机最优反应均衡算法优化此模型,使得其更加适应实际网络情况同时验证改进后的模型最终能够趋于纳什均衡。每次博弈过程中攻击者与IDS会根据历史经验行为不断学习,并且最终采取对自己最有利的行动策略,因此根据此种机制,在实际的物联网应用中能够有效地检测出恶意节点的入侵攻击,对物联网的安全进行防护。同时,本模型能够在检测到恶意节点的攻击行为后,动态调整每阶段博弈的均衡,提高网络数据发包的成功率,有效利用了传感节点的宝贵能源,并显现出其在性能方面的优越性和良好应用前景。
| [1] |
林闯.
物联网关键理论与技术[J]. 计算机学报, 2011, 34(5): 761–762.
LIN Chuang. The key theory and technology in Internet of Things[J]. Chinese Journal of Computers, 2011, 34(5): 761–762. (in Chinese) |
| [2] |
张毅, 唐红.
物联网综述[J]. 数字通信, 2010, 37(4): 24–27.
ZHANG Yi, TANG Hong. Review on Internet of Things[J]. Digital Communication, 2010, 37(4): 24–27. (in Chinese) |
| [3] |
邬贺铨.
物联网的应用与挑战综述[J]. 重庆邮电大学学报:自然科学版, 2010, 22(5): 526–531.
WU Hequan. Review on Internet of Things:application and challenges[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2010, 22(5): 526–531. (in Chinese) |
| [4] |
宁焕生, 徐群玉.
全球物联网发展及中国物联网建设若干思考[J]. 电子学报, 2010, 38(11): 2590–2599.
NING Huansheng, XU Qunyu. Research on global Internet of Things' developments and it's lonstruction in China[J]. Acta Electronica Sinica, 2010, 38(11): 2590–2599. (in Chinese) |
| [5] |
杨庚, 许建, 陈伟, 等.
物联网安全特征与关键技术[J]. 南京邮电大学学报:自然科学版, 2010, 30(4): 20–29.
YANG Geng, XU Jian, CHEN Wei, et al. Security characteristic and technology in the Internet of Things[J]. Journal Of Nanjing University Of Posts and Telecommunications:Natural Science Edition, 2010, 30(4): 20–29. (in Chinese) |
| [6] | Farooqi A H, Khan F A. A survey of intrusion detection systems for wireless sensor networks[J]. International Journal of Ad Hoc and Ubiquitous Computing, 2012, 9(2): 69–83. DOI:10.1504/IJAHUC.2012.045549 |
| [7] | Jadidoleslamy H. A high-level architecture for intrusion detection on heterogeneous wireless sensor networks:hierarchical, scalable and dynamic reconfigurable[J]. Wireless Sensor Network, 2011, 3(7): 241–261. DOI:10.4236/wsn.2011.37026 |
| [8] | Krontiris I, Benenson Z, Giannetsos T, et al. Cooperative intrusion detection in wireless sensor networks[J]. Lecture Notes in Computer Science, 2009, 5432: 263–278. DOI:10.1007/978-3-642-00224-3 |
| [9] | Gacia T P, Diaz V J, Macia F G, et al. Anomaly-based network intrusion detection:Techniques, systems and challenges[J]. Computers & Security, 2009, 28(1-2): 18–28. |
| [10] | Zhou C V, Leckie C, Karunasekera S. A survey of coordinated attacks and collaborative intrusion detection[J]. Computers & Security, 2010, 29(1): 124–140. |
| [11] |
刘勇国, 李学明, 廖晓峰, 等.
基于数据挖掘的入侵检测[J]. 重庆大学学报:自然科学版, 2002, 25(10): 128–131.
LIU Yongguo, LI Xueming, LIAO Xiaofeng, et al. Intrusion detection based on data mining[J]. Journal of Chongqing University:Natural Science Edition, 2002, 25(10): 128–131. (in Chinese) |
| [12] |
杨元凉, 马文平, 刘维博, 等.
有效的多协议攻击自动化检测系统[J]. 重庆大学学报, 2012, 35(2): 71–77.
YANG Yuanliang, MA Wenping, LIU Weibo, et al. An effective automatic detection system for multi-protocol attack[J]. Journal of Chongqing University, 2012, 35(2): 71–77. DOI:10.11835/j.issn.1000-582X.2012.02.012 (in Chinese) |
| [13] | Shen S G, Yue G X, Cao Q Y. A survey of game theory in wireless sensor networks security[J]. Journal of Networks, 2011, 6(3): 521–532. |
| [14] | Akkarajitsakul K, Hossain E, Niyato D, et al. Game theoretic approaches for multiple access in wireless networks:A survey[J]. Communications Surveys & Tutorials, 2011, 13(3): 372–395. |
| [15] | Reddy Y B.A game theory approach to detect malicious nodes in wireless sensor networks[C]//Proceedings of 2009 the 3rd International Conference on Sensor Technologies and Applications, Washington DC:IEEE Computer Society, 2009:462-468. |
| [16] | Agah A, Das S K, Basu K, et al.Intrusion detection in sensor networks:A non-cooperative game approach[C]//Proceedings of Third IEEE International Symposium on Network Computing and Applications, August 30-September 1, 2004, Cambridge, MA, USA.Piscataway:IEEE Press, 2004:343-346. |
| [17] | Mckelvey R D, Palfrey T R. Quantal response equilibrium for normal form games[J]. Games and Economic Behavior, 1995, 10(1): 6–38. DOI:10.1006/game.1995.1023 |
| [18] |
王博, 黄传河, 杨文忠, 等.
Ad Hoc网络中基于惩罚机制的激励合作转发模型[J]. 计算机研究与发展, 2011, 48(3): 398–406.
WANG Bo, HUANG Chuanhe, YANG Wenzhong, et al. An incentive-cooperative forwarding model based on punishment mechanism in wireless ad hoc networks[J]. Journal of Computer Research and Development, 2011, 48(3): 398–406. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

