多相电机系统相对于三相系统而言具有谐波最低次数和脉动频率高、力矩脉动小、转子谐波损耗小、力矩密度大和电机噪声小等优点[1-6]。要推出技术性能优良的机车牵引、机器人、纺织、造纸等工业驱动系统以及综合电力舰船系统,需要解决同一直流母线电源下的多台多电机驱动系统中各电机能同时独立运行的问题。根据电机理论,如果采用多于五相的多相电机取代传统的三相电机,以多台电机串联的方式则可以实现单台逆变器驱动的多台电机的独立运行[7-10]。文中研究了一种单逆变器供电下对称六相PMSM串联三相PMSM的新型多电机系统[11-12]。在理想正弦波反电动势(EMF)下2台电机的转速和负载互不影响,可以实现2台电机的独立运行[13-14]。但由于实际电机通常为非正弦EMF,高次谐波会影响2台电机的解耦运行,现有文献主要以多相感应电机的串联为例,从控制原理上证明了理想情况下该新型驱动系统的可行性,对于2台永磁同步电机的串联系统高次谐波的耦合与解耦控制方面还未见文献报道。文中建立了对称六相PMSM含有2次谐波时串联系统的数学模型,分析了反电动势2次谐波引起的串联系统电磁转矩脉动表达式,提出了补偿反电动势谐波效应的控制策略,通过变载和变速仿真证明了所提控制策略的可行性。
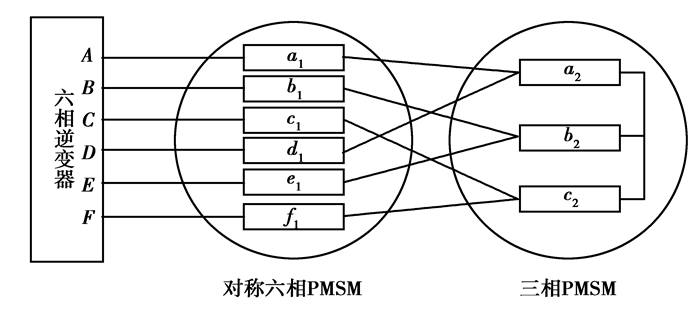
1 对称六相PMSM反电动势含有2次谐波时的耦合运行 1.1 串联系统数学模型的建立对称六相PMSM串联三相PMSM如图 1所示。
|
图 1 对称六相PMSM串联三相PMSM |
当定子绕组在空间上完全对称分布时,磁动势中理论上不会产生偶次谐波,但若采用短距集中绕组导致相绕组空间上分布不对称时,定子绕组函数也呈不对称状态,则绕组产生的磁动势中奇次和偶次谐波都将存在,经分析可知其中对称六相PMSM反电动势中的2, 4, 8, 10, …,6i±2(i=0, 1, 2, 3, …)次谐波,会在对称六相PMSM中产生受三相PMSM干扰的转矩和转速脉动,影响了串联系统的解耦控制,而六相PMSM反电动势中的各奇次谐波则不受三相PMSM的干扰,进而不影响串联系统的解耦控制[14]。考虑到2次谐波的含量明显高于4、8、10…等高次谐波,为简化分析,只研究对称六相PMSM反电动势中含有2次谐波的情况。做如下假设[15]:1) 电机磁路线性,铁芯的涡流、磁滞损耗忽略不计;2) 定子表面光滑,忽略齿槽效应;3) 忽略由气隙不均引起的电感变化;4) 电机为面装式PMSM,交直轴电抗相等。
设对称六相PMSM定子绕组中由永磁励磁磁场产生的磁链为
| $ {\mathit{\boldsymbol{\psi }}_{{\rm{sr1}}}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{\psi }}_{{\rm{ar1}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{br1}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{cr1}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{dr1}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{er1}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{fr1}}}} \end{array} \right] = {N_{{\rm{s1}}{\varphi _{{\rm{fm}}}}_{\rm{1}}}}\left[ \begin{array}{l} \;\;\;\;{\rm{cos(}}{\theta _{{\rm{r1}}}}{\rm{)}}\\ \;{\rm{cos(}}{\theta _{{\rm{r1}}}}{\rm{ - }}{\theta _1}{\rm{)}}\\ {\rm{cos(}}{\theta _{{\rm{r1}}}}{\rm{ - 2}}{\theta _1}{\rm{)}}\\ {\rm{cos(}}{\theta _{{\rm{r1}}}}{\rm{ - 3}}{\theta _1}{\rm{)}}\\ {\rm{cos(}}{\theta _{{\rm{r1}}}}{\rm{ - 4}}{\theta _1}{\rm{)}}\\ {\rm{cos(}}{\theta _{{\rm{r1}}}}{\rm{ - 5}}{\theta _1}{\rm{)}} \end{array} \right] + {N_{{\rm{s1 - 2}}{\varphi _{{\rm{fm1}}}}_{{\rm{ - 2}}}}}\left[ \begin{array}{l} \;\;\;\;{\rm{cos(2}}\theta {\rm{r1)}}\\ \;{\rm{cos(2}}{\theta _{{\rm{r1}}}}{\rm{ - 2}}{\theta _1}{\rm{)}}\\ {\rm{cos(2}}{\theta _{{\rm{r1}}}}{\rm{ - 4}}{\theta _1}{\rm{)}}\\ {\rm{cos(2}}{\theta _{{\rm{r1}}}}{\rm{ - 6}}{\theta _1}{\rm{)}}\\ {\rm{cos(2}}{\theta _{{\rm{r1}}}}{\rm{ - 8}}{\theta _1}{\rm{)}}\\ {\rm{cos(2}}{\theta _{{\rm{r1}}}}{\rm{ - 10}}{\theta _1}{\rm{)}} \end{array} \right], $ | (1) |
式中:θ1=60°;
三相PMSM定子绕组中由永磁励磁磁场产生的磁链为
| $ {\mathit{\boldsymbol{\psi }}_{{\rm{sr2}}}} = \left[\begin{array}{l} {\mathit{\boldsymbol{\psi }}_{{\rm{ar2}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{br2}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{cr2}}}} \end{array} \right] = {N_{{\rm{s2}}{\varphi _{{\rm{fm}}}}_2}}\left[\begin{array}{l} \;\;\;\;{\rm{cos(}}{\theta _{{\rm{r2}}}}{\rm{)}}\\ \;{\rm{cos(}}{\theta _{{\rm{r2}}}}{\rm{-}}{\theta _2}{\rm{)}}\\ {\rm{cos(}}{\theta _{{\rm{r2}}}}{\rm{-2}}{\theta _2}{\rm{)}} \end{array} \right], $ | (2) |
式中:θ2=120°;
设六相逆变器输出电流为Is=[iA iB iC iD iE iF]T,对称六相PMSM定子绕组的总磁链为
| $ {\mathit{\boldsymbol{\psi }}_{{\rm{s1}}}} = {\mathit{\boldsymbol{L}}_{{\rm{s1}}}}{\mathit{\boldsymbol{I}}_{\rm{s}}} + {\mathit{\boldsymbol{\psi }}_{{\rm{sr1}}}}。$ | (3) |
式中
| $ \begin{array}{l} {\mathit{\boldsymbol{L}}_{{\rm{s1}}}} = {L_{{\rm{s}}\sigma {\rm{1}}}}{\mathit{\boldsymbol{E}}_1} + {L_{{\rm{sm1}}}}\left( \begin{array}{l} \;\;1\;\;\;\;\;\;\;\;\cos {\theta _1}\;\;\;\;\;\cos 2{\theta _1}\;\;\cos 3{\theta _1}\;\;\cos 4{\theta _1}\;\;\cos 5{\theta _1}\\ \cos {\theta _1}\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\;\cos \;{\theta _1}\;\;\;\;\cos \;2{\theta _1}\;\;\cos 3{\theta _1}\;\;\cos 4{\theta _1}\\ \cos 2{\theta _1}\;\;\cos {\theta _1}\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\cos {\theta _1}\;\;\;\cos 2{\theta _1}\;\;\cos 3{\theta _1}\\ \cos 3{\theta _1}\;\;\;\cos 2{\theta _1}\;\;\cos {\theta _1}\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\cos {\theta _1}\;\;\;\;\cos 2{\theta _1}\\ \cos 4{\theta _1}\;\;\;\cos 3{\theta _1}\;\;\;\cos 2{\theta _1}\;\;\;\cos {\theta _1}\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\cos {\theta _1}\\ \cos 5{\theta _1}\;\;\;\;\cos 4{\theta _1}\;\;\cos 3{\theta _1}\;\;\cos 2{\theta _1}\;\;\cos {\theta _1}\;\;\;\;\;1\; \end{array} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{L_{{\rm{sm1}}}} - 2\left( \begin{array}{l} \;\;1\;\;\;\;\;\;\;\;\cos 2{\theta _1}\;\;\;\;\cos 4{\theta _1}\;\;\cos 6{\theta _1}\;\;\cos 8{\theta _1}\;\;\cos 10{\theta _1}\\ \cos 2{\theta _1}\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\cos 2{\theta _1}\;\;\;\cos 4{\theta _1}\;\;\cos 6{\theta _1}\;\;\cos 8{\theta _1}\\ \cos 4{\theta _1}\;\;\cos 2{\theta _1}\;\;\;\;\;\;\;\;\;1\;\;\;\;\;\;\cos 2{\theta _1}\;\;\cos 4{\theta _1}\;\;\cos 6{\theta _1}\\ \cos 6{\theta _1}\;\;\;\cos 4{\theta _1}\;\;\cos 2{\theta _1}\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\cos 2{\theta _1}\;\;\cos 4{\theta _1}\\ \cos 8{\theta _1}\;\;\;\cos 6{\theta _1}\;\;\cos 4{\theta _1}\;\;\cos 2{\theta _1}\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\cos 2{\theta _1}\\ \cos 10{\theta _1}\;\;\cos 8{\theta _1}\;\;\cos 6{\theta _1}\;\;\cos 4{\theta _1}\;\;\;\;\cos 2{\theta _1}\;\;\;\;\;1\; \end{array} \right), \end{array} $ |
式中,Lsσ1为定子漏感,Lsm1为主磁通电感,Lsm1-2为2次谐波电感。
对称六相PMSM定子绕组的电压方程为
| $ {\mathit{\boldsymbol{U}}_{{\rm{s1}}}} = {\mathit{\boldsymbol{R}}_{{\rm{s1}}}}{\mathit{\boldsymbol{I}}_{\rm{s}}} + \frac{{\rm{d}}}{{{\rm{d}}\mathit{t}}}{\mathit{\boldsymbol{\psi }}_{{\rm{s1}}}}{\rm{, }} $ | (4) |
式中六阶矩阵Rs1=diag(rs1)。
因逆变器输出的是六相物理量,需对三相PMSM进行拓展为
| $ {{\mathit{\boldsymbol{\psi '}}}_{{\rm{sr2}}}} = \left[\begin{array}{l} {\mathit{\boldsymbol{\psi }}_{{\rm{sr2}}}}\\ {\mathit{\boldsymbol{\psi }}_{{\rm{sr2}}}} \end{array} \right], $ | (5) |
| $ {{\mathit{\boldsymbol{L'}}}_{{\rm{s2}}}} = \left[\begin{array}{l} {L_{{\rm{s2}}}}\;\;{L_{{\rm{s2}}}}\\ {L_{{\rm{s2}}}}\;\;{L_{{\rm{s2}}}} \end{array} \right], $ | (6) |
式中
| $ {\mathit{\boldsymbol{L}}_{{\rm{s2}}}} = \left( {{L_{{\rm{s}}\sigma {\rm{2}}}}{\mathit{\boldsymbol{E}}_2} + {L_{{\rm{sm2}}}}\left( \begin{array}{l} \;\;\;1\;\;\;\;\;\;\cos \;{\theta _2}\;\;\cos \;2{\theta _2}\\ \cos \;{\theta _2}\;\;\;\;\;1\;\;\;\;\;\;\;\cos \;{\theta _2}\\ \cos \;2{\theta _2}\;\cos \;{\theta _2}\;\;\;\;\;1 \end{array} \right)} \right); $ |
Lsσ2为定子漏感,Lsm2为主磁通电感。
扩展后三相PMSM定子绕组的总磁链为
| $ {{\mathit{\boldsymbol{\psi '}}}_{{\rm{s2}}}} = {{\mathit{\boldsymbol{L'}}}_{{\rm{s2}}}}{\mathit{\boldsymbol{I}}_{\rm{s}}} + {{\mathit{\boldsymbol{\psi '}}}_{{\rm{sr2}}}}。$ | (7) |
三相PMSM定子绕组的电压方程为
| $ {\mathit{\boldsymbol{U}}_{{\rm{s2}}}} = {{\mathit{\boldsymbol{R'}}}_{{\rm{s2}}}}{\mathit{\boldsymbol{I}}_{\rm{s}}} + \frac{{\rm{d}}}{{{\rm{d}}\mathit{t}}}{\mathit{\boldsymbol{\psi }}_{{\rm{s2}}}}{\rm{, }} $ | (8) |
式中, 扩展矩阵
2台电机定子绕组的电压方程相加得到逆变器输出电压的方程为
| $ {\mathit{\boldsymbol{U}}_{\rm{s}}} = {\mathit{\boldsymbol{U}}_{{\rm{s1}}}} + {\mathit{\boldsymbol{U}}_{{\rm{s2}}}} = ({\mathit{\boldsymbol{R}}_{{\rm{s1}}}} + {{\mathit{\boldsymbol{R'}}}_{{\rm{s2}}}}){\mathit{\boldsymbol{I}}_{\rm{s}}} + \frac{{\rm{d}}}{{{\rm{d}}\mathit{t}}}{\mathit{\boldsymbol{\psi }}_{{\rm{s1}}}} + \frac{{\rm{d}}}{{{\rm{d}}\mathit{t}}}{{\mathit{\boldsymbol{\psi '}}}_{{\rm{s2}}}}。$ | (9) |
利用旋转坐标变换矩阵,可以得到d-q两相旋转坐标系下的串联系统数学模型。令
| $ \left\{ \begin{array}{l} {u_{{d}{\rm{1}}}} = {r_1}{i_{d1}} + {L_1}\frac{{\rm{d}}}{{{\rm{d}}{t}}} - {\omega _{{\rm{r1}}}}{L_1}{i_{q1}}, \\ {u_{q1}} = {r_1}{i_{q1}} + {L_1}\frac{{\rm{d}}}{{{\rm{d}}{t}}}{i_{q1}} - {\omega _{{\rm{ri}}}}{L_1}{i_{d1}} + {\omega _{{\rm{r1}}}}{\psi _{{\rm{f1}}}}。\end{array} \right. $ | (10) |
设定ψf2=
| $ \left\{ \begin{array}{l} {u_{{d2}}} = {r_2}{i_{d2}} + {{L'}_2}\frac{{\rm{d}}}{{{\rm{d}}{t}}}{i_{d2}} - {\omega _{{\rm{r2}}}}{{L'}_2}{i_{q2 + }}{\omega _{{\rm{r1}}}}{\psi _{{\rm{f1 - 2}}}}{\rm{sin}}({\theta _{{\rm{r2}}}} - 2{\theta _{{\rm{r1}}}}), \\ {u_{q2}} = {r_2}{i_{q2}} + {{L'}_2}\frac{{\rm{d}}}{{{\rm{d}}{t}}}{i_{q2}} - {\omega _{{\rm{r2}}}}{{L'}_2}{i_{d2}} + {\omega _{{\rm{r2}}}}{\psi _{{\rm{f2}}}} + {\omega _{{\rm{r1}}}}{\psi _{{\rm{f1 - 2}}}}{\rm{cos}}({\theta _{{\rm{r2}}}} - 2{\theta _{{\rm{r1}}}})。\end{array} \right. $ | (11) |
两相旋转坐标系下对称六相PMSM的转矩方程为
| $ {{T}_{{\rm{e1}}}} = {p_1} \cdot {\psi _{{\rm{f1}}}} \cdot {i_{q1}} - {p_1}{\psi _{{\rm{f1 - 2}}}}{i_{d2}}{\rm{sin(}}{\theta _{{\rm{r2}}}} - 2{\theta _{{\rm{r1}}}}{\rm{) - }}{p_1} \cdot {\psi _{{\rm{f1 - }}}}_2{i_{q2}}{\rm{cos(}}{\theta _{{\rm{r2}}}} - 2{\theta _{{\rm{r1}}}}{\rm{)}}。$ | (12) |
两相旋转坐标系下三相PMSM的转矩方程为
| $ {T_{e2}} = {p_2} \cdot {\psi _{{\rm{f2}}}}{i_{q2}}。$ | (13) |
对称六相PMSM转矩脉动Ts1在两相旋转坐标系下的表达式为
| $ {{T}_{{\rm{s1}}}} = - {\psi _{{\rm{f1 - }}}}_2{p_1}{i_{d2}}{\rm{sin(2}}{\theta _{{\rm{r1}}}} - {\theta _{{\rm{r2}}}}{\rm{) - }}{\psi _{{\rm{f1 - 2}}}}{p_1}{i_{q2}}{\rm{cos(2}}{\theta _{{\rm{r1}}}} - {\theta _{{\rm{r2}}}}{\rm{)}}。$ | (14) |
设Ωr1为对称六相PMSM的机械角速度、J1为转动惯量、F1为摩擦系数、Tl1为负载转矩,则对称六相PMSM的机械运动方程为
| $ {\mathit{J}_1}\frac{{{\rm{d}}{\mathit{\Omega }_{{\rm{r1}}}}}}{{{\rm{d}}\mathit{t}}} = {T_{{\rm{e1}}}} - {F_1}{\mathit{\Omega }_{{\rm{r1}}}} - {T_{{\rm{l1}}}} $ | (15) |
设Ωr2为三相PMSM的机械角速度、J2为转动惯量、F2为摩擦系数、Tl2为负载转矩,则三相PMSM的机械运动方程为
| $ {\mathit{J}_2}\frac{{{\rm{d}}{\mathit{\Omega }_{{\rm{r2}}}}}}{{{\rm{d}}\mathit{t}}} = {T_{{\rm{e2}}}} - {F_2}{\mathit{\Omega }_{{\rm{r2}}}} - {T_{{\rm{l2}}}}。$ | (16) |
由式(14) 可以看出,转矩脉动Ts1的频率和2台电机的速度有关、幅值受三相PMSM电流的影响,对对称六相PMSM的运行产生一定影响。根据式(12)、(15) 可知,对称六相PMSM转矩的脉动会造成电机转速的波动,波动频率和幅值都受到了三相PMSM的影响。根据式(13) 可见,三相PMSM的运行不受对称六相PMSM的任何影响。
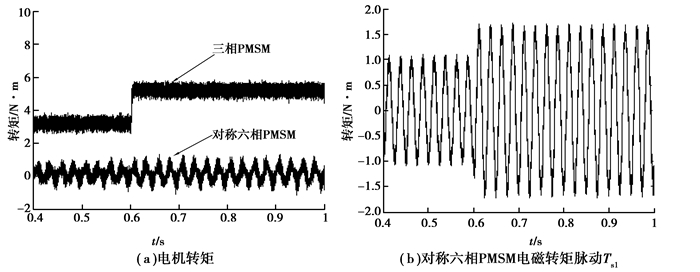
1.2 对称六相PMSM反电动势含有2次谐波的仿真1) 三相PMSM变载仿真:对称六相PMSM空载转速为300 r/min,三相PMSM负载为3 N·m、转速为200 r/min,在t=0.6 s三相PMSM负载变为5 N·m,串联系统的运行状态如图 2所示。
|
图 2 三相PMSM变载时串联系统运行状态 |
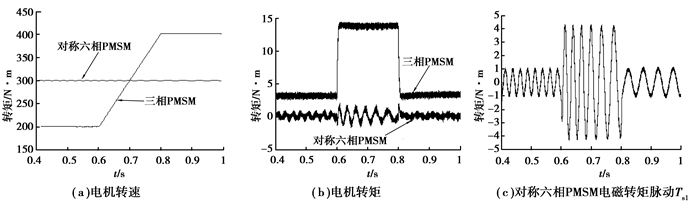
2) 三相PMSM变速仿真:对称六相PMSM空载转速为300 r/min,三相PMSM负载为3 N·m、转速为200 r/min,在t=0.6 s三相PMSM开始加速到400 r/min,串联系统的运行状态如图 3所示。
|
图 3 三相PMSM变速时串联系统运行状态 |
由上述仿真可知:1) 控制方式不变的情况下,对称六相PMSM反电动势含有2次谐波时,产生的电磁转矩Ts1会对对称六相PMSM的电磁转矩产生扰动,使其转速产生波动;2) 三相PMSM变速时会导致对称六相PMSM中Ts1及转速的波动频率都发生变化;3) 三相PMSM转矩的变化会影响Ts1和对称六相PMSM转速波动的幅值。因此,该串联系统的2台电机无法实现独立运行。
2 消除对称六相PMSM反电动势中谐波影响的控制策略为了消除对称六相PMSM反电动势含有2次谐波对串联系统解耦控制的影响,在此提出了一种转矩脉动补偿的解耦控制策略。
由式(14) 可知,对称六相PMSM转矩脉动产生的直接原因是三相PMSM的转矩和励磁电流分量和对称六相PMSM的谐波磁链之间的相互耦合作用,因此通过测量对称六相PMSM转子角速度、三相PMSM的电流分量提前设定反电动势中谐波含量得到Ts1,按照式(17) 来修正电磁转矩,消除三相PMSM对对称六相PMSM转矩的干扰,实现串联电机的解耦控制。
| $ T_{1修正}^* = T_1^* - {T_{{\rm{s1}}}}。$ | (17) |
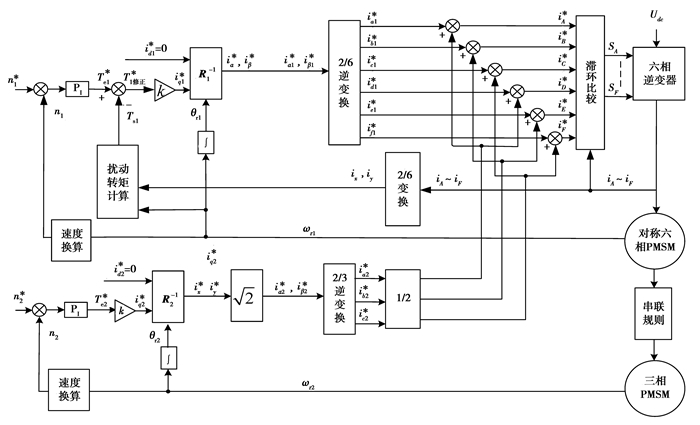
基于转矩脉动补偿控制策略的串联系统原理图如图 4所示。
|
图 4 基于辅电机转矩补偿的串联系统控制原理图 |
三相PMSM变速仿真:对称六相PMSM负载为4 N·m、转速为400 r/min,三相PMSM空载转速为200 r/min,在t=0.8 s三相PMSM开始加速到300 r/min,系统的运行状态如图 5所示。

|
图 5 三相PMSM变速状态下系统运行状态 |
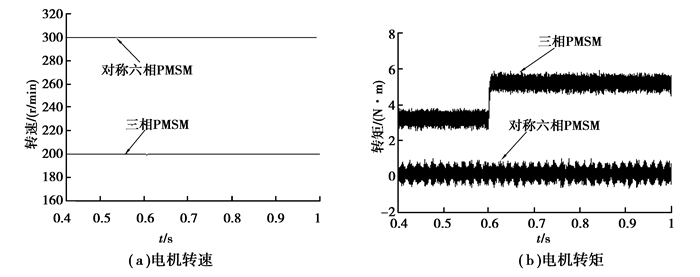
三相PMSM变载仿真:对称六相PMSM空载转速为300 r/min,三相PMSM负载为3 N·m、转速为200 r/min,在t=0.6 s三相PMSM负载变为5 N·m,系统的运行状态如图 6所示。
|
图 6 三相PMSM变载状态下系统运行状态 |
从上述变速和变载仿真结果可知:通过反电动势谐波效应的补偿控制,即对电磁转矩进行修正,可以消除对称六相PMSM的反电动势2次谐波在对称六相PMSM中引起的转矩脉动和转速波动,使2台电机的转速和转矩不受串联电机的影响,实现了串联系统解耦控制。
3 结论研究了对称六相PMSM反电动势的谐波对串联系统解耦控制的影响情况,建立了对称六相PMSM反电动势含有2次谐波时的串联系统数学模型,对谐波引起的对称六相PMSM电磁转矩的脉动进行了推导,其幅值受三相PMSM负载转矩的影响、频率与2台电机的同步转速有关。为了实现串联系统的解耦控制,提出了补偿反电动势谐波效应的控制策略,通过变载和变速仿真证明了所提控制策略可以实现该串联系统的解耦控制。
| [1] | Nelson R H, Krause P C. Induction machine analysis for arbitrary displacement between multiple winding sets[J]. IEEE Transactions Power Apparatus and System, 1994, 93(3): 841–848. |
| [2] | Abbas M A, Christen R, Jahns T M. Six-phase voltage source inverter driven induction motor[J]. IEEE Transactions on Industry Applications, 1984, 20(5): 1251–1259. |
| [3] | Levi E. Multiphase electric machines for variable-speed applications[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 1893–1909. DOI:10.1109/TIE.2008.918488 |
| [4] | Singh G K. Multi-phase induction machine drive research-A survey[J]. Electric Power System Research, 2002, 61(2): 139–147. DOI:10.1016/S0378-7796(02)00007-X |
| [5] |
杨金波, 杨贵杰, 李铁才.
双三相永磁同步电机的建模与矢量控制[J]. 电机与控制学报, 2010, 14(6): 1–7.
YANG Jinbo, YANG Guijie, LI Tiecai. Modeling and vector control for dual three-phase PMSM[J]. Electric Machines and Control, 2010, 14(6): 1–7. (in Chinese) |
| [6] |
欧阳红林, 成兰仙.
多相永磁同步电机模糊神经网络控制调速系统[J]. 电机与控制学报, 2007, 11(2): 111–115.
OUYANG Honglin, CHENG Lanxian. Multiple phase permanent magnet synchronous motor speed control system based on fuzzy neural network control[J]. Electric Machines and Control, 2007, 11(2): 111–115. (in Chinese) |
| [7] | Levi E, Jones M, Vukosavic S N, et al. A novel concept of a multiphase, multi-motor vector controlled drive system supplied from a single voltage source inverter[J]. IEEE Transactions on Power Electronics, 2004, 19(2): 320–335. DOI:10.1109/TPEL.2003.823241 |
| [8] | Levi E, Jones M, Toliyat H A. Operating principles of a novel multiphase multi-motor vector-controlled drive[J]. IEEE Transactions on Energy Conversion, 2004, 19(3): 508–517. DOI:10.1109/TEC.2004.832055 |
| [9] | Levi E, Vukosavic S N, Jones M. Vector control schemes for series-connected six-phase two-motor drive systems[J]. IEE Proceedings-Electric Power Applications, 2005, 152(2): 226–238. DOI:10.1049/ip-epa:20055018 |
| [10] | Levi E. Even-phase multi-motor vector controlled driver with single inverter supply and series connection of stator windings[J]. IEE Proceedings Electric Power Applications, 2003, 150(5): 580–591. DOI:10.1049/ip-epa:20030424 |
| [11] | Levi E, Jones M, Vukosavic S N. A series-connected two-motor six-phase drive with induction and permanent magnet machines[J]. IEEE Transactions on Energy Conversion, 2006, 21(1): 121–129. DOI:10.1109/TEC.2005.853737 |
| [12] | Correa M B R, Silva C R. Independent voltage control for series connected six-phase and three-phase induction machines[J]. IEEE Transactions on Industry Application, 2009, 45(4): 1287–1293. |
| [13] | Semail e, Levi E, Bouscayrol A, et al.Multi-machine modeling of two series connected 5-phase synchronous machines:effect of harmonics on control[C]//Proceedings of 2005 European Conference on Power Electronics and Applications, September 11-14, 2005, Dresden, Germany, Piscataway:IEEE Press, 2005:1-10. |
| [14] | Levi E, Jones M, Vukosavic S N, et al.Stator winding design for multi-phase two-motor drives with single VSI supply[C]//Proceedings International Conference Electrical Mchines, Chania, Greece, 2006, CD-ROM, Paper OMM2-1. |
| [15] |
周胜灵, 刘峰.
永磁同步电机直接转矩控制系统的改进及仿真[J]. 重庆大学学报, 2013, 36(11): 87–92.
ZHOU Shengling, LIU Feng. Improvement and simulation on direct torque control system of permanent magnet synchronous motor[J]. Journal of Chongqing University, 2013, 36(11): 87–92. DOI:10.11835/j.issn.1000-582X.2013.11.014 (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

