电力设备状态检修模式的推广应用,对电缆的在线监测及带电测试提出了更高的要求。目前,国内对电缆终端的局部放电[1-8]带电测试主要有甚高频法及超声波法。甚高频法由于很难将外界干扰信号与内部局部放电信号区分开来,现在正处于实验室研究阶段[9-18],现场应用较少,而超声波法因为受外界干扰影响小,近年来在国内开始了广泛的应用。不过从目前的应用情况来看,超声波法存在一个不足,即无法通过测量结果判断出放电点的真实放电水平及放电点的深度,从而无法对放电性质及放电水平作进一步的分析判断。
迄今,安徽电网电力电缆主要应用于10 kV和35 kV电压等级中,终端类型以干式终端为主。文中结合安徽电网实际,以干式电缆终端为例,结合超声波传播理论,对放电点深度和放电点真实放电水平的方法进行理论分析和实验室模拟实验,得到可供现场使用的分析判断方法。
1 局部放电超声波信号的产生与传播电缆终端在局部放电时会伴随着产生许多物理、化学现象,例如:放电空间内有电荷变化,出现脉动电荷;有电磁波辐射;有粒子撞击而发射超声波等。
在放电源点超声波产生后,以球状向周围传播,由于超声波的波长很短,传播过程中衍射能力很差,表现出一定的定向传播特性;超声波传播过程中在不同介质分界面发生折射、反射;此外,超声波携带能量,在其传播过程中必然受到损失,使声强逐渐降低,发生衰减。
电缆终端内部因局部放电产生超声波时,超声波向周围传播,在传播时随着传播距离的增加衰减增大,超声波传播过程中的衰减公式为
| $ {A_x} = {A_{{{\rm{e}}^{ - {a_f}x}}}}, $ | (1) |
式中:Ax为距离探头x处的声振幅,A为声源振幅,af为衰减系数,f为超声频率,x为探头与声源之间的距离。
| $ {{a}_f} = af + b{f^2} + c{f^4}, $ | (2) |
式中:a为介质弹性摩擦吸收系数,b为介质粘滞性与热传导的吸收系数,c为介质内散射体的瑞利散射吸收系数。
2 模拟计算 2.1 坐标系及相关参量说明为便于分析计算,采用圆柱坐标系(ρ,
|
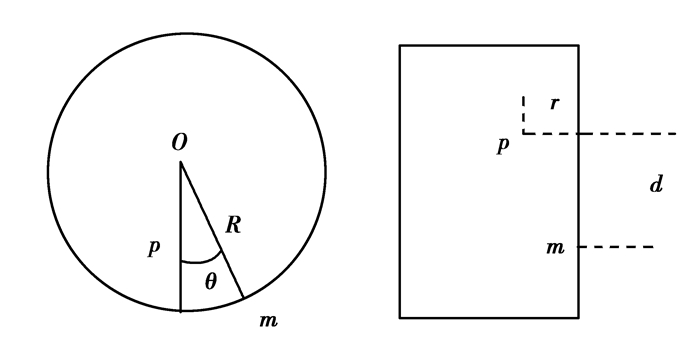
图 1 参量示意图 |
假设R表示不计伞裙尺寸时终端横截面半径(切向),R表示放电点深度,d表示放电点对应终端表面与测量点之间的轴向距离,θ表示放电点与测量点之间切向圆心角。则
| $ \left. \begin{array}{l} {R = }{\rho _2}\\ r = {\rho _2} - {\rho _1}\\ \theta = {\varphi _2}\\ d = \left| {{Z_2}} \right| \end{array} \right\}。$ | (3) |
对于某终端表面的点,不考虑伞裙时其ρ坐标等于电缆终端半径时,终端表面点坐标可简略表示为(
以Up表示放电点局部放电信号量,Um表示测点局部放电信号量,Up、Um单位为mV。
2.2 终端表面超声波分布规律按应用场合不同,电缆终端可分为GIS终端、变压器终端、户外终端等类型,户外终端又可分为充油式终端、油纸绝缘终端及干式终端等类型,终端类型不同,其结构差异较大。结合安徽电网实际情况,以现场经验获得的衰减系数0.3,直径60 mm的干式电缆终端为例,假设在其内部r深处有个局部放电超声波源,源点的超声波强度设为100 mV,通过数学软件模拟计算其表面信号分布规律如下。
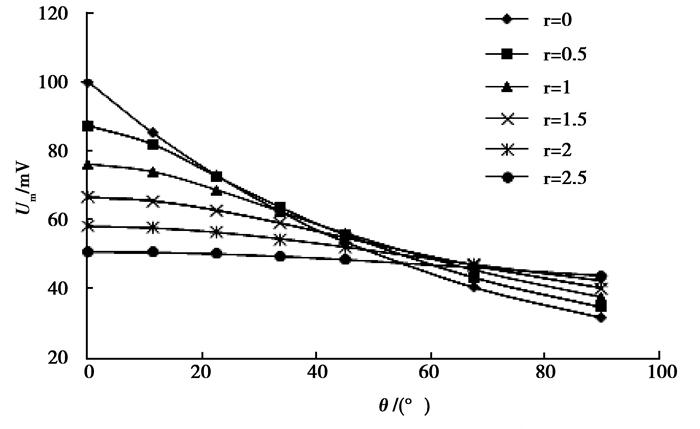
2.2.1 沿切向的分布规律图 2为轴向距离为0时测点信号量与切向夹角的关系图。从上图可以看出信号量与切向夹角的关系,信号量随夹角增大而减小,在45°内,降低较快;放电点深度对信号量随夹角的变化率影响较大,放电点深度越小,变化率越大,反之变化率越小。
|
图 2 切向分布规律 |
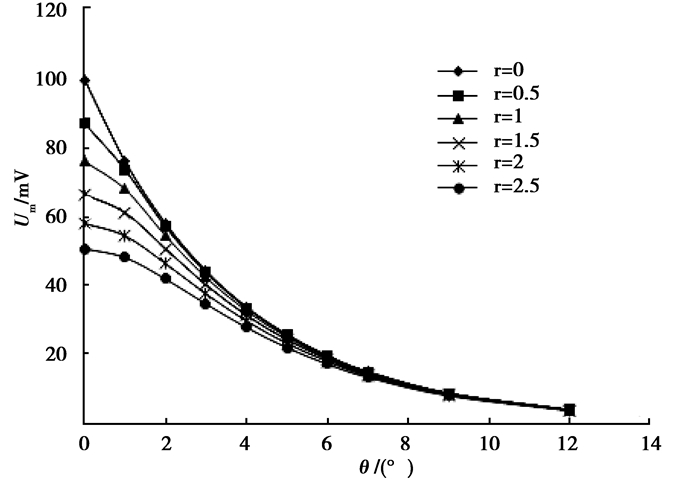
图 3为切向夹角为0时测点信号量与轴向距离的关系图。从图中可以看出信号量与轴向的关系,信号量随轴向距离增大而减小;放电点深度对信号量随轴向距离的变化率影响较大,放电点深度越小,变化率越大,反之变化率越小。
|
图 3 轴向分布规律 |
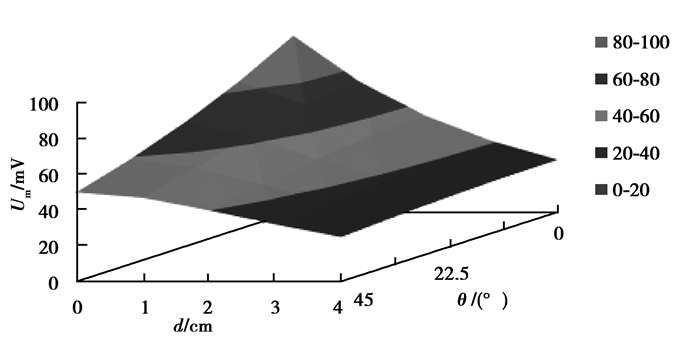
在放电点表面投影(0°, 0 cm)及点(45°,4 cm)组成的表面区域内,超声波信号量分布规律如图 4所示,从图中可以看出,在(45°,4 cm)点的超声波信号量最小。
|
图 4 分布曲面图 |
通过理论分析模拟计算可以看出,对于某个电缆终端或接头,当其结构已知且一定时,信号量值沿其表面的分布规律与放电点的深度之间存在函数关系,根据各测点的测量值通过数学方法分析计算放电源点的深度及信号量值是可行的。
由超声波衰减公式可得到以下的放电源点信号量与测点信号量关系方程为
| $ {C_i} = {\rm{ln}}{{U}_{mi}} = \ln {U_p} - {a_f}\sqrt {d_i^2 + {r^2} + 2{R}{\rm{(}}{R - r}{\rm{)(1 - cos}}{\theta _i}{\rm{), }}} $ | (4) |
式中:信号量值U0为计算时以d为0、θ为0的测点;Ui为第i个测点的测得信号量值;di为第i个测点与之间的轴向距离;θi为第i个测点与之间的切向夹角;R为该电缆终端的半径。
终端表面最大点信号自然对数值C0为
| $ {C_0} = {\rm{ln}}{{U}_{m0}} = \ln {{U}_p} - {a_f}r。$ | (5) |
基于最小二乘法的近似迭代求解方法如下:
1) 将电缆终端半径等分为n个等分,得到n+1个假定深度值,分布为0, 1,…,n。
2) 设第j个假定深度值为rj,aj、Cij分别为对应的第j个深度值的超声衰减系数和第i个测点信号量计算值;Ci、di、θi分别为第i个测点的测得信号量自然对数值、第i个测点与A1之间的轴向距离、切向夹角。
令
| $ Q = \sum\limits_i {{{({{C}_{ij}} - {C_i})}^2}, } $ |
对每个假定深度,按下式分别计算出其aj、Q值为
| $ {a_j} = \frac{{\sum\limits_i {({{C}_0} - {C_i})} }}{{\sum\limits_i {[\sqrt {r_j^2 + d_i^2 + 2R({r-}{{r}_j})(1-{{\rm{cos}}}{\theta _i})}-{r_j}]} }}, $ | (6) |
| $ {Q_j} = \sum\limits_i {{{({{C}_{ij}} - {C_i})}^2} - \sum\limits_i {{{\{ {{C}_0} - {C_i} - {a_j}[\sqrt {r_j^2 + d_i^2 + 2R({R-}{{r}_j})(1-{{\rm{cos}}}{\theta _i})}-{r_j}]\} }^2}} } 。$ | (7) |
3) 比较各深度Q值的大小,取Q值最小的假定深度(第k个)作为基准深度。
4)rk等于0时取k至k+1区间,等于R时,rk取k-1至k区间,其余情况下取k-1至k+1区间,将所取区间分为m等分,并从第2条开始重新计算;当所取区间长度小于所需的精度时,停止计算,则所得的rk值及由此计算出的ak、Up即分别为所求的放电点深度、超声波衰减系数及源点超声波信号量。
3 实验室模拟试验为了验证理论分析的正确性,在实验室针对电缆终端的超声波信号表面分布规律进行了模拟实验。实验采用厚1 cm,半径4 cm的环氧套管电缆终端。实验时将高压尖端引到终端套管外、内表面,让高压尖端对其放电,通过常规局部放电仪监测尖端对终端套管的放电量,并利用超声波局放仪测量终端套管全方位的超声信号。通过模拟试验得到了放电源深度分别为0 cm、1 cm时,不同切向圆心角或轴向表面距离时的测点测量结果,如表 1所示。
| 表 1 实验室模拟试验结果 |
测试结果表明:测得的信号量随轴向距离或夹角的增大而减小,放电点深度对信号量随放电点与测量点间的轴向距离与夹角的变化率有影响,放电点深度较小时,变化率较大,反之,变化率较小。变化规律与理论分析结果一致。
为验证前文迭代方法的正确性,选取其中轴向距离0 cm、3 cm、5 cm、7 cm 4个测点的实测值作为已知量,按照文中的迭代方法计算其放电点深度r、衰减系数a以及放电源点信号量。通过模拟计算得到当高压尖端引到环氧套管外表面时r为0.1 cm,a值0.273, 源点信号量20.9 mV;当高压尖端引到环氧套管内表面时r为1.01 cm,a值0.275,源点信号量21.2 mV;迭代法计算的结果与实际情况基本相符。
为了进一步检验理论模型及理论分析的正确性,文中将通过迭代计算得到的放电点深度、衰减系数、源点信号量作为已知量进行仿真计算,将各测点的仿真计算结果与实测结果比较,各测点计算值及其与实测值之间的误差如表 2所示。从表中可以看出,计算结果和测量结果之间的差别很小,最大误差不超过3%,验证了理论分析的正确性。
| 表 2 理论模型计算值及与实测值之间的误差 |
在电缆终端的现场超声波局部放电带电检测过程中,有效的发现了某35 kV电缆终端的局部放电缺陷。该电缆终端为直径6 cm(不计伞裙尺寸)的干式硅橡胶电缆终端,测量结果如表 3所示。
| 表 3 某35 kV电缆终端查局部放电现场检测结果 |
根据文中的迭代法,选取其中轴向分布的0 cm、2 cm、4 cm 3个点测量值作为已知量,通过迭代计算得到放电点深度大约在0.9 cm处,衰减系数为0.309,局部放电水平1.60 mV。该终端解体后发现在最大放电信号位置电缆半导体层切割不齐, 有突出尖角, 缺陷位置深度约1 cm,按其衰减系数计算的局部放电水平为1.63 mV,与分析结果基本一致。
比较现场测量结果与实验室模拟实验结果,二者终端的类型不同、材质不同,对超声信号的衰减系数也不同,而采用文中的方法计算均得到了其放电点或缺陷的深度。
5 结论文中通过模拟计算分析了放电信号在电缆终端表面的分布规律,并由此提出了根据测得的表面放电信号分布数据通过迭代得到放电点深度及真实放电水平的分析计算方法,为超声波法在电缆检测的实际应用提供依据。通过该方法,可以根据测试结果计算出放电点的位置和放电量的大小,为放电缺陷的位置、危害程度的判断以及检修策略的制定提供技术支持。
| [1] |
鲍明晖, 尹小根, 何俊佳, 等.
高频电压下交联聚乙烯中电树枝的形态特性[J]. 中国电机工程学报, 2011, 31(34): 184–191.
BAO Minghui, YIN Xiaogen, HE Junjia, et al. Electrical tree structure characteristics in XLPE power cable insulation under high-frequency voltage[J]. Proceedings of the CSEE, 2011, 31(34): 184–191. (in Chinese) |
| [2] |
廖瑞金, 周天春, 刘玲, 等.
交联聚乙烯电力电缆电树枝生长的混沌特性分析[J]. 电工技术学报, 2012, 27(5): 63–69.
Liao Ruijin, Zhou Eanchun, Liu Ling, et al. The chaos characteristics analysis for electrical treeing propagation in XLPE power cables[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 63–69. (in Chinese) |
| [3] |
郑晓泉, ChenG, DavieA E.
交联聚乙烯电缆绝缘中的电树枝与绝缘结构亚微观缺陷[J]. 电工技术学报, 2006, 21(11): 28–33.
ZHENG Xiaoquan, Chen G, Davie A E. Electrical tree and submicroscopic insulation structure weakness in XLPE cable insulation[J]. Transactions of China Electrotechnical Society, 2006, 21(11): 28–33. DOI:10.3321/j.issn:1000-6753.2006.11.006 (in Chinese) |
| [4] |
顾金, 王俏华, 尹毅, 等.
高压直流XLPE电力电缆预制式接头的设计[J]. 高电压技术, 2009, 35(12): 3159–3163.
GU Jin, W ANG Qiaohua, YIN Yi, et al. Design of prefabricated joints for HVDC XLPE power cables[J]. High Volfage Engineering, 2009, 35(12): 3159–3163. (in Chinese) |
| [5] | Krivda A, Gulski E, Satish L, et al. The use of fractal features for recognition of 3-D discharge patterns[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1995, 2(5): 889–892. DOI:10.1109/94.469983 |
| [6] |
谢安生, 李盛涛, 郑晓泉, 等.
高频电压下交联聚乙烯电缆绝缘中电树枝生长的动力学模型[J]. 物理学报, 2008, 57(6): 3828–3833.
XIE Ansheng, LI Shengtao, ZHENG Xiaoquan, et al. Dynamics model for electrical tree propagation in cross-linked polyethylene cable insulaton under high frequency voltage[J]. Acta Physica Sinica, 2008, 57(6): 3828–3833. DOI:10.7498/aps.57.3828 (in Chinese) |
| [7] | 李盛涛, 郑晓泉. 聚合物电树枝化[M]. 北京: 机械工业出版社, 2006: 10-15. |
| [8] |
谢安生, 郑晓泉, 李盛涛.
XLPE电缆绝缘中的电树枝结构及其生长特性[J]. 高电压技术, 2007, 33(6): 168–173.
XIE Ansheng, ZHENG Xiaoquan, LI Shengtao. Structures and propagation characteristics of electrical trees in XLPE cable insulation[J]. High Voltage Engineering, 2007, 33(6): 168–173. (in Chinese) |
| [9] | Chen H C. Fractal features-based pattern recognition of partial discharge in XLPE power cables using extension method[J]. Generation Transmission & Distribution IET, 2012, 6(11): 1096–1103. |
| [10] |
郑文栋, 杨宁, 钱勇, 等.
多传感器联合检测技术在XLPE电缆附件局部放电定位中的试验研究[J]. 电力系统保护与控制, 2011, 39(20): 84–88.
ZHENG Wendong, YANG Ning, QIAN Yong, et al. Experimental research on partial discharge localization in XLPE cable accessories using multi sensor joint detection technology[J]. Power System Protection and Control, 2011, 39(20): 84–88. DOI:10.7667/j.issn.1674-3415.2011.20.015 (in Chinese) |
| [11] |
魏钢, 唐炬, 文习山, 等.
局部放电信号在交联聚乙烯高压电力电缆中的衰变及其检测[J]. 高电压技术, 2011, 37(6): 1377–1383.
WEI Gang, TANG Ju, WEN Xishan, et al. Decay and detection of partial discharge signals in high-votage cross-linked polgethylene power cable[J]. High Voltage Engineering, 2011, 37(6): 1377–1383. (in Chinese) |
| [12] |
廖瑞金, 周天春, 刘玲, 等.
交联聚乙烯电力电缆的电树枝化试验及其局部放电特征[J]. 中国电机工程学报, 2011, 31(28): 136–142.
LIAO Ruijin, ZHOU Tianchun, LIU Ling, et al. Experimentals research on electrical treeing and partial discharge characteristics of cross-linked polyethyrene power cable[J]. Proceedings of the CSEE, Proceeding of the CESS, 2011, 31(28): 136–142. (in Chinese) |
| [13] |
姜芸, 闵红, 罗俊华, 等.
220 kV电缆接头半导电尖端缺陷的局部放电试验[J]. 高电压技术, 2011, 36(11): 2657–2661.
JIANG Yun, MIN Hong, LUO Junhua, et al. Partial discharge pattern of semi-conductor layer tip defect in 220kv cable[J]. High Voltage Engineering, 2011, 36(11): 2657–2661. (in Chinese) |
| [14] |
郭灿新, 勇明, 徐敏骅, 等.
S变换在电力电缆局部放电信号时频分析中的应用[J]. 电工技术学报, 2010, 25(11): 9–14.
GUO Canxin, YONG Ming, XU Minhua, et al. Application of S transform for time-frequency analysis of partial discharge signals in power cables[J]. Transactions of China Electrotechnical Society, 2010, 25(11): 9–14. (in Chinese) |
| [15] |
姜芸, 闵虹, 夏荣, 等.
高压交联电缆接头局部放电的电容耦合法检测及分析[J]. 高电压技术, 2010, 36(8): 2005–2011.
JIANG Yun, MIN Hong, XIA Rong, et al. Capacitive coupling detection and characteristic analysis of partial discharge in high-voltage XLPE power cable joints[J]. High Voltage Engineering, 2010, 36(8): 2005–2011. (in Chinese) |
| [16] |
唐炬, 朱黎明, 龚宁涛.
高压电缆中问接头局部放电统计特性分析[J]. 重庆大学学报, 2009, 32(8): 965–970.
TANG Ju, ZHU Liming, GONG Ningtao. Statistical characteristics analysis of partial discharge in high voltage cable joint[J]. Journal of Chongqing University, 2009, 32(8): 965–970. DOI:10.11835/j.issn.1000-582X.2009.08.020 (in Chinese) |
| [17] |
唐炬, 龚宁涛, 李伟.
高压交联聚乙烯电缆附件局部放电特性分析[J]. 重庆大学学报, 2009, 32(5): 528–534.
TANG Ju, GONG Ningtao, LI Wei. Characteristic analysis of partial discharge in high voltage XLPE cable accessories[J]. Journal of Chongqing University, 2009, 32(5): 528–534. DOI:10.11835/j.issn.1000-582X.2009.05.009 (in Chinese) |
| [18] |
唐炬, 李伟, 杨浩.
高压电缆附件局部放电超高频检测与分析[J]. 高电压技术, 2009, 35(7): 1571–1577.
TANG Ju, LI Wei, YANG Hao. Ultra-high frequency detection and analysis for partial discharge in high-voltage cable accessories[J]. High Voltage Engineering, 2009, 35(7): 1571–1577. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

