超声波电机[1-3]与传统电机相比,具有结构简单、重量轻、响应速度快、噪声低、低速大转矩、断电自锁、不受磁场干扰等优点,已在许多领域得到了应用,如精密仪器仪表、航空航天、智能机器人、精密X-Y平台等。超声波电机的二相驱动输入在机械上相互耦合,因此转子二相能量转换过程中不可能完全相等,转子的二相等效负载也不可能完全相等,随工作情况的不同,其等效电路模型也会发生变化。
现有的超声波电机驱动电路,常见的有串联或者并联谐振电路、电流源并联谐振以及串并联谐振电路等,其谐振频率基本接近于电机的谐振频率[4-10]。这些电路在工作时各有优缺点。串联或者并联谐振电路容易实现,但是二相驱动电压会受到电机运行时品质因数变化的影响;而串并联谐振电路虽然不易受到电机品质因数变化的影响,但其输出电压幅度会发生变化,因此需要外接能量反馈电路加以补偿。
电机在运行时,其二相驱动电路的品质因数会发生变化,当驱动频率越接近谐振频率,驱动电路的电压增益随品质因数的变化就会越明显[11-12],这会造成电机的输入电压发生变化,并导致在相同的驱动频率下,电机二相驱动电压的不平衡,因此电机也就难以获得较好的动态性能。
与传统串联或者并联LC谐振驱动电路相比,LLCC驱动电路具有一些优势[13-15]。在高频驱动下,电路的分布电感和开关元件的结电容在设计时可以在电路中充分加以考虑;LLCC电路的电感或电容可以提高驱动电路的性能。此外,LLCC电路工作在谐振频率附近时,超声波电机二相驱动输入电压基本不受品质因数变化的影响。与串联或并联LC谐振驱动电路相比,它只增加了几个电感和电容。
1 超声波电机LLCC驱动电路超声波电机的单相等效电路模型如图 1(a)所示。Cd为压电陶瓷的电容,Lm为压电陶瓷的等效电感,Cm为压电陶瓷的等效电容,r0为压电陶瓷的等效电阻,RF表示定转子滑动损耗的等效电阻,Rr表示定转子机械损耗的等效电阻,RL表示等效负载。为了有效驱动超声波电机,驱动频率fs一般选择为Cm与Lm谐振时的机械谐振频率,其频率fs为
| $ {f_{\rm{s}}} = 1/\sqrt {{L_{\rm{m}}}{C_{\rm{m}}}} 。$ | (1) |

|
图 1 超声波电机的单相等效电路模型 |
当电机工作于谐振状态时,单相等效电路可以简化为图 1(b),其中rA表示超声波电机的A相等效负载。
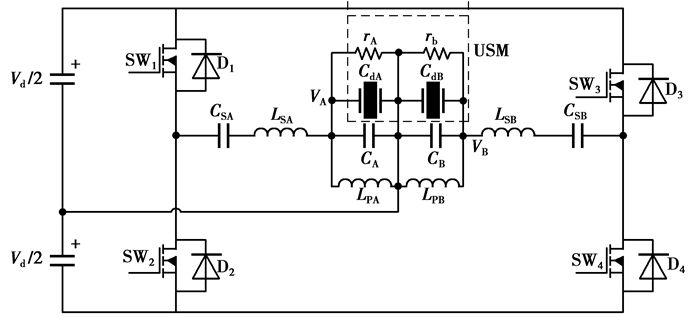
超声波电机的LLCC谐振驱动电路如图 2所示。电路由半桥电路和二相LLCC驱动电路组成,CdA、CdB为超声波电机二相输入的结电容。
|
图 2 二相半桥式LLCC谐振驱动电路 |
二相LLCC驱动电路为电机提供二相相同频率相同幅值的正弦波VA和VB,其中A相LLCC驱动电路是由一个LC (包括LSA和CSA)串联谐振电路、开关元件(SW1和SW2)和一个RLC(包括rA、LPA、CdA和CA)并联电路组成,D1和D2为反并二极管,B相的驱动电路依此类推。开关元件SW1~SW4的驱动信号由外部DSP与相应的驱动电路产生。
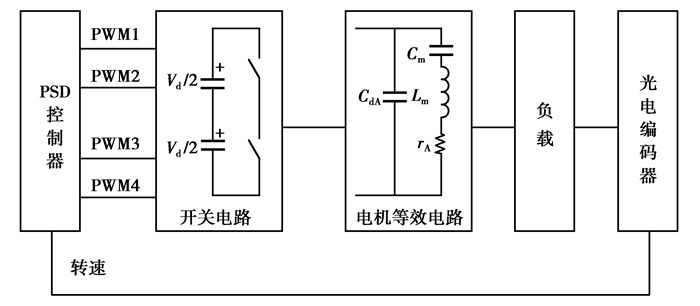
研究使用的超声波电机的工作频率为40~45 kHz。实际开关元件的工作频率略高于其机械谐振频率。开关元件的频率由DSP闭环控制,如图 3所示。
|
图 3 DSP控制系统框图 |
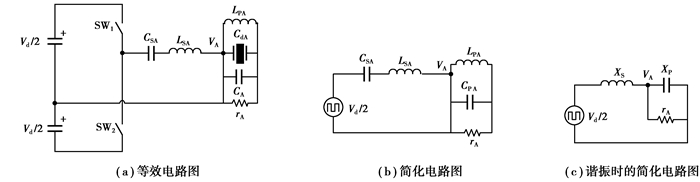
图 4(a)为LLCC驱动电路的单相等效电路图,其中SW1和SW2为MOSFET开关管,CSA为串联谐振电容,CPA为CA与CdA并联等效电容,CPA=CdA+CA。电机运行时,CdA会发生变化,CA为补偿CdA变化而外加的电容,其目的是提升电压VA的波形质量。
|
图 4 LLCC谐振电路的单相等效电路分析 |
在分析之前,先作如下假设:
1) 所有开关管和二极管均为理想器件;
2) 所有电感、电容和变压器均为理想元件;
3) 变换器采用变频控制策略,同一桥臂开关管180°互补导通;
4) 开关频率高于谐振频率,变换器工作在谐振电感电流连续模式,电感电流近似为正弦。
当电机工作于谐振状态时,其单相(如A相)驱动电路可以简化为图 4(b)。对图 4(b)来说,rA、CPA、LPA并联电路的阻抗ZP为
| $ {Z_{\rm{P}}} = {Z_{{L_{{\rm{PA}}}}}}//{Z_{{C_{{\rm{PA}}}}}}//{r_{\rm{A}}}。$ | (3) |
阻抗ZP用s域表示为
| $ {Z_{\rm{P}}}\left( s \right) = \frac{{\frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}{r_{\rm{A}}}}}{{\left( {s{L_{{\rm{PA}}}} + \frac{1}{{s{C_{{\rm{PA}}}}}}} \right){r_{\rm{A}}} + \frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}}}, $ | (4) |
式中s=jω。
LLCC谐振驱动电路的单相输入阻抗ZIN(s)为
| $ {Z_{{\rm{IN}}}}\left( s \right) = s{L_{{\rm{SA}}}} + \frac{1}{{s{C_{{\rm{SA}}}}}} + {Z_{\rm{P}}}\left( s \right), $ | (5) |
输入电压V的基波Vi为
| $ {V_i} = {V_{\rm{m}}}\sin {\omega _s}t, $ | (6) |
若输入电压V是以下形式的方波
| $ V = \left\{ {\begin{array}{*{20}{c}} {{V_{{\rm{IN}}}},0 < \omega t \le {\rm{ \mathsf{ π} ,}}}\\ { - {V_{{\rm{IN}}}},{\rm{ \mathsf{ π} }} < \omega t \le 2{\rm{ \mathsf{ π} ,}}} \end{array}} \right. $ | (7) |
则
| $ {V_{\rm{m}}} = \frac{4}{{\rm{ \mathsf{ π} }}}{V_{{\rm{IN}}}}。$ | (8) |
由图 2可以得到
LLCC谐振电路的输出电压VA为
| $ {V_{\rm{A}}} = {V_{\rm{A}}}\sin \left( {{\omega _{\rm{s}}}t + \varphi } \right), $ | (9) |
式中φ为输入输出电压基波的相位差。
传递函数GV(s)定义为
| $ {G_{\rm{V}}}\left( s \right) = \frac{{{V_{\rm{A}}}\left( s \right)}}{{{V_i}\left( s \right)}} = A\frac{{{Z_{\rm{P}}}\left( s \right)}}{{{Z_{{\rm{IN}}}}\left( s \right)}} = A\frac{{\frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}{r_{\rm{A}}}}}{{\left( {s{L_{{\rm{SA}}}} + \frac{1}{{s{C_{{\rm{SA}}}}}}} \right)\left[ {\left( {s{L_{{\rm{PA}}}} + \frac{1}{{s{C_{{\rm{PA}}}}}}} \right){r_{\rm{A}}} + \frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}} \right] + \frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}{r_{\rm{A}}}}}, $ | (10) |
式中A为传递函数的交流增益。
由s=jω,传递函数GV(s)用频域表示为
| $ {G_{\rm{V}}}\left( {j\omega } \right) = \frac{{A\frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}}}{{ - \left( {\omega {L_{{\rm{PA}}}} - \frac{1}{{\omega {C_{{\rm{PA}}}}}}} \right)\left( {\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}} \right) + \frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}} + j\frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}{r_{\rm{A}}}}}\left( {\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}} \right)}}。$ | (11) |
当电路发生谐振时,GV(jω)的幅度|GV(jω)|为最大值。定义
| $ {A_0} = \omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}, $ | (12) |
| $ {A_1} = \omega {L_{{\rm{PA}}}} - \frac{1}{{\omega {C_{{\rm{PA}}}}}}, $ | (13) |
| $ {A_2} = \frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}, $ | (14) |
则式(11)可写为
| $ {G_{\rm{V}}}\left( {j\omega } \right) = \frac{{A{A_2}}}{{{A_2} - {A_0}{A_1} + j\frac{{{A_0}{A_2}}}{{{r_A}}}}}。$ | (15) |
GV(jω)的幅度|GV(jω)|为
| $ \left| {{G_{\rm{V}}}\left( {j\omega } \right)} \right| = \frac{{A{A_2}}}{{\sqrt {{{\left( {{A_2} - {A_0}{A_1}} \right)}^2} + {{\left( {\frac{{{A_0}{A_2}}}{{{r_A}}}} \right)}^2}} }}, $ | (16) |
即
| $ \left| {{G_{\rm{V}}}\left( {j\omega } \right)} \right| = \frac{{A\frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}}}}{{\sqrt {{{\left[ {\frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}} - \left( {\omega {L_{{\rm{PA}}}} - \frac{1}{{\omega {C_{{\rm{PA}}}}}}} \right)\left( {\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}} \right)} \right]}^2} + {{\left[ {\frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}{r_{\rm{A}}}}}\left( {\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}} \right)} \right]}^2}} }}。$ | (17) |
当LLCC谐振驱动电路处于谐振状态时,传递函数分母多项式的实部为零,即式(11)分母多项式的实部为0,即
| $ - \left( {\omega {L_{{\rm{PA}}}} - \frac{1}{{\omega {C_{{\rm{PA}}}}}}} \right)\left( {\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}} \right) + \frac{{{L_{{\rm{PA}}}}}}{{{C_{{\rm{PA}}}}}} = 0。$ | (18) |
式(18)可以化简为
| $ {\omega ^4} - \frac{1}{{{L_{{\rm{SA}}}}{C_{{\rm{PA}}}}}}\left( {1 + \frac{{{C_{{\rm{PA}}}}}}{{{C_{{\rm{SA}}}}}} + \frac{{{L_{{\rm{SA}}}}}}{{{L_{{\rm{PA}}}}}}} \right){\omega ^2} + \frac{1}{{{L_{{\rm{PA}}}}{C_{{\rm{SA}}}}{L_{{\rm{SA}}}}{C_{{\rm{PA}}}}}} = 0。$ | (19) |
现定义
| $ K = \frac{1}{{{L_{{\rm{SA}}}}{C_{{\rm{PA}}}}}}\left( {1 + \frac{{{C_{{\rm{PA}}}}}}{{{C_{{\rm{SA}}}}}} + \frac{{{L_{{\rm{SA}}}}}}{{{L_{{\rm{PA}}}}}}} \right), $ | (20) |
由于方程(19)为4阶方程,一共有4个根,其中有2个根小于零,故舍去,取其大于零的2个根ω01、ω02为
| $ {\omega _{01}} = {\left[ {\frac{K}{2} + \frac{1}{2}\sqrt {{K^2} - \frac{4}{{{L_{{\rm{SA}}}}{L_{{\rm{PA}}}}{C_{{\rm{SA}}}}{C_{{\rm{PA}}}}}}} } \right]^{\frac{1}{2}}}, $ | (21) |
| $ {\omega _{02}} = {\left[ {\frac{K}{2} - \frac{1}{2}\sqrt {{K^2} - \frac{4}{{{L_{{\rm{SA}}}}{L_{{\rm{PA}}}}{C_{{\rm{SA}}}}{C_{{\rm{PA}}}}}}} } \right]^{\frac{1}{2}}}。$ | (22) |
由式(21)、(22)可知
| $ {\omega _{01}} > {\omega _{02}},且\;{K^2} - \frac{4}{{{L_{{\rm{SA}}}}{L_{{\rm{PA}}}}{C_{{\rm{SA}}}}{C_{{\rm{PA}}}}}} > 0。$ | (23) |
除此之外,定义
| $ {X_{\rm{S}}} = j\left( {\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}} \right), $ | (24) |
| $ {X_{\rm{P}}} = j\omega {L_{{\rm{PA}}}}//\frac{1}{{j\omega {C_{{\rm{PA}}}}}}, $ | (25) |
当ω=ω01时,XS等效为一个电感,XP等效为一个电容,如图 4(c)所示。当ω=ω02时,XS等效为一个电容,XP等效为一个电感。因此在ω01、ω02处有2个Q值。为了简化分析,即Q01=Q02,取
| $ \frac{{{L_{{\rm{PA}}}}}}{{{L_{{\rm{SA}}}}}} = \frac{{{C_{{\rm{SA}}}}}}{{{C_{{\rm{PA}}}}}}。$ | (26) |
定义图 4电路的品质因数Q为
| $ Q = \frac{{{r_{\rm{A}}}}}{{\left| {{X_{\rm{S}}}} \right|}} = \frac{{{r_{\rm{A}}}}}{{\left| {{\omega _0}{L_{{\rm{SA}}}} - \frac{1}{{{\omega _0}{C_{{\rm{SA}}}}}}} \right|}}, $ | (27) |
式中ω0为ω01或者ω02。
由式(27)可知Q>0,把式(27)代入式(10),传递函数GV和交流增益相位角φ可重新写为
| $ {G_V}\left( s \right) = \frac{A}{{1 + \frac{{{C_{{\rm{PA}}}}}}{{{C_{{\rm{SA}}}}}} + \frac{{{L_{{\rm{SA}}}}}}{{{L_{{\rm{PA}}}}}} - {\omega ^2}{L_{{\rm{SA}}}}{C_{{\rm{PA}}}} - \frac{1}{{{\omega ^2}{L_{{\rm{PA}}}}{C_{{\rm{SA}}}}}} + j\frac{{\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}}}{{Q\left| {{\omega _0}{L_{{\rm{SA}}}} - \frac{1}{{{\omega _0}{C_{{\rm{SA}}}}}}} \right|}}}}, $ | (28) |
| $ \varphi = - {\rm{arctan}}\frac{{\omega {L_{{\rm{SA}}}} - \frac{1}{{\omega {C_{{\rm{SA}}}}}}}}{{Q\left| {{\omega _0}{L_{{\rm{SA}}}} - \frac{1}{{{\omega _0}{C_{{\rm{SA}}}}}}} \right|\left( {1 + \frac{{{C_{{\rm{PA}}}}}}{{{C_{{\rm{SA}}}}}} + \frac{{{L_{{\rm{SA}}}}}}{{{L_{{\rm{PA}}}}}} - {\omega ^2}{L_{{\rm{SA}}}}{C_{{\rm{PA}}}} - \frac{1}{{{\omega ^2}{L_{{\rm{PA}}}}{C_{{\rm{SA}}}}}}} \right)}}。$ | (29) |
传递函数交流增益A的定义为
| $ A = {V_{\rm{A}}}/\left( {{V_{\rm{d}}}/2} \right) = \frac{4}{{\rm{ \mathsf{ π} }}}, $ | (30) |
定义几何频率ωg为
| $ {\omega _g} = \sqrt {{\omega _{01}}{\omega _{02}}} = \frac{1}{{\sqrt {{L_{{\rm{SA}}}}{C_{{\rm{SA}}}}} }}。$ | (31) |
若ω=ωg,则式(28)分母的虚部为0,实部为1,GV不受Q变化的影响,为
| $ {G_{\rm{V}}} = A = \frac{4}{{\rm{ \mathsf{ π} }}}, $ | (32) |
且XS=0。同理,相位角φ也不受Q变化的影响。因此几何频率ωg为LLCC谐振电路的理想频率。
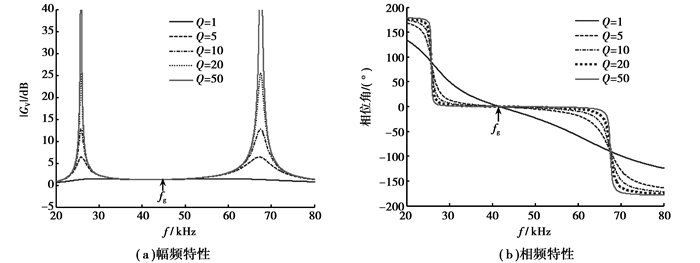
3 仿真分析研究使用的电机为ϕ60 mm行波型电机,额定转速为90 r/min,取LSA=LSB=0.66 mH,CSA=CSB=CPA=CPB=CA+CdA=22 nF,其中CdA为电机静止时的测量值,CA≈12 nF。由式(21)、(22)、(31)计算可以得到f01=25.8 kHz,f02=67.5 kHz,fg=41.8 kHz。当Q取不同值且系统的开关频率在[20, 80]kHz时,图 5(a)、(b)分别表示根据式(28)、(29)计算得到的LLCC谐振电路幅度—频率特性和相位—频率特性。由图 5可见,在整个频率变化范围内,系统的幅频特性和相频特性变化较大,|GV|最大值处的频率与几何频率相差较大;当系统的开关频率在几何频率fg附近时,即使品质因数变化较大,谐振电路的幅频特性和相频特性变化也不大。当工作频率在39~45 kHz之间变化,图 5中的一部分经放大后在图 6中显示。在工作频率变化范围内,图 6(a)所示的幅度—频率特性变化范围小于3%。另一方面,超声波电机工作时其驱动系统的品质因数一般都大于10,由图 6(b)可以知道驱动系统的相位变化范围小于2°。由以上结果可知,使用LLCC驱动电路的超声波电机在运行时可以获得较好的动态性能。
|
图 5 LLCC谐振电路的幅频特性和相频特性 |
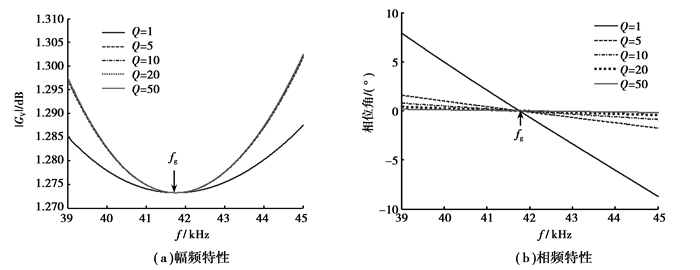
|
图 6 LLCC谐振电路的幅频特性和相频特性 |
当电机转速为60 r/min时,经测试其电容CdA、CdB变为10.4 nF,由此可以得到图 7(a)、(b)所示的幅度—频率特性和相位—频率特性。从图 7可见,当品质因数Q变化范围较大时,电机在几何频率附近的幅频特性和相频特性变化小于3.5%。因此,当超声波电机工作导致等效电路参数变化时,电机也可以保持较好的动态性能。
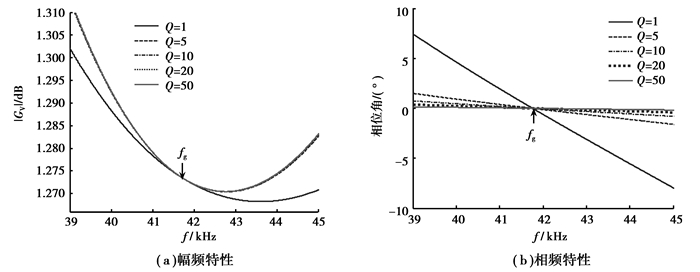
|
图 7 参数变化时LLCC谐振电路的幅频特性和相频特性 |
实验使用的电机为ϕ60 mm行波型超声波电机,半桥电路的输入电压Vd=150 V DC。图 8为驱动装置实物图,图 9~图 10中VA、VB为电机二相驱动电压,UDS为开关元件漏极与源极的电压差(即半桥电路的输入电压)。图 9是开关频率fs设为41.9 kHz时LLCC驱动电路的输出波形,图 9(a)中驱动电压VA落后驱动电压VB为90°,此时转速为91 r/min,驱动电压峰峰值VPP为394 V;图 9(b)中驱动电压VA超前驱动电压VB为90°,此时转速为90 r/min,驱动电压峰峰值VPP为390 V,此时VA与半桥电路输入电压的相位差在1°以内。

|
图 8 LLCC驱动装置实物图 |
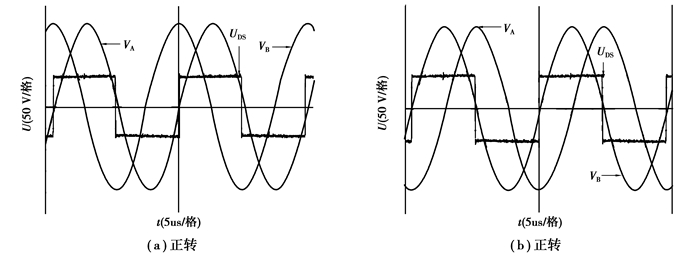
|
图 9 fs为41.9 kHz时驱动电路输出波形 |
图 10为fs取42.8 kHz且电机带0.1 N·m负载时驱动电路的输出波形。图 10(a)中驱动电压VA落后驱动电压VB为90°,此时转速为62 r/min,驱动电压峰峰值VPP为392 V。图 10(b)中驱动电压VA超前驱动电压VB为90°,此时转速为61 r/min,驱动电压峰峰值VPP为394 V。由图 9~图 10可见,其二相驱动电压VA、VB基本相等,即驱动电压只由半桥电路的输入电压Vd控制,而且满足式(32),交流增益相位角与理论计算基本一致。
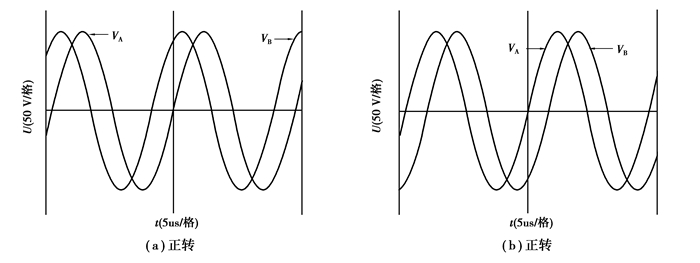
|
图 10 fs为42.8 kHz时驱动电路输出波形 |
在不同驱动频率下经测算得到的品质因数如表 1所示。
| 表 1 不同频率时的品质因数 |
从超声波电机的LLCC驱动电路出发,分析了LLCC驱动电路的等效电路,并从数学上得到其传递函数,证明LLCC驱动电路不受频率、品质因数和负载变化的影响。通过仿真和实验,验证了实验结果与理论分析基本一致:在LLCC驱动电路的几何频率附近区间内,驱动电路输出电压的幅度不受电路品质因数变化的影响,保持为固定数值,实验结果也验证了此电路的有效性。此驱动电路为超声波电机驱动提供了一种有效的思路,为电机控制性能的提升打下了基础。
| [1] | 赵淳生. 超声电机技术与应用[M]. 北京: 科学出版社, 2007. |
| [2] | Mashimo T, Toyama S, Ishida H. Design and implementation of spherical ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2009, 56(11): 2514–2521. DOI:10.1109/TUFFC.2009.1338 |
| [3] |
胡锡幸, 郭吉丰.
3个行波定子的2自由度球形超声波电机[J]. 中国电机工程学报, 2010, 30(9): 62–67.
HU Xixing, GUO Jifeng. Two degree of freedom spherical ultrasonic motor with three eraveling-wave stators[J]. Proceedings of the CSEE, 2010, 30(9): 62–67. (in Chinese) |
| [4] | Shi J Z, Zhao F J, Shen X X, et al. Chaotic operation and chaos control of travelling wave ultrasonic motor[J]. Ultrasonics, 2013, 53(6): 1112–1123. DOI:10.1016/j.ultras.2013.02.006 |
| [5] | Nagata F, Ogiwara K, Watanabe K. Basic position/force control of a single-axis arm designed with an ultrasonic motor[J]. Artificial Life and Robotics, 2011, 16(1): 102–106. DOI:10.1007/s10015-011-0898-8 |
| [6] | Odomari S, Hieu N T, Uchida K, et al. Robust position control for ultrasonic motor using variable structure system observer in non-linear observer[J]. Electric Power Components and Systems, 2011, 39(16): 1769–1782. DOI:10.1080/15325008.2011.615794 |
| [7] | Cheng F, Fan K C, MiaoJ W, et al. A bpnn-pid based long-stroke nanopositioning control scheme driven by ultrasonic motor[J]. Precision Engineering, 2012, 36(3): 485–493. DOI:10.1016/j.precisioneng.2012.03.001 |
| [8] | Shi J Z, Liu B. Non-linear generalized predictive control of traveling-wave ultrasonic motor[J]. Electric Power Components and Systems, 2012, 40(3): 485–493. |
| [9] | Boukhnifer M. Active fault tolerant control for ultrasonic piezoelectric[J]. Journal of Electrical Engineering, 2012, 63(4): 224–232. |
| [10] |
顾菊平, 胡敏强.
超声波电机谐振升压式驱动技术研究[J]. 中国电机工程学报, 2002, 22(8): 49–52.
GU Juping, HU Minqiang. Research on the resonant booster of ultrasonic motor driving[J]. Proceedings of the CSEE, 2002, 22(8): 49–52. (in Chinese) |
| [11] |
李华峰, 赵淳生.
基于LC谐振的超声电机驱动器的研究[J]. 中国电机工程学报, 2005, 25(23): 145–147.
LI Huafeng, ZHAO Chunsheng. Research on the ultrasonic motor driver based on LC resonan[J]. Proceedings of the CSEE, 2005, 25(23): 145–147. (in Chinese) |
| [12] | Yu M L, Huang X J. Control of ultrasonic motor based on DSP[J]. International Journal of Advances in Engineering and Technology, 2013, 6(3): 1049–1054. |
| [13] |
傅平.
基于LCC的超声波电机驱动电路分析[J]. 微特电机, 2012, 40(9): 59–62.
FU Ping. Analysis of driving circuit for ultrasonic motor based on LCC[J]. Small & Special Electrical Machines, 2012, 40(9): 59–62. (in Chinese) |
| [14] |
韩力, 罗杰, 王华, 等.
无刷双馈电机稳态数学模型和运行特性分析[J]. 重庆大学学报, 2013, 36(8): 61–67.
HAN Li, LUO Jie, WANG Hua, et al. Analysis on steady-state mathematical models and operating characteristics of brushless doubly-fed machine[J]. Journal of Chongqing University, 2013, 36(8): 61–67. DOI:10.11835/j.issn.1000-582X.2013.08.010 (in Chinese) |
| [15] |
罗辞勇, 张帆, 杜劲超.
行波型超声电机的稳定性分析[J]. 重庆大学学报, 2014, 37(2): 46–53.
LUO Ciyong, ZHANG Fan, DU Jinchao. Stability study of the traveling wave ultrasonic motor[J]. Journal of Chongqing University, 2014, 37(2): 46–53. DOI:10.11835/j.issn.1008-5831.2014.02.007 (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


