b. 深圳大学 机电与控制工程学院, 广东 深圳 518060
b. College of Mechatronic and Control Engineering, Shenzhen University, Shenzhen, Guangdong 518060, China
DC潮流因关系简明且无收敛问题而在现代智能电网规划和运行中得到广泛应用,如:基于DC潮流的最优潮流(OPF)问题,包括日前和实时安全约束经济调度(或发电计划)[1-5]、节点电价计算与分解[5-12]、日前发电计划的安全校核[13-15]、实时阻塞管理[16]等。为弥补DC潮流未计入网损导致电力系统运行经济性低下的缺陷,先进的基于DC潮流的OPF都引入了网损模拟[5-6, 11]。已有基于DC潮流并模拟网损的OPF,其所得电价的解对参考节点的依赖性已有共识结论:“存在依赖性”[7-9],但所得发电功率的解对参考节点的依赖性至今鲜见研究报道。
基于DC潮流的有损OPF中,网损的模拟方法主要有潮流雅可比逆阵法(丢参考节点)和B系数法2种。用B系数模拟网损的基于DC潮流的OPF,因B系数事先由基态潮流求得,不能有效跟踪待求最优潮流。它至上世纪末已淡出应用,文中不予讨论。
用潮流雅可比逆阵模拟网损的基于DC潮流的OPF,网损被表达成基于潮流雅可比逆阵的发电机功率的函数。潮流雅可比逆阵在DC潮流下是常数阵、交流潮流下可由实时状态估计潮流收敛时的因子表求得,不仅算速快、而且能有效跟踪待求最优潮流。因此,用潮流雅可比逆阵模拟网损的OPF得到了广泛工程应用,是文中讨论的对象。
用潮流雅可比逆阵模拟网损的基于DC潮流的OPF,自上世纪70年代Podmore提出并用于发电调度以来,模型并无实质发展。但电力市场的出现使它的工程应用及研究更加生机勃勃[5-16],同时也使其解对参考节点的依赖性问题更加凸现。
文献[1]中式(2)本质上是基于DC潮流雅可比逆阵将网损表达成发电机功率的函数,再用于发电竞价(或发电调度),原型上构成用潮流雅可比逆阵模拟网损的基于DC潮流的OPF。文献[1]简要分析得到:这种OPF所得发电功率的解对参考节点无依赖性。Wood等人基于交流潮流雅可比逆阵模拟网损也用于经济调度,得到同样结论。
文献[6]报道了ISO New England的工程实践:基于式(8)中潮流雅可比逆阵将网损表达成发电机功率的函数、建立基于DC潮流的OPF模型,用于发电调度和电价分解。其示例结果表明,采用潮流雅可比逆阵模拟网损的基于DC潮流的OPF,所得发电功率的解随参考节点变化产生的偏差达2.5%,发电功率的解对参考节点有依赖性。
文献[1, 6]都是用潮流雅可比逆阵模拟网损的基于DC潮流的OPF,但给出的结论却相反:前者“发电功率的解不依赖参考节点”、后者“发电功率的解依赖参考节点”。因此,有必要深入研究这种OPF的解对参考节点的依赖性。
文中先基于DC潮流的雅可比逆阵构建网损的直接模拟公式,再构建基于DC潮流并直接模拟网损的OPF模型,然后通过仿真就这种OPF所得发电功率的解对参考节点的依赖性展开深入研究。
1 基于DC潮流雅可比逆阵的直接网损模拟公式对有n个节点(含Vθ参考节点、不含大地节点)的电网,参考节点编号为1时,在下述DC潮流假定条件下:
1) 各节点电压幅值等于1.0 pu;
2) 线路电抗xij远大于线路电阻rij,以至线路导纳gij+jbij =1/(rij+jxij)≈0-j1/xij;
3) 节点i和j的电压相位差θi-θj很小,以至cos(θi-θj)≈1、sin(θi-θj)≈θi-θj,电网的交流潮流方程简化为下述DC潮流方程(无功方程不复存在):
| $ \left( {\begin{array}{*{20}{c}} {{P_2} - {D_2}}\\ \vdots \\ {{P_n} - {D_n}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \begin{array}{l} - \sum\limits_{k \in 2} {{b_{2k}}} \\ \vdots \\ {b_{n2}} \end{array}&\begin{array}{l} \cdots \\ \\ \cdots \end{array}&\begin{array}{l} {b_{2n}}\\ \vdots \\ - \sum\limits_{k \in n} {{b_{nk}}} \end{array} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\theta _2}}\\ \vdots \\ {{\theta _n}} \end{array}} \right) = \mathit{\boldsymbol{B'}}\left( {\begin{array}{*{20}{c}} {{\theta _2}}\\ \vdots \\ {{\theta _n}} \end{array}} \right), $ | (1) |
其中:Pk和Dk及θk分别是k节点的发电有功和负荷有功及电压相位;bij是线路i-j的电纳。DC潮流方程(1)的左边是节点注入功率向量[P2-D2 P3-D3 … Pn-Dn]T,右边的矩阵积是该向量的函数式、其变元是向量[θ2 θ3 … θn]T。按向量微积分中雅可比矩阵的通用标准定义,DC潮流方程(1)的雅可比矩阵就是DC潮流方程的系数矩阵、即“式(1)第一个等号右边的方阵或B ′”,它丢掉了参考节点的DC潮流方程对应的行和列。
按功率定义,导纳为gij+jbij的支路ij上,精确有功损耗为gij(Vi2+Vj2-2ViVj cosθij)。运用DC潮流假定条件(1),得电网总损耗
| $ L = \sum\limits_{ij} {{g_{ij}}{{\left( {{\theta _i} - {\theta _j}} \right)}^2}} 。$ | (2) |
方程(1)等号两边左乘B′-1后代入(2)消去θ得
| $ L = \sum\limits_{k = 2}^n {\sum\limits_{i = 2}^n {{\beta _{ki}}\left( {{P_k} - {D_k}} \right)\left( {{P_i} - {D_i}} \right)} } , $ | (3) |
其中βki是消去θ时产生的系数、由B′-1和gij决定。
式(3)是基于DC潮流雅可比逆阵B′-1直接导得的,简称为网损的潮流雅可比逆阵直接模拟公式。须指出的是:文献[11]基于发电转移系数表达网损,而该系数必须从忽略线路电阻的B′-1求得,故其网损公式是式(3)的近似;文献[5-6]基于网损灵敏度表达网损,而该灵敏度必须用潮流雅可比逆阵求得(需要基点潮流),直流潮流下[5-6]的网损公式可由式(3)派生。
2 基于DC潮流并直接模拟网损的OPF模型由于理想的发电成本函数是发电机功率的二次函数,再考虑线路潮流极限约束和发电机出力上下限,并用式(1)的变形和(2)等价替代式(3)模拟网损,得到基于DC潮流并直接模拟网损的OPF模型:
| $ \min F = \sum\limits_{k = 1}^n {\left( {{a_k}P_k^2 + {b_k}{P_k} + {c_k}} \right)} , $ | (4) |
| $ {\rm{S}}{\rm{.t}}{\rm{.}}\;\;\;\sum\limits_{k = 1}^n {{D_k} + L} - \sum\limits_{k = 1}^n {{P_k} = 0} , $ | (5) |
| $ L = \sum\limits_{ij} {{g_{ij}}{{\left( {{\theta _i} - {\theta _j}} \right)}^2}} , $ | (6) |
| $ \left| {{b_{ij}}\left( {{\theta _i} - {\theta _j}} \right)} \right| \le P_{ij}^u,ij \in \left\{ {lines} \right\}, $ | (7) |
| $ P_k^l \le {P_k} \le P_k^u,k \in \left\{ {1,2 \cdots ,n} \right\}, $ | (8) |
| $ \left( {\begin{array}{*{20}{c}} {{\theta _2}}\\ \vdots \\ {{\theta _n}} \end{array}} \right) = {B^{' - 1}}\left( {\begin{array}{*{20}{c}} {{P_2} - {D_2}}\\ \vdots \\ {{P_n} - {D_n}} \end{array}} \right), $ | (9) |
其中ak、bk和ck是k节点发电机的发电成本系数,式(4)表示以最小化系统发电成本F为目标函数。式(5)是系统有功平衡方程。式(7)是线路ij有功潮流的极限(用Piju表示)约束。式(8)是发电机功率的下限Pkl和上限Pku约束。对DC潮流方程(1),B′既是其系数矩阵、又是其雅可比矩阵,为方便,文中称式(1)变形后的式(9)为直流潮流雅可比矩阵方程。
必须指出:文献[5-6]中DCOPF模型的构建都需要先基于基点潮流求雅可比逆阵、继而求模拟网损用的网损灵敏度,其模型构建需要基点潮流。模型(4)~(9)的构建却无需基点潮流,这为研究一类OPF的解对参考节点的依赖性提供了极大便利,这正是文中构建模型(4)~(9)的原因。目的是最终改进传统DCOPF模型、消除其解对参考节点的依赖性。
3 仿真与分析 3.1 仿真算例就模型(4)~(9)对IEEE 14-、30-、118-bus系统等进行了仿真。限于篇幅,下面只给出三节点系统在不同参考节点下的仿真结果与分析(如图 1所示)。
|
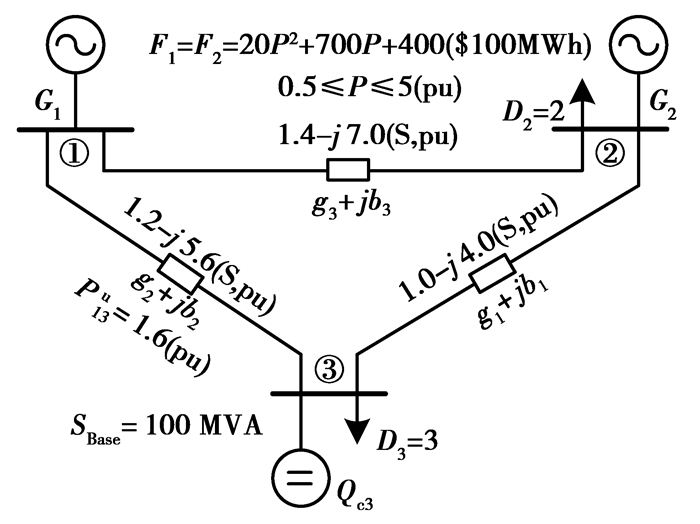
图 1 三节点系统 |
图 1中的电网结构和运行参数都是标么值。节点2和3的负荷复功率分别为2+j0.7和3+j1(图中只标出其有功D2和D3)。2台发电机的给定出力范围都是[0.5,5],且上限等于总负荷,这样给限值的目的,是为了让参考节点对“基于DC潮流并直接模拟网损的OPF的解”的影响得到充分展现。
由图 1中2台发电机的成本函数、线路1-3潮流上限P13u=1.6 pu、2个节点的负荷有功,有基于DC潮流并直接模拟网损的OPF模型(4)~(9)的具体形式:
| $ \min F = 20P_1^2 + 20P_2^2 + 700{P_1} + 700{P_2} + 800, $ | (10) |
| $ S.t.5 + L - {P_1} - {P_2} = 0, $ | (11) |
| $ 1.4{\left( {{\theta _1} - {\theta _2}} \right)^2} + 1.2{\left( {{\theta _1} - {\theta _3}} \right)^2} + {\left( {{\theta _2} - {\theta _3}} \right)^2} - L = 0, $ | (12) |
| $ 1.6 - 5.6\left( {{\theta _1} - {\theta _3}} \right) \ge 0, $ | (13) |
| $ 0.5 \le {P_k} \le 5,k \in \left\{ {1,2} \right\}。$ | (14) |
节点1作相位参考时,θ1=0、式(9)具体为
| $ \left( {\begin{array}{*{20}{c}} {{\theta _2}}\\ {{\theta _3}} \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} {11}&{ - 4}\\ { - 4}&{9.6} \end{array}} \right)^{ - 1}}\left( {\begin{array}{*{20}{c}} {{P_2} - {D_2}}\\ { - {D_3}} \end{array}} \right)。$ | (15) |
节点2作相位参考时,θ2=0、式(9)具体为
| $ \left( {\begin{array}{*{20}{c}} {{\theta _1}}\\ {{\theta _3}} \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} {12.6}&{ - 5.6}\\ { - 5.6}&{9.6} \end{array}} \right)^{ - 1}}\left( {\begin{array}{*{20}{c}} {{P_1}}\\ { - {D_3}} \end{array}} \right)。$ | (16) |
节点3作相位参考时,θ3=0、式(9)具体为
| $ \left( {\begin{array}{*{20}{c}} {{\theta _1}}\\ {{\theta _2}} \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} {12.6}&{ - 7}\\ { - 7}&{11} \end{array}} \right)^{ - 1}}\left( {\begin{array}{*{20}{c}} {{P_1}}\\ {{P_2} - {D_2}} \end{array}} \right)。$ | (17) |
式(10)~式(14)分别与式(15)、式(16)、式(17)构成以节点1、2、3为参考节点的基于DC潮流并直接模拟网损的OPF模型。
3.2 仿真结果与分析对式(10)~式(14)分别与式(15)、式(16)、式(17)构成的基于DC潮流并直接模拟网损的OPF模型,运用内点法求解[17]。考虑到应用中可能不计线路潮流极限约束,表 1和表 2给出了不计入和计入线路1-3潮流极限约束2种情况下的OPF仿真结果。
| 表 1 不计入线路潮流极限的OPF结果 |
| 表 2 计入线路潮流极限的OPF结果 |
不计线路1-3潮流极限约束的OPF,参考节点变化时:引起电价λS相对偏移高达19.13%、影响度最大,引起各节点发电功率相对偏移高达2.90%、影响度居中,引起系统总发电成本相对偏移达0.67%、影响度最小。因此,基于DC潮流并直接模拟网损的OPF,不仅所得发电功率的解、而且所得其他变量的解,都对参考节点有依赖性。
计入线路1-3潮流极限约束的OPF,参考节点变化时:引起电价λS相对偏移高达308.37%、影响度最大,引起各节点发电功率相对偏移高达125.47%、影响度次之,引起系统总发电成本相对偏移达3.59%、影响度最小。同样,基于DC潮流并直接模拟网损的OPF,不仅所得发电功率的解、而且所得其他变量的解,都对参考节点有依赖性。
上面给出的是“参考节点变化、负荷水平不变”时的结果。显然,若模型本身不存在参考节点依赖性,则结果唯一、负荷变动小时结果变化也小。
对比表 1和表 2的第5(或第6)列:不管哪个节点作相位参考,线路1-3潮流极限约束的出现都导致网损(或发电成本)增大,这是因为此时的电网潮流需按发电成本最小重新分布、以致潮流分布均匀性劣化的缘故。显然,若2台机组的发电成本不同,线路潮流极限约束的出现还导致低(高)成本机组减(增)出力。
比较表 1和表 2,线路1-3上的潮流从无极限约束到有极限约束变化时,引起发电功率(系统电价、网损、发电成本)相对偏移情况如下:Bus 1作参考时为77.97%(5.68%、4.09%、1.42%),Bus 2作参考时为106.97%(6.08%、2.74%、1.87%),Bus 3作参考时为296.80%(224.36%、20.43%、4.36%),是3种参考节点下偏移最大的情况。线路1-3潮流极限约束的出现对发电功率的解影响最大(偏移高达296.80%),对其他变量的解影响也很显著。因此,基于DC潮流并直接模拟网损的OPF,不仅所得发电功率的解、而且所得其他变量的解,都对线路潮流极限约束很敏感。
对IEEE 14-、30-、118-bus系统等仿真,其结果的结论同上。
综上所述,基于DC潮流并直接模拟网损的OPF所得发电功率的解,不仅对参考节点有依赖性、而且这种依赖性对线路潮流极限约束很敏感。因此,该结论对电价、网损、发电成本的解也成立。这进一步验证了电价解的参考节点依赖性共识。
该结论是基于模型(4)~(9)的大量仿真结果得到的。由于模型(4)~(9)是带不等式约束的非线性规划,数学上尚无解析方法证明上述结论。
4 用B′-1直接模拟网损的OPF依赖参考节点的根源从模型结构看:式(10)~式(14)分别与式(15)、式(16)、式(17)构成以节点1、2、3为参考节点的用B′-1直接模拟网损的OPF模型。比较这些模型的结构,其差异仅在于雅可比矩阵方程(9):选节点k(=1、2、3)作相位参考时,是丢k节点的雅可比矩阵方程。用B′-1直接模拟网损的OPF模型(4)~(9),其结果依赖参考节点的主要结构性根源,是模型中采用了丢参考节点的雅可比矩阵方程。之所以说是“主要结构性根源”,是因为“式(9)所述网络无损耗与式(5)所述网络有损耗的情况导致网损累加到参考节点”是次要结构性根源,它导致OPF所得发电方案也随参考节点变化,但变化值小于网损(21.73~30.83 MW)。表 2中,OPF所得发电方案随参考节点的变化值P1达到76.58 MW,是网损的2~3倍多,这表明模型中采用丢参考节点的雅可比矩阵方程才是导致参考节点依赖性的主要结构性根源。
从模型意义看:雅可比矩阵方程(9)中,右边不含参考节点的发电和负荷功率,左边不含参考节点的电压相位。其物理意义为:参考节点的功率对非参考节点电压相位的影响恒等于零。对式(6)和式(7)为:参考节点的功率对网损和线路潮流的影响恒等于零。这正是参考节点变化导致OPF结果变化的中间过程体现。
从电路原理看:模型(4)~(9)中,采用丢参考节点的雅可比矩阵方程(9),等价于用参考节点对地短路电网的电气量关系替代原始电网的电气量关系。这种替代并不等于按电路原理做消去参考节点运算的效果、参考节点的电源未被移植到被保留电网。从叠加原理看,这等于丢掉了参考节点电源激励产生的响应的叠加。这正是模型(4)~(9)依赖参考节点的原理性缺陷。
5 电力网欠秩问题根据上节分析,基于DC潮流并直接模拟网损的OPF,其结果依赖参考节点的主要根源,是模型中采用了丢参考节点的雅可比矩阵方程,这导致用参考节点对地短路电网的电气量关系替代原始电网的电气量关系。因此,只有OPF模型中采用包括参考节点的全节点雅可比矩阵方程,才能消除模型的解对参考节点的依赖性。但事情并非如此简单,因为电力系统DC潮流的全节点雅可比矩阵总是奇异或病态的(对应无或有线路对地电纳的情况),这是电力系统常识。奇异时矩阵不可逆、问题不可解。病态时,若将该雅可比矩阵用于系统调控,则小扰动导致模型产生大偏差解、结果不可用。
DC潮流全节点雅可比矩阵奇异或病态,实质上就是其秩小于其维数。文中称这种特性为全节点雅可比矩阵的欠秩特性。
定义 模型或结果表达式中含全节点雅可比矩阵的规划运行控制问题,称为电力网欠秩问题。
电力网欠秩问题,是定义在模型和结果层面的问题。电力系统中的许多问题,如:当前北美电力市场日前和实时发电调度、节点电价计算与分解等问题,其模型本质上都含全节点雅可比矩阵,因此都属于欠秩问题。表 3归纳了一些典型电力网欠秩问题。
| 表 3 典型电力网欠秩问题 |
无论模型欠秩问题还是结果欠秩问题,在当前已有电力系统理论范畴内,一律都基于丢参考节点的雅可比矩阵建立近似问题模型求解,结果都对参考节点有依赖性、不唯一。这种近似方法在物理本质上是“用参考节点对地短路电网的电气量关系替代原始电网电气量关系”。所得解不符合电路电磁场中的唯一性定理(给定边界条件,如节点注入功率或电压,电路的解总是存在且唯一),应用时不仅导致系统经济性能低,而且导致安全调控时调节次数多、效能低。
如何系统求解电力网欠秩问题,是消除已有近似模型法导致的参考节点依赖性的根本,是提高电力系统调控效能的关键。
6 结论基于DC潮流并直接模拟网损的OPF所得发电功率的解,不仅对参考节点有依赖性、而且这种依赖性对线路潮流极限约束很敏感。
用潮流雅可比逆阵直接模拟网损的OPF,结果依赖参考节点的主要根源,是模型中采用了丢参考节点的雅可比矩阵方程、导致“用参考节点对地短路电网的电气量关系替代原始电网电气量关系”的原理性缺陷。
有/无线路对地电纳的电网,其全节点雅可比矩阵总是病态或奇异。这使电力网欠秩问题的已有解法都借助丢参考节点的雅可比矩阵建立近似问题模型求解,其结果都对参考节点有依赖性、应用效能低。电力网欠秩问题的系统求解方法值得深入研究。
| [1] | Zhang Y, Yu E.The research of the reference node in the calculation of network loss modification[C]//Proceedings of the2010 IEEE International Conference on Power System Technology, October 24-28, 2010, Hangzhou, China.Piscataway:IEEE Press, 2010:1-6. |
| [2] |
冯冬涵, 甘德强, 钟金, 等.
电力市场出清电价的非惟一性及定价新方法[J]. 电力系统自动化, 2006, 30(12): 27–32.
FENG Donghan, GAN Deqiang, ZHONG Jin, et al. Pricing when market optimization has multiple dual solutions[J]. Automation of Electric Power Systems, 2006, 30(12): 27–32. DOI:10.3321/j.issn:1000-1026.2006.12.006 (in Chinese) |
| [3] |
徐帆, 耿建, 姚建国, 等.
安全约束经济调度建模及应用[J]. 电网技术, 2010, 34(11): 55–58.
XU Fan, GENG Jian, YAO Jianguo, et al. Modeling and application of security constrained economic dispatch[J]. Power System Technology, 2010, 34(11): 55–58. (in Chinese) |
| [4] |
杨争林, 唐国庆.
全周期变时段"三公"调度发电计划优化模型[J]. 电网技术, 2011, 35(2): 132–136.
YANG Zhenglin, TANG Guoqing. A generation scheduling optimization model suitable to complete period and variable intervals and conforming to principles of openness, equity and justness[J]. Power System Technology, 2011, 35(2): 132–136. (in Chinese) |
| [5] | PJM Interconnection LLC.Marginal Losses Implementation FAQ[EB/OL].Pennsylvania:PJM Web Site, April 27, 2007.http://www.pjm.com. |
| [6] | Litvinov E, Zheng T, Rosenwald G, et al. Marginal loss modeling in LMP calculation[J]. IEEE Transaction on Power Systems, 2004, 19(2): 880–888. DOI:10.1109/TPWRS.2004.825894 |
| [7] |
陈之栩, 张粒子, 舒隽.
交直流迭代法求解含网损节点边际电价[J]. 电力系统自动化, 2007, 31(11): 22–25.
CHEN Zixu, ZHANG Lizhi, SHU Juan. AC-DC iterative methods for calculating locational marginal price with losses[J]. Automation of Electric Power Systems, 2007, 31(11): 22–25. DOI:10.3321/j.issn:1000-1026.2007.11.005 (in Chinese) |
| [8] | Wu T, Alaywan Z, Papalexopoulos A D. Locational marginal price calculations using the distributed-slack power-flow formulation[J]. IEEE Transaction on Power Systems, 2005, 20(2): 1188–1190. DOI:10.1109/TPWRS.2005.846156 |
| [9] | Peng J C, Jiang H, Xu G, et al. Independent marginal losses with application to locational marginal price calculation[J]. IET Gener Transm Distrib, 2009, 3(7): 679–689. DOI:10.1049/iet-gtd.2008.0551 |
| [10] | Orfanogianni T, Gross G. A general formulation for LMP evaluation[J]. IEEE Transaction On Power Systems, 2007, 22(3): 1163–1173. DOI:10.1109/TPWRS.2007.901297 |
| [11] | Li FX, Bo R.DCOPF-based LMP simulation:Algorithm, comparison with ACOPF, and sensitivity[C]//Proceedings of 2008 IEEE Transmission and DIistribution Conference and Exposition, April 21-24, Chicago, IL.PiscatawayL IEEE Press, 2007:1. |
| [12] |
王欣星, 周晖.
基于原-对偶内点法的节点边际电价计算[J]. 电网技术, 2007, 31(18): 23–27.
WANG Xinxing, ZHOU Hui. Calculation of locational marginal price based on primal-dual interior point method[J]. Power System Technology, 2007, 31(18): 23–27. (in Chinese) |
| [13] |
夏叶, 康重庆, 宁波, 等.
用户侧互动模式下发用电一体化静态安全校核[J]. 电力系统自动化, 2012, 36(9): 35–41.
XIA Ye, KANG Chongqing, NING Bo, et al. Generation and load integrated static security checking on interaction model on customer side[J]. Automation of Electric Power Systems, 2012, 36(9): 35–41. (in Chinese) |
| [14] |
王海超, 刘充许, 宋祥春, 等.
短期电能计划安全校正软约束模型[J]. 电网技术, 2011, 35(9): 111–114.
WANG Haichao, LIU Chongxu, SONG Xiangchun, et al. Security correction model with soft constraints for short-term energy scheduling[J]. Power System Technology, 2011, 35(9): 111–114. (in Chinese) |
| [15] |
汪洋, 夏清, 康重庆.
考虑电网N-1闭环安全校核的最优安全发电计划[J]. 中国电机工程学报, 2011, 31(10): 39–45.
WANG Yang, XIA Qing, KANG Chongqing. Optimal security constrained generation scheduling considering closed-loop N-1 security correction[J]. Proceedings of the CSEE, 2011, 31(10): 39–45. (in Chinese) |
| [16] |
张哲, 江长明, 许晓菲, 等.
基于节点电价的阻塞管理理论在华北电网的应用[J]. 电网技术, 2008, 32(6): 81–86.
ZHANG Zhe, JIANG Changming, XU Xiaofei, et al. Application of location marginal price based congestion management theory in north China power grid[J]. Power System Technology, 2008, 32(6): 81–86. (in Chinese) |
| [17] |
刘方, 颜伟, 徐国禹.
动态最优潮流的预测/校正解耦内点法[J]. 电力系统自动化, 2007, 31(14): 38–42.
LIU Fang, YAN Wei, XU Guoyu. Dynamic optimal power flow with decomposed predictor-corrector interior point method[J]. Automation of Electric Power Systems, 2007, 31(14): 38–42. DOI:10.3321/j.issn:1000-1026.2007.14.007 (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


