扭转梁悬架由于结构简单、制造成本低且安装方便而在轿车的后悬架中被广泛使用[1-4]。扭转梁式悬架由2个纵向摆臂和1个弹性扭转梁组成。2个纵臂分别通过橡胶衬套与车身相连,扭梁在2个车轮跳动时起到稳定杆的作用。目前主要采用刚柔耦合模型、等效动力学等方法研究扭转梁悬架的结构参数与悬架运动特性的关系、同时优化结构参数。文献[5]在ADAMS环境下对比分析了2种扭转梁悬架建模方法的特点。文献[6]建立了包含扭转梁悬架的8自由度车辆瞬态侧倾模型,分析了扭转梁悬架系统对瞬态侧倾的影响。文献[1]通过构建后扭转梁多体仿真模型,并在此基础上研究了扭转梁悬架横梁开口角度对前束变化,侧倾中心高度等悬架参数以及整车侧倾角的影响。文献[7]在建立扭转梁模型的基础上研究了横梁开口方向、位置,衬套安装角度等参数与悬架性能之间的关系,并计算了这些参数对悬架K & C特性指标的灵敏度。上述研究使用不同的方法分析了扭转梁悬架的衬套安装角度等设计参数对悬架性能的影响,但是仅对比分析得出了设计参数为某几个特殊值时的情况,没能在设计参数的整个设计空间之内,找出悬架特性与设计参数的非线性关系。文献[10]通过建立目标函数,把多目标问题转化为单目标问题对悬架衬套安装角度和C特性指标进行了优化,但是由于没有分析衬套安装角度对悬架C特性影响的规律,这增加了优化目标确定的难度和优化偏差,并且未能实现悬架性能和整车操稳性能的协同优化。因此,文中将利用多体动力学软件ADAMS建立扭转梁悬架的刚柔耦合样机模型,并结合Isight软件,详细研究纵臂与车身相连的衬套安装角度对扭转梁悬架性能和整车操稳性能的影响,探明悬架K & C特性及整车的操稳性能指标与衬套安装角度在整个设计空间的非线性关系,得出对各性能指标最敏感的衬套安装角度。并基于上述分析,通过遗传算法来实现衬套安装角度和整车操稳性指标的多目标协同优化,为悬架衬套安装角度的设计提供理论依据。
1 扭转梁模型的建立为了模拟扭转梁的变形,文中扭转梁采用柔性体建立。如图 1所示为文中建立的扭转梁后悬架刚柔耦合模型[8-9]。通过Patran对柔性体的有限元网格划分,然后采用Nastran求解得到柔性体中性文件MNF,导入ADAMS后建立扭转梁刚柔耦合模型。扭梁柔性体与纵臂的连接为固定铰链。图 2是衬套安装角度的定义。

|
图 1 扭转梁悬架模型 |
|
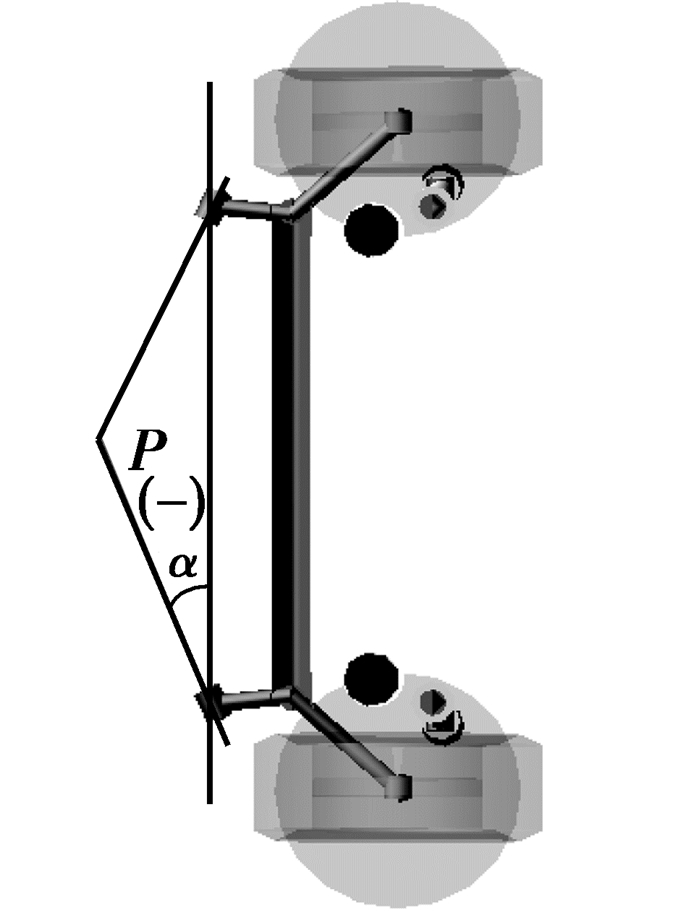
图 2 衬套安装角度 |
纵臂与车身是橡胶衬套连接(见图 2)。橡胶衬套的安装角度定义为衬套的中心轴线与垂直线的夹角,规定顺时针为正,逆时针为负。衬套的初始安装角度是-25°。通过定义衬套安装轴线的硬点坐标的参数化可以实现衬套安装角度的改变。将在Isight软件DOE[10]模块中利用参数化的硬点坐标分析衬套安装角度对悬架K & C及整车操稳的敏感性。
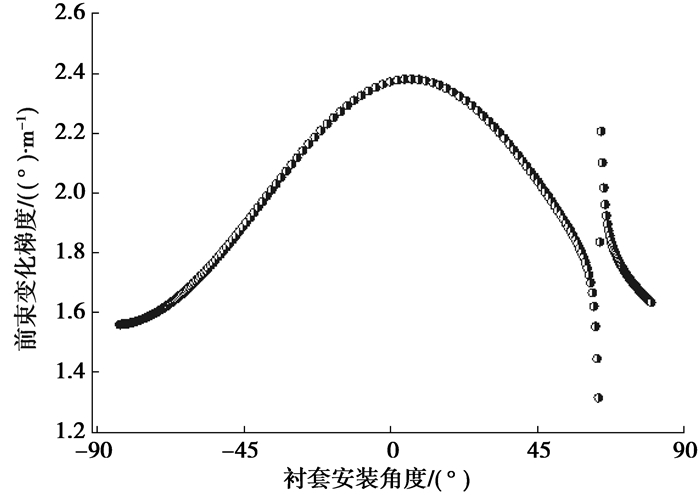
车辆转弯时,外侧车轮相对于车身上跳,内侧车轮相对于车身下跳,悬架产生反向跳动。为了保证车辆的不足转向特性,后轮前束角应增大。图 3为反向跳动时前束变化梯度与衬套安装角度的关系。可以看出,衬套安装角度在8°的时候前束变化梯度最大。还能看出,扭转梁悬架衬套安装角度在整个范围内变化,前束变化梯度都不大。另外,在衬套安装角度为63.5°左右时,前束变化会比较敏感。前束变化梯度增大有利于车辆的不足转向,但也不能太大,否则会引起轮胎的磨损。
|
图 3 前束角与衬套角度关系 |
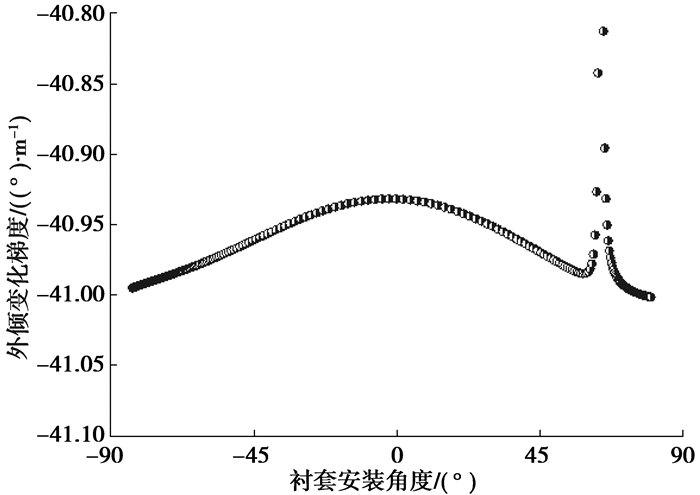
图 4所示为反向跳动时外倾变化梯度与衬套安装角度的关系。可以看出,衬套安装角度在0°的时候外倾变化梯度绝对值最小,这不利于车辆的不足转向特性,在不导致轮胎磨损的情况下,一般希望负外倾大一点。同样,在衬套安装角度为63.5°左右时,外倾变化非常敏感,会产生突变。
|
图 4 外倾角与衬套角度关系 |
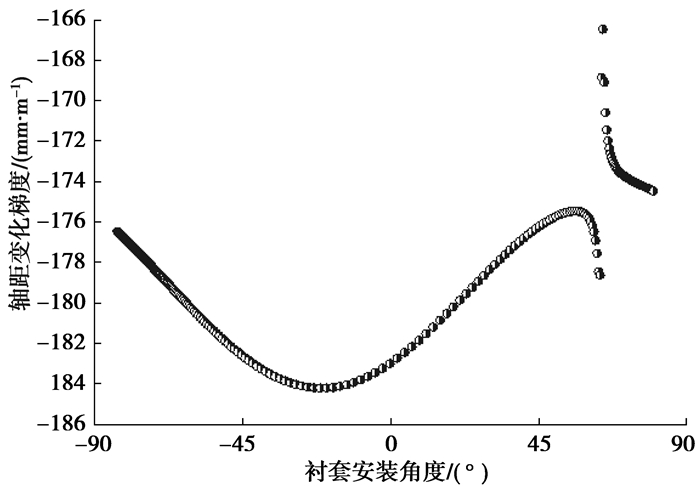
图 5为同向跳动时轴距变化梯度与衬套安装角度的关系。从提高车辆的平顺性考虑,后轮通过凸块时,轴距应该增大,也就是轴距变化梯度为正,以提高悬架的退让性。从图 5可以看出,轴距变化为负,也就是轴距减小,衬套安装角度在5.6°的时候轴距负向变化梯度最大。因此该扭转梁悬架不利于后轮的平顺性,尤其衬套安装角度为图中曲线最低拐点值5.6°时。

|
图 5 轴距与衬套角度关系 |
图 6所示为反向跳动时轮距变化梯度与衬套安装角度的关系。从图中看出,衬套安装角度为-22°时,轮距变化梯度最大。一般希望在正常工作范围下,轮距变化尽量小,因此衬套的这个安装角度这对轮胎的磨损不利。
|
图 6 轮距与衬套角度关系 |
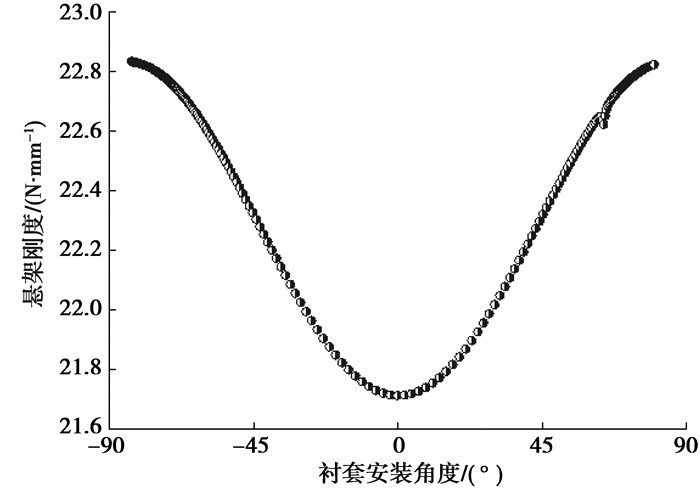
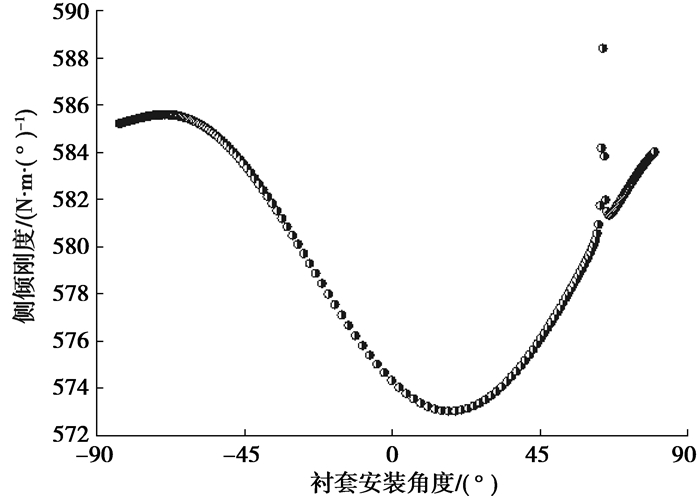
图 7、图 8为悬架刚度和侧倾角刚度与衬套安装角度的关系。从图中可看出,衬套安装角度在0°时,悬架刚度最小。衬套安装角度在15°左右时,悬架的侧倾角刚度最小。悬架的刚度小有利于乘员的乘坐舒适性,但应满足偏频设计的要求。后悬架的侧倾刚度小一点能减少后轮的载荷转移,提高车辆的不足转向特性,但同时应满足悬架设计对前后悬架侧倾角刚度匹配的要求。
|
图 7 悬架刚度与衬套角度关系 |
|
图 8 侧倾刚度与衬套角度关系 |
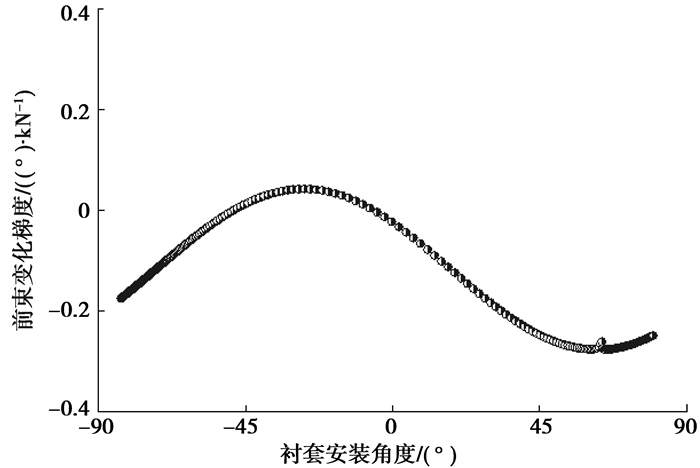
为了保证后轴的稳定性,增加不足转向,后悬在受到侧向力作用时,前束角的变化方向应与侧向力作用方向一致,这就是随动转向,因此前束变化梯度应为正。从图 9可以看出,衬套安装角度在-49°~-7°范围时,前束变化梯度为正;在衬套安装角度为-26°左右时,后轴的随动转向最明显;在其他的衬套安装角度范围时不满足随动转向的要求。
|
图 9 前束角与衬套角度关系 |
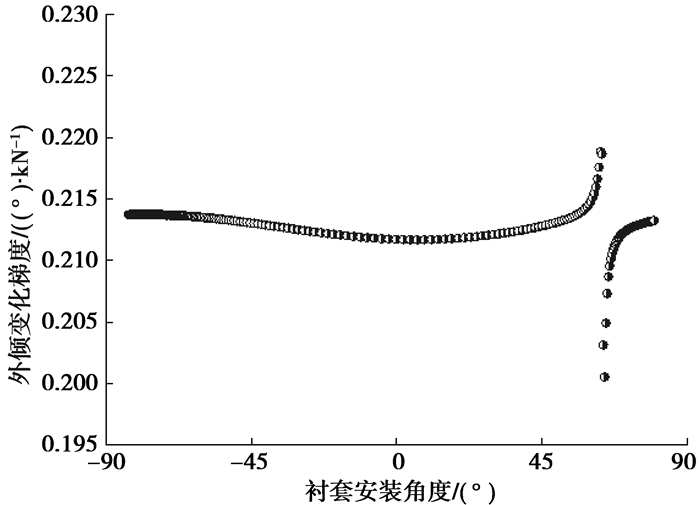
图 10所示为外倾变化梯度与衬套安装角度的关系。在侧向力作用时,外倾角应正向变化,因此外倾变化梯度须为正值。外倾梯度大一点有利于提高车轮的抓地力和附着性。
|
图 10 外倾角与衬套角度关系 |
扭转梁悬架对后轴稳定性的影响主要是由于侧向力作用下纵臂与车身连接衬套变形引起的。这个衬套的变形分为2个部分。
Ⅰ:衬套的轴向变形,衬套轴向变形产生的轴向移动使得后轴产生不足转向。轴向刚度越低,不足转向越明显。
Ⅱ:衬套的径向变形,衬套径向变形产生的轴向移动使得后轴产生过多转向。径向刚度越低,过多转向越明显。
2.3 悬架K & C分析总结表 1为衬套安装角度对K & C特性影响的总结。
| 表 1 衬套安装角度总结 |
从前边的分析看出,悬架的K & C与衬套安装角度的关系很复杂。悬架的多个K & C特性之间是耦合的关系。不存在一个衬套安装角度使得所有的K & C性能都最好,而实际上各性能之间往往存在矛盾,在某个性能变好的同时会使其他性能变差,因此要在性能之间取舍达到一个折中的方案[11]。
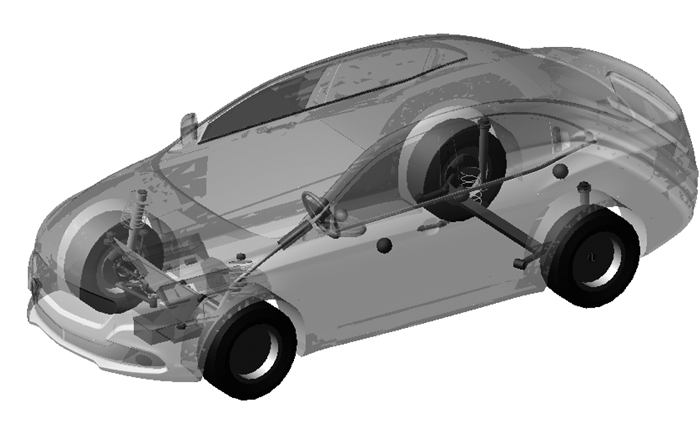
3 操纵稳定性影响分析 3.1 稳态操稳分析 3.1.1 整车仿真模型如图 11所示,整车模型前悬架为一麦弗逊悬架,后悬架为文中研究的扭转梁式悬架,整车的建模参数如表 2所示。轮胎使用MF-TYRE轮胎。
|
图 11 整车模型 |
| 表 2 整车参数 |
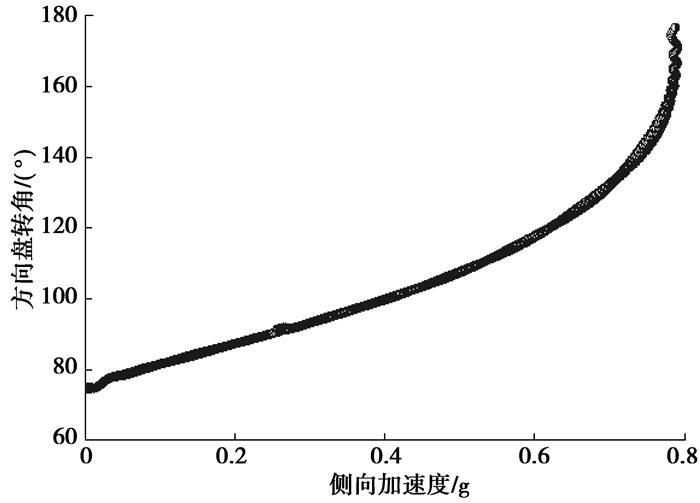
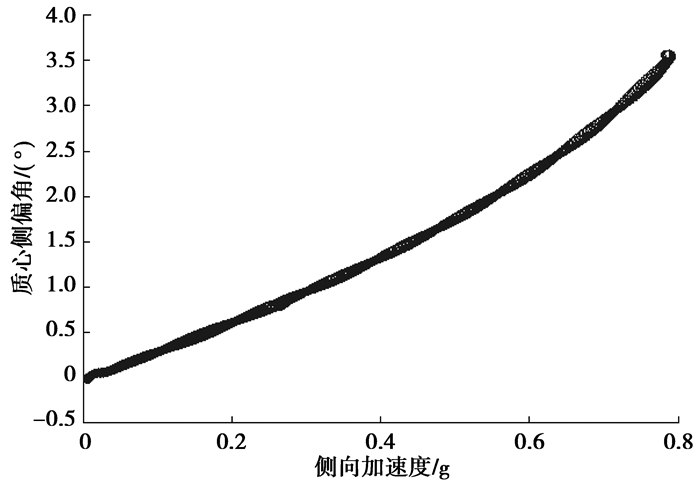
稳态分析工况为定半径稳态回转,半径为40 m,最高车速为65 km/h。图 12为方向盘转角SWA与侧向加速度关系曲线,图 13为质心侧偏角与侧向加速度关系曲线。
|
图 12 方向盘转角_侧向加速度 |
|
图 13 质心侧偏角_侧向加速度 |
最大侧向加速度,0.7 g侧向加速度方向盘转角可由图 11求得。稳态不足转向度为在0.4 g侧向加速度时,方向盘转角对侧向加速度曲线的斜率。0.7 g侧向加速度时质心侧偏角可由质心侧偏角对侧向加速度曲线求得。
表 3是初始衬套安装角度-25°时,整车的定半径稳态回转性能指标。
| 表 3 稳态性能指标 |
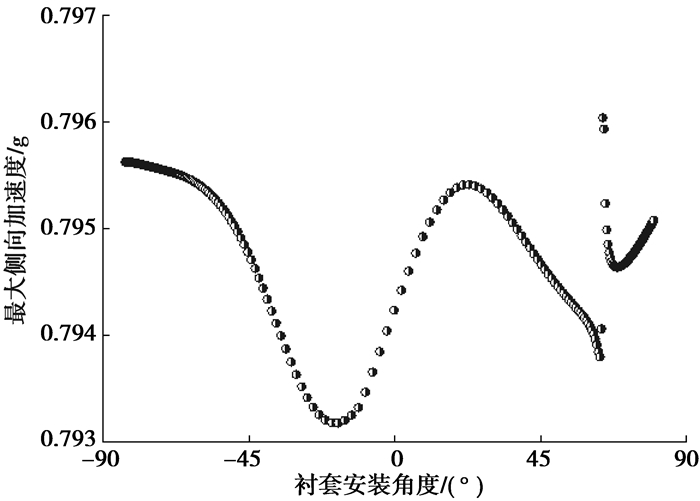
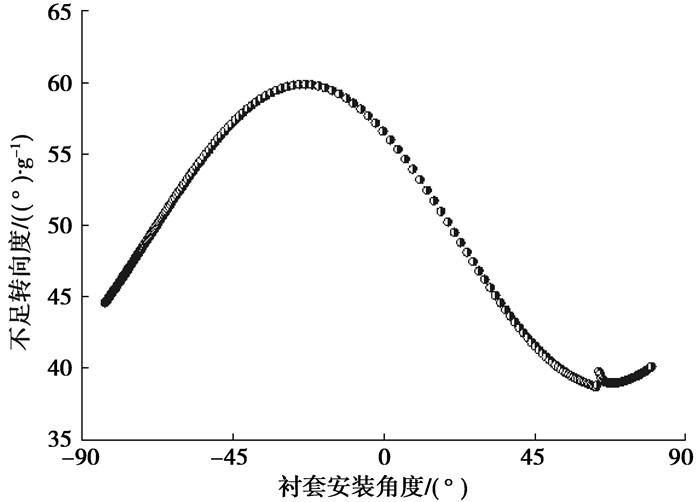
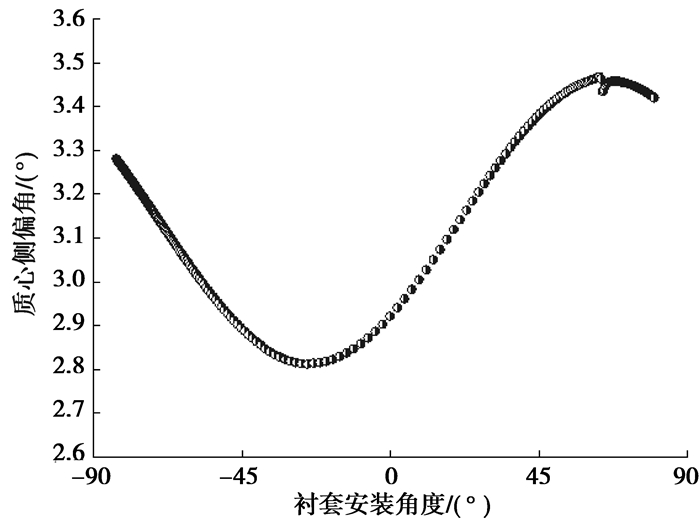
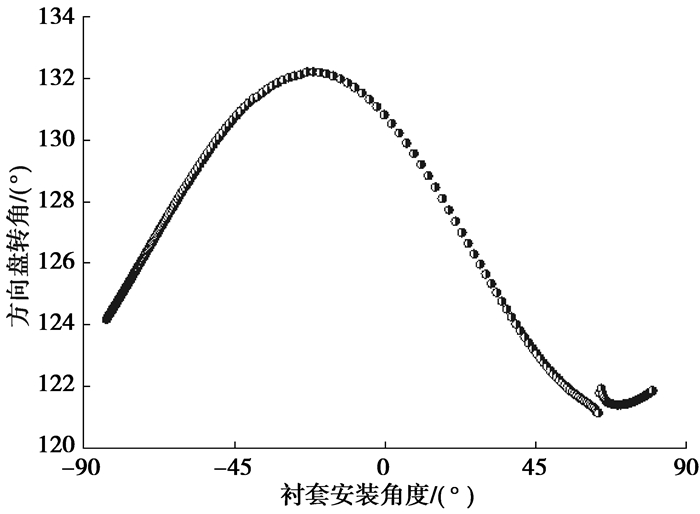
图 14~图 17分别是最大侧向加速度、不足转向度、质心侧偏角、方向盘转角与衬套安装角度关系。可以看出,衬套安装角度在-25.5°左右时,稳态回转的不足转向度最大,质心侧偏角最小,0.7 g侧向加速度对应的方向盘转角最大,也就是车辆的不足转向特性最好。对比前边悬架侧向力工况的分析,在衬套安装角度为-25.5°左右时,前束变化梯度最大,可知稳态工况下车辆的后轴的不足转向性能主要受后轴的随动转向性能影响。从图 13看出,最大侧向加速度在衬套安装角度为63.5°左右时很敏感,这与前边对悬架K & C的分析吻合。
|
图 14 对最大侧向加速度影响 |
|
图 15 对不足转向度影响 |
|
图 16 对质心侧偏角影响 |
|
图 17 对方向盘转角影响 |
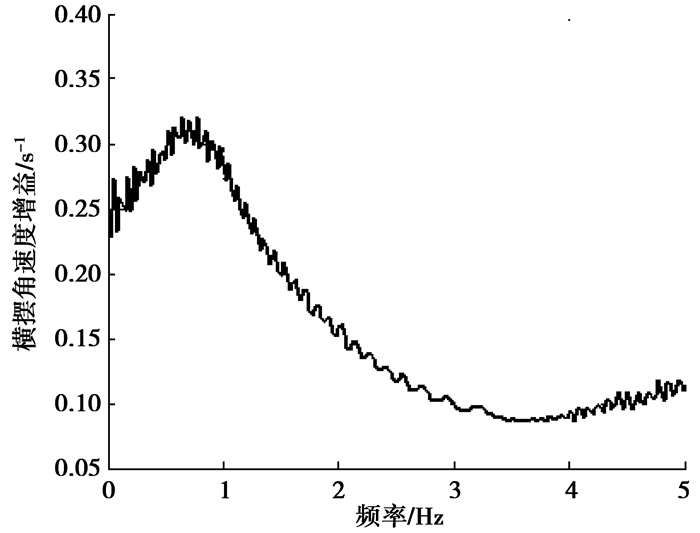
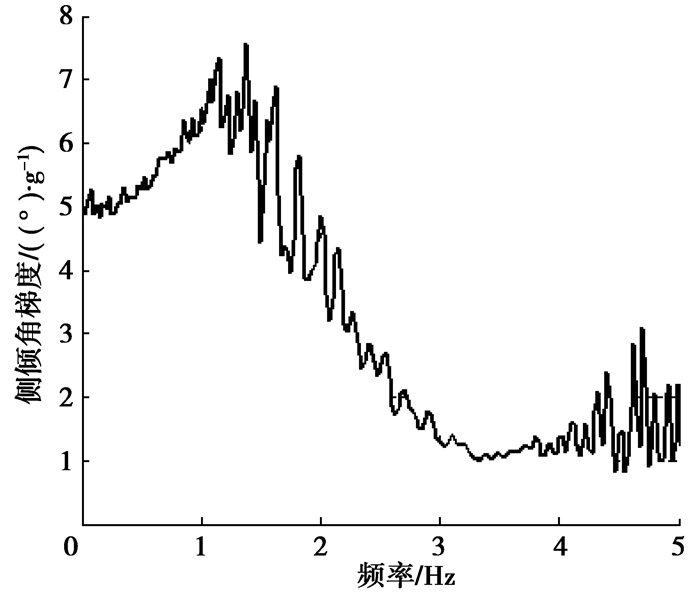
瞬态分析为方向盘扫频输入,方向盘输入的最大转角为25°。图 18~图 21为在初始衬套安装角度-25°时,瞬态横摆角速度增益、侧倾角增益、侧向加速度_方向盘转角延迟时间(用DT1表示)、侧向加速度_横摆角速度延迟时间(用DT2表示)与方向盘转角输入频率关系。
|
图 18 横摆角速度增益 |
|
图 19 侧倾角了增益 |
|
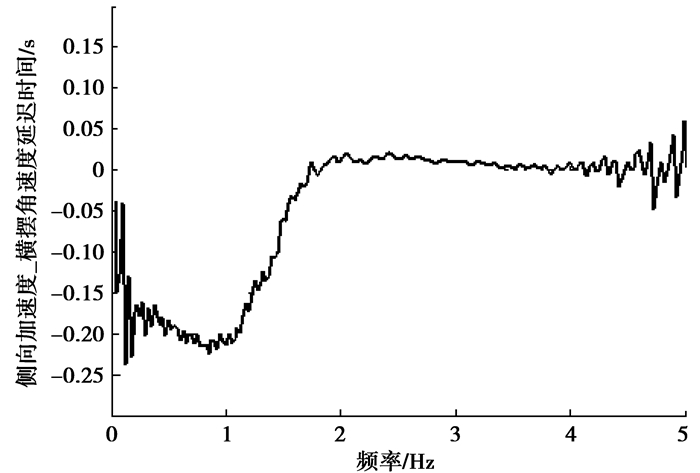
图 20 DT1延迟 |
|
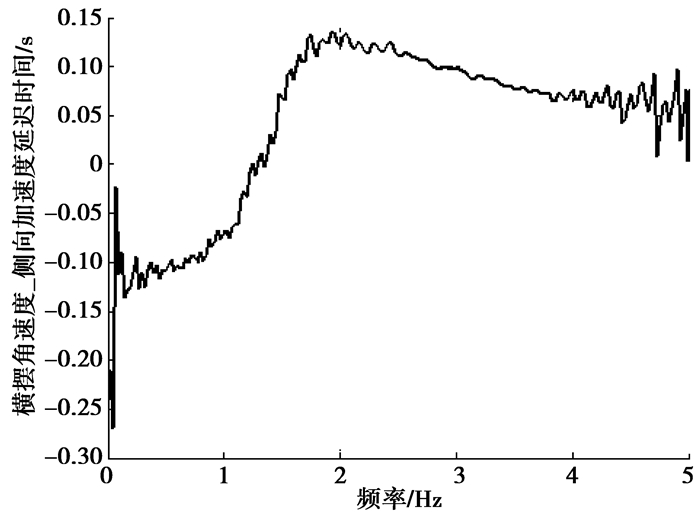
图 21 DT2延迟 |
文中将研究衬套安装角度对上述参数在方向盘转角输入频率为0.5 Hz时值的影响。表 4是初始状态下的瞬态性能指标。横摆角速度共振频率为图 18中最大横摆角速度增益对应的频率。
| 表 4 瞬态性能指标 |
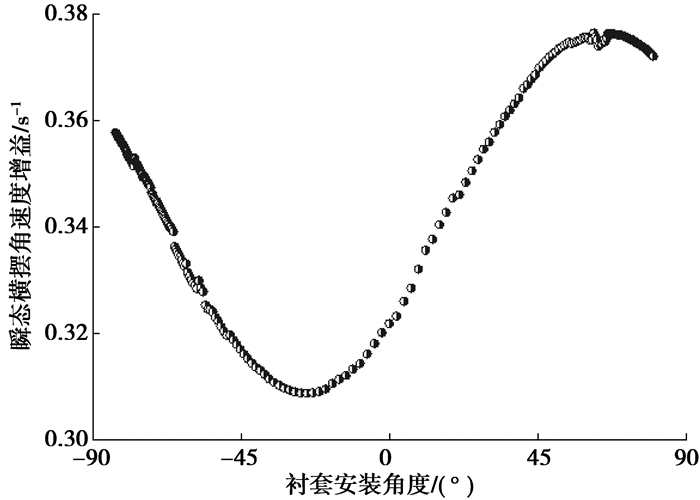
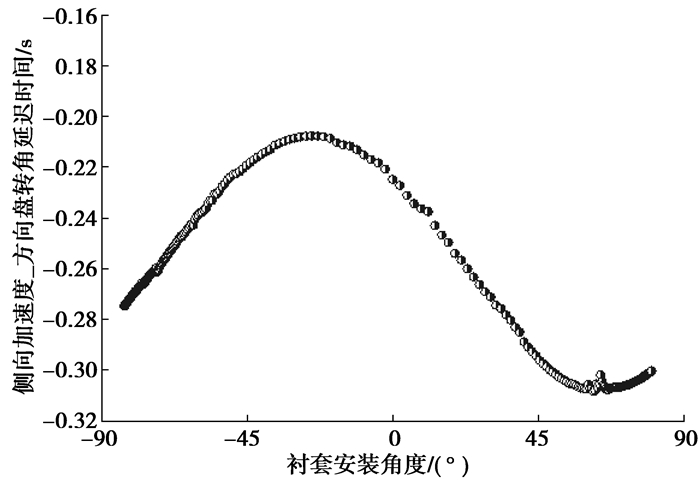
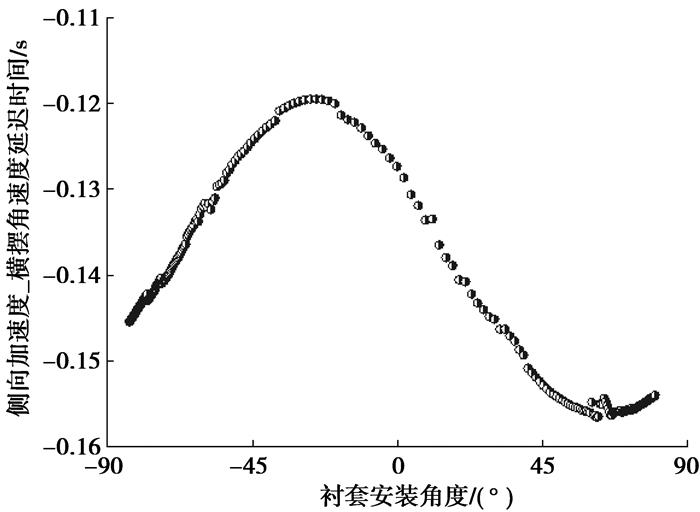
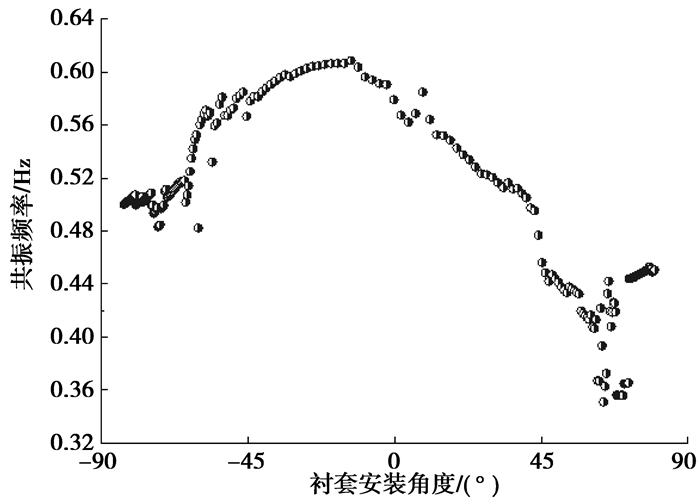
图 22~图 25分别是瞬态横摆角速度增益、侧向加速度_方向盘转角延迟时间、横摆角速度_侧向加速度延迟时间、共振频率与衬套安装角度的关系。可以看出,衬套安装角度在-25.5°左右时,瞬态横摆角速度增益最小、侧向加速度_方向盘转角延迟时间最小、横摆角速度_侧向加速度延迟时间最小、共振频率最大。对比前边悬架侧向力工况的分析,在衬套安装角度为-25.5°左右时,前束变化梯度最大,可知瞬态工况下车辆后轴的稳定性能主要受后轴随动转向性能影响。
|
图 22 对横摆角速度增益影响 |
|
图 23 对DT1影响 |
|
图 24 对DT2影响 |
|
图 25 对共振频率影响 |
从前面衬套安装角度与车辆的操稳性能指标关系的分析看出,整车的操稳特性与衬套安装角度并不是简的、线性的、一对一的关系。而是复杂的耦合关系,并不存在一个衬套安装角度使得车辆的所有操稳指标都达到最优。实际车辆也往往更侧重于某几方面的性能,要在各指标间取得一个权衡,因此对操稳性能的多目标协同优化首先要对各个目标进行归一化处理,然后分配一个权重系数[12]。各目标的优化方向及权重系数见表 5所示。
| 表 5 优化方向(约束条件-90°<α<90°) |
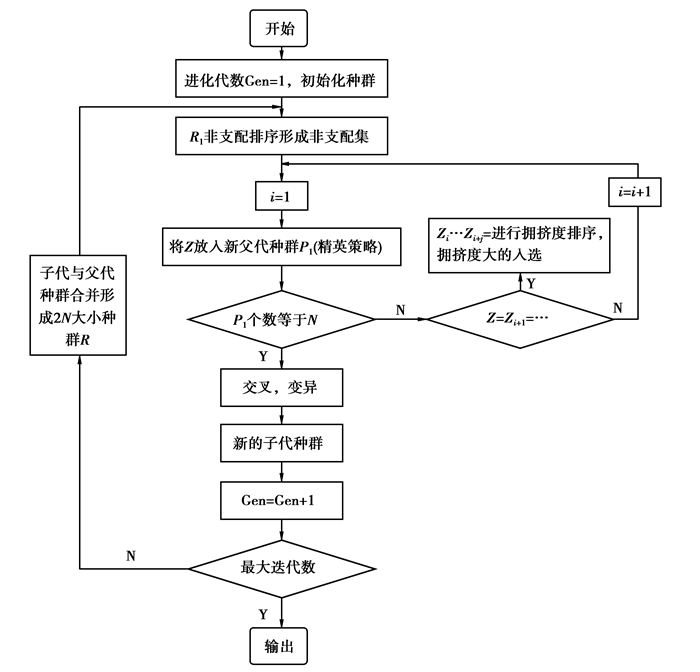
为了优化整车的操稳性能,优化采用NSGA-Ⅱ多目标优化算法。NSGA-Ⅱ[13-14]是遗传算法改进的多目标优化算法。图 26为NSGA-Ⅱ算法,首先从群体中选出非劣解集,并将层级设置为1,从余下的群体中选出非劣解集,并将层级设置为2,依此循环计算。NSGA-Ⅱ算法通过拥挤距离来度量非劣解集的距离,使解集在空间中均匀分布、不过于集中。同时,采用精英策略,加速算法的收敛,如图 26所示。经过计算最后得到的解为Pareto解[14-16],也称Pareto前沿,然后可在Pareto解中根据实际需要选择一个最优解。
|
图 26 NSGA-Ⅱ优化算法 |
优化目标是定半径稳态回转和方向盘扫频输入的操稳性能指标:最大侧向加速度,不足转向度、0.7 g侧向加速度时质心侧偏角和方向盘转角,以及瞬态横摆角速度增益、横摆角速度共振频率、侧向加速度_方向盘转角延迟时间、侧向加速度_横摆角速度延迟时间。文中NSGA-Ⅱ计算选取种群数量10,遗传代数20,交叉率0.9。表 5是各指标的优化方向。
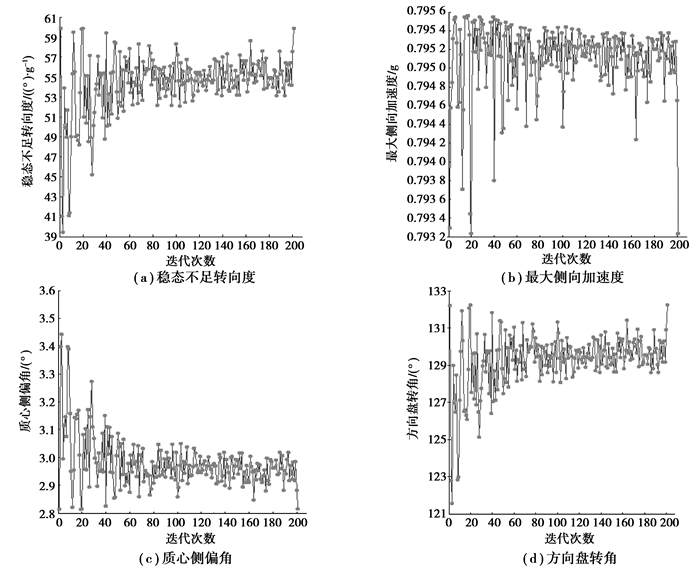
4.3 优化结果图 27为稳态不足转向度、最大侧向加速度、0.7 g侧向加速度时质心侧偏角、0.7 g侧向加速度时方向盘转角的优化迭代过程曲线。可以看出,不足转向度、最大侧向加速度、方向盘转角向增大的方向收敛,质心侧偏角向减小的方向收敛。这与优化方向一致。
|
图 27 稳态指标优化迭代曲线 |
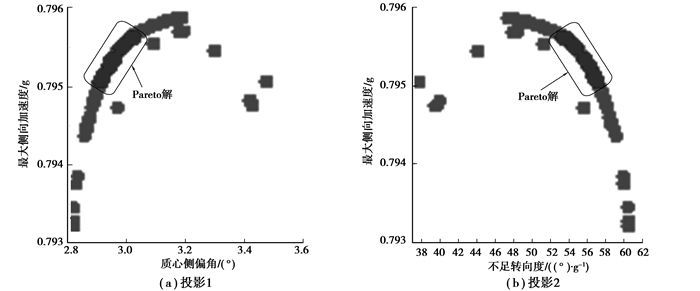
图 28(a)、(b)分别为Pareto解【在侧向加速度_质心侧偏角】平面投影1和【侧向加速度_不足转向度】平面投影2。
|
图 28 Pareto解在稳态指标平面上的投影 |
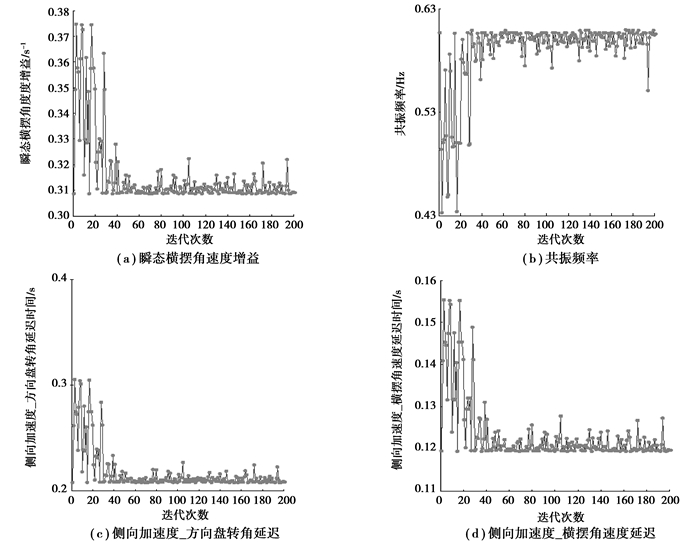
图 29为横摆角速度增益、横摆角速度共振频率、侧向加速度_方向盘转角延迟时间、侧向加速度_横摆角速度延迟时间的优化迭代过程曲线。可以看出,横摆角速度增益、侧向加速度_方向盘转角延迟时间、侧向加速度_横摆角速度延迟时间向减小的方向收敛,横摆角速度共振频率向增大的方向收敛。与前边定义的优化方向一致。
|
图 29 瞬态指标优化迭代曲线 |
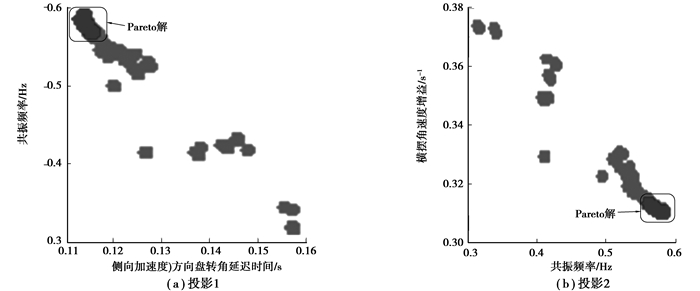
图 30(a)、(b)分别为Pareto解在【共振频率_侧向加速度对方向盘转角延迟时间】平面投影1和【横摆角速度增益_共振频率】平面投影2。
|
图 30 Pareto解在瞬态指标平面上的投影 |
表 6为经过优化前后的操稳性能指标对比,可以看出,整车的主要操稳性能都得到了提升。
| 表 6 优化结果对比 |
从前面分析看出,通过调整衬套的安装角度能够改善车辆的不足转向特性,具体衬套的安装角度的确定应根据衬套的轴向、径向刚度来定。衬套安装角度过大,会使得侧向力沿衬套的轴向分量减小,轴向变形小,衬套安装角度过小,不能把衬套的轴线变形转化为扭梁的转向特性,都会减小不足转向趋势。
5 结论在建立扭转梁悬架刚柔耦合模型的基础上,详细分析了纵臂与车身连接处衬套安装角度对悬架K & C的影响。求解了K & C特性指标与衬套安装角度的非线性关系曲线,并计算出对前束角、轴距、侧倾刚度等悬架参数最敏感的衬套安装角度。通过对非线性曲线的分析表明不存在一个衬套安装角度使得所有的K & C性能都最好,各性能之间往往存在矛盾,要在性能之间取得一个平衡。
在悬架K & C分析的基础上,进一步研究了衬套安装角度对操纵稳定性指标的影响。通过计算,得出了衬套安装角度与稳态和瞬态操纵稳定性指标的非线性关系曲线,通过与K & C分析曲线的对比。表明操稳性能和悬架的K特性和C特性有直接的关系,尤其随动转向特性,也就是侧向力作用下的前束角变化对操纵稳定性的影响最显著。可以通过优化衬套安装角度来改变悬架的K & C特性,从而改善整车的操稳性能。
基于NSGA-Ⅱ多目标优化算法,确定操纵稳定性能指标的优化方向和衬套安装角度的范围,对操纵稳定性能指标进行多目标协同优化得到Pareto解和安装角度的优化解,使车辆的各方面操稳性能都得到了提升。
| [1] |
刘艳华.
轿车扭力梁后悬架的研究与开发[J]. 沈阳大学学报, 2006, 18(4): 5–8.
LIU Yanhua. Development and research of twist beam rear suspension[J]. Journal of Shenyang university, 2006, 18(4): 5–8. (in Chinese) |
| [2] | Sista P, Kang H T. Twist beam suspension design and analysis for vehicle handling and rollover behavior[J]. SAE Technical Paper, 2010: 1–10. |
| [3] | Leal V, Landre J, Bitencourt R.Twist beam rear suspension-influences of the cross section member geometry in the elastokinematics behavior[J].SAE Technical Paper, 2007-01-2860, 2007, doi:10.4271/2007-01-2860. |
| [4] | Janarthanam B, Ghodekar S, Apte A.Virtual development of optimum twist beam design configuration for a new generation passenger car[J].SAE Technical Paper, 2007-01-3562, 2007, dio:10.4271/2007-01-3562. |
| [5] |
江浩斌, 李超, 徐兴, 等.
扭转梁式后悬架结构参数对侧倾振动影响[J]. 重庆交通大学学报:自然科学版, 2012, 31(5): 1066–1070.
JIANG Haobin, LI Chao, XU Xing, et al. Research on the structure parameters of twist beam rear suspension on the roll vibration characteristics[J]. Journal of Chongqing Jiaotong University:Natural Science, 2012, 31(5): 1066–1070. (in Chinese) |
| [6] |
虞健, 左曙光, 陈栋华, 等.
扭转梁半独立悬架建模与动态特性分析[J]. 系统仿真学报, 2006, 18(8): 2300–2306.
YU Jian, ZUO Shuguang, CHEN Donghua, et al. Modeling and dynamic character analyzing of twist beam rear suspension on ADAMS[J]. Journal of System Simulation, 2006, 18(8): 2300–2306. (in Chinese) |
| [7] |
景立新, 郭孔辉.
扭转梁式后悬架运动学和动力学分析[J]. 吉林大学学报:工学版, 2010, 40(S): 1–5.
JING Lixin, GUO Konghui. Kinematics and compliance characteristics of twist beam rear suspension[J]. Journal of JinLin University:Engineering and Technology Edition, 2010, 40(S): 1–5. (in Chinese) |
| [8] |
梅声远, 张维刚, 赵国峰, 等.
扭转梁半独立后悬架结构强度及动态特性有限元分析[J]. 汽车工程, 2012, 34(11): 990–994.
MEI Shengyuan, ZHANG Weigang, ZHAO Guofeng, et al. Finite element analysis on the structure strength and dynamic characteristics of torsion beam semi-independent rear suspension[J]. Automotive Engineering, 2012, 34(11): 990–994. DOI:10.3969/j.issn.1000-680X.2012.11.006 (in Chinese) |
| [9] |
李杰, 张喆, 朱毅杰, 等.
平衡悬架钢板弹簧模型的建立与仿真[J]. 重庆大学学报, 2011, 34(6): 31–35.
LI JIE, ZHANG ZHE, ZHU YI-JIE, et al. Modeling and Simulation of leaf spring for tandem suspension[J]. Journal of Chongqing university, 2011, 34(6): 31–35. DOI:10.11835/j.issn.1674-4764.2011.06.007 (in Chinese) |
| [10] | Spelta C, Savaresi S M. Experimental analysis of a motorcycle semi-active rear suspension[J]. Control Engineering Practice, 2010, 18(11): 1239–1250. DOI:10.1016/j.conengprac.2010.02.006 |
| [11] |
郭孔辉, 吴利广, 金凌鸽, 等.
悬架衬套安装方向优化设计[J]. 汽车技术, 2010(4): 1–7.
GUO Konghui, WU Liguang, JIN Lingge, et al. The optimization of suspension bushing mounting direction[J]. Automotive Technology, 2010(4): 1–7. (in Chinese) |
| [12] |
奉铜明, 钟志华, 闫晓雷, 等.
基于NSGA-Ⅱ的多连杆悬架多目标优化[J]. 汽车工程, 2010, 32(12): 1063–1066.
FENG Tongming, ZHONG Zhihua, YAN Xiaolei, et al. Muti-objective optimization for muti-link suspension based on NSGA-Ⅱ algorithm[J]. Automotive Engineering, 2010, 32(12): 1063–1066. (in Chinese) |
| [13] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transaction on Evolutionary Computation, 2002, 6(2): 182–197. DOI:10.1109/4235.996017 |
| [14] |
李伟平, 王世东, 周兵, 等.
基于响应面法和NSGA-Ⅱ算法的麦弗逊悬架优化[J]. 湖南大学学报:自然科学版, 2011, 38(6): 27–32.
LI Weiping, WANG Shidong, ZHOU Bing, et al. Macpherson suspension parameter optimization based on response surface method and NSGA-Ⅱalgorithm[J]. Journal of Hunan University:Natural Science, 2011, 38(6): 27–32. (in Chinese) |
| [15] | 金陵鸽. C级车悬架KnC特性优化设计方法研究[D]. 长春: 吉林大学博士学位论文, 2010: 94-113. http://cdmd.cnki.com.cn/Article/CDMD-10183-2011014334.htm |
| [16] | Konak A, Coit D W, Smith A E. Muti-objective optimization using genetic algorithms, a tutorial[J]. Reliability Engineering and System Safety, 2006, 91: 992–1007. DOI:10.1016/j.ress.2005.11.018 |
| [17] |
王涛.
汽车悬架参数的多目标多决策优化[J]. 农业机械学报, 2009, 40(4): 27–32.
WANG Tao. Muti-objective and muti-criteria decision optimization of automobile suspension parameters[J]. Transaction of the Chinese Society for Agricultural machinery, 2009, 40(4): 27–32. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

