2. 中南大学, 土木工程学院, 长沙 410075;
3. 重庆大学, 资源及环境科学学院, 重庆 400044
2. School of Civil Engineering, Central South University, Changsha 410075, China;
3. School of Resource and Environment Science, Chongqing University, Chongqing 400044, China
边坡稳定性问题,一直是岩土工程界的热门研究主题。安全系数和可靠度是评价边坡稳定性的2个重要指标。由于安全系数没有考虑参数随机性和离散性对结果的影响,导致实际工程中很多结构在满足安全系数的条件下依然出现了破坏现象[1-2]。由此,使得应用可靠性理论和推行概率方法进行结构安全性评价,成为当今国内外结构评价发展的必然趋势。
边坡结构可靠度计算的误差主要来源于模型的建立、参数的推断和算法的选取3个方面。在模型建立方面,目前应用最广泛的是极限平衡法,该方法理论简单,易于实施,但所作假设比较多,求解过程繁琐。根据塑性理论可知该法所获得的解,既不是严格的上限解,也不是严格的下限解。另一个广泛应用的方法是有限元法[3-4],可以分析任意土质、几何、荷载、边界和本构条件,但其所得到的极限荷载值可能高于或者可能低于真实的极限荷载,给工程带来隐患。而应用极限分析法可以得到边坡极限荷载的严格上限解[5-11],在此基础上应用上限理论建立可靠度计算模型,可获得严格可靠度上限值,这对于评价边坡的稳定性具有重要的参考价值。在参数推断方面,一般是先假设随机变量服从某种分布,然后通过检验确定是否接受假设,或者通过经验确定分布特征,这些做法由于添加了主观因素而偏离了事实。目前,最适用的是采用最大熵原理进行推断,该方法不添加任何主观因素,能估计出最接近样本真实分布统计特征[12-16]。在可靠度算法选取方面,现主要有矩法[17]、最优化法、响应面法[18]、随机有限元法、、Monte Carlo模拟法5类。目前在所有的可靠度计算方法中,只有Monte Carlo模拟法被认为是一种相对精确的方法[19-21],根据大数定律,只要抽样次数足够大,其精度就能足够高。当抽样次数达到100万次可基本认为是相对精确解。
综合运用极限分析方法、最大熵理论和Monte Carlo模拟法所计算的边坡结构可靠度值是一个严格的可靠度上限,比传统方法所获得的值更加准确、可靠。
1 基于上限定理的边坡稳定可靠性模型以图 1所示的具有坡顶倾角α和坡角β的边坡进行分析,考虑通过坡趾下方的对数螺旋线旋转间断机构为假想破坏机构[22]。ABC′A区绕旋转中心O相对BC以下作刚体旋转,速度为V。为便于分析问题,选线OB和OC倾角分别为θ0和θh,线AC′与水平线夹角为β′,高度为H,OB的长度为r0,AB的长度为L,CC′的长度为D。其中,角度变量θ0, θh和β′完全由假想机构给定。
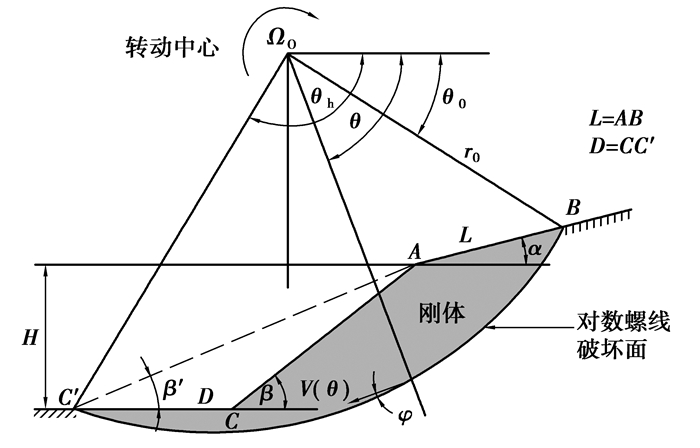
|
图 1 破坏面通过坡趾下方的边坡破坏机构 |
首先分别求出OBC′O, OABO, OAC′O和ACC′A区由土的重力所做的功率W1,W2,W3和W4,则可得到ABC′CA区的外功率W0=W1-W2-W3-W4。经代数运算后,可得到ABC′CA区由土的重力所做的总外功率为
| $ {W_0} = \gamma \mathit{\Omega r}_0^3\left( {{f_1} - {f_2} - {f_3} - {f_4}} \right), $ | (1) |
式中,γ是土的容重;Ω是ABC′CA区的角速度;函数f1(θh, θ0),f2(θh, θ0),f3(θh, θ0)和f4(θh, θ0, β′)的表达式为
| $ {f_1}\left( {{\theta _h},{\theta _0}} \right) = \frac{1}{{3\left( {1 + 9{{\tan }^2}\varphi } \right)}}\left\{ {\left( {3\tan \varphi \cos {\theta _h} + \sin {\theta _h}} \right)\exp \left[ {3\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi } \right] - \\ \left( {3\tan \varphi \cos {\theta _0} + \sin {\theta _0}} \right)} \right\}, $ | (2) |
| $ {f_2}\left( {{\theta _h},{\theta _0}} \right) = \frac{L}{{6{r_0}}}\left( {2\cos {\theta _0} - \frac{L}{{{r_0}}}\cos \alpha } \right)\sin \left( {{\theta _0} + \alpha } \right), $ | (3) |
| $ \begin{array}{*{20}{c}} {{f_3}\left( {{\theta _h},{\theta _0}} \right) = \frac{1}{6}\exp \left[ {\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi } \right]\left[ {\sin \left( {{\theta _h} - {\theta _0}} \right) - \frac{L}{{{r_0}}}\sin \left( {{\theta _h} + \alpha } \right)} \right]}\\ {\left\{ {\cos {\theta _0} - \frac{L}{{{r_0}}}\cos \alpha + \cos {\theta _h}\exp \left[ {\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi } \right]} \right\},} \end{array} $ | (4) |
| $ {f_4}\left( {{\theta _h},{\theta _0},\beta '} \right) = {\left( {\frac{H}{{{r_0}}}} \right)^2}\frac{{\sin \left( {\beta - \beta '} \right)}}{{2\sin \beta \sin \beta '}}\left[ {\cos {\theta _0} - \frac{{L\cos \alpha }}{{{r_0}}} - \frac{H}{{3{r_0}}}\left( {\cot \beta ' + \cot \beta } \right)} \right]。$ | (5) |
从几何关系可以得出比值H/r0和L/r0,分别为
| $ \frac{H}{{{r_0}}} = \frac{{\sin \beta }}{{\sin \left( {\beta - \alpha } \right)}}\left\{ {\sin \left( {{\theta _h} + \alpha } \right)\exp \left[ {\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi } \right] - \sin \left( {{\theta _0} + \alpha } \right)} \right\}, $ | (6) |
| $ \frac{L}{{{r_0}}} = \frac{{\sin \left( {{\theta _h} - {\theta _0}} \right)}}{{\sin \left( {{\theta _h} + \alpha } \right)}} - \frac{{\sin \left( {{\theta _h} + \beta } \right)}}{{\sin \left( {{\theta _h} + \alpha } \right)\sin \left( {\beta - \alpha } \right)}}\left\{ {\exp \left[ {\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi } \right]\sin \left( {{\theta _h} + \alpha } \right) - \sin \left( {{\theta _0} + \alpha } \right)} \right\}。$ | (7) |
1) 内部耗损率
对整个间断面BC′积分可得到总的内部能量耗损率为
| $ \int {{\theta _{{h_{{\theta _0}}}}}c\left( {V\cos \varphi } \right)\frac{{r{\rm{d}}\theta }}{{\cos \varphi }}} = \frac{{cr_o^2\mathit{\Omega }}}{{2\tan \varphi }}\left\{ {\exp \left[ {2\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi } \right] - 1} \right\}。$ | (8) |
2) 约束函数
使式(1)的外功率与式(8)的内部能量耗损率相等,得约束函数:
| $ F\left( {c,\gamma } \right) = c \cdot f\left( {{\theta _h},{\theta _0},\beta '} \right) - H\gamma = 0。$ | (9) |
式中f(θh, θ0, β′)的定义为
| $ f\left( {{\theta _h},{\theta _0},\beta '} \right) = \frac{{\sin \beta '\left\{ {\exp \left[ {2\left( {{\theta _h} - {\theta _0}} \right)\tan \varphi } \right] - 1} \right\}}}{{2\sin \left( {\beta ' - \alpha } \right)\tan \varphi \left( {{f_1} - {f_2} - {f_3} - {f_4}} \right)}}\left\{ {\sin \left( {{\theta _h} + \alpha } \right)\exp \left[ {\left( {{\theta _h} -\\ {\theta _0}} \right)\tan \varphi } \right] - \sin \left( {{\theta _0} + \alpha } \right)} \right\}。$ | (10) |
当θh,θ0和β′(β′≤β)满足条件
| $ \frac{{\partial f}}{{\partial {\theta _h}}} = 0,\frac{{\partial f}}{{\partial {\theta _0}}} = 0,\frac{{\partial f}}{{\partial \beta '}} = 0, $ | (11) |
时,函数f(θh, θ0, β′)有1个最小值minf(θh, θ0, β′)。
如果以函数
| $ F\left( {c,\gamma } \right) = c \cdot \min f\left( {{\theta _h},{\theta _0},\beta '} \right) - H\gamma = 0, $ | (12) |
为约束函数求得的可靠度则为边坡的最小可靠度上限值,式中c, γ为随机变量。
2 基于最大熵原理的统计特征推断 2.1 信息熵设X是取有限个值的随机变量
| $ {p_i} = \left\{ {X = {x_i}} \right\},i = 1,2, \cdots ,n, $ | (13) |
即X取xi的先验概率为pi。
则X的熵定义为
| $ H\left( X \right)=H\left( {{p}_{1}},{{p}_{2}},\cdots ,{{p}_{n}} \right)=-k\sum\limits_{i=1}^{\mathit{n}}{\left( {{p}_{i}}\cdot {{\log }_{a}}{{p}_{i}} \right)}, $ | (14) |
H(X)称为信息熵。为了方便运算,取k=1,取自然对数e为底,则式(14)可表示为
| $ H\left( X \right) = H\left( {{p_1},{p_2}, \cdots ,{p_n}} \right) = - \sum\limits_{i = 1}^n {\left( {{p_i} \cdot \ln {p_i}} \right)} 。$ | (15) |
如果随机变量X为连续分布,其分布密度函数为p(x),则定义X的熵为
| $ H\left( x \right) = - \int_R {p\left( x \right)\ln p\left( x \right){{\rm{d}}_x}} 。$ | (16) |
最佳密度函数为
| $ \max H\left( x \right) = - \int_R {p\left( x \right)\ln p\left( x \right){{\rm{d}}_x}} 。$ | (17) |
满足约束条件:
| $ \int_R {f\left( x \right){{\rm{d}}_x}}=1 , $ | (18) |
| $ \int_R {{x^i}f\left( x \right) = {m_i}} ,i = 1,2, \cdots ,m, $ | (19) |
式中:f(x)为概率密度函数;R为积分区间;m为所用矩的阶数;mi为样本的第i阶原点矩。
通过调整p(x)使熵达到最大值,并采用拉朗日乘子法来求解此问题,得到概率密度函表达式:
| $ f\left( x \right) = \exp \left( {{\lambda _0} + \sum\limits_{i = 1}^n {{\lambda _i}{x^i}} } \right), $ | (20) |
式中,λ0, λ1, …, λm为拉格朗日乘子。
应用约束条件可得到λ0, λ1, …, λm所满足的方程:
| $ {m_i} = \frac{{\int_R {{x^i}\exp \left( {\sum\limits_{i = 1}^m {{\lambda _i}{x^i}} } \right){d_x}} }}{{\int_R {\exp \left( {\sum\limits_{i = 1}^m {{\lambda _i}{x^i}} } \right){d_x}} }}, $ | (21) |
| $ {\lambda _0} = - \ln \left( {\int_R {{x^i}\exp \left( {\sum\limits_{i = 1}^m {{\lambda _i}{x^i}} } \right){d_x}} } \right)。$ | (22) |
为了方便数值求解,将式(21)改写为
| $ 1 - \frac{{\int_R {{x^i}\exp \left( {\sum\limits_{i = 1}^m {{\lambda _i}{x^i}} } \right){d_x}} }}{{{m_i}\int_R {\exp \left( {\sum\limits_{i = 1}^m {{\lambda _i}{x^i}} } \right){d_x}} }} = {R_i}, $ | (23) |
式中Ri为残差。用非线性规划求残差平方和的最小值,得到其解为
| $ R = \sum\limits_{i = 1}^m {R_i^2 = \min } 。$ | (24) |
当R<ε或|Ri|<ε时,即认为上式收敛。这里ε是规定的允许误差。
2.3 拟合检验根据最大熵原理求得的最大熵密度函数选用精度高的K-S检验法(亦称d检验法)进行检验,将n个实验数据由小到大的次序排列,根据假设的分布,计算每个数据对应的F0(xi),再与经验分布函数Fn(xi)相比较。具体步骤为:
1) 设求得的最大熵密度函数式f(x)积分得到总体的概率分布函数为F(x),原假设:F(x)=F0(x);
2) 设经验概率分布函数为Fn(x),计算统计量
3) 取显著性水平α=0.10或α=0.05;
4) 根据α和样本容量n在K-S检验表上查得临界值Dn, α;
5) 统计推断:当Dn≤Dn, α时,则接受原假设分布;当Dn>Dn, α时,否定原假设,选用另一种概率分布。
3 基于Monte Carlo模拟法的可靠度计算方法 3.1 基本原理由大数定理,设x1, x2, …, xn是n个独立的随机变量,若它们来自同一母体,有相同的分布,且具有相同的均值和方差,用μ和σ2表示,则对于任意ε>0有
| $ \mathop {\lim }\limits_{n \to \infty } P\left\{ {\left| {\frac{1}{n}\sum\limits_{i = 1}^n {{x_i} - \mu } } \right| \ge \varepsilon } \right\} = 0。$ | (25) |
若随机事件A发生的概率为P(A),在n次独立试验中,事件A发生的频数为m,频率为W(A)=m/n,则对于任意ε>0有
| $ \mathop {\lim }\limits_{n \to \infty } P\left\{ {\left| {\frac{m}{n} - P\left( A \right)} \right| < \varepsilon } \right\} = 1。$ | (26) |
Monte Carlo模拟法计算结构可靠度的基本思路是先对随机变量进行大量抽样,再把这些抽样值代入结构功能函数式进行计算,然后统计失效个数,最后求得结构的可靠度。即:
| $ R = \frac{1}{N}\sum\limits_{i = 1}^N {I\left( X \right)} = \frac{1}{N}\sum\limits_{i = 1}^N {I\left( {{X_1},{X_2}, \cdots ,{X_n}} \right)} , $ | (27) |
式中,I(X)=I(X1, X2, …, Xn)为功能函数,由下式定义:
| $ I\left( X \right) = I\left( {{X_1},{X_2}, \cdots ,{X_n}} \right) = \left\{ \begin{array}{l} 1\;\;\;{\rm{if}}\;\;\;G\left( {{X_1},{X_2}, \cdots ,{X_n}} \right) > 0;\\ 0\;\;\;{\rm{if}}\;\;\;G\left( {{X_1},{X_2}, \cdots ,{X_n}} \right) \le 0。\end{array} \right. $ | (28) |
将N个随机数依次带入式()得满足事件的总和Ns,则:
| $ R = \frac{{{N_{\rm{s}}}}}{N}。$ | (29) |
对于边坡结构可靠性,可利用MATLAB软件编程进行计算,其计算步骤为:
1) 根据最大熵原理确定基本变量的分布函数、均值和标准差;
2) 用随机数发生器指令产生k′×l′的随机变量数组Xi(k, l)(i=1, 2, …, n);
3) 将各数组中元素代入功能函数F(c, γ),利用MATLAB数组运算中点乘除运算功能,得到功能函数结果数组F(c, γ)(k, l);
4) 统计功能函数结果数组中F(c, γ)(k, l)≥0元素个数P,可得可靠度为RS=P/(k×l)。
4 实例以湖南省长沙市望城区环线道路一边坡为例分析。该边坡为粉质粘土边坡,弹性模量E=7 MPa,泊松比μ=0.20,内摩擦角φ=25°,边坡高度H=30 m, 根据最大熵原理对参数γ,c进行统计推断,其统计特征如表 1所示。
| 表 1 随机变量统计参数 |
根据设计院的设计将边坡削坡至β=40°, 计算的可靠度R=0.766 9。工程实际中,可靠度太低。对现场进行了一段时间的观察,边坡有垮落的现象,边坡不稳定。然后调整参数进行可靠度计算,将边坡削坡β=30°,计算的可靠度R=0.997 2,对现场进行了2个月的观测,边坡稳定。
不同坡度下的可靠度值如表 2所示。
| 表 2 不同坡角下的可靠度值 |
不同模型下的可靠度曲线比较如图 2所示。
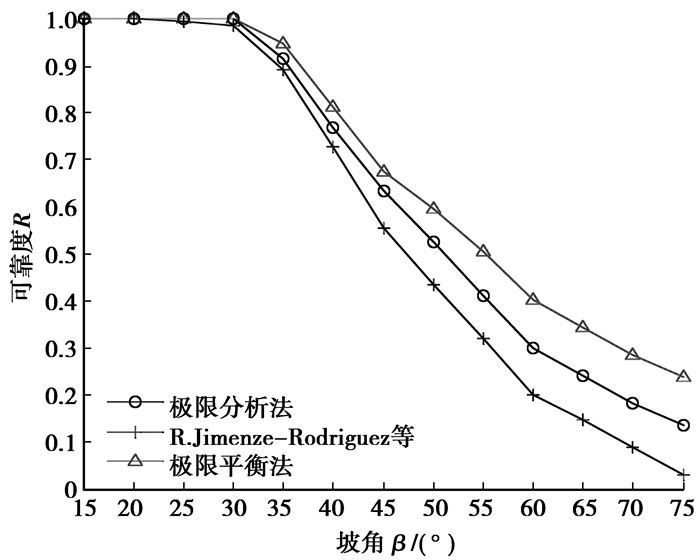
|
图 2 坡角与可靠度关系曲线 |
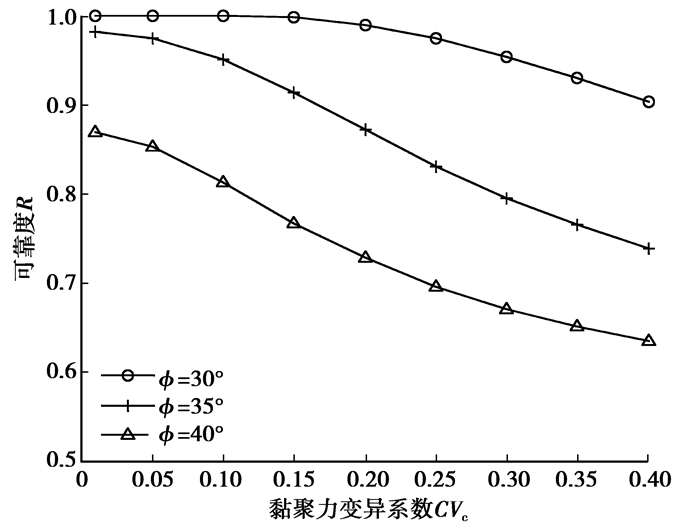
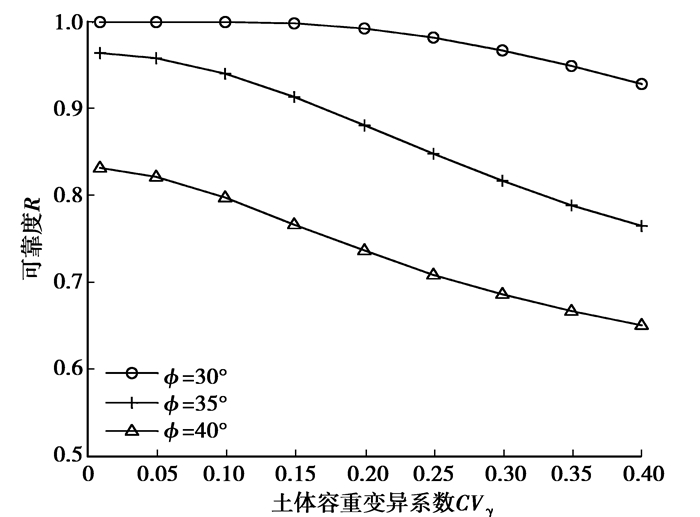
β=30°、ψ=35°、β=40°时各随机变量参数变化对可靠度的影响如图 3~图 6所示。
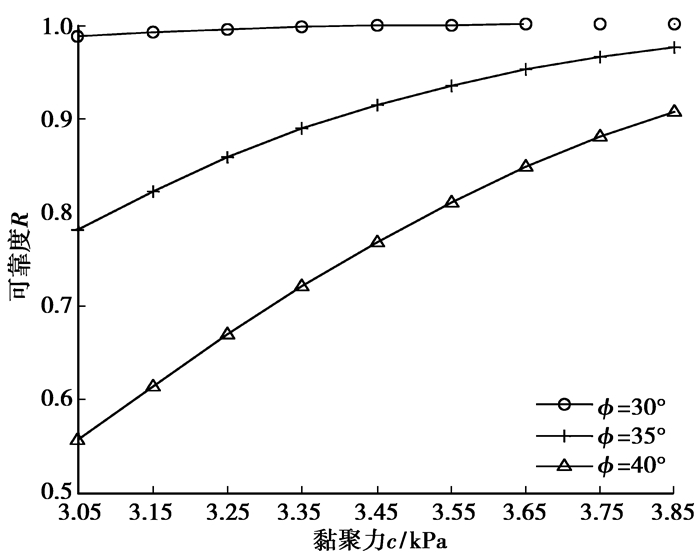
|
图 3 黏聚力与可靠度关系曲线 |
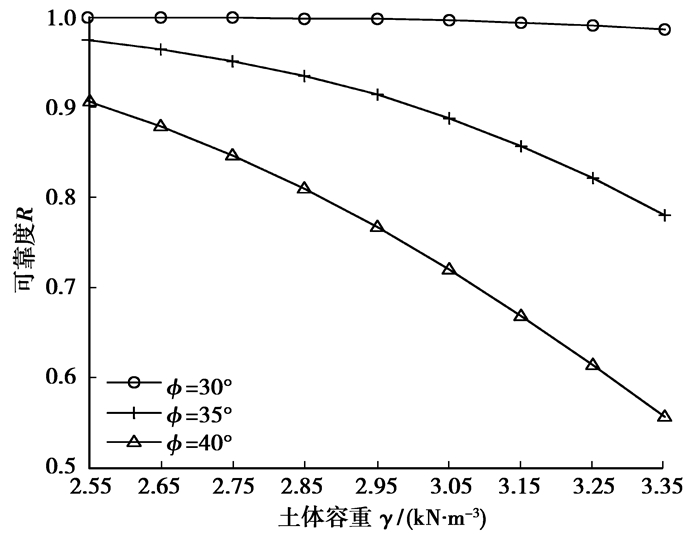
|
图 4 土体容重与可靠度关系曲线 |
|
图 5 黏聚力变异系数与可靠度关系曲线 |
|
图 6 土体容重变异系数与可靠度关系曲线 |
结果分析:
1) 文中模型与极限平衡法模型、R.Jimenez-Rodriguez等模型计算的结果比较接近。
2) 参数的离散性对结构可靠度具有明显影响,离散性越大,可靠度越低。
3) 粘聚力和土体容重是影响结构稳定的重要指标。
5 结论1) 建立了基于极限分析上限定理的边坡可靠度分析模型,并利用最大熵原理和Monte Carlo模拟法,在MATLAB环境下计算了边坡结构可靠度。该模型得到的可靠度值是边坡结构的一个严格上限,该上限值可作为评价边坡结构是否稳定的重要指标。
2) 文中得到的上限值从理论上应该大于或者等于真实值。该值比传统极限平衡法计算的值要小,与R.Jimenez-Rodriguez等模型计算的值比较接近,从而证明了该模型的科学性。
| [1] | Rodriguez R J, Sitar N, Chacon N. System reliability approach to rock slope stability[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(6): 847–859. |
| [2] | Rodriguez R J, Sitar N. Rock wedge stability analysis using system reliability methods[J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 419–427. DOI:10.1007/s00603-005-0088-x |
| [3] | Khaled F, Mounir L, Hedi H. Reliability analysis of slope stability using stochastic finite element method[J]. Procedia Engineering, 2011, 10: 1402–1407. DOI:10.1016/j.proeng.2011.04.233 |
| [4] |
谭晓慧, 王建国, 刘新荣, 等.
边坡稳定的有限元可靠度分析[J]. 重庆大学学报:自然科学版, 2006, 29(1): 102–104.
TAN Xiaohui, WANG Jianguo, LIU Xinrong, et al. Finite element reliability analysis of the stability of a slope[J]. Journal of Chongqing University:Natural Science Edition, 2006, 29(1): 102–104. (in Chinese) |
| [5] | Yang X L, Huang F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion[J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686–691. DOI:10.1016/j.tust.2011.05.008 |
| [6] | Yang X L. Seismic passive pressures of earth structures by nonlinear optimization[J]. Archive of Applied Mechanics, 2011, 81(9): 1195–1202. DOI:10.1007/s00419-010-0478-8 |
| [7] | Yang X L, Wang J M. Ground movement prediction for tunnels using simplified procedure[J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462–471. DOI:10.1016/j.tust.2011.01.002 |
| [8] | Saada Z, Maghous S, Garnier D. Stability analysis of rock slopes subjected to seepage forces using the modified Hoek-Brown criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 55(1): 45–54. |
| [9] | Li A J, Merifield R S, Lyamin A V. Limit analysis solutions for three dimensional undrained slopes[J]. Computers and Geotechnics, 2009, 36(8): 1330–1351. DOI:10.1016/j.compgeo.2009.06.002 |
| [10] | Li A J, Lyamin A V, Merifield R S. Seismic rock slope stability charts based on limit analysis methods[J]. Computers and Geotechnics, 2009, 36(1/2): 135–148. |
| [11] |
李东升, 刘东升, 王渝昆.
煤矿区矸石山塑性极限可靠度分析[J]. 重庆大学学报, 2008, 31(12): 1441–1445.
LI Dongsheng, LIU Dongsheng, WANG Yukun. Plastic upper bound theory reliability analysis of coal gangue hills[J]. Journal of Chongqing University, 2008, 31(12): 1441–1445. (in Chinese) |
| [12] |
邓建, 李夕兵, 古德生.
岩石力学参数概率分布的信息熵推断[J]. 岩石力学与工程学报, 2004, 23(13): 2177–2181.
DENG Jian, LI Xibing, GU Desheng. Probability distribution of rock mechanics parameters by using maximum entropy method[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(13): 2177–2181. DOI:10.3321/j.issn:1000-6915.2004.13.008 (in Chinese) |
| [13] |
张道兵, 杨小礼, 朱川曲, 等.
基于最大熵原理与最优化方法的隧道衬砌结构可靠度分析[J]. 中南大学学报, 2012, 43(2): 663–668.
ZHANG Daobing, YANG Xiaoli, ZHU Chuanqu, et al. Structural reliability analysis of tunnel lining based on maximal entropy principle and optimization method[J]. Journal of Central South University, 2012, 43(2): 663–668. (in Chinese) |
| [14] | Pandry M D. Direct estimation of quantile functions using the maximum entropy principle[J]. Structural Safety, 2000, 22(1): 61–79. DOI:10.1016/S0167-4730(99)00041-7 |
| [15] | Sobczyk K, Trebicki J. Approximate probability distributions for stochastic systems:maximum entropy method[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 168(1/4): 91–111. |
| [16] | Gilles M. Uncertainty interval expression of measurement:possibility maximum specificity versus probability maximum entropy principles[J]. Communications in Computer and Information Science, 2010, 80(1): 386–395. |
| [17] | Cho S E. First-order reliability analysis of slope considering multiple failure modes[J]. Engineering Geology, 2013, 154: 98–105. DOI:10.1016/j.enggeo.2012.12.014 |
| [18] | Cho S E. Probabilistic stability analyses of slopes using the ANN-based response surface[J]. Computers and Geotechnics, 2009, 36(5): 787–797. DOI:10.1016/j.compgeo.2009.01.003 |
| [19] | Cardoso J B, Almeida J R, Dias J M, et al. Structure reliability analysis using Monte Carlo simulation and neural networks[J]. Advances in Engineering Software, 2008, 39: 505–513. DOI:10.1016/j.advengsoft.2007.03.015 |
| [20] | Wang Y, Cao Z J, Au S K. Efficient monte carlo simulation of parameter sensitivity in probabilistic slope stability analysis[J]. Computers and Geotechnics, 2010, 37(7/8): 1015–1022. |
| [21] | Zhang H, Dai H Z, Beer M, et al. Structural reliability analysis on the basis of small samples:An interval quasi-monte carlo method[J]. Mechanical Systems and Signal Processing, 2013, 37(1/2): 137–151. |
| [22] | Chen W F. Limit analysis and soil plasticity[M]. Amsterdam: Elsevier Scientific Publishing Company, 1975: 275-306. |
 2014, Vol. 37
2014, Vol. 37


