b. 重庆大学 重庆市冶金工程重点实验室, 重庆 400044;
c. 重庆大学 化学化工学院, 重庆 400044
b. Chongqing Provincial Key Laboratory of Metallurgical Engineering, Chongqing University, Chongqing 400044, China;
c. School of Chemistry and Chemical Engineering, Chongqing University, Chongqing 400044, China
在本研究的第一部分[1]中,首先将动力学稳态近似法中经常应用的浓度随时间不变的稳态假设发展为浓度变化率随时间不变的稳态假设,以质量守衡原理、菲克扩散定律为物理基础,以对方程的离散化处理为手段,以浓度变化率随时间不变为稳态约束,给出了对有限长度区间内扩散方程进行稳态近似法处理的过程;同时获得了二、三类边界条件下区间(0,l)内任一位置x处初始浓度都为零的扩散方程的一个稳态近似解cx:
| $ {c_x} = - \left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}{{\rm{e}}^{{r_1}t}} + \left[ {{r_1} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}{{\rm{e}}^{{r_2}t}} + {c^0}, $ | (1) |
其中:
| $ {r_1} = \frac{{ - l\left( {l\beta + 2D} \right) - \sqrt {{l^2}{{\left( {l\beta + 2D} \right)}^2} - 8x\left( {l - x} \right)\left( {l + \frac{1}{2}lx\frac{\beta }{D} - \frac{1}{6}{x^2}\frac{\beta }{D}} \right)\beta D} }}{{2x\left( {l - x} \right)\left( {l + \frac{1}{2}lx\frac{\beta }{D} - \frac{1}{6}{x^2}\frac{\beta }{D}} \right)}}, $ |
| $ {r_2} = \frac{{ - l\left( {l\beta + 2D} \right) + \sqrt {{l^2}{{\left( {l\beta + 2D} \right)}^2} - 8x\left( {l - x} \right)\left( {l + \frac{1}{2}lx\frac{\beta }{D} - \frac{1}{6}{x^2}\frac{\beta }{D}} \right)\beta D} }}{{2x\left( {l - x} \right)\left( {l + \frac{1}{2}lx\frac{\beta }{D} - \frac{1}{6}{x^2}\frac{\beta }{D}} \right)}}, $ |
式中:D为扩散系数;β为对流传质系数。笔者对该稳态近似解进行了分析,并与准确度很高的数值解进行了比较。
1 区间端点的近似解本研究获得x处的近似值cx的过程中,x没有取区间端点的坐标0或l,因此不能直接利用式(1)计算0或l处的近似值。当t>0时:
| $ \begin{array}{l} \mathop {\lim }\limits_{x \to 0} {c_x} = - \mathop {\lim }\limits_{x \to 0} \left\{ {\left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{t \cdot \mathop {\lim r1}\limits_{x \to 0} }} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathop {\lim }\limits_{x \to 0} \left\{ {\left[ {{r_1} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{t \cdot \mathop {\lim r2}\limits_{x \to 0} }} + {c^0}\\ \;\;\;\;\;\;\;\;\;\;\;\; = - \frac{{2D}}{{l\beta + 2D}}{c^0}{{\rm{e}}^{ - \frac{{2D}}{{l\beta + 2D}}\frac{\beta }{l}t}} + {c^0}。\end{array} $ |
所以t时刻(t>0)端点(x=0处)的近似值(c0)t,可取为
| $ {\left( {{c_0}} \right)_t} = - \frac{{2D}}{{l\beta + 2D}}{c^0}{{\rm{e}}^{ - \frac{{2D}}{{l\beta + 2D}}\frac{\beta }{l}t}} + {c^0}。$ | (2) |
因为:
| $ \begin{array}{l} \mathop {\lim }\limits_{\begin{array}{*{20}{c}} {x \to 0}\\ {t \to 0} \end{array}} {c_x} = - \mathop {\lim }\limits_{x \to 0} \left\{ {\left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{\mathop {\lim }\limits_{t \to 0} t \cdot \mathop {\lim r_1}\limits_{x \to 0} }} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathop {\lim }\limits_{x \to 0} \left\{ {\left[ {{r_1} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{\mathop {\lim }\limits_{t \to 0} t \cdot \mathop {\lim r_2}\limits_{x \to 0} }} + {c^0}\\ \;\;\;\;\;\;\;\;\;\;\;\; = - \frac{{l\beta }}{{l\beta + 2D}}{c^0}{{\rm{e}}^{ - \frac{{l\beta + 2D}}{l}}} - \frac{{2D}}{{l\beta + 2D}}{c^0} + {c^0}, \end{array} $ |
所以t=0时刻端点(x=0处)的近似值(c0)0,可取为
| $ {\left( {{c_0}} \right)_0} = \mathop {\lim }\limits_{\begin{array}{*{20}{c}} {x \to 0}\\ {t \to 0} \end{array}} {c_x} = - \frac{{l\beta }}{{l\beta + 2D}}{{\rm{e}}^{ - \frac{{l\beta + 2D}}{l}}} \cdot {c^0} - \frac{{2D}}{{l\beta + 2D}} \cdot {c^0} + {c^0}. $ | (3) |
同样地,可以得到t>0时,x=l端点的近似值(cl)t为
| $ {\left( {{c_l}} \right)_t} = - {c^0}{{\rm{e}}^{ - \frac{{2D}}{{l\beta + 2D}}\frac{\beta }{l}t}} + {c^0}, $ | (4) |
可以得到t=0时刻端点(x=l处)的近似值(cl)0为
| $ {\left( {{c_l}} \right)_0} = 0, $ | (5) |
在式(4)中,令t=0的结果为0,刚好和式(5)的结果一致,综合式(4)和式(5),得端点(x=l处)近似值cl为
| $ {c_l} = - {c^0}{{\rm{e}}^{ - \frac{{2D}}{{l\beta + 2D}}\frac{\beta }{l}t}} + {c^0}. $ | (6) |
式(3)的结果大于零;在式(2)中令t=0获得的值大于零,和式(3)的结果也不一致。x=0处的零时刻浓度不为零,且零时刻浓度随时间变化不连续,原因是在左端点采用的边界条件[1]为
| $ D\frac{{\partial c}}{{\partial x}}\left| {_{x = 0}} \right. = \beta \left( {c\left| {_{x = 0}} \right. - {c^0}} \right). $ |
该式中没有非稳态项,意味着在左边界端点发生的不是物质由零连续积累的非稳态过程,而是瞬间达到稳态的过程。令t→0而获得x=0处的零时刻浓度的时候,即由扩散发生后向扩散初始时刻逼近时,其极限值可不为零;零时刻浓度随时间变化也不一定连续。
2 一、二类边界条件下的一个近似解式(1)是扩散方程在二、三类边界条件下,按照本研究第一部分中给出的稳态近似法处理过程[1],而获得的近似解。对其他边界条件下的扩散方程,同样也可按照相同的处理过程获得近似解。不过,注意到扩散方程在二、三类边界条件下,当l、D不变,β→∞(即D/lβ→0)时,外部对流传质阻力趋于零,扩散区间左端点浓度始终等于外介质浓度c0,这时第三类边界条件等同于第一类边界条件。因此可由式(1)推得扩散方程在一、二类边界条件下的一个近似解。式(1)中r1、r2、
| $ {r_1} = \frac{{ - l\left( {1 + 2\frac{D}{{l\beta }}} \right) - \sqrt {{l^2}{{\left( {1 + 2\frac{D}{{l\beta }}} \right)}^2} - 8x\left( {l - x} \right)\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2x\left( {l - x} \right)\frac{l}{D}\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)}}, $ |
| $ {r_2} = \frac{{ - l\left( {1 + 2\frac{D}{{l\beta }}} \right) + \sqrt {{l^2}{{\left( {1 + 2\frac{D}{{l\beta }}} \right)}^2} - 8x\left( {l - x} \right)\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2x\left( {l - x} \right)\frac{l}{D}\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)}}, $ |
| $ \begin{array}{*{20}{c}} {\left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}} = }\\ {\frac{{2\left( {l - x} \right)\left( {1 - \frac{x}{l}} \right) - l\left( {1 + 2\frac{D}{{l\beta }}} \right) + \sqrt {{l^2}{{\left( {1 + 2\frac{D}{{l\beta }}} \right)}^2} - 8x\left( {l - x} \right)\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2\sqrt {{l^2}{{\left( {1 + 2\frac{D}{{l\beta }}} \right)}^2} - 8x\left( {l - x} \right)\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{c^0},} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\left[ {{r_1} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}} = }\\ {\frac{{2\left( {l - x} \right)\left( {1 - \frac{x}{l}} \right) - l\left( {1 + 2\frac{D}{{l\beta }}} \right) - \sqrt {{l^2}{{\left( {1 + 2\frac{D}{{l\beta }}} \right)}^2} - 8x\left( {l - x} \right)\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2\sqrt {{l^2}{{\left( {1 + 2\frac{D}{{l\beta }}} \right)}^2} - 8x\left( {l - x} \right)\left( {\frac{D}{{l\beta }} + \frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{c^0}。} \end{array} $ |
当l、D不变,β→∞(即
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{\beta \to \infty \left( {{\rm{or}}\frac{D}{{l\beta }} \to 0} \right)} {c_x} = - \frac{{2\left( {l - x} \right)\left( {1 - \frac{x}{l}} \right) - l + \sqrt {{l^2} - 8x\left( {l - x} \right)\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2\sqrt {{l^2} - 8x\left( {l - x} \right)\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{c^0}{{\rm{e}}^{\frac{{ - l - \sqrt {{l^2} - 8x\left( {l - x} \right)\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2x\left( {l - x} \right)\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)}}Dt}} + }\\ {\frac{{2\left( {l - x} \right)\left( {1 - \frac{x}{l}} \right) - l - \sqrt {{l^2} - 8x\left( {l - x} \right)\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2\sqrt {{l^2} - 8x\left( {l - x} \right)\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{c^0}{{\rm{e}}^{\frac{{ - l + \sqrt {{l^2} - 8x\left( {l - x} \right)\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)} }}{{2x\left( {l - x} \right)l\left( {\frac{1}{2}\frac{x}{l} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}} \right)}}Dt}} + {c^0}.} \end{array} $ | (7) |
式(7)作为一个稳态近似解,对应的非稳态扩散问题为
| $ \frac{{\partial c}}{{\partial t}} = D\frac{{{\partial ^2}c}}{{\partial {x^2}}}, $ |
初始条件t=0:x∈(0, l), c=0;
边界条件t>0:x=0,
因也不能直接用式(7)计算在端点的近似值,令x→0、x→l可得到一、二类边界条件下,端点浓度的(近似)值。
| $ \mathop {\lim }\limits_{x \to 0} \left[ {\mathop {\lim }\limits_{\beta \to \infty \left( {{\rm{or}}\frac{D}{{l\beta }} \to 0} \right)} {c_x}} \right] = {c^0}, $ | (8) |
| $ \mathop {\lim }\limits_{x \to l} \left[ {\mathop {\lim }\limits_{\beta \to \infty \left( {{\rm{or}}\frac{D}{{l\beta }} \to 0} \right)} {c_x}} \right] = - {c^0}{{\rm{e}}^{ - \frac{{2D}}{{{l^2}}}t}} + {c^0}。$ | (9) |
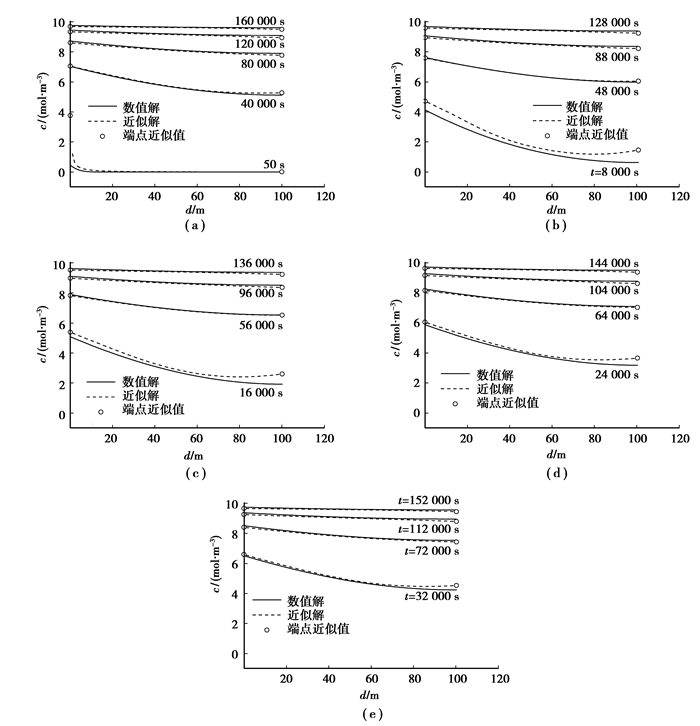
数值方法是求解传输方程普遍应用的方法;对扩散方程来讲,它的数值方法发展得最成熟。对前述非稳态扩散问题,取c0= 10 mol/m3,l=100 m,D=0.25 m2/s,β=0.003 m/s;按照通常的数值方法[2]获得它的数值解,计算数值解时,均匀网格数取1 000 (即网格宽度=0.1 m),时间步长取1 s。网格再加密,时间步长再缩短,均看不出数值解再有变化,这时的数值解其实就可看作是前述非稳态问题的精确解。数值解用图 1、图 2中的实线示出。按式(1)近似解cx的表达式计算的结果用图 1中虚线示出。按式(7)近似解
|
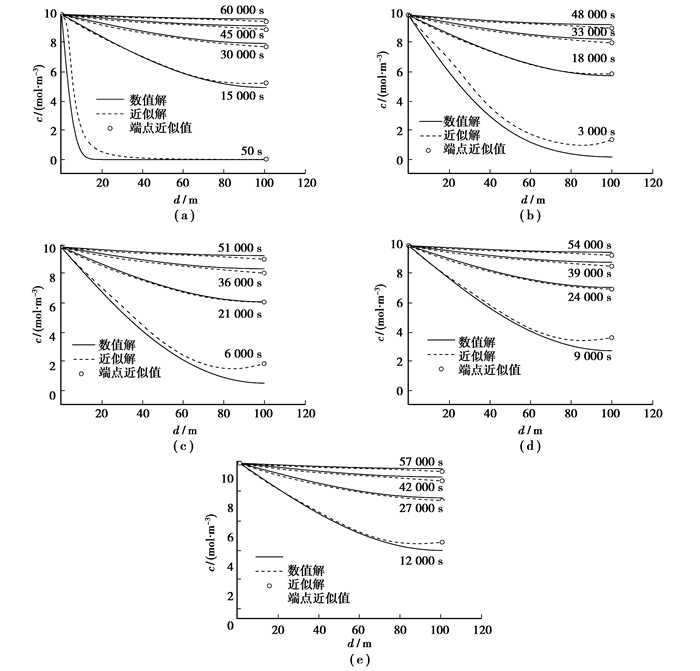
图 1 二、三类边界条件下数值解和近似解的对比图 |
|
图 2 一、二类边界条件下扩散方程数值解和近似解的对比图 |
从近似解和数值解对比可以看出:在扩散开始后会存在一个时间段,如图 1中的48 000~56 000 s期间、图 2中的18 000~21 000 s期间,在此时间段里,近似解和数值解曲线形状吻合最好;从初始时刻到进入两者吻合最好期间的过程中,如在图 1的0~48 000 s期间、图 2的0~18 000 s期间,近似解曲线位于数值解曲线上方,两者差值由初始时刻的零逐渐增大,到中间某阶段(如图 1的8 000~16 000 s、图 2的3 000~9 000 s)达到最大,然后逐渐减小,到进入两者吻合最好期间基本减为0;在两者吻合最好期间过后,近似解曲线位于数值解曲线下方,但两者差值不大,且两者差值随时间变化不明显。总体来说,图 1的8 000~24 000 s时间段、图 2的3 000~12 000 s时间段,近似解和数值解相差稍大,但在其他时刻两者吻合程度是较好的。
另外,从扩散开始到最终达到稳态的漫长时间里(图 1、图 2是算例条件下的结果,如选固态金属中的扩散来计算,扩散时间更是漫长的),近似解和数值解是同步的,因此用此近似解预测达到最终稳态的时间,准确度应该是好的;从图 1可以看出,浓度变化率随时间不变的稳态假设约束,对浓度随时间变化节奏的影响是较小的:在0~48 000 s期间,近似解随时间变化稍快;在48 000~56 000 s期间,近似解基本完全体现了浓度随时间变化的节奏;在56 000 s之后,虽然近似解稍小于数值解,但两者差值随时间没有明显变化,近似解和数值解随时间变化的节奏基本是相同的。总体来说:近似解是可以接受的。扩散方程分析解的稳态近似法可以说是有效的。
若在获得前述非稳态问题近似解的过程中,稳态假设改为c1=const,即dc1/dt=0;cl, 1=const,即dcl, 1/dt=0,按照本研究第一部分叙述的方法和步骤[1],最终可得到的近似解为:cx=c0。这说明在各时刻近似解cx的值都是最终稳态的值。这个近似解和实际情形差别就大了。但工程上得到应用的金属氧化模型、未反应核模型等都是在假设产物层氧化或还原气体浓度c=const得到的,所以cx的这个结果会有它的启示和比较的作用,也称之为近似解。浓度不随时间变化稳态假设下的近似解就是最终稳态的解,意味着稳态近似法处理的结果可能首先从近似最终稳态开始,然后可能接着近似接近最终稳态的状态,再接着可能近似远离最终稳态的状态。图 1、图 2中出现的近似解和数值解吻合现象在较大程度上支持这种理解。与这种理解不一致的是:最大的近似解与数值解之差并没有出现在离最终稳态最远的初始时刻。由获得近似解的过程看,随时间变化的稳态近似解所采用的初始条件和数值解是相同的,即近似解和数值解在零时刻都取任何位置的浓度为零。因此扩散开始一段时间后,最大的近似解与数值解之差才会出现。
稳态近似解能很好地预测达到最终稳态的时间和最终的稳态;近似解和数值解的初始条件又是相同的。在初始时刻和最终稳态,近似解和数值解是相同的。这是稳态近似解和数值解随时间同步变化的重要保证。
另外,从图 1、图 2还可以看出,近似解基本上是遵循总体质量守恒的,就是说同一时刻近似解曲线和数值解曲线下的面积是相差不大的。但近似解曲线下面的面积和数值解曲线下面的面积在图 1的8 000、16 000、24 000 s时刻、图 2的3 000、6 000、9 000 s时刻是有稍大些的差别。近似解基本上是遵循总体质量守恒的,这也可由近似解和数值解是同步的结论意识到;而图 1的8 000、16 000、24 000 s时刻、图 2的3 000、6 000、9 000 s时刻近似解满足总体质量守恒程度稍差是由稳态近似法的特点决定的,稳态近似法处理的结果首先从近似最终稳态开始。
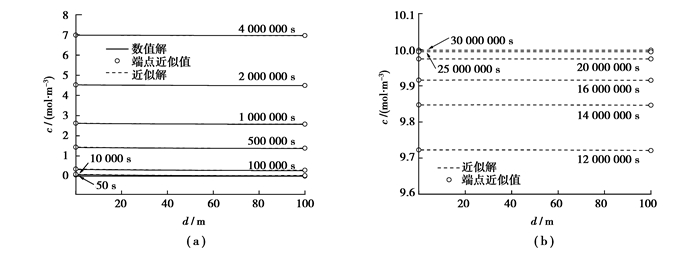
4 低lβ/D数下近似解与数值解、精确解的对比对式(1)近似解所对应的非稳态扩散问题,取c0= 10 mol/m3,l=100 m,β=0.000 03 m/s,D=0.25 m2/s;按照同样的数值方法(均匀网格宽度=0.1 m,时间步长取1 s)获得的数值解和按式(1)、式(2)、式(6)获得的近似解对比见图 3(a);由图看出,近似解和数值解各时刻基本完全重合,两者基本都呈水平直线;由近似解计算式获得的接近最终稳态的几个时刻浓度分布见图 3(b), 由图可判断, 达到最终稳态需要约30 000 000 s。
|
图 3 低lβ/D数下数值解和近似解的对比图 |
此例下,lβ/D=(100×0.000 03)/0.25=0.012,外部对流传质占统治地位。由传质理论知道在lβ/D→0下,(0, l)内浓度分布均匀,且浓度随时间变化关系为
| $ {c_x}\left( t \right) = - {c^0}{{\rm{e}}^{ - \frac{\beta }{l}t}} + {c^0}。$ | (10) |
由式(1)的近似式出发同样可以推出这一结果。
式(1)中r1、r2、
| $ {r_1} = \frac{{ - l\left( {\frac{{l\beta }}{D} + 2} \right) - \sqrt {{l^2}{{\left( {\frac{{l\beta }}{D} + 2} \right)}^2} - 8x\left( {l - x} \right)\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]} }}{{2x\left( {l - x} \right)\frac{1}{\beta }\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]}}, $ |
| $ {r_2} = \frac{{ - l\left( {\frac{{l\beta }}{D} + 2} \right) + \sqrt {{l^2}{{\left( {\frac{{l\beta }}{D} + 2} \right)}^2} - 8x\left( {l - x} \right)\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]} }}{{2x\left( {l - x} \right)\frac{1}{\beta }\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]}}, $ |
| $ \begin{array}{*{20}{c}} {\left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}} = }\\ {\frac{{2\frac{{l\beta }}{D}\frac{{{{\left( {l - x} \right)}^2}}}{l} - l\left( {\frac{{l\beta }}{D} + 2} \right) + \sqrt {{l^2}{{\left( {\frac{{l\beta }}{D} + 2} \right)}^2} - 8x\left( {l - x} \right)\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]} }}{{2\sqrt {{l^2}{{\left( {\frac{{l\beta }}{D} + 2} \right)}^2} - 8x\left( {l - x} \right)\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]} }}{c^0},} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\left[ {{r_1} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}} = }\\ {\frac{{2\frac{{l\beta }}{D}\frac{{{{\left( {l - x} \right)}^2}}}{l} - l\left( {\frac{{l\beta }}{D} + 2} \right) - \sqrt {{l^2}{{\left( {\frac{{l\beta }}{D} + 2} \right)}^2} - 8x\left( {l - x} \right)\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]} }}{{2\sqrt {{l^2}{{\left( {\frac{{l\beta }}{D} + 2} \right)}^2} - 8x\left( {l - x} \right)\left[ {\frac{{l\beta }}{D} + \frac{1}{2}\frac{x}{l}{{\left( {\frac{{l\beta }}{D}} \right)}^2} - \frac{1}{6}\frac{{{x^2}}}{{{l^2}}}{{\left( {\frac{{l\beta }}{D}} \right)}^2}} \right]} }}{c^0}。} \end{array} $ |
当t>0,l、β不变时:
| $ \begin{array}{l} \mathop {\lim }\limits_{D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} {c_x} = - \mathop {\lim }\limits_{D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \left\{ {\left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{t \cdot \mathop {\lim }\limits_{\begin{array}{*{20}{c}} {D \to \infty }\\ {\left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \end{array}} {r_1}}} + \\ \mathop {\lim }\limits_{D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \left\{ {\left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{t \cdot \mathop {\lim }\limits_{\begin{array}{*{20}{c}} {D \to \infty }\\ {\left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \end{array}} {r_2}}} + {c^0} = - {c^0}{{\rm{e}}^{ - \frac{\beta }{l}t}} + {c^0}。\end{array} $ |
所以D→∞时,t(t>0)时刻x处的近似值(cx)t为
| $ {\left( {{c_x}} \right)_t} = - {c^0}{{\rm{e}}^{ - \frac{\beta }{l}t}} + {c^0}: $ | (11) |
当l、β不变时:
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{\begin{array}{*{20}{c}} {t \to 0}\\ {D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \end{array}} {c_x} = - \mathop {\lim }\limits_{D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \left\{ {\left[ {{r_2} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{\mathop {\lim }\limits_{t \to 0} t\mathop {\lim {r_1}}\limits_{D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} }} + }\\ {\mathop {\lim }\limits_{D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \left\{ {\left[ {{r_1} + \frac{{\beta \left( {l - x} \right)}}{{x\left( {l + \frac{\beta }{{2D}}lx - \frac{\beta }{{6D}}{x^2}} \right)}}} \right]\frac{{{c^0}}}{{{r_2} - {r_1}}}} \right\} \cdot {{\rm{e}}^{\mathop {\lim }\limits_{t \to 0} t\mathop {\lim {r_2}}\limits_{D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} }} + {c^0} = 0,} \end{array} $ |
所以D→∞时,t=0时刻x处的近似值(cx)0为
| $ {\left( {{c_x}} \right)_0} = \mathop {\lim }\limits_{\begin{array}{*{20}{c}} {t \to 0}\\ {D \to \infty \left( {{\rm{or}}\frac{{l\beta }}{D} \to 0} \right)} \end{array}} {c_x} = 0, $ | (12) |
综合式(11)、式(12)可得,当l、β不变,D→∞时x处近似值cx为
| $ {c_x} = - {c^0}{{\rm{e}}^{ - \frac{\beta }{l}t}} + {c^0}. $ | (13) |
这与理论分析结果式(10)是一致的。
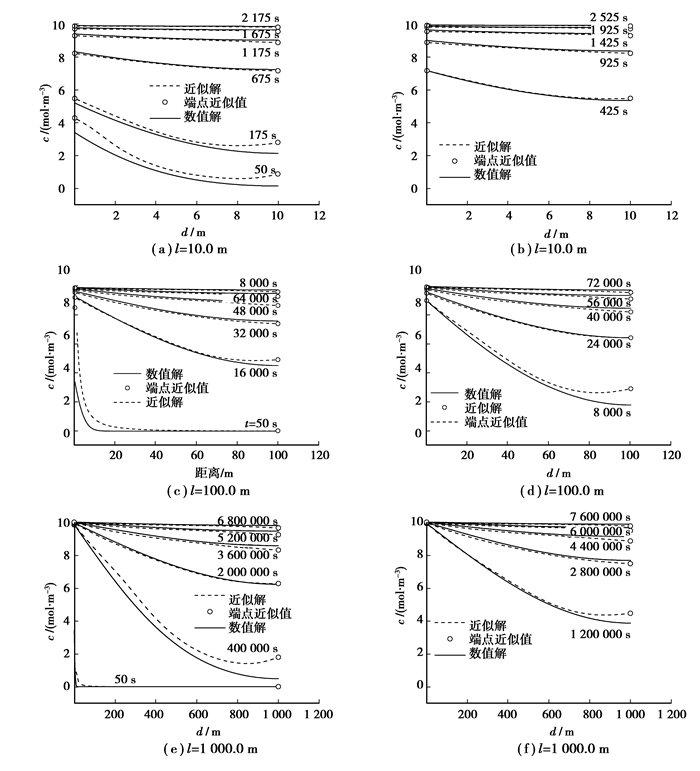
5 扩散区间长度l的影响取c0= 10 mol/m3,D=0.25 m2/s,β=0.03 m/s,l分别取10、100、1 000 m。按式(1)、式(2)、式(6)近似解cx表达式计算的结果,按数值方法(均匀网格宽度为0.1 m,时间步长取1 s)计算的结果示于图 4中。从对3个不同扩散区间长度的计算结果同样可以看出近似解和数值解吻合的特点。
|
图 4 扩散区间长度l的影响 |
1) 存在一段吻合最好期(在图 4(a)、(b)中425~675 s,图 4(d)中24 000 s,图 4(e)中2 000 000 s)且在吻合最好期之前,近似解基本大于数值解;在吻合最好期之后,近似解小于数值解,但两者相差不大。
2) 离最终稳态越近,稳态近似解越精确。
3) 近似解和数值解随时间变化是同步的。稳态近似解和精确解在初始时刻和最终稳态是相同的是这一吻合特点的重要保证。
另外稳态近似解定性上体现了扩散长度对扩散过程的影响。在其他条件不变的情况下,l逐渐变大,lβ/D逐渐变大,相对于对流传质,(0, l)内扩散逐渐变地占控制地位。图 4中扩散区间左端点浓度[由式(2)计算]变化体现了这一点。图 4(a)、(b)中,扩散长度较小,对流传质占控制地位,区间左端点浓度随时间变化的强度随对流传质由强变弱的变化而变化;图 4(e)、(f)中,扩散长度较大,对流传质速率比内部扩散速率大的多,区间左端点浓度基本不随时间变化,且维持在外介质浓度。
6 进一步提高稳态近似解精度的初步分析对扩散方程的处理,说明本研究对传统稳态假设[3-5]的发展是合理的;可考虑利用发展后的假设内容对块矿、球团等的反应[6-15]建立更准确的模型。将ci=const假设发展为dci/dt=const的假设,可提高稳态近似法处理问题的精度;按此逻辑,将dci/dt=const假设发展为d2ci/dt2=const的假设,可进一步提高稳态近似法的精度。但就非稳态扩散问题来说,它的初始条件通常都是给定初始时刻的浓度值,不会再进一步给定初始时刻浓度变化率的值。由于缺乏定解条件,因此通过将dci/dt=const假设发展为d2ci/dt2=const的假设来提高扩散方程稳态近似解的精度是不可行的。在dci/dt=const假设下,本研究通过同时求解关于浓度c1、cl, 1的两个常微分方程[1]来获得近似解。笔者认为提高近似解精度的途径为:通过对扩散项采用更高精度的离散格式[2],将任一位置的扩散通量离散为关于更多节点上浓度的离散式;最后仍然在dci/dt=const假设下,通过同时求解3个(或4个、或5个)常微分方程来获得近似解。
7 结论1) 稳态近似解全面地反映了传质参数或准数对传质过程的定性影响。通过与有足够精度的数值解对比得出:稳态近似法获得的结果基本上满足总体质量守恒;从扩散开始,一直到最终稳态的过程中,稳态近似法获得的结果和精确解是同步的;稳态近似法获得的结果与接近最终稳态的情形吻合程度好,与远离最终稳态的情形吻合程度差些。
2) 在lβ/D→0的情况下,从稳态近似解导出的结果与理论分析结果完全一致。
3) 对扩散方程的稳态近似法处理过程和由此获得的近似解工程上可以应用。该稳态近似处理过程也可以处理对流扩散方程、导热方程等。
| [1] | WANG Chengshan, LI Dandan, SHI Yanwen, et al. Analysis of diffusion equation based on steady state assumption:Ⅰ.the process of steady state approximation[J]. Journal of Chongqing University, 2014, 37(5): 53–63. |
| [2] | 陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001: 33-90. |
| [3] | 黄希祜. 钢铁冶金原理[M]. 北京: 冶金工业出版社, 2005: 67-87. |
| [4] | 王淑兰. 物理化学[M]. 3版.北京: 冶金工业出版社, 2008: 219-220. |
| [5] | 梁英教. 物理化学[M]. 北京: 冶金工业出版社, 2005: 272-274. |
| [6] | Kuwauchi Y, Barati M. A mathematical model for carbothermic reduction of dust-carbon composite agglomerates[J]. ISIJ International, 2013, 53(6): 1097–1105. DOI:10.2355/isijinternational.53.1097 |
| [7] | Kim D Y, Heo Y U, Sasaki Y. Cementite formation from magnetite under high pressure conditions[J]. ISIJ International, 2013, 53(6): 950–957. DOI:10.2355/isijinternational.53.950 |
| [8] | Bonalde A, Henriquez A, Manrique M. Kinetic analysis of the iron oxide reduction using hydrogen-carbon monoxide mixtures as reducing agent[J]. ISIJ international, 2005, 45: 1255–1260. DOI:10.2355/isijinternational.45.1255 |
| [9] | Mousa E A, Babich A, Senk D. Enhancement of iron ore sinter reducibility through coke oven gas injection into the modern blast furnace[J]. ISIJ International, 2013, 53(8): 1372–1380. DOI:10.2355/isijinternational.53.1372 |
| [10] | Sohn H Y, Perez F S. Application of the law of additive reaction times to fluid-solid reactions in porous pellets with changing effective diffusivity[J]. Metallurgical and Materials Transactions B, 2010, 41(6): 1261–1267. DOI:10.1007/s11663-010-9414-0 |
| [11] | Noguchi D, Ohno K, Maeda T, et al. Effect of CO gas concentration on reduction rate of major mineral phase in sintered iron ore[J]. ISIJ International, 2013, 53(4): 570–575. DOI:10.2355/isijinternational.53.570 |
| [12] | Wu S L, Xu J, Yang S D, et al. Basic characteristics of the shaft furnace of COREX smelting reduction process based on iron oxides reduction simulation[J]. ISIJ international, 2010, 50(7): 1032–1039. DOI:10.2355/isijinternational.50.1032 |
| [13] | Yang K, Choi S, Chung J, et al. Numerical modeling of reaction and flow characteristics in a blast furnace with consideration of layered burden[J]. ISIJ international, 2010, 50(7): 972–980. DOI:10.2355/isijinternational.50.972 |
| [14] | Dong X F, Yu A B, Yagi J, et al. Modelling of multiphase flow in a blast furnace:recent developments and future work[J]. ISIJ international, 2007, 47(11): 1553–1570. DOI:10.2355/isijinternational.47.1553 |
| [15] | Chuang H C, Kuo J H, Huang C C, et al. Multi-phase flow simulations in direct iron ore smelting reduction process[J]. ISIJ international, 2006, 46(8): 1158–1164. DOI:10.2355/isijinternational.46.1158 |
 2014, Vol. 37
2014, Vol. 37

