随着计算机系统复杂性的不断增加,传统冯诺依曼体系的计算机在指令的顺序存取、译码、执行方面都遭遇到了其执行效率低下的瓶颈问题。如今的数字计算机已经拥有了模拟低等动物大脑功能的计算速度和系统复杂度,但随着计算机计算速度的提高相关的能量消耗与系统的复杂度将会呈指数形式上升。生物大脑的结构显然不同于传统的冯诺依曼结构的计算机,生物大脑处理问题的高效率关键在于庞大数量的神经元以及它们之间的连接,这种复杂的连接极大的提高了生物大脑的并行计算能力[1]。按照国际半导体技术发展路线图预测,到2020年晶体管的集成度会达到1010个/cm2。即便如此,要建立人类大脑模型,解决神经元之间的连接是一个十分困难但迫切的问题。
1971年,蔡少棠教授在电路完备性理论的基础上阐述和定义了忆阻器(Memristor)[2-3],称其为除电阻、电感和电容之外的第四种基本元器件。忆阻器的特性与生物神经突触有着惊人的相似之处,突触作为神经元之间的连接,可以通过动作电位改变其连接强度。忆阻器的电导类似于突触连接权值,可以通过控制流经忆阻器的电荷量或磁通量来修改其电阻。蔡教授提出的忆阻器为神经计算架构的实现提供了重要的基础元件。
为了模拟神经元动作电位的产生过程,建立“整合激发”型神经元SPICE仿真电路,对电路的脉冲产生过程进行了完整的仿真实验。之前已经有一些对神经元电路的研究文献存在[4-5],其中多是直接利用了忆阻器本身的特性,使用忆阻器交叉架构来连接多个神经元。但生物神经元之间的兴奋传递是单向的,仅使用单个忆阻器作为突触会造成突触后神经元产生的动作电位逆向影响突触前神经元,而非突触后神经元产生反馈抑制脉冲改变突触权值,这与实际生物神经元的特征不相符,根据这些问题重新设计了神经元突触电路结构[6]。可以实现在突触前后神经元不相互影响的前提下,完成突触前神经元对突触连接强度的强化以及突触后神经元对突触连接强度的抑制作用。并且此设计可使得突触电路在完成学习功能时更加符合Hebbian学习规则[7-9],因而更加符合生物神经系统特性。最后,完成了2个神经元之间的类似Hebbian学习的平均激发率学习,在基于多个神经元的基础上实现了Pavlov实验,证明了此电路结构在联想学习方面的可用性。
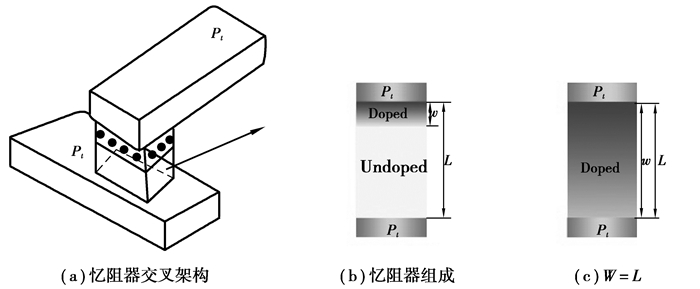
1 忆阻器模型在蔡少棠教授提出忆阻器的概念37年后,惠普实验室的Strukov等人在自然杂志上发表的论文中[3]提出了一种忆阻器的物理模型。他们将忆阻器的特征描述为等同于随时间变化的电阻,其电阻值在时间t时与通过自身的电荷量呈线性正比关系。这种忆阻器模型如图 1所示,在2条Pt纳米线的交叉点处夹杂着一层掺杂氧空位的二氧化钛(TiO2-x)和一层未掺杂氧空位的二氧化钛(TiO2)。其中掺杂氧空位的二氧化钛(TiO2-x)具有高电导,而纯二氧化钛(TiO2)具有绝缘性。两层二氧化钛的总电阻为忆阻器的阻值,称为忆阻(Memristance)。在忆阻器2端施加电压的情况下,忆阻器中会形成电场,氧空位会在电场的作用下从掺杂区向未掺杂区漂移,因此TiO2与TiO2-x之间的边界会发生迁移,忆阻器的电阻值会随之发生变化(如图 1所示)。
|
图 1 忆阻器模型 |
如图 1(b)所示,忆阻器可被看作2个电阻组成,分别为厚度为w的掺杂区和厚度为L-w的未掺杂区,其中L为2层二氧化钛的总厚度。忆阻器的电压和电流的对应关系的公式[7]如下
| $ u\left( t \right) = \left( {{R_{{\rm{ON}}}}\frac{{w\left( t \right)}}{L} + {R_{{\rm{OFF}}}}\left( {1 - \frac{{w\left( t \right)}}{L}} \right)} \right)i\left( t \right), $ | (1) |
其中RON和ROFF分别为掺杂层厚度最大和最小时忆阻器的极值电阻。w(t)为t时刻时掺杂区的厚度。其变化速度与通过忆阻器的电流之间的关系定义为
| $ \frac{{{\rm{d}}w\left( t \right)}}{{{\rm{d}}t}} = {u_v}\frac{{{R_{{\rm{ON}}}}}}{L}i\left( t \right), $ | (2) |
式中uv为平均离子迁移率,单位为cm2/(sV),对式(2)积分可得到w的计算公式
| $ w\left( t \right) = {u_v}\frac{{{R_{{\rm{ON}}}}}}{L}q\left( t \right) + {w_0}, $ | (3) |
w0为w的初始值,因为每类忆阻器厚度并不完全一致,引入一个标准化变量x(t)=w(t)/L (0<x<1),来表示w(t),新的表达式可以改写为
| $ \frac{{{\rm{d}}x\left( t \right)}}{{{\rm{d}}t}} = {u_v}\frac{{{R_{{\rm{ON}}}}}}{{{L^2}}}i\left( t \right), $ | (4) |
用M表示忆阻值,M(q)=d
| $ {M_0} = {R_{{\rm{ON}}}}\left( {x\left( {{t_0}} \right) + r\left( {1 - x\left( {{t_0}} \right)} \right)} \right), $ | (5) |
M0为在t0时刻的忆阻值,r为忆阻极值比率,r=ROFF/RON。忆阻在时间t时的计算公式如下
| $ M\left( q \right) = {M_0} - \Delta R\left( {\frac{{q\left( t \right)}}{{{Q_L}}}} \right), $ | (6) |
QL为使忆阻器掺杂层的厚度达到L时所需的总电荷量,因v(t)=M(q)·i(t),i(t)=dq(t)/dt,可得到电压的计算公式如下
| $ v\left( t \right) = \left( {{M_0} - \Delta R\left( {\frac{{q\left( t \right)}}{{{Q_L}}}} \right)} \right)\frac{{{\rm{d}}q\left( t \right)}}{{{\rm{d}}t}}, $ | (7) |
其中ΔR≈M0≈ROFF,因为d
| $ q\left( t \right) = {Q_L}\left( {1 - \sqrt {1 - \frac{2}{{{Q_L}{R_{{\rm{OFF}}}}}}\varphi \left( t \right)} } \right), $ | (8) |
又因为x(t)=x(t0)+q(t)/QL,假设初始状态时掺杂层厚度为0,则可得x的计算公式
| $ x\left( t \right) = 1 - \left( {\sqrt {1 - \frac{{2\varphi \left( t \right)}}{{r\beta }}} } \right), $ | (9) |
式中β=L2/uv。这种简单的线性离子漂移模型可以简化对忆阻器控制和其自身物理变化过程的理解。但实际上对于处在边界状态(x=0或x=1时)具有高速的离子漂移速度的情况来说,电场和离子漂移速率存在非线性关系。因此,这个函数是不能完全真实的模拟忆阻器边界状态的非线性特性。所以为更精确地描述忆阻器的特征,引入了1个窗口函数F(x, p),其中x是忆阻器的状态变量。公式(4)可以重新定义为
| $ \frac{{{\rm{d}}x\left( t \right)}}{{{\rm{d}}t}} = \frac{{{R_{{\rm{ON}}}}}}{\beta }i\left( t \right)F\left( {x\left( t \right), p} \right), $ | (10) |
其中窗口函数F(*)有多种选择,具体函数参考表 1。
| 表 1 窗口函数比较表 |
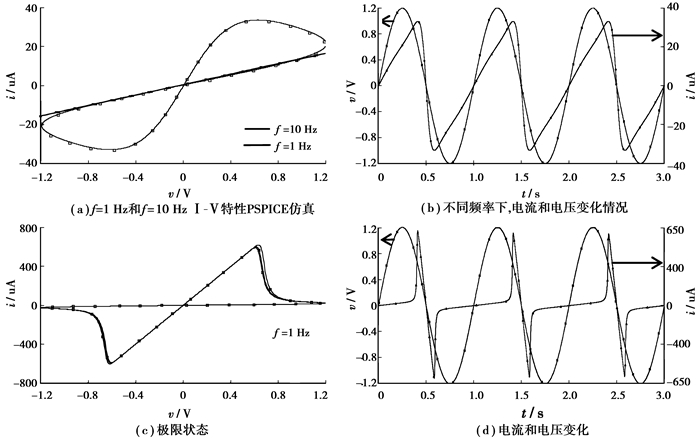
在简单的线性漂移模型下按照1.1中数学模型建立忆阻器SPICE模型[10-15]。图 2(a)中忆阻器在f=1 Hz的情况下的I-V特性PSPICE仿真结果。在低频时,可以明显的观察到磁滞回线,回线中各点处斜率的倒数即为忆阻值。而在高频状态下f=10 Hz,忆阻器的I-V特征曲线则趋向于一条y=ax的直线,此时忆阻器在短时间内的阻值不会发生较大变化,I-V特征曲线和固定电阻相似。图 2(b)显示了在0~3 s的时间内,忆阻器在两端施加频率为1 Hz大小为1.2 V的正弦电压时忆阻器的电压和电流变化情况。在加入窗口函数的非线性模型下,图 2(c)显示了忆阻器在f=1 Hz的情况下的I-V特性PSPICE仿真结果,“领结”的形状表现的更为明显,可以发现在电压在0.6~1.2 V阶段出现了明显的斜率变化,体现出在忆阻器的极限状态下的非线性特征。
|
图 2 忆阻器PSPICE仿真 |
使用Joglekar等人在文献[10]中提出的窗口函数
| $ f\left( x \right) = 1 - {\left( {2x - 1} \right)^{2p}}, $ | (11) |
其中p为控制参数,为正整数,x=w/L。f(x)其实可被看作一种边界控制函数,F(0)=F(1)=0,当p>3时,忆阻变化将趋向于线性,F(x)≈1(0<x<1)。
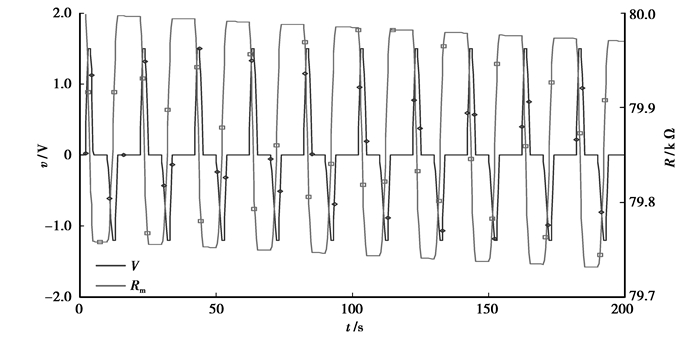
在以上的仿真实验过程中,在忆阻器两端施加正弦电压来观测阻值变化,需要模拟生物真实的动作电位作用于忆阻器来改变其自身阻值。生物神经动作电位基于神经细胞的“整合-激发(Integrate-And-Fire)”模型,因此动作电位表现为尖峰型脉冲的形式。在此基础上,分析脉冲对忆阻器的影响就十分重要。图 3所示为忆阻器两端施加脉冲电压时忆阻值的变化情况,类似于动作电位的强化和抑制作用。图中提供了200 ms内施加周期为20 ms宽度为2 ms大小为1.5 V的脉冲电压。在输出正向尖峰型脉冲时,忆阻器的阻值会出现近似于直线型下降,下降幅度可按照1.1节中公式(6)得出。在脉冲电压为零时,忆阻器会因为忆阻器自身的非易失性保持不变。所以忆阻器可以很好地实现相邻神经元之间突触基本学习功能[5]。
|
图 3 忆阻器脉冲影响仿真 |
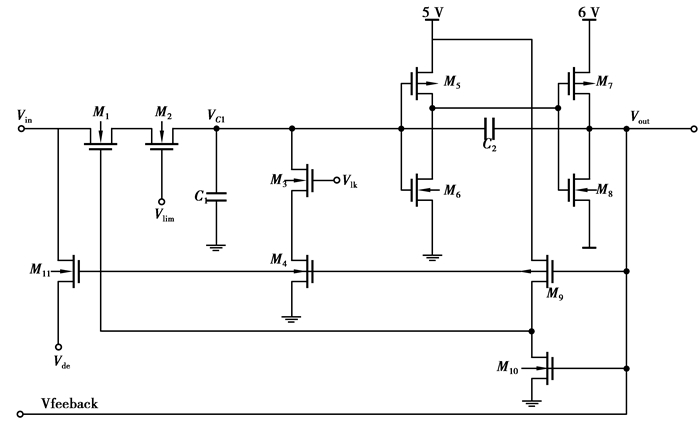
对人工神经元的认识应该从神经细胞模型开始,Mead在1989年出版的文献[11]提出了原始“整合激发(I&F)”神经细胞电路。后来Cantley等人对此电路进行了修改,在[12-14]中提出了神经细胞的新的电路模型,他们在电路中定义了一种新的MOS管模型,其具有纳米级特性,电信号是在理想的状态下设定,因此实现较为困难。如图 4所示,对其中电路进行了优化,并对电路参数进行了修改,使电路可产生较为真实合理的尖峰型脉冲动作电位。
|
图 4 改进型“整合激发”神经元电路 |
电路中M5、M7、M9为PMOS,其他为NMOS。已对电路中所有MOS管的SPICE模型参数进行修改,使MOS管的栅极导通电压阈值相同。相对于最初提出的神经元电路最大的优化在于增加了MOS管M11和Vde的控制电压,它弥补了原始电路只产生前馈脉冲,突触权重仅由突触前神经元控制的不足。Vde大小与忆阻的变化速度有直接关系。可设置在0.5~1 V之间,其值也可使用固定值。M11由输出脉冲Vout控制,在产生脉冲电压的同时,神经元电路会同时产生一个反向抑制脉冲,用于降低突触前后神经元的连接强度。电路中放置2个电容器C1、C2,C1充电需要一定时间,因此可控制Vc1电压变化慢于Vin,并且最高电压不会超过Vin,因此可作为定时器,电容充电计算公式如下
| $ V\left( t \right) = {V_0} + \left( {{V_{\rm{u}}} - {V_0}} \right)\left( {1 - \exp \left( { - \frac{t}{{RC}}} \right)} \right), $ | (12) |
其中V(t)为在t时刻电容C1两端的电压差,V0为初始时C1两端电压,Vu为充电完成后的极限电压,R为神经元电路中C1等效电路的总电阻,C为电容器C1电容值。
在不同的输入电压下,对电容的充电时间不同,所以Vc1达到M5和M6所组成反相器[13]阈值电压的时间就会不同,会使神经元产生脉冲间隔出现差别,即在具有较高输入电压时产生频率较高的脉冲,而在较低输入电压下产生低频率脉冲。因此电路中要选取大小合适的电容来控制脉冲的生成,如果在使用较小电容(C<10 uf)下电容充电速度随输入电压变化的特征将会变的不明显,使电容器失去定时的功能。而较大的电容(C>30 mf)则会需要较长的充电时间,在输入电压较小时达不到反相器的阈值电压。电路中C1的输入电流受到M1和M2的控制,其中M1受Vout的控制。M9为PMOS管,在输出端没有产生脉冲电压时(Vout≤0)处于导通状态,此时M1也将导通,相反在输出端产生脉冲电压时,M1则会阻断输入电流。而输入电压可在M2的控制下发生变化,MOS管的具体工作特性可参见文献[11]。在不同的Vlim的大小下可发生变化,对电容的充电速度进行控制。
电路中M3、M4组成漏电通路,用于电容器C1的放电。M4由脉冲信号控制,根据M3栅极电压Vlk的大小可控制C1放电速度。在产生脉冲电压时,Vout会大于M4的阈值电压,M4导通M9关闭,因此M1栅极电压为0 V。此时电容C1通过漏电通路放电,直到Vc1低于M5阈值电压,一个脉冲结束(M1导通,M4关闭)。以上为整个神经元电路产生一个脉冲电压的过程,在Vin不小于Vt(Vt为MOS管阈值电压)时,神经元会不断重复产生脉冲的过程。
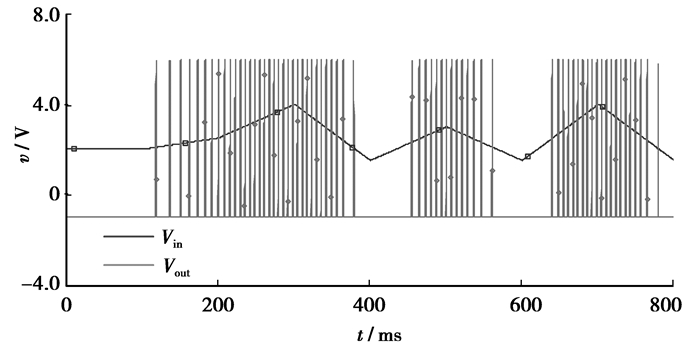
图 5给出了神经元电路输入电压与输出脉冲的PSPICE仿真图,仿真过程中在输入端使用了时长为800 ms的分段线性电源,每ms分别在2、2.5、4、1.5、3、1.5、4、1.5 V之间线性变化。从仿真结果中可以明显的观察到,在输入端电压较高时会输出频率更高的脉冲,反之在输入电压较低时,输出脉冲的频率也会相应降低。而在输入端电压小于MOS管阈值电压(2 V)时,不会产生脉冲。脉冲频率与输入端电压的大小有关,可按照公式(12)计算脉冲间隔时间从而得出输入电流/电压与脉冲频率的关系,按照所需脉冲频率给出对应的输入端电压值,用来塑造突触连接权值。
|
图 5 输入电压与输出脉冲关系PSPICE仿真结果 |
神经细胞之间需要通过突触连接,得知生物系统中神经元的相互连接特性主要表现在:
1) 生物神经系统中任意2个神经元都可以直接连接或发生连接关系,并且神经冲动能传送并接受到包括自身在内的众多神经元;
2) 生物神经元之间的连接效率不同并且可塑,因而其连接的作用或产生的连接效果不同。
因此在考虑神经系统电路设计中,要全面考虑电路的连接能力,并且突触要具有较高的可塑性,其连接效率要可根据神经元脉冲进行相应改变。为此Jo等人在文献[4]中提出了忆阻器交叉架构作为神经突触的设想,分析并描述了忆阻器自身特性与神经突触之间类似的特征,利用了忆阻器自身纳米级和非易失的特性,同时在设计突触电路时考虑神经网络学习规则的实现。虽然在连接性能上有了很大的提高,但仅使用单个忆阻器来做突触有个较大的局限性,其对时间要求严格,并且没有考虑神经元之间脉冲的逆向影响,不能真实地模拟生物突触的特性。因此重新构造了忆阻器突触的电路结构,使其更加符合生物神经系统的真实情况。
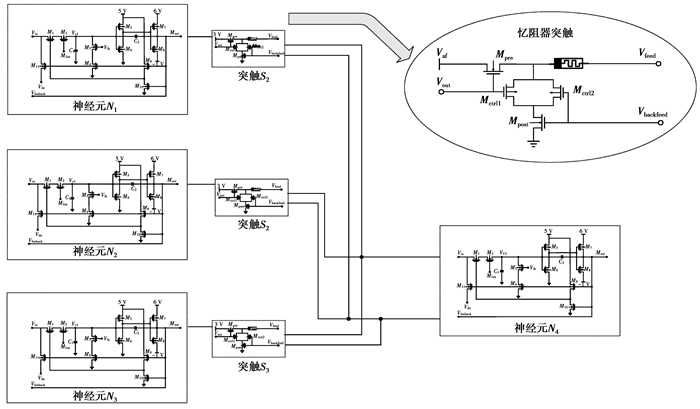
图 6中给出了4个神经元组成的简单神经网络结构,神经元之间由忆阻器突触连接。忆阻器突触电路由2个NMOS、2个PMOS与一个忆阻器组成,包括2个输入端和一个输出端。其中Mpre工作状态由突触前神经元的输出脉冲控制,Mpost则由突触后神经元的反馈脉冲电压控制。同时在突触后神经元产生的反向抑制脉冲的控制下对忆阻器阻值进行修改,对突触产生抑制作用。Mpre的源极电压由Vaf控制,大小可设置为高于抑制电压,在突触前后神经元同时产生脉冲时会增强突触连接权值。Vaf大小会影响到忆阻变化的快慢,可根据需求做出调整。仅使用Mpre与Mpost的突触电路结构在文献[5-12]中提出,但在只考虑单个脉冲且突触前后神经元在产生脉冲时刻完全一致时,Mpre与Mpost会同时导通使得突触前神经元脉冲输出端接地,此时忆阻器会由反向抑制脉冲控制,从而降低突触前后神经元连接强度,这不符合神经网络学习规则。为解决此问题增加了2个PMOS管Mctrl1与Mctrl2,使得Mpre与Mctrl1以及Mpost与Mctrl2各自构成反相器[13]。Mctrl1由突触前神经元输出端Vout控制,在突触前神经元产生脉冲时会使得Mctrl1栅极电压高于其阈值电压,此时Mctrl1会处于阻断状态。Mctrl2由突触后神经元的Vfeedback端控制,在突触后神经元产生脉冲时处于阻断状态。相反Mctrl1与Mctrl2都是会在突触前后神经元未产生脉冲时才会导通。因此在突触前后神经元脉冲频率相同且突触前后神经元产生脉冲时刻完全一致时会使漏电通路断开,所以在突触前神经元脉冲电压高于突触后神经元抑制电压的情况下会使脉冲作用于忆阻器,从而降低忆阻值,此时突触前后神经元的连接强度增强。而在突触前后神经元不同时产生脉冲时,Mctrl1与Mctrl2总会至少有一个处于导通状态,从而漏电通路是否导通要取决于Mpost的状态。在突触后神经元兴奋产生抑制电压时,会由后神经元的反馈端控制Mpost导通,从而抑制脉冲作用于忆阻器,增加忆阻值。此结构可很好地完成突触前后神经元产生脉冲时刻不同的多种情况下改变连接权值的功能。
|
图 6 4个神经元组成神经网络结构及忆阻器突触结构 |
联想学习[16-18]可以通过Pavlov实验[19]予以理解。生物神经系统与外界交互的过程是刺激反应的过程,学习的过程也是在刺激反映的中进行,Pavlov实验可以很好地体现这一特征。Pavlov实验是建立了狗关于食物和铃声的联想,实验初始狗看到或闻到食物会分泌唾液,而听到铃声却不会。在实验过程中,每次给狗食物的同时都向狗发出铃声,在实验结束时狗听到铃声腮腺便会分泌唾液。
在图 6中,给出了4个神经元组成的神经网络系统,可将N1视为狗视觉的传入神经元,N2为嗅觉传入神经元,N3为听觉传入神经元,N4为腮腺神经元。因为嗅觉与视觉对腮腺会产生同样的效果,所以可仅拿出N1和N4来分析学习规则,突触前神经元可直接产生脉冲影响突触后神经元。此学习规则建立在突触前后神经元的输出脉冲频率的基础上,在突触前神经元单独兴奋时,会对所有与之相连的突触产生影响,因此没有特异性。在突触后神经元产生兴奋而非此神经元兴奋引起时会对突触产生抑制脉冲,将突触的连接强度降低,因而在突触前神经元不兴奋而突触后神经元兴奋时会对突触产生抑制作用。而在突触前后神经元同时产生兴奋(脉冲频率相同且突触前后神经元脉冲时刻完全一致)时,此时突触前神经元脉冲高于后神经元兴奋产生的抑制脉冲,从而会使突触权重增大。相反突触后神经元输出脉冲频率高于突触前神经元时,必然不仅由突触前神经元单独引起,实际上是由与之相连的其他神经元输出脉冲共同刺激产生,此时突触后神经元抑制脉冲数必然大于突触前神经元的刺激脉冲数。在此过程中在突触前产生脉冲时会造成局部时刻忆阻降低,然而在总体上忆阻还是会呈现出增大的趋势。这类似于Hebbian学习,可称为平均激发率学习规则,基本规则如下:
1) 突触前神经元脉冲频率fpre大于等于突触后神经元脉冲频率fpost时,x(w/L)增大,忆阻器阻值M减小,前后神经元连接强度增强;
2) 突触前神经元脉冲频率fpre小于突触后神经元脉冲频率fpost时,x(w/L)减小,忆阻器阻值M增大,前后神经元连接强度降低。
3.2 神经系统电路SPICE仿真此神经系统电路学习规则将Hebbian学习的单一脉冲兴奋对突触权值的影响概括为在一定时间内神经元突触的平均激发率之差决定学习效果,具体学习规则效果可通过PSPICE的仿真实验观察,实验结果在图 7中给出。
|
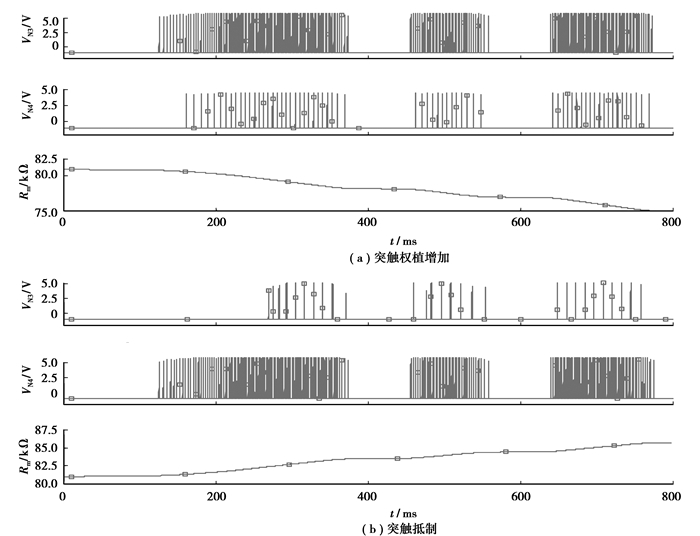
图 7 突触前后神经元脉冲频率与忆阻关系PSPICE仿真 |
图 7中给出了2个神经元在输出不同的脉冲电压时,对突触中忆阻器电阻的影响情况。初始状态时,N1与N4之间的连接效率较高,即N1与N4之间忆阻器阻值较低Rm1=100 Ω。N1产生的脉冲信号可直接引起N4兴奋,而N3与N4之间突触S3连接效率较低,阻值较高Rm3=80 kΩ,因此N3兴奋不可引起N4产生脉冲。
其中图 7(a)中突触前神经元N3的脉冲电压频率远大于突触后神经元N4脉冲频率,从而强化脉冲大于抑制脉冲,此时会使突触S3连接强度增强(x增大),在此表现为忆阻值降低。在突触后神经元产生了相应的兴奋,同时突触前神经元的脉冲频率较高时,认为突触后神经元的兴奋是由突触前神经元引起的。因此突触前后神经元同段时间内都处于兴奋状态,所以会造成突触权值的增加。图 7(b)给出的突触前神经元N3的输出脉冲频率小于突触后神经元N4,突触后神经元N4较高的脉冲频率时由其他与之相连的神经元刺激产生,此时的抑制脉冲数将会大于突触前神经元的强化脉冲数,使忆阻器突触S3的阻值增大(x减小),降低前后神经元之间的连接强度。此处为体现出更加明显的抑制效果,设置Vde大小为2 V。
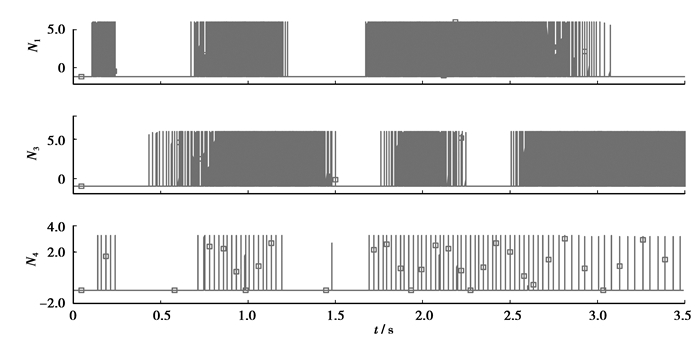
为证明此电路结构下联想学习的可行性,搭建了如图 6中的神经系统结构来实现完成Pavlov实验。图 8中提供了联想学习的PSPICE仿真结果,N1的脉冲由食物刺激产生,N3的脉冲由铃声刺激产生,N4脉冲是N1和N3的神经元刺激的结果。开始时在单独的N3刺激下不会产生任何脉冲,而在N1单独刺激下会产生脉冲。在N1、N3同时兴奋时,使得N3与N4也在同段时间内处于兴奋状态,因此N3与N4之间的连接强度将会增强。在经过足够长的时间后,N3与N4之间忆阻器阻值低于引起N4兴奋的阈值,此时N4可由N3单独引起兴奋,说明狗在听到铃声后会分泌唾液。仿真实验中在通过3.5s的学习后,可计算N3与N4之间的忆阻器阻值由降低到,这表明N3与N4之间的连接效率大幅提高,从而食物与铃声的联想学习得以实现。
|
图 8 Pavlov实验联想学习PSPICE仿真 |
通过对传统“整合激发”型神经元电路的修改,以及SPICE仿真电路的构造,产生了类似生物神经系统动作电位的脉冲信号。建立了忆阻器与MOS管结合的新型突触电路的结构,并利用2个神经元组成的神经网络实现了类似于Hebbian学习的神经网络学习规则,证明了此神经系统电路结构的可用性。在基于多神经元构成神经网络结构基础上实现了联想学习功能,在此过程中做了大量SPICE仿真实验。仿真结果表明,由忆阻器和MOS管组成的神经突触电路表现出类似生物神经突触的特性。忆阻器的纳米级特性增加了大量神经元相互连接的可能性,并且在只依赖于突触连接强度的前提下执行各种功能。文中提出的突触电路结构,可大大提高电路的集成度,增强了神经突触电路控制的精确性,为未来人工大脑的实现提供了可能。
| [1] | Pakkenberg B, Gundersen H J G. Neocortical neuron number in humans:effect of sex and age[J]. Journal of Comparative Neurology, 1997, 384(2): 312–320. DOI:10.1002/(ISSN)1096-9861 |
| [2] | Chua L. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507–519. DOI:10.1109/TCT.1971.1083337 |
| [3] | Chua L O, Kang S M. Memristive devices and systems[J]. Proceedings of the IEEE, 1976, 64(2): 209–223. DOI:10.1109/PROC.1976.10092 |
| [4] | Jo S H, Chang T, Ebong I, et al. Nanoscale memristor device as synapse in neuromorphic systems[J]. Nano letters, 2010, 10(4): 1297–1301. DOI:10.1021/nl904092h |
| [5] | Cantley K D, Subramaniam A, Stiegler H J, et al. Hebbian learning in spiking neural networks with nanocrystalline silicon TFTs and memristive synapses[J]. IEEE Transactions on Nanotechnology, 2011, 10(5): 1066–1073. DOI:10.1109/TNANO.2011.2105887 |
| [6] | Stafstrom C E, Schwindt P C, Crill W E. Repetitive firing in layer V neurons from cat neocortex in vitro[J]. Journal of neurophysiology, 1984, 52(2): 264–277. |
| [7] | Strukov D B, Snider G S, Stewart D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80–83. DOI:10.1038/nature06932 |
| [8] | Pershin Y V, Di Ventra M. Experimental demonstration of associative memory with memristive neural networks[J]. Neural Networks, 2010, 23(7): 881–886. DOI:10.1016/j.neunet.2010.05.001 |
| [9] | Hebb D O. The organization of behavior:A neuropsychological theory[M]. London: Psychology Press, 2002. |
| [10] | Joglekar Y N, Wolf S J. The elusive memristor:properties of basic electrical circuits[J]. European Journal of Physics, 2009, 30(4): 661. DOI:10.1088/0143-0807/30/4/001 |
| [11] | Mead C, Mohammed I. Analog VLSI implementation of neural systems[J]. Springer, 1989. |
| [12] | Cantley K D, Subramaniam A, Stiegler H J, et al. Neural learning circuits utilizing nano-crystalline silicon transistors and memristors[J]. Neural Networks and Learning Systems, IEEE Transactions on, 2012, 23(4): 565–573. DOI:10.1109/TNNLS.2012.2184801 |
| [13] | Subramaniam A, Cantley K D, Stiegler H J, et al. Submicron ambipolar nanocrystalline silicon thin-film transistors and inverters[J]. IEEE Transactions on Electron Devices, 2012, 59(2): 359–366. DOI:10.1109/TED.2011.2176737 |
| [14] | Cantley K D, Subramaniam A, Stiegler H J, et al.SPICE simulation of nanoscale non-crystalline silicon TFTs in spiking neuron circuits[C]//Circuits and Systems (MWSCAS), 201053rd IEEE International Midwest Symposium on IEEE, 2010:1202-1205. |
| [15] | Lehtonen E, Laiho M.CNN using memristors for neighborhood connections[C]//Cellular Nanoscale Networks and Their Applications (CNNA), 201012th International Workshop on IEEE, 2010:1-4. |
| [16] | Wey S T A. On SPICE macromodelling of TiO2 memristors[J]. Electronics Letters, 2009, 45(7): 377–379. DOI:10.1049/el.2009.3511 |
| [17] | Biolek Z, Biolek D, Biolkova V. SPICE model of memristor with nonlinear dopant drift[J]. Radioengineering, 2009, 18(2): 210–214. |
| [18] | Chen L, Li C, Wang X, et al. Associate learning and correcting in a memristive neural network[J]. Neural Computing and Applications, 2013: 1–6. |
| [19] | Pavlov I P, Thompson W H. The work of the digestive glands[M]. New York: Charles Griffin, 1902. |
| [20] | Principles of neural science[M].New York:McGraw-Hill, 2000. |
 2014, Vol. 37
2014, Vol. 37

