2. 重庆大学 计算机学院, 重庆 400044;
3. 美国哈佛大学 文理学院, 马萨诸塞州 02138
2. Department of Computer, Chongqing University, Chongqing 400044, China;
3. Department of Art and Science, Harvard University, MA 02138, USA
对中国水墨画进行计算机仿真是数字艺术领域最具挑战性的课题之一。水墨画是中国画的一种,它是中国人审美选择和认知的结果,包涵了中国传统文化精神,培养了中国人的审美意识和价值取向[1]。通过长期的演变和发展,形成了诸多风格派系,而且技法繁多,因为艺术创作过程中偶然因素和感性因素的大量存在,使得这种极为随意挥洒的艺术形式很难和逻辑严谨规范的计算机技术相融合。同时,计算机仿真涉及诸多的理论与技术,是多学科交叉的研究领域。因此,中国水墨画仿真研究,是传统水墨画艺术和现代计算机图形图像研究的交汇点,无论在科学技术还是在绘画艺术层面,都有着深远的意义和影响,对于计算机艺术和数字艺术的发展和实际应用都有积极的意义。
目前研究者就水墨画的计算机仿真方法进行了探讨,Strassmann[2]提出了生成水墨画效果的毛笔模型;Lee[3]等人提出了一个水墨与宣纸融合的模型,由于他们所提的纸结构都以像素矩阵为基础,提出的所有扩散算法也都是以像素为单位进行的,使得扩散区域十分规则,扩散效果不真实;Way[4]等人通过绘制纹理笔画来模拟中国山水画,提出了一种计算机生成水墨画岩石纹理的方法等。
笔者抽取体现中国水墨画特征的典型艺术效果,如浓淡,渗透,飞白等特效,对感性的艺术效果进行图像分析,为实现其数字化描述,建立了基于柏林噪声的中国水墨画仿真算法,经实验表明,所提方法实现的实时水墨动态特性能体现出水墨画的浓淡、渗透和飞白等艺术特征,能较好表现出水墨画水晕墨染的韵味。
1 柏林噪声 1.1 柏林噪声基本原理柏林噪声是由Berlin在八十年代提出的[5-8],它可以在某一空间生成连续的噪声。噪声函数是一系列随机噪音叠加起来而产生的一个连续函数,已被广泛应用于大理石、火焰云和云彩等效果的仿真模拟中。因此,很多人在程序中用随机数来创造不确定性,使得物体的运动、行为看起来更加自然或者生成各种各样的纹理图案。
根据不同的应用设计需求,柏林噪声可以在多维空间中实现各种功能设计的需求,以达到特定的渲染效果。柏林噪声可以在不同维度空间中,如一维、二维、三维,甚至四维空间中进行应用[9-11]。
例如:在一维空间中柏林噪声可以模拟生物的运动轨迹:有生命的对象很少长时间静止不动。在模拟手绘线条时,当用计算机绘制的线条时是笔直的,看起来不自然、不流畅,而把柏林噪声应用到一个摇摆画线算法中,则可使得用计算机绘制的线条更加像人工绘制的线条。同样,将柏林噪声函数应用在动画或者游戏中的人物身上,可以实时的调整一个虚拟人物的关节点的位置,使得虚拟人物看起来更加生动自然。而在二维空间中,二维柏林噪声函数可以较好的应用于山水画绘制渲染中。每一点的绘制都非常简单而逼真。色块的边界具有不规则性,而且能绘制出微小的细节,而这正好体现出自然界的物体具有多重变化级别的特性。绘制的属性也很容易手工设置,如对云朵的绘制,以及材质纹理的生成,用柏林噪声能够绘制出各种各样的材质效果,而且可以根据需要设定生成图像的大小,因而所产生的效果更加接近自然。在三维空间的运用中,可以用柏林噪声函数生成三维的云彩,当然,同时必须用到光线跟踪算法,这种方式不会产生像用二维纹理三维贴图方法时出现纹理扭曲变形的情况。在四维空间中的应用,例如,有动画效果的三维纹理和云彩,是把四维柏林噪声函数看作是随时间轴变化而变化的三维云彩或纹理。
因此,将柏林噪声理论应用于水墨画仿真中,把它用来模拟水墨画的典型艺术特征。可以通过构建柏林噪声函数来模拟绘制水墨的扩散渗透,浓淡,飞白等艺术效果。采用线性插值法和Cosine插值法的优点,而构建组合插值法来产生水墨画的艺术效果。
1.2 柏林噪声函数噪声函数从本质上来说就是一个随机数,但是它不像通常程序中用到的其他随机数,每次调用时都生成一个不同的随机数。这个噪声函数产生的随机数是由一个或多个参数计算生成的。当每次输入相同的参数时,它产生相同的返回值,而当输入的参数不同时,它产生的返回值是不同的随机数。
通过以上分析就清楚了需要怎样的随机数生成器,接下来就是去寻找产生这种随机数的函数。下面的代码就是一个能产生符合要求的函数,它的返回值是介于-0.1和1.0之间的浮点数。
function IntNoise(32-bit integer:x)
{ x=(x<<13)^ x;
return (1.0 -((x * (x * x * 15731+789221)+1376312589)& 7fffffff)/
1073741824.0);
}end IntNoise function
根据不同应用的需求,需要生成一个不同的随机数生成器。其实现步骤为:首先复制以上函数,然后改写相应的数字参数。这些大的数字参数都是质数,所以修改以后的数字也应该是质数。并且可以写出一个质数生成器的函数来完成这一功能需求。
通过多种噪声函数和插值方法,接下来创建一个柏林噪声函数。这个过程实际上是几个插值噪声函数的叠加。也就是说,柏林噪声只是一个函数,传递给它一个或多个参数,它返回一值。柏林噪声函数重要的部分是循环。每次循环迭代叠加另一个倍频,每次迭代调用一个不同的噪声函数。当然,并不需要真的写入倍频的噪声函数。所有的噪声函数实际上都是相同的,除了3个大质数不同以外,可以使用同样的代码,只是每个代码改用不同的质数。很多绘图应用程序就是运用二维噪声函数来生成山水的风景。如图 1所示即是在二维空间中创建不同频率的噪声函数所得到的不同效果。

|
图 1 不同频率的二维柏林噪声 |
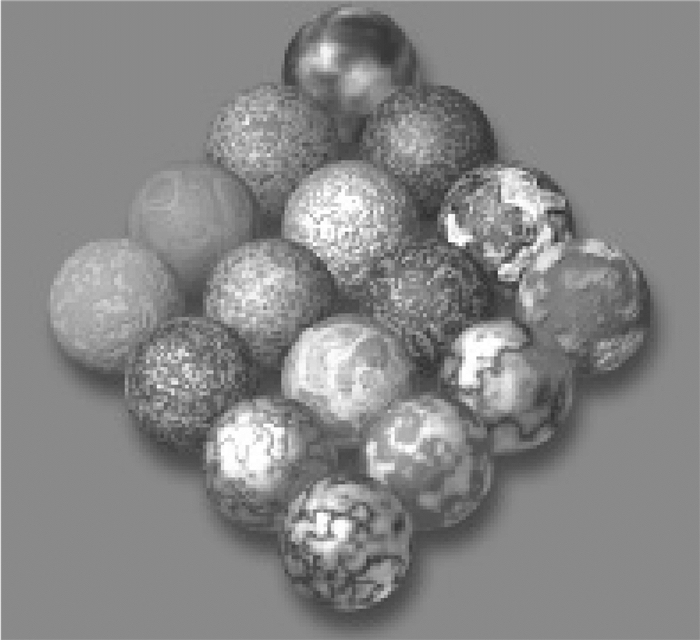
下面是将柏林噪声函数理论应用于实际应用中,并结合相应的模型来实现特定的应用。图 2则为运用不同柏林噪声后的球面效果。
|
图 2 运用不同柏林噪声后的球面效果图 |
水墨画的水墨主要是在纸的内部进行扩散和渗透的,因此水墨的运动不单单靠重力作用,更主要是纸纤维的吸水作用和墨粒子的粘附作用,进而产生扩散纹理[11-13]。而这些效果的显现除了与墨的浓度,即颜色的深浅有关之外,还与纸纤维的吸水性、用水量多少、用笔的角度力道以及纸纹理的情况有关,有时甚至完全是随机出现的效果,且水墨的形态是由不同变化层次的图案组合而成的。而这些特征表现出来的效果将它概括为水墨的浓淡,渗透,飞白等效果。
利用在一定范围内添加不同频率的噪声系数来实现一些特殊的水墨效果。在利用柏林噪声理论进行图形的渲染与绘制前,需构造柏林噪声函数和插值函数,并结合相应的模拟算法以综合实现图形绘制与渲染的效果。先将柏林噪声函数计算并存储为柏林噪声函数值分布表,为加快计算速度,不需每次对柏林噪声进行计算,只需一次性计算出所需已知范围内的分布。再在水墨模拟程序中加入柏林噪声函数,影响水墨的浓淡,渗透,飞白等效果。这种方法能够用于生成几乎所有的自然纹理,而且,它的输出能够容易地被应用到各种程序中。
在下述的方法中,先将柏林噪声函数通过计算和存储为柏林噪声函数值分布表。这是为了加快处理速度,不需每次对柏林噪声都进行计算,只需一次性就计算出所需已知值范围内的分布,形成一张一维函数数值映射表。以下图 3是水墨模拟的Cgfx的程序代码描述。Cgfx(是Nvidia公司提供的一种在图形处理器上编译运行的开发语言,主要为用户进行实时图形图像开发)

|
图 3 模拟的Cgfx的程序代码描述 |
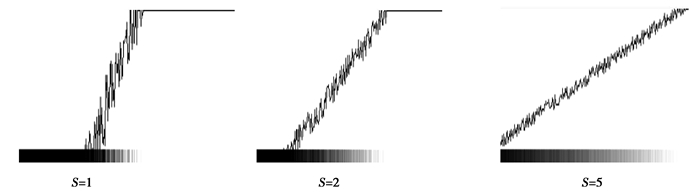
在进行了上述仿真程序后加入柏林噪声函数,使用物体表面的漫反射系数影响水墨画的浓淡,渗透,飞白等效果的线性分布。图 4为用不同等级参数所得到的函数预处理存储图。
|
图 4 线性插值生成函数 |
利用墨竹作为仿真的对象,根据三维竹模型为基础,和上述的柏林噪声原理结合起来,得到最终实现三维墨竹画的仿真效果。在仿真模拟中,去掉了书法、篆刻部分,仅仿真墨竹画的部分。同时手工绘制的墨竹画是在各类纸张如生宣、熟宣等材质上进行,经过一定的年限,纸张会有一定的颜色变化,如泛黄等。因此,将数字仿真墨竹画中添加一定的纸张所呈现出的背景色,以达到更好的中国水墨画仿真效果。
在仿真实验中通过构建多个柏林噪声函数来对墨竹画进行仿真绘制,验证了方法的可行性和有效性。而对各种效果的运用则是一个不同变化的动态叠加与融合过程。如通过GPU实现,则该方法可达到实时运算的速度。图 5所示,模拟出的墨竹画动态特征图,它体现出了墨色的变化及墨法的效果。所提方法可以实现实时水墨动态特性,能体现出墨竹画的浓淡、渗透和飞白等特征,能较好表现出水墨画水晕墨染的韵味。数字仿真墨竹画与手绘墨竹画有较高相似度,数字仿真墨竹画可信度较高。

|
图 5 计算机仿真模拟出的图像效果 |
因此基于柏林噪声的墨竹画的计算机仿真系统的技术开发基本上是成功的,实现了既定目标,具有较好的实验结果,并证明是可信的。
4 结语图像的计算机仿真生成,对自动水墨画效果处理,交互式作图以及虚拟作画等方面将有积极推动作用。对于丰富图形渲染领域的处理手段,推动计算机仿真技术的发展也将起到积极作用。鉴于传统中国水墨画自身的魅力以及计算机数字艺术的科学与艺术双重性,产生艺术效果的计算机仿真已经超出了科学仿真的一般意义,项目研究将无论在艺术还是在科学方面都有广阔的发展及应用前景,也能产生很好的经济、社会效益。
笔者采用面向艺术效果的仿真方法对水墨画进行仿真研究,将来的深入研究中,还可以从艺术角度分析中国水墨画的不同技法,并进行相应的算法改进,增加相应的特征变量及绘制参数等,以实现更好的水墨画仿真效果。同时也可以加入人机交互技术,人机交互的操作环境能给人带来身临其境的感受,使形态可根据需要进行实时地交互处理,以达到理想的构图效果。同时,本研究成果可推广到其他仿真研究中。通过研究和分析每种绘制风格的特征,从中提取特征信息,并建立相应的数学仿真模型来实现仿真绘制的效果。
| [1] | 杨维, 林健群. 中国美术史一古典美学思想与优秀作品赏析[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003. |
| [2] | Strassmann S.Hairy brushes[C]//Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH.Dallas:IEEE, 1986:225-232. |
| [3] | Lee J. Difusion rendering of black ink paintings using new paper and ink models[J]. Computers and Graphics, 2006, 25(2): 295–308. |
| [4] | Way D L, Shih Z C.The synthesis of rock textures in Chinese landscape painting[C]//Proceedings of Euro graphics'2001.Manchester:IEEE, 2007:123-131. |
| [5] | Paul B.Berlin Noise and Turbulence[M].http://paulbourke.net/texture_colour/perlin/2000. |
| [6] | Girshick A, Interrante V.Real-time principal direction line drawings of arbitrary 3D surfaces[C]//In SIGGRAPH'99 Conference Abstracts and Applications.1999. Los Angeles:IEEE, 1999:271. |
| [7] | Girshick A, Interrante V. Line direction matters:an argument for the use of principal directions in 3D line drawings[J]. Symposium on Non-Photo realistic Animation and Rendering, 2000: 43–52. |
| [8] | Hertzmann A, Perlin K.Painterly rendering for video and interaction[C]//In Proceedings of NPAR 2000, ACM SIGGRAPH.Anneci:IEEE, 2000, 12(6):7-12. |
| [9] | Zhang Q, Sato Y, Takahashi J. Simple cellular automaton-based simulation of ink behavior and its application to suibokugalike 3d rendering of trees[J]. The Journal of Visualization and Computer Animation, 1999, 10: 27–37, 1999. DOI:10.1002/(ISSN)1099-1778 |
| [10] | Winkenbach G, Salesin D H.Rendering parametric surfaces in pen and ink[C]//Proc.Siggraph 96.ACM Press, 2006.p:469-476. |
| [11] | Lake A, Marshall C, Harres M. real-time 3D animation[J]. Stylized rendering techniques for scalable and Salesin, 2012: p:13–20. |
| [12] | Hertzmann A.Fast paint texture[C]//In NPAR 2002:2nd In Symposium on Non-photorealistic Animation and Rendering.Annecy France:IEEE, 2002:91-96. |
| [13] |
周党培, 陈业仙.
牛顿环实验的计算机仿真[J]. 四川兵工学报, 2009(7): 139–141.
ZHOU Dangpei, CHEN Yexian. Computer simulation of Newton rings experiment[J]. Journal of Sichuan Ordnance, 2009(7): 139–141. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


