应用于切割等场合的压紧机构,由于压紧力与工件对压板的反作用力不共线,存在一定的偏心距,再加上压紧时工件对压板的侧向推力,使得压板产生较大的倾翻力矩,作用到导向轴上就会产生弯曲变形等强度问题,从而严重影响压紧机构的使用性能和寿命。因此,在满足强度刚度的条件下对导向轴的结构尺寸进行优化设计就显得非常重要。
随着计算机技术的迅速发展,有限元方法在工程中得到了广泛的应用。文献[1]应用有限元中的稳态热分析对轴承系统进行了整体热弹流性能分析;文献[2]应用有限元中的形状优化对传统三梁四柱式液压机下横梁进行结构拓扑优化;文献[3]应用有限元中的预应力模态分析对直线滚动导轨系统进行了整体建模分析;文献[4]采用有限元软件ANSYS的参数化编程语言APDL对汽车磁流变阻尼器的结构参数进行了优化;文献[5-6]对大型回转窑液压挡轮装置中的导向轴进行了受力分析与设计;文献[7]对冷却机液压挡轮装置中的导向轴进行了有限元接触分析;文献[8]对水下绳锯机张力检测装置中的导向轴进行了形状优化设计。然而,导向轴的研究还有许多问题有待解决。例如,现有导向轴的研究还没有进行底座―导向轴―上梁的整体静力学性能分析,以更真实地反映导向轴系统的性能;在较大的径向载荷下,显著的轴向弯曲变形可能会发生;竖直工位的导向轴不需要考虑自重的影响,也无需考虑轴上运动部件重力的影响。而现有的导向轴研究,大都集中在水平工位导向轴承受自重和轴上运动部件重力的单独原件静力分析上。
针对上述问题,笔者通过把底座―导向轴―上梁作为一个整体,来研究竖直工位导向轴系统的静力学特性。这种方法的优点是,把导向轴与底座和上梁联接处的未知力边界条件转化为系统内部边界条件,避免了过多人为假设条件的引入,使得数值计算和有限元分析结果更接近于导向轴系统真实工况下的特性。
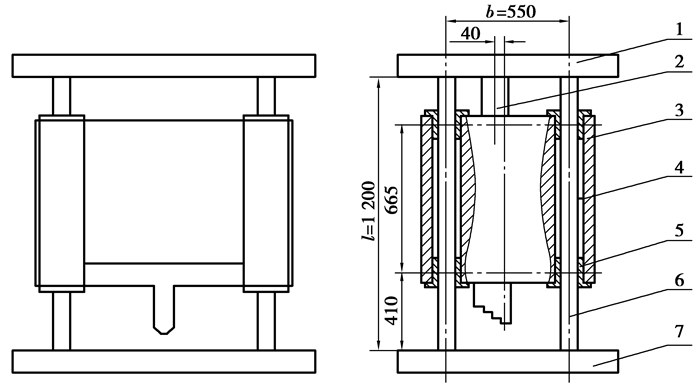
1 机械结构由图 1可见,压紧机构主要由五部分组成,底座固定,导向轴和上梁通过螺栓连接,存在一定的变形协调关系。压板通过滑套和石墨轴套与导向轴连接,可在导向轴上上下滑动,由于石墨轴套的润滑作用,可忽略压板上下运动的摩擦力。压紧轴的工作压力由油缸提供,单缸工作压力为12.5 t。压紧轴的轴心线与压板所受的反作用力存在一定的偏心距,同时压板还受到工件对其的侧向推力FT(如图 2(a)所示),故而会产生倾翻力矩,作用到导向轴上就会有横力,而横力将使导向轴产生弯矩,从而产生横力弯曲变形。
|
图 1 压紧机构结构图 1—上梁;2—压紧轴;3—压板;4—石墨轴套;5—滑套;6—导向轴;7—底座 |
|
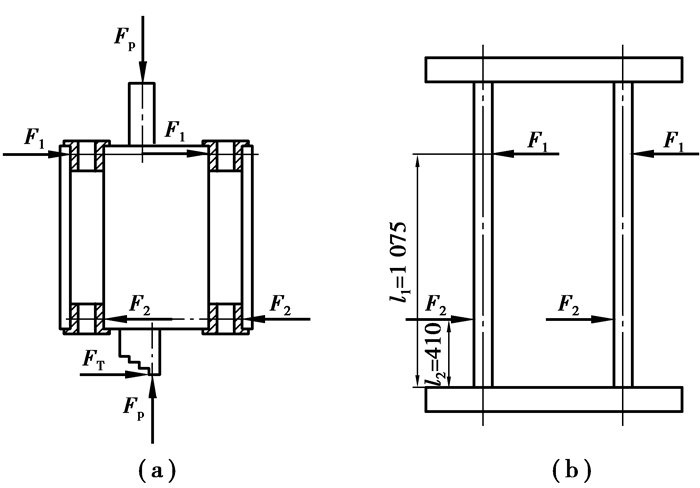
图 2 压板和导向轴受力图 Fp—压紧力;F1—导向轴对上滑套的集中力;F2—导向轴对下滑套的集中力;FT—工件对压板的侧向推力 |
压紧机构的工作环境为强辐射、强腐蚀性,这就要求其零件材料具备高强度和耐蚀性,所以选择马氏体不锈钢(1Cr17Ni2)作为压紧机构所有零部件的材料。
在设计中如何保证这一压紧机构导向轴的强度和刚度满足要求,就成了设计工作的难点和重点。为此采用力法对压紧机构导向轴进行结构尺寸设计,同时利用三维接触有限元软件对此压紧机构导向轴进行强度校核。
2 圆形截面轴的强度校核方法根据文献[9]可知,塑性材料的极限应力为屈服极限,脆性材料的极限应力为强度极限。由于设计选用的材料为1Cr17Ni2,属于塑性材料,故而其许用应力的计算公式为
| $ \left[\sigma \right] = \frac{{{\sigma _{0.2}}}}{{{n_{\rm{s}}}}}, $ | (1) |
式中:σ0.2是材料的屈服极限,1Cr17Ni2的屈服极限为770 MPa;ns为材料的安全系数,取ns=4.5。
根据文献[10]可知,截面为圆形的杆件,其弯曲强度校核公式为
| $ {\sigma _{\max }} = \frac{{{M_{\max }}}}{{{W_z}}} = \frac{{32{M_{\max }}}}{{{\rm{ \mathit{ π} }}{D_3}}} \le \left[\sigma \right], $ | (2) |
式中:Mmax为杆件所受最大弯矩;D是杆件截面直径;Wz是抗弯截面系数。对于圆形截面,
根据文献[11, 14]可知,在线性变形条件下一次超静定结构的力法方程为
| $ {\delta _{11}}{X_1} + {\mathit{\Delta} _{1{\rm{p}}}} = 0, $ | (3) |
式中Δ1p为基本结构在荷载单独作用下沿X1方向的位移;δ11为比例系数。在数值上等于基本结构在单位力X1=1单独作用下沿X1方向产生的位移;X1是未知力。
3.2 模型的建立压板受力图如图 2(a)所示。计算时,假设上梁和底座均为刚体,则可将上梁、导向轴和底座作为一个整体来进行分析,且由于载荷为平面对称加载,因此取一半化为平面问题进行分析。导向轴受力图如图 2(b)所示。
3.3 边界条件的确定边界条件需根据压紧机构的不同工作状态进行确定,为了校验压紧机构导向轴的强度需选择其中最恶劣的工况进行分析,即压紧机构处于满载工况,两个压紧轴同时工作,每轴工作压力为12.5 t,且工件对压板的侧向推力为3.75 t(根据文献[12]可知,有压板剪切时,侧向推力T≈(0.1~0.18)P,此处取T=0.15P),此时导向轴与滑套接触部分承受工作压力,该压力均匀分布于高为120 mm的圆柱面上(滑套高为120 mm),为方便计算,可简化为集中力计算。
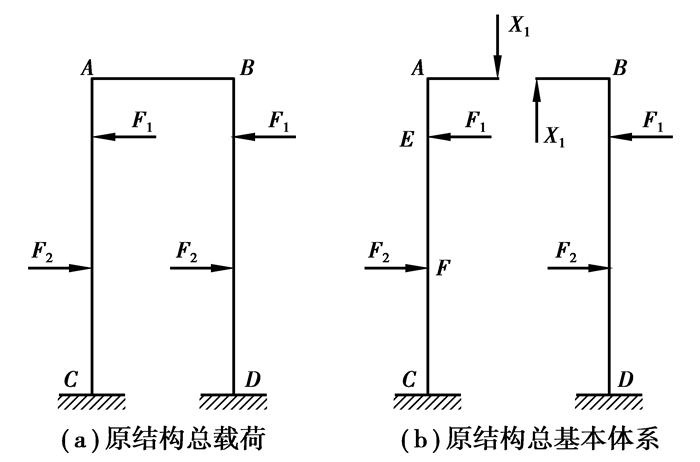
3.4 导向轴结构尺寸设计将上梁、导向轴和底座作为一个整体框架进行计算,则图 3(a)示结构为1次超静定结构。在反对称载荷的作用下,基本体系如图 3(b)所示。切口截面的弯矩、轴力都是对称未知力,应为零;只有反对称未知力X1存在。
|
图 3 结构受力模型 |
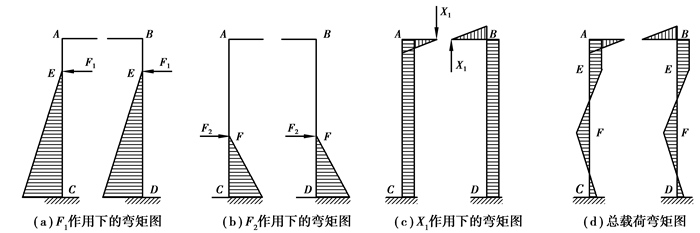
基本结构在荷载和单位未知力作用下的弯矩图如图 4(a)(b)(c)所示。由此得
|
图 4 弯矩图 |
| $ {\mathit{\Delta} _{1{\rm{p}}}} = {\mathit{\Delta} _{1{F_1}}} + {\mathit{\Delta} _{1{F_2}}}, $ | (4) |
| $ {\mathit{\Delta} _{1{F_1}}} = \frac{1}{{EI}}\int_0^{{l_1}} {{F_1} * x * \frac{b}{2}{\rm{d}}x} = - \frac{{{F_1}bl_1^2}}{{4EI}}, $ | (5) |
| $ {\mathit{\Delta} _{1{F_2}}} = \frac{1}{{EI}}\int_0^{{l_2}} {{F_2} * x * \frac{b}{2}{\rm{d}}x} = \frac{{{F_2}bl_2^2}}{{4EI}}, $ | (6) |
| $ {\delta _{11}} = \frac{1}{{EI}}\int_0^l {{{\left( {\frac{b}{2}} \right)}^2}{\rm{d}}x} + \frac{1}{{E{I_2}}}\int_0^{\frac{b}{2}} {{x^2}{\rm{d}}x} = \frac{{{b^2}l}}{{4EI}} + \frac{{{b^3}}}{{24E{I_2}}}, $ | (7) |
带入力法方程式(3),得
| $ {X_1} = - \frac{{{\mathit{\Delta} _{1{\rm{p}}}}}}{{{\delta _{11}}}} = - \left( {\frac{{{\mathit{\Delta} _{1{F_1}}} + {\mathit{\Delta} _{1{F_2}}}}}{{{\delta _{11}}}}} \right) = \frac{{6\left( {{F_1}l_1^2 - {F_2}l_2^2} \right)}}{{6bl + {b^2}\frac{{EI}}{{E{I_2}}}}}。$ | (8) |
令
| $ {X_1} = \frac{{{F_1}l_1^2 - {F_2}l_2^2}}{{bl}}。$ | (9) |
将已知数据代入文献[10]中的弯矩公式,可得钢架的总载荷弯矩图如图 4(d)所示。
根据总载荷弯矩图,求出最大弯矩,代入强度校核公式(2)可得
| $ {D_{\min }} \ge \sqrt[^3]{{\frac{{32{M_{\max }}}}{{{\rm{ \mathit{ π} }}\left[\sigma \right]}}}}。$ | (10) |
至此,可得出导向轴结构尺寸的设计计算步骤为:1)利用文献[13]中的力平衡和力矩平衡公式求出导向轴上的集中力F1和F2;2)由式(9)计算出反对称未知力X1,然后做出体系的弯矩图确定最大弯矩Mmax;3)由式(10)计算导向轴的最小截面直径Dmin。
3.5 计算结果根据推导出的参数及公式,输入表 1中的已知参数,可求出表 2中的相关参数。
| 表 1 已知参数表 |
| 表 2 力法输出参数表 |
根据文献[11, 14]可知,等截面杆件AB在一端具有不同支座时的刚度方程如下。
1) B端为固定支座。
| $ {M_{AB}} = 4i{\theta _A} - 6i\frac{\mathit{\Delta} }{l}, $ | (11) |
| $ {M_{BA}} = 2i{\theta _A} - 6i\frac{\mathit{\Delta} }{l}。$ | (12) |
2) B端为铰支座。
| $ {M_{AB}} = 3i{\theta _A} - 3i\frac{\mathit{\Delta} }{l}, $ | (13) |
| $ {M_{BA}} = 0。$ |
式中:MAB,MBA为杆端弯矩;θA为结点A的转角;Δ为杆AB两端垂直于杆轴的相对位移;l为杆长。
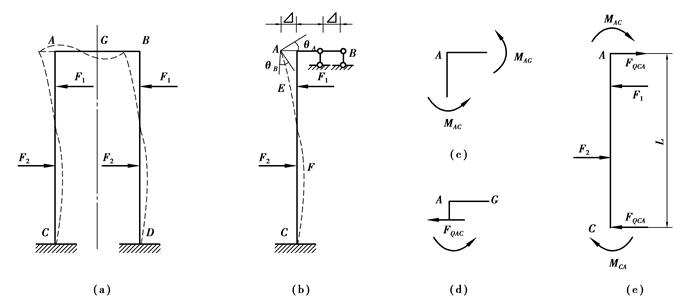
4.2 导向轴结构尺寸设计模型及边界条件与力法相同。作用于对称结构上的任意荷载,可以分为对称荷载和反对称荷载两部分分别计算。在对称荷载的作用下,变形是对称的,弯矩图和轴力图是对称的,而剪力图是反对称的。在反对称荷载的作用下,变形是反对称的,弯矩图和轴力图是反对称的,而剪力图是对称的。利用这些规则,计算对称刚架时,只需计算这些结构的半边结构。如图 5(a)示奇数跨对称结构中,在对称轴的截面G没有竖向位移,但可有水平位移和转角。计算中所取的半边结构如图 5(b)所示,G端为辊轴支座。
|
图 5 结构受力模型 |
图 5(a)示钢架,导向轴的线刚度为i1,上梁的线刚度为i2,基本未知量为刚结点A的转角θA和轴顶的水平位移Δ,如图 5(b)示。由于杆CA的两端结点有相对侧移Δ,但杆AG的两端结点只有整体的水平位移,而没有相对的垂直位移。利用等截面杆件的刚度方程,并叠加固端弯矩后,可列出各杆的杆端弯矩如下:
| $ {M_{CA}} = 2{i_1}{\theta _A} - 6{i_1}\frac{\mathit{\Delta} }{l} - \frac{{{F_2}{l_2}b_2^2}}{{{l^2}}} + \frac{{{F_1}{l_1}b_1^2}}{{{l^2}}}, $ | (14) |
| $ {M_{AC}} = 4{i_1}{\theta _A} - 6{i_1}\frac{\mathit{\Delta} }{l} + \frac{{{F_2}l_2^2{b_2}}}{{{l^2}}} - \frac{{{F_1}l_1^2{b_1}}}{{{l^2}}}, $ | (15) |
| $ {M_{AG}} = 3{i_2}{\theta _A}。$ | (16) |
建立基本方程,首先,与结点A的角位移θA对应,取结点A为隔离体(图 5(c)),可列出力矩平衡方程:
| $ \sum {{M_A} = 0, } $ |
| $ \begin{array}{*{20}{c}} {{M_{AC}} + {M_{AG}} = 0, }\\ {4{i_1}{\theta _A} + 3{i_2}{\theta _A} - 6{i_1}\frac{\mathit{\Delta} }{l} + \frac{{{F_2}l_2^2{b_2}}}{{{l^2}}} - \frac{{{F_1}l_1^2{b_1}}}{{{l^2}}} = 0。} \end{array} $ | (17) |
其次,与横梁水平位移Δ对应,取上梁AG部分为隔离体(图 5(d)),可列出水平投影方程:
| $ \begin{array}{l} \sum {{F_x} = 0, } \\ {F_{QAC}} = 0。\end{array} $ | (18) |
式(18)中的杆端剪力可以换成杆端弯矩。为此,取轴CA作隔离体(图 5(e)),得
| $ \begin{array}{*{20}{c}} {\sum {{M_C} = 0, } }\\ {{M_{AC}} + {M_{CA}} + {F_{QAC}}l + {F_2}{l_2} - {F_1}{l_1} = 0, }\\ {{F_{QAC}} = - \frac{1}{l}\left( {{M_{AC}} + {M_{CA}} + {F_2}{l_2} - {F_1}{l_1}} \right)。} \end{array} $ | (19) |
将剪力表达式(19)代入式(18),得
| $ {M_{AC}} + {M_{CA}} + {F_2}{l_2} - {F_1}{l_1} = 0。$ |
再利用式(14)、(15),得
| $ 6{i_1}{\theta _A} - 12{i_1}\frac{\mathit{\Delta} }{l} + \frac{{{F_2}{l_2}{l_2}}}{{{l^2}}}\left( {{l_2} - {b_2}} \right) - \frac{{{F_1}{l_1}{b_1}}}{{{l^2}}}\left( {{l_1} - {b_1}} \right) + {F_2}{l_2} - {F_1}{l_1} = 0。$ | (20) |
解联立方程(17)(20),就可求出结点位移Δ和转角θA,然后代入式(14)(15)(16),可求出杆端弯矩,从而作出刚架弯矩图(见图 4)。
4.3 计算结果根据推导出的参数及公式,输入表 1中的已知参数,可求出表 3中的相关参数。
| 表 3 位移法输出参数表 |
采用通用有限元软件Abaqus,直接创建导向轴的三维实体模型,导向轴、底座以及上梁合并为一体。建立了导向轴承受满载工况时的受力仿真分析模型,分析计算了导向轴在承受一定弯矩时的变形量和应力分布,使设计人员在设计的时候就能准确了解到构件每部分的应力、应变及位移,以便更好地对结构进行反复的修改,达到优化的目的。本次设计选用材料为1Cr17Ni2马氏体不锈钢,其力学性能如表 4所示。
| 表 4 马氏体不锈钢力学性能 |
对于此次设计的压紧机构导向轴,为了提高计算精度,采用8节点6面体网格,并在4根导向轴的径向和轴向适当加密,划分的网格如图 6所示。

|
图 6 导向轴有限元网格模型 |
要实现对该导向轴的力学有限元分析,主要是合理确定载荷大小和约束条件。对于该导向轴,其满载工况较为简单,载荷为沿y轴正向的F1=7 483.55 N和沿y轴负向的F2=16 671.05 N的两个集中力,加载集中力的区域为指定位置处的一个半圆周,载荷的施加位置如图 2(b)所示,约束边界条件为底座固定,即底座底面建立全约束。
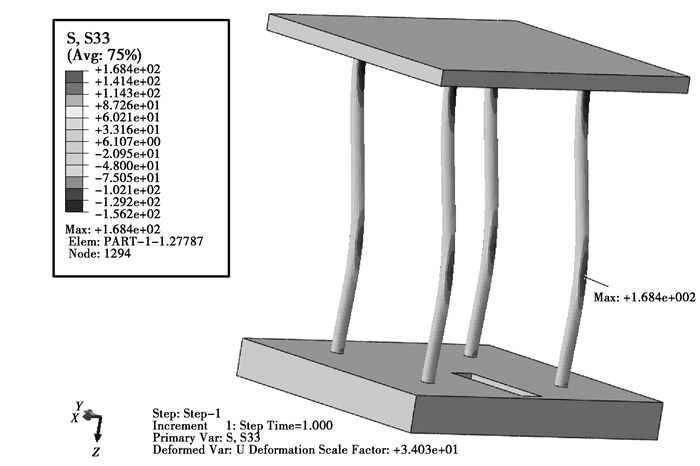
5.3 计算结果分析本次导向轴的结构尺寸设计中,主要关心的是导向轴的轴向弯曲应力分布及其最大值。压紧机构导向轴的轴向应力云纹图,如图 7所示。
|
图 7 满载时导向轴的轴向弯曲应力 |
由图 7可以看出导向轴承受的轴向弯曲应力的最大值为168.4 MPa,接近并且小于设计时使用的许用弯曲应力值171.1 MPa,且最大弯曲应力出现在集中力F2施加的位置,这与计算所得的最大弯矩出现的位置一致(见图 4(d)),这说明结构设计是合理的。图 8清楚地显示了导向轴最大应力截面上的应力分布。

|
图 8 最大应力截面应力分布图 |
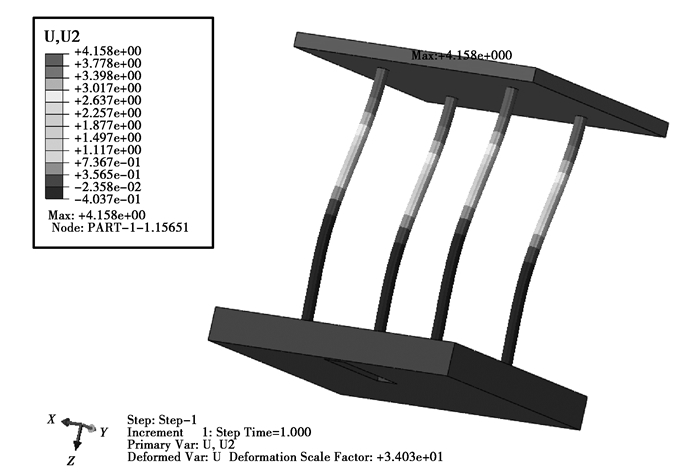
由图 9可知在满载工况时导向轴的最大变形量为4.158 mm,接近并且小于位移法所计算出的数值4.516 mm,最大变形位于导向轴上端与上梁连接的区域,其变形的大小相对于导向轴的截面尺寸较小,符合设计要求。
|
图 9 满载时导向轴上的变形 |
笔者针对特殊场合的压紧机构,压紧力与工件对压板的反作用力不共线,且压紧时存在工件对压板的侧向推力产生的倾翻力矩,使得导向轴产生弯曲变形等强度问题,从而严重影响压紧机构的使用性能和寿命的情况,对导向轴的截面尺寸进行研究,研究结果可为相似情况提供参考价值,且本结构已成功应用到某特殊环境的压紧机构中。
通过对压紧机构导向轴的结构尺寸设计及强度分析研究,可以得到以下结论:
1) 压紧机构在满载工况时,导向轴所受到轴向弯曲应力最大值小于许用应力,满足设计条件。
2) 压紧机构在满载工况时,导向轴的轴向变形位移相对于导向轴的尺寸较小,符合设计要求。
3) 所推导出的在对称载荷作用下的一次超静定结构的设计参数和公式同样适用于其他类似结构。
| [1] |
孟凡明.
水润滑轴承系统三维热弹流性能有限元分析[J]. 重庆大学学报, 2013, 36(2): 121–126.
MENG Fanming. Three-dimensional finite element analysis for thermo-elasto-hydrodynamic performances for a water lubricated bearing system[J]. Journal of Chongqing University, 2013, 36(2): 121–126. DOI:10.11835/j.issn.1005-2909.2013.02.031 (in Chinese) |
| [2] |
张大可, 孙圣权.
液压机下横梁结构拓扑的进化结构优化[J]. 重庆大学学报, 2009, 32(10): 1117–1121.
ZHANG Dake, SUN Shengquan. Evolutionary topology optimization of the lower stable of a hydraulic press[J]. Journal of Chongqing University, 2009, 32(10): 1117–1121. DOI:10.11835/j.issn.1000-582X.2009.10.001 (in Chinese) |
| [3] |
孙伟, 孔祥希, 汪博, 等.
直线滚动导轨动力学精细有限元建模[J]. 重庆大学学报, 2013, 36(3): 37–41.
SUN Wei, KONG Xiangxi, WANG Bo, et al. A precise finite element modeling approach for analyzing linear rolling guidewaydynamics[J]. Journal of Chongqing University, 2013, 36(3): 37–41. DOI:10.11835/j.issn.1005-2909.2013.03.010 (in Chinese) |
| [4] |
李以农, 潘杰锋, 郑玲.
磁流变阻尼器的有限元参数优化设计[J]. 重庆大学学报, 2010, 33(5): 35–40.
LI Yinong, PAN Jiefeng, ZHENG Ling. Design optimization of magneto-rheological damper based on finite element parametric language[J]. Journal of Chongqing University, 2010, 33(5): 35–40. DOI:10.11835/j.issn.1674-4764.2010.05.007 (in Chinese) |
| [5] |
赵海波.
回转窑液压挡轮装置导向轴的计算分析[J]. 有色设备, 2012(6): 15–19.
ZHAO Haibo. The Computational analysis for the lead stalk of rotarykiln hydraulic block wheel device[J]. Non-ferrous Metallurgical Equipment, 2012(6): 15–19. (in Chinese) |
| [6] |
李英.
大型回转窑液压挡轮轴的设计[J]. 有色设备, 2012(4): 45–47.
LI Ying. Hydraulic blocking wheel shaft of large scale rotary kiln design[J]. Non-ferrous Metallurgical Equipment, 2012(4): 45–47. (in Chinese) |
| [7] |
吴迪, 万会雄, 邹哲维, 等.
冷却机液压挡轮装置中关键部件的有限元分析[J]. 武汉理工大学学报:交通科学与工程版, 2008, 32(5): 956–958.
WU Di, WAN Huixiong, ZOU Zhewei, et al. Finite element analysis of the key package in hydraulic blocking-wheel of cooling machine[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2008, 32(5): 956–958. (in Chinese) |
| [8] |
王海波, 孟庆鑫, 邵泽波, 等.
水下绳锯机张力检测装置的设计[J]. 吉林化工学院学报, 2008, 25(1): 63–65.
WANG Haibo, MENG Qingxin, SHAO Zebo, et al. Design of the tensile detecting devioe for the underwater wire saw[J]. Journal of Jilin Institute of Chemical Technology, 2008, 25(1): 63–65. (in Chinese) |
| [9] | 李良军. 机械设计[M]. 北京: 高等教育出版社, 2010. |
| [10] | 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2004. |
| [11] | 龙驭球, 包世华. 结构力学[M]. 北京: 高等教育出版社, 2000: 315-469. |
| [12] | 邹家祥. 轧钢机械[M]. 3版. 北京: 冶金工业出版社, 2000. |
| [13] | 哈尔滨工业大学理论力学教研室. 理论力学[M]. 北京: 高等教育出版社, 2002. |
| [14] |
刘学军.
力法、位移法、无剪力分配法等在结构计算中的选用[J]. 吉林建筑工程学院学报, 2006, 23(2): 34–36.
LIU Xuejun. The selection of mechanical means, displacement means and no shear force distribution means[J]. Journal of Jilin Architectural and Civil Engineering Institute, 2006, 23(2): 34–36. (in Chinese) |
| [15] | 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006. |
| [16] |
王勇勤, 林秉敬, 严兴春, 等.
165MN自由锻造油压机组合梁强度分析研究[J]. 机械设计与制造, 2009, 5(5): 178–180.
WANG Yongqin, LIN Bingjing, YAN Xingchun, et al. The strength analysis of the composite beam of the 165MN free forging hydraulic press machine[J]. Mechinery Design and Manufacture, 2009, 5(5): 178–180. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

