b. 同济大学 建筑设计研究院, 上海 200092
b. Tongji Architectural Design (Group)Co., Ltd., Tongji University, Shanghai 200092, China
冰浆是冰晶与水的混合物,冰浆的融解热大,相同温差下,冰浆用做载冷剂将会携带更多的冷量,国外的空调系统中已有把冰浆作为载冷剂的工程实例[1-2]。
地铁站空调系统多采用单站供冷模式,但在城市中心区存在冷却塔的噪音与瓢水问题,且单站供冷机房管理维护较集中设置冷站复杂,因此部分城市采用集中设置冷站提供多个地铁站空调系统所需冷源,但集中冷站系统二次管网的能耗巨大,为解决集中供冷输配系统能耗大的问题,国外(日本、韩国等)已有采用冰浆作为载冷剂输配冷量。
文中依据冰浆在暖通空调领域的最新研究成果,分析了主要气候区代表城市(北京、上海、广州)多地铁站集中供冷分别采用冰浆及低温冷冻水(冰蓄冷系统)作为载冷剂的二次管网的单位长度年度费用值(单位长度年度费用值为最优保温层厚度及管道内径下的优化值,计算分析所用冰浆假设为纯水制取,末端空调负荷变化时保持冰浆的含冰率不变,改变冰浆流量)。以此为依据分析冰浆集中供冷系统的适用性。
1 二次管网年度费用 1.1 冰浆压降计算方法国内外学者对冰浆的压降计算进行了试验研究[3-4],文中计算参照文献[4]给出的试验公式,当量摩擦阻力系数参照文献[5]给出的修正。
1) 沿程阻力的计算[4]
| $ \frac{{\Delta {p_{\rm{i}}}}}{l} = \frac{1}{D}{\zeta _1}f\left( {{\rm{IPF}}} \right)\left( {\frac{{{\rho _{\rm{m}}}{V^2}}}{2}} \right), $ | (1) |
式中:Δpi为某负荷下冰浆的沿程阻力,Pa;l为二次管网长度,m;D为管道内径,m;ρm为冰浆的密度,kg/m3;IPF为冰浆中冰晶的质量百分比(含冰率);f(IPF)为阻力计算公式的修正因子,是含冰率的函数,见公式(3);ζl为当量摩擦阻力系数。在保温较好时,IPF可以取进口处的含冰率。
当量摩擦阻力系数计算公式如下[5]:
| $ \frac{1}{{\sqrt {{\zeta _1}} }} = - 2\lg \left( {\frac{{0.27\varepsilon }}{D} + \frac{{5.62}}{{\mathit{Re}_1^{0.9}}}} \right), $ | (2) |
式中,Rel为当量液相雷诺数(Rel=VD/νl,νl为水的0 ℃时的运动黏度)。
| $ f\left( {{\rm{IPF}}} \right) = 1 - 1.1451{\rm{IPF + 7}}{\rm{.743IP}}{{\rm{F}}^2}, $ | (3) |
| $ {\rho _{\rm{m}}} = \frac{{{\rho _{\rm{f}}}}}{{1 - \left( {\frac{{{\rho _{\rm{s}}} - {\rho _{\rm{f}}}}}{{{\rho _{\rm{s}}}}}} \right){\rm{IPF}}}}, $ | (4) |
式中:ρf为水的密度1 000 kg/m3;ρs为冰晶的密度920 kg/m3。
2) 局部阻力的计算
局部阻力按沿程阻力的15%计算[6],故总的阻力为
| $ \Delta {p_{\rm{i}}} = 1.15\frac{l}{D}{\zeta _1}f\left( {{\rm{IPF}}} \right)\left( {\frac{{{\rho _{\rm{m}}}{V^2}}}{2}} \right)。$ | (5) |
用冷末端在某负荷下二次泵的耗电功率为
| $ {p_{\rm{i}}} = \Delta {p_{\rm{i}}}, {G_{\rm{i}}}/\eta, $ | (6) |
式中:Pi为相应负荷下二次泵的耗电功率,W;Gi为相应负荷时的体积流量,m3/s;η为水泵的效率,取值0.65。
则水泵的年耗电费为
| $ {Y_{\rm{a}}} = \sum {{p_{\rm{i}}}{t_{\rm{j}}}{F_{\rm{d}}} \times {{10}^{ - 7}}}, $ | (7) |
式中:Ya为水泵的年耗电费用,万元/a;tj为对应某一供冷负荷的供冷时间,h/a;Fd为用电单价,元/kWh。
1.3 二次管网的年折旧费二次管网的投资主要由管道的安装费用、管道造价、保护防潮层、保温材料4部分组成。
单位长度管材的造价YD:
| $ {Y_{\rm{D}}} = {F_{\rm{g}}}{\rm{ \mathit{ π} }}\delta \gamma \left( {D + \delta } \right), $ | (8) |
式中:Fg为二次管网所用管材的价格(假设所用材料为钢管),元/t;δ为管壁的厚度,m;γ为钢管密度,t/m3。
单位管长所用保护防潮层的费用Ybh:
| $ {T_{{\rm{bh}}}} = {F_{{\rm{bh}}}}{\rm{ \mathit{ π} }}\left( {D + 2\delta + 2.1{\delta _{{\rm{bw}}}} + 0.0082} \right), $ | (9) |
式中:Fbh为保护防潮层的单价,元/m2;2.1为修正因子;0.008 2为捆扎线直径或钢带厚度,m;δbw保温层的厚度,m。
单位管长所用保温材料的费用Ybw:
| $ {Y_{{\rm{bw}}}} = 1.033{F_{{\rm{bw}}}}{\rm{ \mathit{ π} }}{\delta _{{\rm{bw}}}}\left( {D + 2{\delta _ + }1.033{\delta _{{\rm{bw}}}}} \right), $ | (10) |
式中:Fbw为保温材料的单价,元/m3;1.033为调整因数。
根据实际工程经验得出管道的土建费用与管径的函数关系[7]:
| $ {Y_{\rm{t}}} = {F_{\rm{t}}}{\rm{ \mathit{ π} }}\left( {D + 2\delta + 2{\delta _{{\rm{bw}}}}} \right)。$ | (11) |
上述各项相加为管道总投资Ygd:
| $ {Y_{{\rm{gd}}}} = \left( {{Y_{\rm{D}}} + {Y_{{\rm{bh}}}} + {Y_{{\rm{bw}}}} + {Y_{\rm{T}}}} \right)l。$ | (12) |
管道的年折旧费为
| $ \Delta {Y_{{\rm{gd}}}} = {\beta _{\rm{g}}}{Y_{{\rm{gd}}}}/10000, $ | (13) |
式中βg为管道的年折旧费率。
1.4 水泵的年折旧费水泵的价格通过设计负荷水泵功率的拟合函数进行计算,函数如下[7]:
| $ {Y_{\rm{p}}} = {k_1} + {f_1}{k_2}{p_{\rm{p}}}, $ | (14) |
式中:Pp为设计负荷水泵的功率,kW;f1,k1为拟合系数;k2为水泵设计功率的冗余值。
水泵的年折旧费为
| $ \Delta {Y_{\rm{p}}} = {\beta _{\rm{p}}}{Y_{\rm{p}}}, $ | (15) |
式中βp为水泵的年折旧率。
1.5 二次管网年冷量损失费用管道内壁对流换热热阻及管壁热阻对冷损影响较小,因此在计算时忽略其热阻。冷量损失计算公式[8]如下:
| $ q = \frac{{{t_{{\rm{w1}}}} - {t_{{\rm{w2}}}}}}{{\frac{1}{{2{\rm{ \mathit{ π} }}\lambda }}\ln \frac{{{d_2}}}{{{d_1}}} + \frac{1}{{{\rm{ \mathit{ π} }}{d_2}}}\frac{1}{{{\alpha _{\rm{s}}}}}}}, $ | (16) |
式中:tw1为管网内载冷介质的温度,℃;tw2为列车行驶隧道内空气温度,℃;d1,d2分别为管道外径及保温管道外径,m;λ为保温材料的导热系数,W/(m·k);as为管道外表面的对流换热系数W/(m2·k),按下式计算[9-10]:
| $ {\alpha _{\rm{s}}} = 11.63 + 7.0 \times \sqrt {{V_{\rm{s}}}}, $ | (17) |
式中Vs为隧道内年均环境风速,取10 m/s,则由管网内介质与隧道内空气换热所导致的年总冷量损失为
| $ Q = ql{t_{\rm{t}}}, $ | (18) |
式中tt为空调系统年运行时间。
冷量损失折算耗电量损失费用值为
| $ {Y_{\rm{Q}}} = {F_{\rm{d}}}Q/\left( {{{10}^7} \times {\rm{COP}}} \right)。$ | (19) |
水泵运行功耗最终会以热量的形式被载冷剂吸收,这部分冷量损失导致的费用按下式计算[4]:
| $ {Y_{{\rm{ws}}}} = {F_{\rm{d}}}\left( {\sum {{p_{\rm{i}}}, {t_{\rm{j}}}} } \right)/\left( {{{10}^7} \times {\rm{COP}}} \right)。$ | (20) |
| $ {Y_{{\rm{total}}}} = {Y_{\rm{a}}} + \Delta {Y_{{\rm{gd}}}} + \Delta {Y_{\rm{p}}} + {Y_{\rm{Q}}} + {Y_{{\rm{ws}}}}。$ |
参照中国建筑热环境分析专用气象数据集典型年气象参数计算了不同气候区地铁站的年负荷率,数值如表 1所示,计算相关参数如表 2所示。
| 表 1 不同气候区地铁站供冷期负荷率 |
| 表 2 计算相关参数 |
在实际的地铁站集中供冷系统中,当电价、保温层价格等各种因素都确定后,最优管道的年度费用只与输冷距离及供冷负荷有关。
文献[11]的计算实例分析在最优保温层厚度及管道内径下的二次管网单位长度年度费用(下文分析所采用的单位长度年度费用即为在最优保温层厚度及管道内径下的优化值)与供冷负荷及输冷距离的关系。图 1显示单位长度年度费用与输冷距离的关系,在输冷距离1 000~3 000 m内有些变化,但其单位长度年度费用相差只有0.000 2万元左右,可以认为在其他条件(电价、保温层价格等)确定下,单位长度年度费用只与供冷负荷有关。
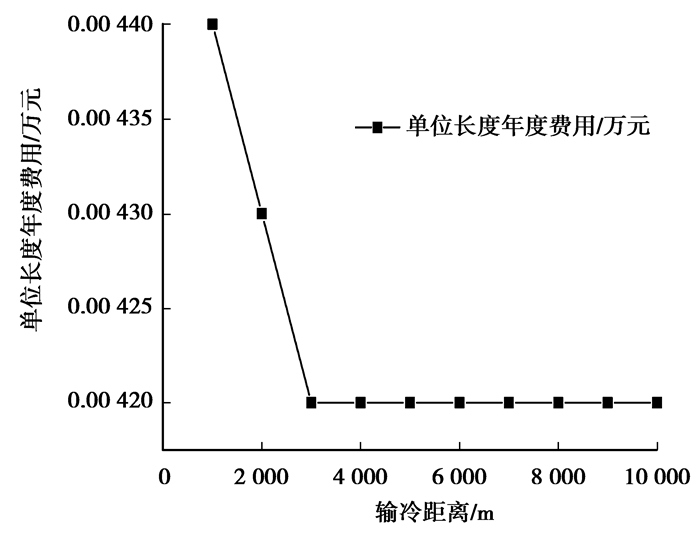
|
图 1 单位长度年度费用与输冷距离的关系 |
结果表明,当电价、保温层价格等各种因素都确定后,二次管网单位长度年度费用只与供冷负荷有关,在分析时假定多地铁站集中供冷的服务负荷范围为500~1 0000 kW之间,分别拟合了不同气候区冰蓄冷集中供冷系统与冰浆集中供冷系统供回水管道单位长度年度费用与供冷负荷的函数关系式。
假设冰蓄冷集中供冷系统供水温度为1.1 ℃,回水温度为11.1 ℃;冰浆多地铁站集中供冷载冷剂为0 ℃的冰浆,回水为10 ℃的水,分析结果如表 3所示。
| 表 3 典型城市不同系统供回水管道年度费用拟合公式 |
表 3为典型城市不同供冷系统供回水管道年度费用的拟合公式,从表 3可以得出以下结论。
1) 冰浆集中供冷系统中,同一城市,供水管道的年度费用要比回水管道小,主要原因是相同负荷下,管道输送冰浆可以携带更多的冷量,能有效减少管道投资及泵的运行费用,对于二次管网供回水管道的单位长度年度费用值,不同气候区各代表城市费用值大小依次为广州>上海>北京,如图 2所示。B、S、G分别代表北京、上海、广州。
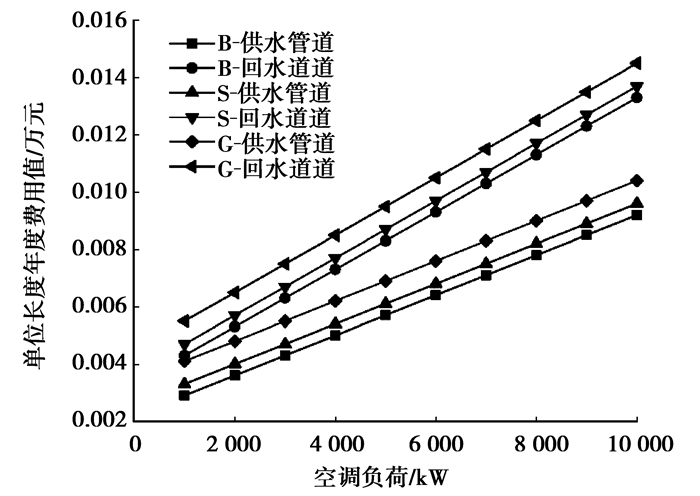
|
图 2 冰浆集中供冷二次管网单位长度年度值 |
2) 对于冰蓄冷集中供冷系统,供回水管道年度费用相差不大。供水管道的年度费用大于回水管道的年度费用,与冰浆集中供冷系统不同,主要原因是供水管道输送冷冻水温度较低,管道冷量损失较大造成的。
3) 冰浆集中供冷系统与冰蓄冷集中供冷系统的供水管道年度费用差异较大。若仅从二次管网的经济性考虑采用冰浆进行冷量输送将会较大程度降低二次管网的投资及运行维护费用,如图 4所示,图中(i)、(w)分别代表冰浆、冰蓄冷集中供冷系统。
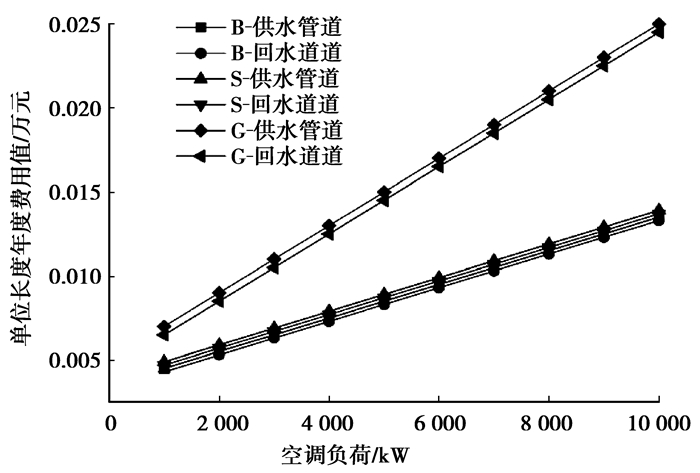
|
图 3 冰蓄冷集中供冷二次管网单位长度年度值 |
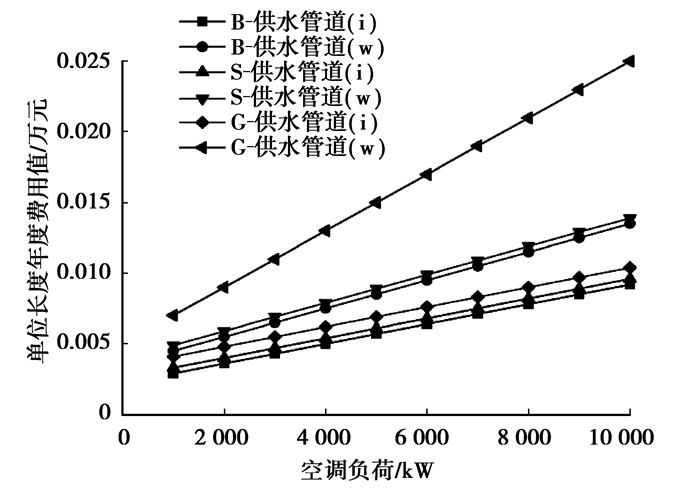
|
图 4 不同系统供水管道单位长度年度费用值对比 |
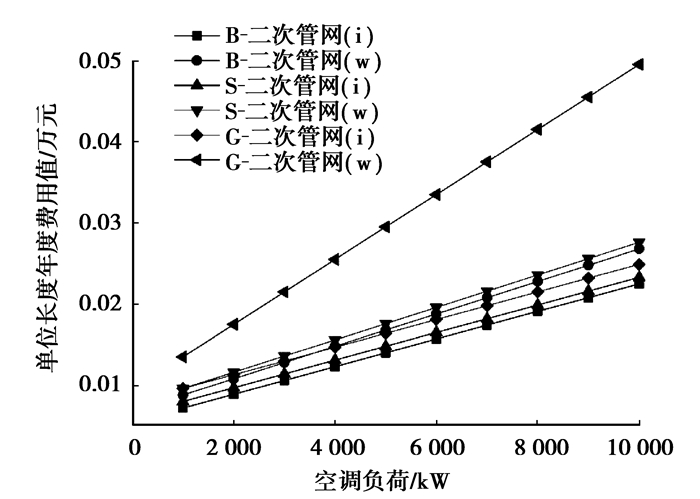
4) 图 5所示为不同气候区代表城市二次管网单位长度年度费用值(供水管道与回水管道之和)的对比。北京、上海地区采用冰浆输送与冷冻水输送冷量单位长度年度费用值差别不是很明显,广州采用冰浆输送则优势较为明显。
|
图 5 不同系统二次管网单位长度年度费用值对比 |
依据冰浆在管道内输送流动特性与传热特性的研究成果,参考实际工程造价拟合了单位管道长度年度费用值与供冷负荷的关系式,进而依据单位长度年度费用值分析了冰蓄冷与冰浆集中供冷系统在主要气候区代表城市的适用性,分析结果显示广州地区采用多地铁站冰浆集中供冷系统能有效降低输配二次管网的投资,且其优势随供冷期的增加、集中供冷服务负荷的增大及二次管网长度的增加而增加。
| [1] | Kauffeld M, Wang M J, Goldstein V, et al. Ice slurry applications[J]. International Journal of Refrigeration, 2010, 33: 1491–1505. DOI:10.1016/j.ijrefrig.2010.07.018 |
| [2] | Andrej K, Didier V, Derrick A C, et al. The fluid dynamics of ice slurry[J]. International Journal of Refrigeration, 2005, 28: 37–50. DOI:10.1016/j.ijrefrig.2004.07.010 |
| [3] | Marino G, Rahmatollah K, Per L. Experimental investigation of ice slurry flow pressure drop in horizontal tubes[J]. Experimental Thermal and Fluid Science, 2009(33): 357–370. |
| [4] | 明岗, 陈沛霖. 冰浆在水平管内流动与传热特性的试验研究[C]. 全国暖通空调制冷2000年学术年会论文集, 2000: 375-378. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGZM200000002095.htm |
| [5] | 张晓云. 超深矿井集中降温冷源关键技术研究[D]. 武汉: 武汉理工大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10497-2010036706.htm |
| [6] |
胡春胜, 张晓云.
冰浆输冷空调系统设计方法的研究[J]. 华中建筑, 2009, 27(9): 36–37.
Hu Chunsheng, Zhang Xiaoyun. Study on the design method of air conditioning system with ice slurry delivering cooling[J]. Huazhong Arhitecture, 2009, 27(9): 36–37. (in Chinese) |
| [7] |
刘金平, 杜艳国, 陈志勤.
区域供冷系统中冷冻水输送管线的优化设计[J]. 华南理工大学学报:自然科学版, 2004, 32(10): 28–31.
LIU Jinping, DU Yanguo, CHEN Zhiqin. Optimized design of the chilled water-conveying pipeline in the district cooling system[J]. Journal of South China University of Technology:Natural Science Edition, 2004, 32(10): 28–31. (in Chinese) |
| [8] |
彭金龙, 吴炜.
地铁集中供冷系统二次泵管路经济流速和经济保温厚度的确定[J]. 暖通空调, 2008, 38(7): 106–113.
PENG Jinlong, WU Wei. Determination of economic velocity and economic insulating layer thickness of secondary pump system for central cooling system of underground railway stations[J]. Journal of HVAC, 2008, 38(7): 106–113. (in Chinese) |
| [9] |
耿宇波, 王贵忠.
集中供冷工程中保冷技术与节能性的探讨[J]. 内蒙古科技与经济, 2008(5): 82–83.
GENG Yubo, WANG Guizhong. Study on insulation technology and energy efficiency of central cooling system[J]. Inner Mongolia Science Technology and Economy, 2008(5): 82–83. (in Chinese) |
| [10] |
徐承东, 徐明杰.
冷冻水管沿隧道敷设的传热学分析[J]. 城市轨道交通研究, 1999(3): 42–44.
XU Chengdong, XU Mingjie. Heat transfer analysis of chilled water pipe laying in the tunnel[J]. Urban Mass Transit, 1999(3): 42–44. (in Chinese) |
| [11] |
王群, 张旭.
地铁冰浆集中供冷系统二次管网保温层厚度及管道内径的优化[J]. 暖通空调, 2011, 41(7): 104–109.
WANG Qun, ZHANG Xu. Optimization of inner diameter and insulating layer thickness of secondary pump system for central cooling system of underground railway stations with ice slurry[J]. Heating Ventilation & Air Conditioning, 2011, 41(7): 104–109. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

