2. 湘潭大学 土木工程与力学学院, 湖南 湘潭 411105
2. School of Civil Engineering and Mechanics, Xiangtan University, Xiangtan, Hunan 411105, China
随着我国内陆地区经济的发展,环湖经济区逐渐形成,修建于湖相软基上的城际道路越来越常见。由于湖区地势平坦,软基通常较矮,在交通动荷载影响下容易产生不均匀沉降,引起路面结构破坏[1]。因此,有必要对循环动荷载作用下湖相软土的轴向累积应变、动孔隙水压力、动弹性模量、动强度和阻尼比等动力特性进行专门研究[2-6]。
通过循环振动三轴试验得到的软土动力特性指标常受到动应力幅值、振动频率、固结围压和固结应力比等加载因素的影响,这些因素对软土动力特性的影响程度往往不同,因此,需要分析各个因素对特性指标影响的显著性。为了解决此类问题,敏感性分析方法被成功应用到了岩土工程领域中[7-12]。王辉和陈卫忠[8]研究了隧道围岩变形对围岩弹性模量、泊松比、粘聚力和内摩擦角的敏感性,表明对于拱顶沉降,弹性模量比其他参数更为敏感,而对于周边收敛,泊松比、内摩擦角和粘聚力要比弹性模量更为敏感。袁维等[9]基于正交试验设计法和熵权决策法,对大坝透镜体进行了参数敏感性分析,研究表明透镜体的垂直位置和面积比率是最关键的几何影响因素,粘聚力和内摩擦角是最关键的材料影响因素,建议在评价坝体稳定性时应综合考虑坝顶位移与安全系数2个指标。陈昌富等[11]采用敏感性分析方法对刚性抗滑桩嵌固深度的可靠性受岩土体物理力学参数影响的显著性进行了分析,表明抗滑桩临界深度对滑体重度、滑动面摩擦角及粘聚力的敏感性较强,对嵌固段地层内摩擦角和粘聚力的敏感性次之。
根据洞庭湖区软土的循环动三轴试验结果,研究动应力幅值、振动频率和固结围压等因素对湖相软土轴向累积应变、动孔隙水压力和动弹性模量等动力特性的影响,通过敏感性分析寻求各因素中的量化关系,找出影响软土动力特性指标最显著的因素,为湖相软土地基的沉降分析和加固处理提供参考。
1 软土动三轴试验 1.1 试验条件洞庭湖区分布着广泛的湖相沉积淤泥、淤泥质粘性土、灰色粘土和软粉砂质粘土。选取沅江南洞庭湖区典型的淤泥质粘性土为研究对象,通过常规土工试验,得到其基本物理力学性质指标,如表 1所示。试样用原状土制备,直径为39.1 mm,高为80.0 mm,试验前试样充分饱和,饱和度均达到97%以上。试验在DDS-70微机控制单向电磁式振动三轴仪上进行,该三轴仪轴向最大压力为1 370 N,侧向压力为0~0.6 MPa,反压为0~0.3 MPa,频率范围为1~10 Hz,最大允许轴向位移为20 mm。
| 表 1 南洞庭湖区软土物理力学性质指标 |
采用正弦式荷载对车辆荷载进行模拟,同时,以不同的动应力幅值和振动频率模拟交通动荷载的大小与变化,用不同围压模拟软土的埋置深度。动应力幅值的大小与汽车荷载、车辆构造、路面性能、路表状况及行车速度等因素有关,试验选取20、40、60 kPa 3种情况进行考虑。振动频率主要依据汽车荷载对路面的振动频率来确定,它与行车速度、路面平整度及汽车的减震系统等因素有关,一般认为荷载频率为3.0 Hz时,大致相当于汽车行驶速度70 km/h[13],试验动荷载的加载频率取1.0、3.0、5.0 Hz 3种情况。围压由软土埋置深度决定,取50、100、150 kPa 3种情况。
1.2 正交试验设计正交试验是一种科学安排与分析多因素试验的方法,它采用正交表科学地挑选试验条件和安排试验,以减少试验次数,并能通过这些条件下的试验结果推断出各因素对试验指标影响的显著程度[14]。在正交试验中,把所考查的试验结果称为指标,把影响试验指标的条件称为因素,把每个因素不同的数值称为水平[15]。考虑动应力幅值、振动频率和围压3种加载因素,每个因素取3种水平(见表 2)。因此,可按L9(34)进行正交表头设计,共需做9次试验(见表 3)。按照正交试验设计的条件进行动三轴试验,得到各次试验软土的动力特性指标,则可通过敏感性分析进一步判断出各因素对指标的影响程度。
| 表 2 动力特性的影响因素 |
| 表 3 正交试验设计(L9(34)) |
软土在循环动荷载作用下的动力特性有轴向累积应变、动孔隙水压力和动弹性模量等。
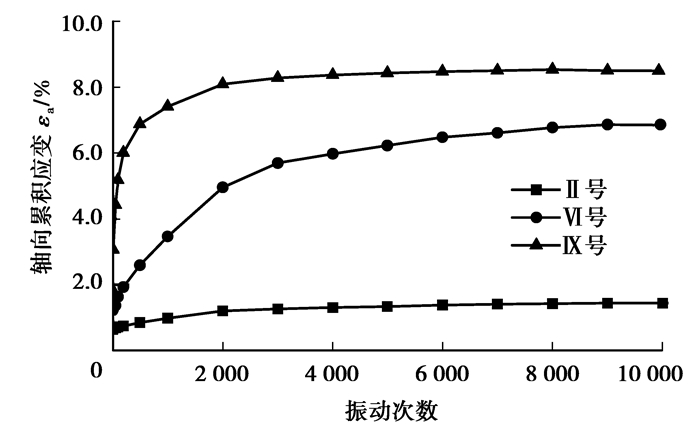
2.1 轴向累积应变在交通动荷载作用下,软土的变形规律十分复杂。由软土轴向累积应变随荷载振动次数N的变化发展曲线(见图 1)可知,当振动次数N小于500时,轴向累积应变随荷载振动次数的增加而急剧增长,当振动次数N介于500~2 000时,轴向累积应变进入缓慢增长阶段,而当振动次数N超过2 000时,轴向累积应变增长达到稳定阶段,之后基本保持不变。这就说明,受交通动荷载影响的道路工后沉降主要发生在运营初期,随着时间的推移,该部分沉降逐步稳定。
|
图 1 轴向累积应变随振动次数的变化曲线 |
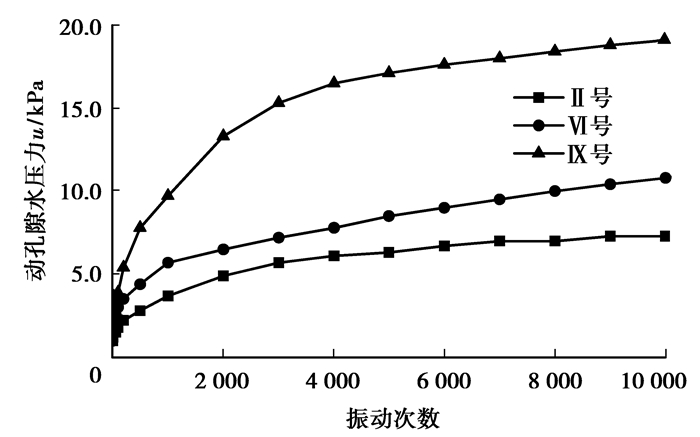
交通动荷载作用下孔隙水压力的发展是引起饱和土体变形和强度变化的根本因素之一。从试验结果(见图 2)可知,动孔隙水压力在加载初期均迅速增大,然后变化曲线曲率增加,孔隙水压力的增长趋势减缓,但仍保持一定的增长速率。经过长时间的变化发展后,部分试样动孔隙水压力的增长进入稳定增长阶段,还有个别试样动孔隙水压力在振动次数达到10 000次时仍持续增长,增长曲线为破坏型曲线。
|
图 2 动孔隙水压力随振动次数的变化曲线 |
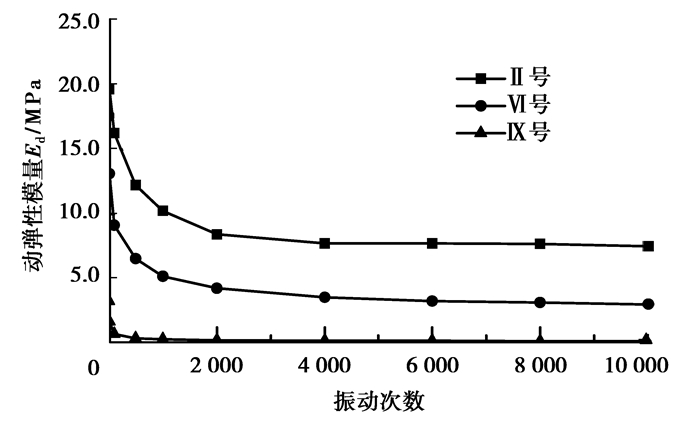
在根据动三轴试验绘制的动应力动应变关系曲线中,从原点到滞回圈顶点连线的斜率即为动弹性模量,它反映了土体在循环荷载作用下弹性变形阶段的应力应变关系。从第Ⅱ、Ⅵ、Ⅸ号试样动弹性模量Ed与振动次数N的关系曲线(见图 3)可以看出,随着振动次数的增加,动弹性模量迅速衰减,尤其是在振动初期其衰减最为明显。当振动次数达到2 000次时,动弹性模量趋于稳定,其最终稳定值(N=10 000时)不足动弹性模量初始值的30%。
|
图 3 动弹性模量随振动次数的变化曲线 |
为了使软土动力特性指标具有可比性,分别取N=1 000和N=10 000时的轴向累积应变、动孔隙水压力和动弹性模量进行对比分析。表 4为按正交设计方案进行动三轴试验得到的结果汇总。
| 表 4 软土动力特性指标试验结果 |
若将这些动力特性指标ψ视为n个影响因素的函数,则ψ可以表示为
| $ \psi = f\left( {{x_1}, {x_2}, \cdots, {x_n}} \right) $ | (1) |
式中:ψ为软土动力特性指标,如轴向累积应变、动孔隙水压力和动弹性模量等;x1,x2,…,xn为影响软土动力特性的各种因素,如动应力幅值、振动频率和围压等。
软土动力特性指标ψ的多因素极差分析方法是指先对各因素相同水平下的指标求平均值,然后将各水平下指标平均值中的最大值减去最小值得到极差,并对各因素下的指标极差进行排序来评价各因素对指标的影响程度。动力特性指标ψ的极差计算方法如下[9]:
| $ {K_{ij}} = \frac{1}{m}\sum\limits_{k = 1}^m {{\psi _{ij\;k}}}, $ | (2) |
| $ {R_{\rm{j}}} = \max \left\{ {{K_{1j}}, {K_{2j}}, \cdots, {K_{rj}}} \right\}-\min \left\{ {{K_{1j}}, {K_{2j}}, \cdots, {K_{rj}}} \right\}, $ | (3) |
式中,Kij为j因素i水平下各次试验结果指标的平均值;ψijk为j因素i水平下第k次试验结果的指标值;m为j因素在i水平下的试验次数;r为各因素的水平数;Rj为j因素影响下动力特性指标ψj的极差值,极差值越大说明该因素水平的改变对试验指标的影响也越大。
若给定一基准因素序列X*=(x1*,x2*,…,xn*),对应的基准试验指标为ψ*=f(X*),令各参数发生变化致使动力特性指标ψ偏离基准状态ψ*,然后对其偏离的趋势和程度进行分析,这种方法即为参数敏感性分析。软土动力特性指标ψ的单因素敏感性分析是通过各动力特性指标的相对变化率与各因素的相对变化率的比值来衡量的,指标ψ对j因素的敏感度Sj写成离散形式为[8]
| $ {S_{\rm{j}}} = \left| {\frac{{\left( {\frac{{\Delta {\psi _{\rm{j}}}}}{{{\psi _{\rm{j}}}^*}}} \right)}}{{\left( {\frac{{\Delta {x_{\rm{j}}}}}{{{x_{\rm{j}}}^*}}} \right)}}} \right| = \left| {\frac{{\Delta {\psi _{\rm{j}}}}}{{\Delta {x_{\rm{j}}}}} \cdot \frac{{{x_{\rm{j}}}^*}}{{{\psi _{\rm{j}}}^*}}} \right|, $ | (4) |
式中:Δψj/ψj*为j因素影响下动力特性指标ψ的相对变化率;Δxj/xj*为j因素xj的相对变化率。
通过上述敏感度即可判断软土动力特性指标对各影响因素的敏感程度,敏感度越大,说明软土动力特性指标受该因素的影响越显著。
3.2 动力特性多因素极差分析对各种因素影响下的湖相软土动力特性指标εa进行极差分析,从分析结果(见表 5)可知,各因素对指标εa的影响程度排序均为:动应力幅值Δσd>围压σ3c>振动频率f。而且还可以看出,当N=10 000时,如果要求循环荷载作用下软土的轴向变形(εa)最小,则应尽可能地减小动应力幅值,同时增大振动频率和围压。
| 表 5 轴向累积应变极差分析表 |
将各种加载因素影响下的湖相软土动力特性指标u进行极差分析(见表 6)。结果表明,各因素对指标u的影响程度排序均为:动应力幅值Δσd>振动频率f>围压σ3c。同时发现,若要使N=10 000时指标u的值最小,最优试验条件为:Δσd =20 kPa,f =5 Hz,σ3c=150 kPa,尽可能地采用较小的动应力幅值、较大的振动频率和围压。
| 表 6 动孔隙水压力极差分析表 |
对各种因素影响下的湖相软土动力特性指标Ed进行极差分析,结果如表 7所示。由此可见,各因素对指标Ed的影响程度排序均为:动应力幅值Δσd>围压σ3c>振动频率f。如果要使N=10 000时指标Ed的值最大,最优试验条件为:Δσd =20 kPa,f =3 Hz,σ3c=150 kPa。
| 表 |
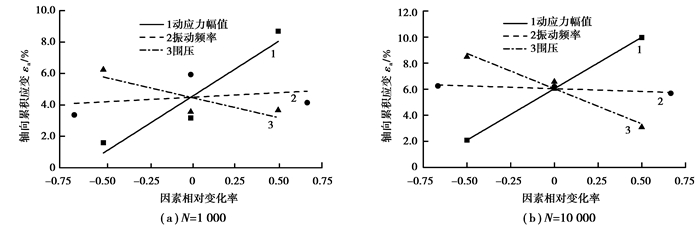
从软土轴向累积应变εa与各单因素相对变化率之间的关系曲线(见图 4)可知,轴向累积应变始终随动应力幅值的增大而线性增大,而受振动频率的影响较小,且规律不一致,当N=1 000时,轴向累积应变随振动频率的增大而缓慢增大,当N=10 000时,反而随振动频率的增大而有所减小。轴向累积应变随围压的增大而线性减小,这是由于软土在较大的围压下固结时,其内部绝大多数孔隙均被压缩,故在动荷载作用下进一步发生的变形较小。
|
图 4 轴向累积应变与因素相对变化率的关系曲线 |
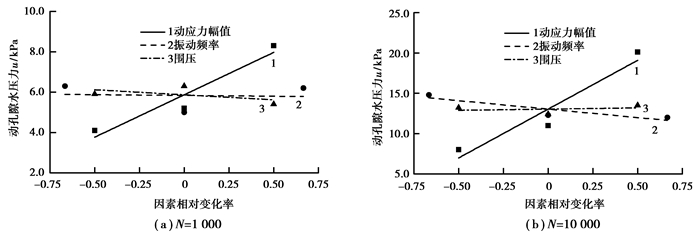
图 5为软土动孔隙水压力与各单因素相对变化率之间的关系曲线,由该曲线可知动孔隙水压力随动应力幅值的增大而增大,动应力幅值增大或减小50%,动孔隙水压力相应地增大或减小2.10~6.01 kPa。这是因为动应力幅值越大,循环荷载蕴含的能量越多,转移到软土上的动能也越大,使土颗粒间发生相互运动和重新排列的趋势越强烈,因而在土体内产生的孔隙水压力也越大。动孔隙水压力受振动频率和围压的影响相对较小,振动频率或围压改变50%,对应的动孔隙水压力只改变0.04~1.05 kPa或0.15~0.25 kPa。
|
图 5 动孔隙水压力与因素相对变化率的关系曲线 |
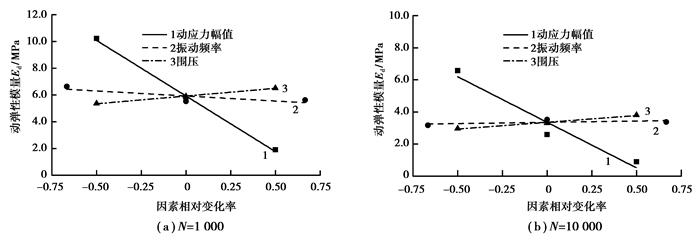
图 6给出了软土动弹性模量与各单因素相对变化率之间的关系曲线。从图 6可见,动弹性模量随动应力幅值的增大而显著减小,而受振动频率和围压的影响相对较小。动应力幅值增大或减小50%,动弹性模量相应地减小或增大2.84~4.15 MPa。振动频率或围压改变50%,对应的动弹性模量只改变0.08~0.38 MPa或0.42~0.58 MPa。
|
图 6 动弹性模量与因素相对变化率的关系曲线 |
以各因素的2水平为基准,通过减小或增加变动到1水平和3水平,分别按式(4)求得单一变动下动力特性指标的敏感度,将2次变动的敏感度求平均即得到动力特性指标受各单因素影响的平均敏感度(见表 8)。从表 8可以得知,动应力幅值Δσd、振动频率f和围压σ3c这3个因素对指标εa的敏感度大小排序均为:动应力幅值Δσd>围压σ3c>振动频率f;对指标u的敏感度大小排序为:N=1 000时,动应力幅值Δσd>围压σ3c>振动频率f,N=10 000时,动应力幅值Δσd>振动频率f>围压σ3c;对指标Ed的敏感度大小排序为:动应力幅值Δσd>围压σ3c>振动频率f。由此可见,单因素敏感度分析得到的结论与极差分析的结论基本一致,唯N=1 000时各因素对动孔隙水压力的影响规律略有不同,这是因为单因素敏感性分析是建立在其他因素不变的条件下的,即忽略了各影响因素间的交互作用,这反映了单因素敏感性分析的局限性。
| 表 8 影响因素的敏感度 |
基于洞庭湖软土的动三轴试验结果,通过敏感性分析研究了湖相软土动力特性对各种外部因素的敏感性,得到以下结论。
1) 轴向累积应变随振次多呈稳定型增长,且大多数应变形成于振动开始阶段,受交通动荷载影响的道路工后沉降主要发生在运营初期。轴向累积应变始终随动应力幅值的增大而增大,随围压的增大而减小,而受振动频率影响的规律不一。各因素中,影响轴向累积应变最显著的是动应力幅值,其次是围压,最后是振动频率。
2) 动孔隙水压力随振次的增长主要表现为稳定型变化曲线,部分为破坏型曲线。动孔隙水压力随动应力幅值的增大而增大,随振动频率和围压的增大而缓慢减小。动孔隙水压力对动应力幅值的变化最为敏感,其次是振动频率,受围压的影响较小。
3) 随着振动次数的增加,动弹性模量迅速衰减,尤其是在振动初期其衰减最为明显。动弹性模量随动应力幅值的增大而显著减小,受振动频率和围压的影响相对较小。动弹性模量受动应力幅值的影响最为显著,其次是围压,影响最小的是振动频率。
| [1] | Wu D Z, Zhang Z Y. Study on thesettlement of soft soil subgrade with a crust layer[J]. Applied Mechanics and Materials, 2014, 505: 82–88. |
| [2] | Sakai A, Samang L, Miura N. Partially-drained cyclic behavior and its application to the settlement of a low embankment road on silty-clay[J]. Soils and Foundations, 2003, 43(1): 33–46. DOI:10.3208/sandf.43.33 |
| [3] |
王军, 蔡袁强, 丁光亚, 等.
双向激振下饱和软黏土动弹性模量与阻尼变化规律试验研究[J]. 岩石力学与工程学报, 2010, 29(2): 423–432.
WANG Jun, CAI Yuanqiang, DING Guangya, et al. Experimental research on changing rules of dynamic modulus and damping ratio of saturated soft clay under bidirectional exciting cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 423–432. (in Chinese) |
| [4] | Zhang J F, Andrus R D, Juang C H. Normalized shearmodulus and material damping ratio relationships[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(4): 453–464. DOI:10.1061/(ASCE)1090-0241(2005)131:4(453) |
| [5] | Gu C, Wang J, Cai Y Q, et al. Undrained cyclic triaxial behavior of saturated clays under variable confining pressure[J]. Soil Dynamics and Earthquake Engineering, 2012, 40: 118–128. DOI:10.1016/j.soildyn.2012.03.011 |
| [6] | Feng Q, Li H, Zhang Y. Research on the dynamic characteristics of clay[J]. Applied Mechanics and Materials, 2014, 535: 764–767. DOI:10.4028/www.scientific.net/AMM.535 |
| [7] | Liu L, Liu X H. Sensitivity analysis of soil erosion in the northern loess plateau[J]. Procedia Environmental Sciences, 2010(2): 134–148. |
| [8] |
王辉, 陈卫忠.
嘎隆拉隧道围岩力学参数对变形的敏感性分析[J]. 岩土工程学报, 2012, 34(8): 1548–1553.
WANG Hui, CHEN Weizhong. Sensitivity analysis of mechanical parameters to deformation of surrounding rock in Galongla tunnel[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1548–1553. (in Chinese) |
| [9] |
袁维, 白冰, 李小春, 等.
透镜体对尾矿坝安全性影响的参数敏感性分析[J]. 中南大学学报:自然科学版, 2013, 44(3): 1174–1182.
YUAN Wei, BAI Bing, LI Xiaochun, et al. Parameters sensitivity analysis of lenticles impacting on tailings dam safety[J]. Journal of Central South University:Science and Technology, 2013, 44(3): 1174–1182. (in Chinese) |
| [10] | Yiouta M P, Nomikos P P, Mertiri E, et al. Tunnel design and sensitivity analysis[J]. Geotechnical and Geological Engineering, 2013, 31(2): 647–665. DOI:10.1007/s10706-013-9615-9 |
| [11] |
陈昌富, 杜翠翠, 张根宝.
基于双参数法刚性抗滑桩嵌固深度可靠性设计[J]. 湖南大学学报:自然科学版, 2014, 41(2): 40–46.
CHEN Changfu, DU Cuicui, ZHANG Genbao. Reliability design of the embedded depth of the rigid anti-slide piles based on bi-parameter method[J]. Journal of Hunan University:Natural Sciences, 2014, 41(2): 40–46. (in Chinese) |
| [12] | Cao L, Qian S G, Wang H M, et al. Analysis on slope stability based on factor sensitivity[J]. Applied Mechanics and Materials, 2014, 475: 1528–1533. |
| [13] |
闫春岭, 唐益群, 刘莎.
地铁荷载下饱和软黏土累积变形特性[J]. 同济大学学报:自然科学版, 2011, 39(7): 978–982.
YAN Chunling, TANG Yiqun, LIU Sha. Accumulative deformation characteristics of saturated soft clay under subway loading in Shanghai[J]. Journal of Tongji University:Natural Science, 2011, 39(7): 978–982. (in Chinese) |
| [14] |
李炎隆, 李守义, 丁占峰, 等.
基于正交试验法的邓肯-张E-B模型参数敏感性分析研究[J]. 水利学报, 2013, 44(7): 873–879.
LI Yanlong, LI Shouyi, DING Zhanfeng, et al. The sensitivity analysis of Duncan-Chang E-B model parameters based on the orthogonal test method[J]. Journal of Hydraulic Engineering, 2013, 44(7): 873–879. (in Chinese) |
| [15] | 黄志福. 交通循环荷载作用下粉土路堤动力特性试验研究[D]. 天津: 天津大学建筑工程学院, 2011: 9-12. http://cdmd.cnki.com.cn/Article/CDMD-10056-1012008444.htm |
 2014, Vol. 37
2014, Vol. 37


