2. 中国石油西部管道公司乌鲁木齐输油气分公司, 乌鲁木齐 830000;
3. 中国石油西南管道公司兰成渝输油分公司, 成都 610069
2. The Western Pipeline Company, Urumqi 830000, China;
3. LAN-CHENG-YU Oil Transportation Sub-Company, Chengdu 610069, China
X60钢相当于国内L415钢,多用于输送石油、天然气等的大口径焊接钢管[1],其屈服强度高、塑性好,可承受较高压力,在管线钢年产量及实际应用中,占有相当大的份量。在万能实验机上,对X60管线钢标准试件进行拉伸实验,实验结果表明:X60管线钢进入塑性状态后,其应力应变曲线表现为典型的非线性,没有明显的屈服平台;应变不仅与应力状态有关,而且还与变形历史有关[2]。进一步研究目前应用比较广泛的Ramberg-Osgood本构关系,发现发现ε≤εP0.2时,Ramberg-Osgood本构方程能够比较准确地反映X60管线钢的拉伸应力应变关系,但当ε>εP0.2时,基于Ramberg-Osgood模型所得理论本构曲线与实验结果有较大的误差[3]。基于此,笔者对Ramberg-Osgood本构模型做出了修正[4],提出了X60管线钢在单向拉伸状态下的全局二段式应力应变关系式。
长期以来,基于应力的判据处于主导地位。然而,随着研究的深入和发展,越来越多的研究表明在某些特殊工况环境下,如在冻土、地震和滑坡等地质灾害区域的地表位移影响下,管道承受的应力虽然已经达到或超过应力判别准则的要求,但是管道依然能够满足输送要求[5],这种情况下基于应力的判据就显得过于保守,由此,产生了所谓的基于应变的管道失效判据,即认为管道的失效不再由应力控制,而是由应变控制[6]。挪威船级社(DNV)1982年就提出将基于应变的设计准则与基于应力的设计准则结合起来,并于1996年出版了海底管线的极限设计准则,提出了多种载荷条件下的极限状态分析方法[7]。2003年由美国管道安全部(OPS)及矿业管理部(MMS)撰写了《以应变为基础的管道设计》这一研究报告,系统地阐述了以应变为基础的管道设计方法与建议[7-8]。现行的基于应变的管道设计准则包括:ASME B31.8、DNV-OS-F101《海底管道系统》,CSA-Z662《油气管道系统》、API 1104、ASCE《埋地管道设计指导》和ABS2001等。其中,DNV-OS-F101(2000)规定累计塑性应变超过0.3%时需要进行工程临界评价(ECA);累计塑性应变超过2.0%时不仅需要进行工程临界评价(ECA),还需要满足材料的其他附加要求[8]。需要注意的是长输管道由数量众多的螺旋焊缝和对接焊缝焊接而成,在外载荷作用下,拉伸应变达到或超过极限值,可导致管道在焊缝处拉断失效。可见,管材失效不仅取决于材料本身的力学性能,还与其焊接性能有直接的关系;对管道的失效准则进行研究,以解决管道力学风险状态的准确判断,具有重要的价值。此外,精确描述X60管线钢的应力应变关系、建立其失效判据也是管道结构受力及稳定性分析等相关研究工作的基础。
1 X60(L415)管线钢的实验本构关系在万能材料实验机上,选取10件X60管线钢标准试件,对其进行拉伸实验,实验后的σ-ε曲线见图 1(a)。选取其中一条典型的σ-ε曲线作为此钢材试样本构关系修正的计算依据,见图 1(b)[9],其力学特征参数见表 1。其中,σ为应力,MPa;ε为应变,无量纲,常用%表示。
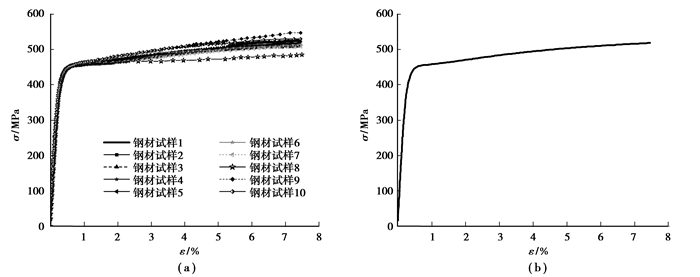
|
图 1 X60(L415)管线钢的拉伸实验应力应变曲线 |
| 表 1 X60(L415)管线钢的力学特征参数 |
根据上述X60管线钢的实验本构关系曲线,这里提出全局二段式管线钢应力应变模型。
第一阶段为应力在条件屈服极限范围内,即ε≤εP0.2时,采用传统的Ramberg-Osgood本构模型来表示单轴非线性应力应变关系[3],此模型视总应变为弹性应变εe和塑性应变εP之和,其形式见公式(1)。
| $ {\varepsilon _{总}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{P}}} = \frac{\sigma }{{{E_0}}} + {\left( {\frac{\sigma }{K}} \right)^n}, $ | (1) |
式中:ε总为总应变,无量纲;εe为弹性应变,无量纲;εP为塑性应变,无量纲;E0为材料初始弹性模量,MPa,取值为2.07×105 MPa;K为应变硬化相关系数,MPa;n为应变硬化指数,反映材料应力应变曲线的非线性程度,无量纲。
这里,令
| $ {\varepsilon _{总}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{P}}} = \frac{\sigma }{{{E_0}}}\left( {1 + \frac{r}{{n + 1}}{{\left( {\frac{\sigma }{{{\sigma _{\rm{s}}}}}} \right)}^n}} \right)。$ | (2) |
对于X60管线钢,n=10,r=9,X60管线钢的本构关系方程可表达为公式(3)[3]。
| $ \varepsilon = \frac{\sigma }{{{E_0}}}\left[{1 + \frac{9}{{11}}{{\left( {\frac{\sigma }{{360}}} \right)}^{10}}} \right]。$ | (3) |
如图 2所示,将Ramberg-Osgood方程建立的本构关系曲线与实验本构关系曲线进行对比,可见,当ε≤εP0.2时,Ramberg-Osgood本构方程能够比较准确地反映X60管线钢的应力应变曲线,但当ε>εP0.2时,基于上述模型所得理论本构曲线与实验结果有较大的误差。因此对于超出εP0.2的大应变,有必要对Ramberg-Osgood模型做出修正。
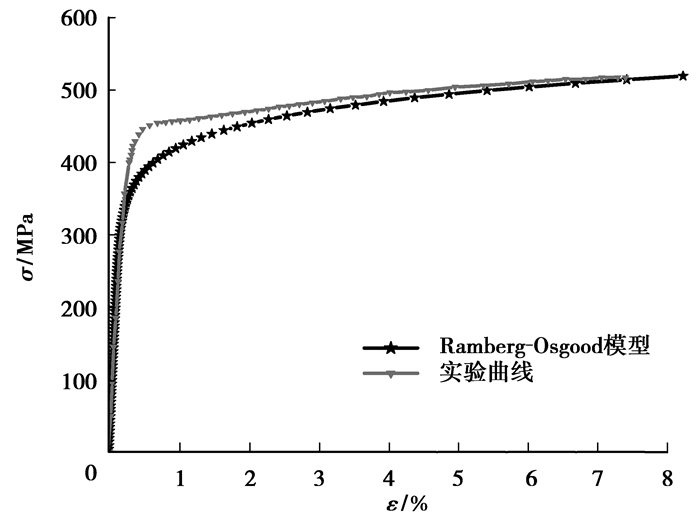
|
图 2 X60管线钢的Ramberg-Osgood模型与实验应力应变曲线对比图 |
由X60的实验拉伸本构关系可见:X60钢材没有明显的屈服平台,工程上常采用卸载后剩余0.2%的塑性变形所对应的应力为屈服极限[10]。根据实验数据,提出用条件屈服极限σP1.0来代替极限应力,在σP0.2和σP1.0间采用如下表达式,即
| $ {\varepsilon _{总}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{P}}} = \frac{{\sigma - {\sigma _{{\rm{P0}}{\rm{.2}}}}}}{{{E_{0.2}}}} + \left[{0.008 + \left( {{\sigma _{{\rm{P1}}{\rm{.0}}}}-{\sigma _{{\rm{P0}}{\rm{.2}}}}} \right)\left( {\frac{1}{{{E_0}}}-\frac{1}{{{E_{0.2}}}}} \right)} \right]\\ \times \left( {\frac{{\sigma - {\sigma _{{\rm{P0}}{\rm{.2}}}}}}{{{\sigma _{{\rm{P1}}{\rm{.0}}}} - {\sigma _{{\rm{P0}}{\rm{.2}}}}}}} \right){n_{0.2, 1.0}} + {\varepsilon _{{\rm{P0}}{\rm{.2}}}}。$ | (4) |
式中:σP0.2为卸载后剩余0.2%的塑性变形所对应的应力,MPa;E0.2为应力等于σP0.2时的切线模量,MPa;σP1.0为卸载后剩余1%的塑性变形所对应的应力,MPa;n0.2,1.0为描述σP0.2和σP1.0间曲线段的应变硬化指数,无量纲,其值可根据模型与实验所得应力应变曲线的符合程度求出[10];εP0.2为卸载后剩余0.2%的塑性变形所对应的应变,无量纲,εP0.2=0.2%+ε0。
综合上述分析,全局二段式管线钢应力应变关系可表达为式(5)所示。
| $ \varepsilon = \left\{ \begin{array}{l} \frac{\sigma }{{{E_0}}}\left( {1 + \frac{r}{{n + 1}}{{\left( {\frac{\sigma }{{{\sigma _{\rm{s}}}}}} \right)}^n}} \right), \sigma \le {\sigma _{{\rm{P0}}{\rm{.2}}}};\\ \frac{{\sigma - {\sigma _{{\rm{P0}}{\rm{.2}}}}}}{{{E_{0.2}}}} + \left[{0.008 + \left( {{\sigma _{{\rm{P1}}{\rm{.0}}}}-{\sigma _{{\rm{P0}}{\rm{.2}}}}} \right)\left( {\frac{1}{{{E_0}}}-\frac{1}{{{E_{0.2}}}}} \right)} \right] \\\times \left( {\frac{{\sigma - {\sigma _{{\rm{P0}}{\rm{.2}}}}}}{{{\sigma _{{\rm{P1}}{\rm{.0}}}} - {\sigma _{{\rm{P0}}{\rm{.2}}}}}}} \right){n_{0.2, 1.0}} + {\varepsilon _{0.2}}{\sigma _{{\rm{P0}}{\rm{.2}}}} < \sigma \le {\sigma _{{\rm{P1}}{\rm{.0}}}}。\end{array} \right. $ | (5) |
由实验曲线可见,σP0.2=410 MPa,σP1.0=455.43 MPa;又:
| $ {n_{0.2, 1.0}} = 12.255\left[{\frac{{{E_{0.2}}}}{{{E_0}}}} \right]\left[{\frac{{{\sigma _{{\rm{P1}}{\rm{.0}}}}}}{{{\sigma _{{\rm{P0}}{\rm{.2}}}}}}} \right] + 1.037 = 2.27, $ |
具体地,当σP0.2 < σ≤σP1.0时,由公式(5)可得:
| $ \begin{array}{*{20}{c}} {\varepsilon = \frac{{\sigma - 410}}{{18646.43}} + 0.00566 \times }\\ {\left( {\frac{{\sigma - 410}}{{45.43}}} \right)2.27 + 0.0037。} \end{array} $ | (6) |
按照σP0.2的技术规格书要求,其值为360~530 MPa,通过与实验曲线的拟合修正,式(6)可修正为
| $ \begin{array}{*{20}{c}} {\varepsilon = \frac{{\sigma - 410}}{{16535.43}} + 0.00547 \times }\\ {\left( {\frac{{\sigma - 410}}{{45.43}}} \right)2.8 + 0.0028。} \end{array} $ | (7) |
由图 3可见,修正后的公式也适用于σ≥σP1.0时X60管线钢的本构关系。
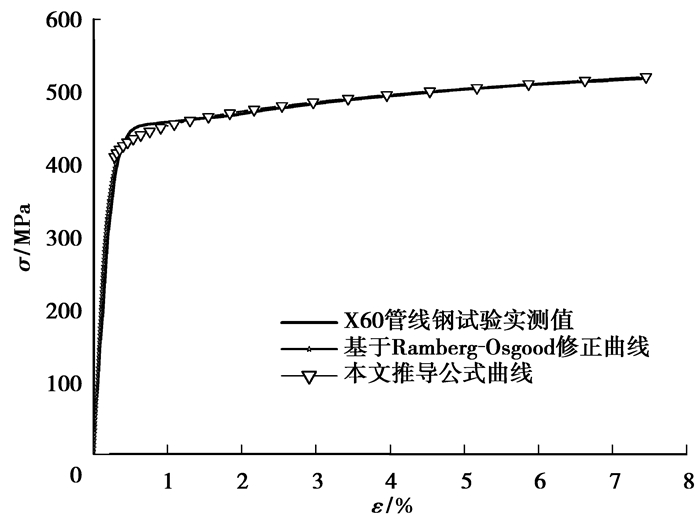
|
图 3 X60管线钢的Ramberg-Osgood本构关系、全局二段式本构关系与实验本构关系对比图 |
分析X60管线钢的Ramberg-Osgood本构关系可知:r和n值越小,曲线的曲率越大,且r小于n+1时,曲率增大;r大于n+1时,曲率变小。任意取两组拉伸实验曲线确定的参数,如:(0.031 29,50.448 9),(0.103 54,186.02)代入上式,得r=2,n=6,对比后发现,参数r=2,n=6与实验曲线更加吻合。
由此,X60管线钢材料拉伸应力应变关系可表述为
| $ \varepsilon = \left\{ \begin{array}{l} {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{P}}} = \frac{\sigma }{{{E_0}}}\left( {1 + \frac{2}{7}{{\left( {\frac{\sigma }{{{\sigma _{\rm{s}}}}}} \right)}^6}} \right), \sigma \le {\sigma _{0.2}};\\ \frac{{\sigma - 410}}{{16535.43}} + 0.00547 \times \left( {\frac{{\sigma - 410}}{{45.43}}} \right)2.8 + 0.0028, \sigma > {\sigma _{0.2}}。\end{array} \right. $ | (8) |
依据公式(8)绘制的X60拉伸应力应变关系如图 3所示。对比其与拉伸实验应力应变关系曲线可见,公式(8)建立的X60管线钢的拉伸应力应变关系与实验结果更加吻合,可作为该管线钢实际拉伸本构关系。
3 管道失效判据长输管道受环境载荷影响,最易发生力学失效,如水灾掏空引起的管道大面积悬空、滑坡引起的意外冲击载荷、地震引起的地震波、铁路公路穿跨越处的交变载荷[9]……通常,将外部载荷引起的管道响应称为载荷控制响应,位移引起的管道结构响应称为位移控制响应。由管线钢应力应变实验曲线可见,当应力或应变达到某一临界值时,管线钢将发生强度失效或塑性失效[11]。根据是取应力还是取应变作为衡量管道失效时的准则,分别有基于应力的失效判据和基于应变的失效判据[12]。下面根据X60管线钢的实验本构关系,给出确定管道失效时应力或应变临界值的力学依据和方法。
3.1 基于应力的失效准则按照管道施工设计的规定,管道的强度计算遵循基于应力的失效准则。即在工作载荷条件下,管道本体可能出现的最大应力小于其屈服应力。由于仅在内压作用下,管道的周向薄膜应力为轴向薄膜应力的2倍[13],而滑坡、悬空、水冲、地震等外部载荷通常仅引起管道轴向应力的变化。故管道的强度应同时满足以下两个条件。
1) 基于周向应力的强度失效准则。
该准则要求管道工况条件下的周向应力应小于管线钢的许用应力,即满足下式[14]:
| $ {\sigma _\varphi } < {\left[\sigma \right]^t} = f\varphi {\sigma _{\rm{S}}}, $ | (15) |
式中:σφ为管道的周向应力,MPa;[σ]t为工作温度下管线钢的许用应力,MPa;f为设计系数,无量纲;σS为管线钢的屈服强度,MPa,取值为415 MPa;φ为焊接接头系数,无量纲,对接接头单面焊接且100%探伤时,取值为0.9。
其中,设计系数反映了管道工程中的安全裕度。输油管道的设计系数一般为0.72,随着高强度钢的使用和管道施工工艺的优化,此范围放宽到0.8[3];输气管道则根据管道通过地区沿线的人口和建筑物的密集程度,划分为4个等级:一级地区为0.72,二级地区为0.6,三级地区为0.5,四级地区为0.4[3]。
2) 基于组合应力条件的弹性失效准则。
通常管道除承受油气内压、土壤外压外,还可能存在安装载荷、地质灾害引起的意外载荷、周围环境引起的环境载荷等,管道本体除周向应力外,还存在轴向应力,对于厚壁管道,径向应力也不能忽略,即管道处于三向应力状态下。按照Lame公式,厚壁圆筒在设计条件下的三向应力表达式[13]为
| $ \left. \begin{array}{l} {\sigma _\varphi } = \frac{{{P_{\rm{i}}}{R_{\text{i}}}^2 - {P_{\rm{o}}}{R_{\text{o}}}^2}}{{{R_{\text{o}}}^2 - {R_{\text{i}}}^2}} + \frac{{\left( {{P_{\rm{i}}} - {P_{\rm{o}}}} \right){R_{\text{i}}}^2{R_{\text{o}}}^2}}{{{R_{\text{o}}}^2 - {R_{\text{i}}}^2}} \times \frac{1}{{{r^2}}}\\ {\sigma _{\rm{r}}} = \frac{{{P_{\rm{i}}}{R_{\text{i}}}^2 - {P_{\rm{o}}}{R_{\text{o}}}^2}}{{{R_{\text{o}}}^2 - {R_{\text{i}}}^2}} - \frac{{\left( {{P_{\rm{i}}} - {P_{\rm{o}}}} \right){R_{\text{i}}}^2{R_{\text{o}}}^2}}{{{R_{\text{o}}}^2 - {R_{\text{i}}}^2}} \times \frac{1}{{{r^2}}}\\ {\sigma _\theta } = \frac{{{P_{\rm{i}}}{R_{\text{i}}}^2 - {P_{\rm{o}}}{R_{\text{o}}}^2}}{{{R_{\text{o}}}^2 - {R_{\text{i}}}^2}} \end{array} \right\}。$ | (16) |
按照第三强度理论(最大剪应力理论),有如下公式[15]:
| $ \begin{array}{*{20}{c}} {{\tau _{\max }} = \frac{1}{2}{{\left( {{\sigma _\varphi } - {\sigma _{\rm{r}}}} \right)}_{{\rm{r}} = {R_i}}} \le \frac{1}{2}{{\left[\sigma \right]}^t}, }\\ \end{array} $ |
即
| $ {{{\left( {{\sigma _\varphi } - {\sigma _{\rm{r}}}} \right)}_{{\rm{r}} = {R_i}}} \le {{\left[\sigma \right]}^t}。} $ | (17) |
式中:Pi为内压,MPa;Ri为内径,mm;Po为外压,MPa;Ro为外径,mm;r为管道筒体任意一点的半径,mm;σr为径向薄膜应力,MPa;σθ为轴向薄膜应力,MPa。
将式(16)代入式(17),得第三强度理论条件下管道的强度失效准则:
| $ \frac{{2\left( {{P_{\rm{i}}} - {P_{\rm{o}}}} \right)R_{{\text{o}}}^2}}{{R_{{\text{o}}}^2 - R_{{\text{i}}}^2}} \le {\left[\sigma \right]^t}。$ | (18) |
按照第四强度理论(最大形状改变比能理论),认为最大形状改变比能达到一定值时发生屈服,屈服条件的表达式[15]为
| $ {\left| {\frac{1}{{\sqrt 2 }}\sqrt {{{\left( {{\sigma _\varphi } - {\sigma _\theta }} \right)}^2} + {{\left( {{\sigma _\theta } - {\sigma _{\text{r}}}} \right)}^2} + {{\left( {{\sigma _{\text{r}}} - {\sigma _\varphi }} \right)}^2}} } \right|_{{\text{r}} = {R_{\text{i}}}}} \leqslant {\left[ \sigma \right]^t}。$ | (19) |
将式(16)代入式(19),得第四强度理论条件下管道的强度失效准则:
| $ \sqrt 3 \frac{{\left( {{P_{\rm{i}}} - {P_{\rm{o}}}} \right)R_{{\text{o}}}^2}}{{R_{{\text{o}}}^2 - R_{{\text{i}}}^2}} \le {\left[\sigma \right]^t}。$ | (20) |
实验结果表明,基于周向应力和根据第三强度理论建立的X60管线钢强度失效准则过于保守,通常采用基于第四强度理论建立的管线钢强度失效准则,在此准则条件下,管道失效时的临界应力为:
按照空间几何分布,管道均匀变形可分为拉伸变形、压缩变形和椭圆化变形[3]。拉伸(压缩)变形通常由内压、覆土压力、管道自重、温度应力、地质灾害等。椭圆化变形则主要由外压引起。为防止过量变形引发管道失效,需要限制管道拉伸应变、压缩应变和椭圆化变形[3]。
国内现行的管道设计标准大多都采用基于应力的设计准则,即保证管道在外载荷作用下的等效应力不高于管材的屈服极限与安全系数的乘积。这种设计方法曾经为管道安全运营提供了充分的力学安全保障。但当管道受地震、泥石流、滑坡、振动载荷等地质载荷影响时,管道应力超过弹性范围发生塑性变形,此时,少量塑性范围内,管道依然可以安全工作,基于应力的弹性失效准则已不再适用,宜采取以应变为失效判据的安全准则。
此外,长输管道由数量众多的螺旋焊缝和对接焊缝焊接而成,在外载荷作用下,拉伸应变达到或超过极限值,可导致管道在焊缝处拉断失效[16]。为考虑焊缝对管道强度和刚度的影响,在此进行了含焊缝试件的拉伸实验。试件分3组进行:含螺旋焊缝试件、含对接焊缝试件以及无焊缝母材试件,以得出焊缝对管材的影响。
试样采用圆棒形标准试件。考虑焊缝的不均匀性或焊缝缺陷对测试的影响,试件实验前已进行射线和超声检测,缺陷在1级及以下。使用万能数字拉伸实验机进行室温拉伸实验,测量其应力应变曲线、屈服强度、抗拉强度以及断后延伸率等数据。实验结果如表 2、3、4所示。其中表 2为含螺旋焊缝试件拉伸实验数据表,表 3为含对接焊缝的拉伸实验数据表,表 4为无焊缝母材的拉伸实验数据表。
| 表 2 含螺旋焊缝试件拉伸实验数据 |
| 表 3 含对接焊缝试件拉伸实验数据 |
| 表 4 无焊缝母材拉伸实验数据 |
分析3种试件的拉伸数据,进行对比,如图 4所示。
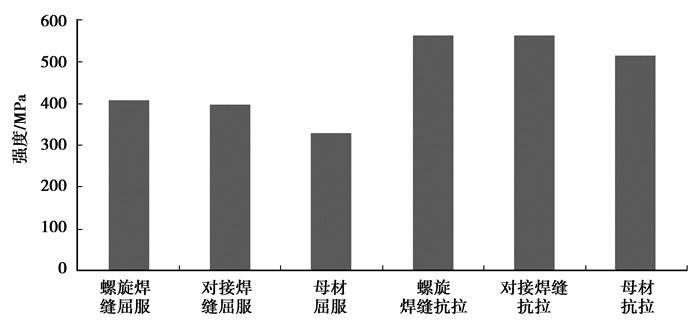
|
图 4 实验结果对比 |
由图可见,在焊接热影响区,材料硬化、脆化,导致含焊缝试件的屈服极限和强度极限明显高于无焊缝试件,而延伸率则明显低于无焊缝试件。
考虑到管材缺陷、焊缝及热影响区等的影响,建立管道拉伸应变失效准则为
| $ \varepsilon \le f{\varphi _f}\left[\varepsilon \right], $ | (21) |
式中:ε为因子化拉伸应变,无量纲,%;f为设计系数,无量钢,对输油管道,取值为0.72,对输气管道,考虑地区等级:一级地区取0.72,二级地区为0.6,三级地区为0.5,四级地区为0.4[3];φf为焊缝刚度系数,无量纲,由实验确定,考虑到管材缺陷、焊缝及热影响区等的影响,现场管道无法进行拉伸实验,根据测试结果,通常取值为0.6;[ε]为管道的许用应变,这里为弹性应变加0.3%的塑性应变,常取0.5%。
需要进行工程临界评价(ECA)和其他附加要求的应变范围为
| $ f{\varphi _f}\left[\varepsilon \right] \le \varepsilon \le f{\varphi _f}{\varepsilon _{\max }}, $ | (22) |
式中:εmax为管道的极限应变,这里指地面变形中允许的拉应变极限值,取值为2%。
1) 压缩应变。
当管道局部弯曲时,中性面一侧将发生压缩变形,当管壁最大压应变达到或超过临界应变时,管壁会出现局部屈曲或褶皱。为了防止压缩变形引起的管道失效,对压缩应变提出了以下要求[3]:
| $ {\varepsilon _{{\rm{cf}}}} \le {\varphi _{{\rm{ \mathit{ ε} c}}}}\varepsilon _{\rm{c}}^{{\rm{crit}}}, $ | (23) |
式中:εcf为因子化的纵向或环向压缩应变,无量纲;φεc为压缩应变阻力因子,无量纲,可取0.8;εccrit为管道的纵向或环向压缩极限应变,无量纲,通常由实验确定,且应考虑内压、外压、初始缺陷、残余应力和材料本构关系等因素的影响,缺乏具体信息时按式(24)取值。
| $ \varepsilon _{\rm{c}}^{{\rm{crit}}} = \left\{ \begin{array}{l} 0.5\frac{t}{D} - 0.0025 + 3000{\left( {\frac{{\left( {{p_{\rm{i}}} - {p_{\rm{e}}}} \right)D}}{{2tE}}} \right)^2}, \frac{{\left( {{p_{\rm{i}}} - {p_{\rm{e}}}} \right)D}}{{2t{\sigma _{\rm{S}}}}} < 0.4;\\ 0.5\frac{t}{D} - 0.0025 + 3000{\left( {\frac{{0.4{\sigma _{\rm{S}}}}}{E}} \right)^2}, \frac{{\left( {{p_{\rm{i}}} - {p_{\rm{e}}}} \right)D}}{{2t{\sigma _{\rm{S}}}}} \ge 0.4。\end{array} \right. $ | (24) |
式中:t为管道壁厚,mm;D为管道外径,mm;pi为为最大设计内压,MPa;pe为为最小外部静水压力,MPa;E为弹性模量,MPa;σS为屈服强度,MPa。
以兰成渝输油管道某管段为例,外径D=508 mm,壁厚t=8.6 mm,设计压力pi=10 MPa,pe≈0,E=2.07×10-5 MPa,σS=410 MPa,代入公式(24),得εccrit=0.007 8,代入式(23),得压缩应变临界值为0.624%。由于管线钢压缩变形多由忽然载荷引起,且呈现局部性,细长管道悬空时的压缩变形还将引起失稳。为安全起见,此处仍沿用式(23)、式(24)作为压缩变形的失效判据。
2) 椭圆化变形。
当管道受到外部挤压载荷时,管道横截面可能出现椭圆化变形。管道横截面形状的改变会导致内检测器无法通过,影响管道使用。椭圆化变形率Δθ定义[3, 17]为
| $ {\Delta _\theta } = 2\left( {{D_{\max }} - {D_{\min }}} \right)/\left( {{D_{\max }} + {D_{\min }}} \right), $ | (25) |
式中:Dmax和Dmin分别为管道的最大和最小外径,mm。
文献[3]对管道椭圆化变形的要求为
| $ {\Delta _\theta } \le {\Delta _{\theta {\rm{crit}}}}, $ | (26) |
式中:Δθcrit为临界椭圆化变形率,通常通过分析或实验确定,或取0.03[3, 17]。
笔者未对椭圆化变形的失效判据进行详尽的分析研究,此处仍沿用公式(25)作为椭圆化变形的失效判据。
4 结论1) 通过研究X60管线钢的单向拉伸实验曲线和Ramberg-Osgood本构模型,发现ε≤εP0.2时,Ramberg-Osgood本构方程能够准确地反映X60管线钢的拉伸应力应变关系,但当ε>εP0.2时,基于Ramberg-Osgood本构模型所得理论本构曲线与实验曲线有较大的误差。笔者对Ramberg-Osgood本构模型做出了修正,建立了与实验结果相吻合的全局二段式本构方程。
2) 研究了X60管线钢基于应力的失效判据,建立了基于第四强度理论的管道失效时的临界应力计算方程。
3) 研究了X60管线钢基于应力的失效判据和基于应变的失效判据,提出了在管道输送工程中应该采用的应力控制失效准则和应变控制失效准则。
| [1] |
罗敏, 马学峰, 刘军, 等.
川渝天然气管道工程建设发展情况及建议[J]. 天然气工业, 2006, 26(3): 107–110.
LUO Min, MA Xuefeng, LIU Jun, et al. The development situation and suggestions of natural gas pipeline engineering in Sichuan and Chongqing[J]. Natural Gas Industry, 2006, 26(3): 107–110. (in Chinese) |
| [2] |
曾亚武, 黎玲, 熊俊, 等.
基于塑性体积应变的梯度塑性理论研究[J]. 长江科学院院报, 2012, 29(8): 7–11.
ZENG Yawu, LI Ling, XIONG Jun, et al. Gradient Plasticity Theory Based on Plastic Bulk Strain[J]. Journal of Yangtze River Scientific Research Institute, 2012, 29(8): 7–11. (in Chinese) |
| [3] | 帅健. 管线力学[M]. 北京: 科学出版社, 2010. |
| [4] |
王元清, 常婷, 石永久, 等.
奥氏体不锈钢S31608的本构关系试验[J]. 清华大学学报:自然科学版, 2013(9): 1231–1234.
WANG Yuanqing, CHANG Ting, SHI Yongjiu, et al. Experimental study of the stress-strain relation of austenitic stainless steel S31608[J]. Journal of Tsinghua University:Science and Technology, 2013(9): 1231–1234. (in Chinese) |
| [5] | Shinohara Y, Hara T, Tsuru E. Development of a high strength steel line pipe for strain-based design applications[C]//Proceedings of the 17th International Offshore and Polar Engineering Conference, July 1-6, 2007, Lisbon, Portugal.Cupertino:The International Society of Offshore and Polar Engineers, 2007. https://www.researchgate.net/publication/283412347_Development_of_a_high_strength_steel_line_pipe_for_strain-based_design_applications |
| [6] |
李璞, 陶燕丽, 周建.
基于应变设计管道局部屈曲应变极限值的计算[J]. 天然气工业, 2013, 33(7): 101–107.
LI Pu, TAO Yanli, ZHOU Jian. A study of the ultimate compressive strain of local buckling in strain-based design of pipelines[J]. Natural Gas Industry, 2013, 33(7): 101–107. DOI:10.3787/j.issn.1000-0976.2013.07.018 (in Chinese) |
| [7] | Jiang Y R, Chen M B. Research on the fatigue fracture surface of X60 pipeline steel after per-tension deformation[J]. Advanced Materials Research, 2012, 487: 423–426. DOI:10.4028/www.scientific.net/AMR.487 |
| [8] |
刘冰, 刘学杰, 张宏.
基于应变的管道设计准则[J]. 天然气工业, 2008, 28(2): 129–131.
LIU Bing, LIU Xuejie, ZHANG Hong. Lriteria for the design of the pipeline based on strain[J]. Natural Gas Industry, 2008, 28(2): 129–131. (in Chinese) |
| [9] |
马廷霞, 吴锦强, 唐愚, 等.
成品油管道的极限悬空长度研究[J]. 西南石油大学学报, 2012, 34(4): 165–173.
MA Tingxia, WU Jinqiang, TANG Yu, et al. Maximum suspended length ofproduction pipeline[J]. Journal of Southwest Petroleum University, 2012, 34(4): 165–173. (in Chinese) |
| [10] |
朱浩川, 姚谏.
不锈钢材料的应力应变模型[J]. 空间结构, 2011, 17(1): 62–69.
ZHU Haochuan, YAO jian. Stress-strain model for stainless steel[J]. Spatial Structures, 2011, 17(1): 62–69. (in Chinese) |
| [11] |
郑宝锋, 舒赣平, 沈晓明.
不锈钢材料常温力学性能试验研究[J]. 钢结构, 2011, 5(26): 1–6.
ZHENG Baofeng, SHU Ganping, SHEN Xiaoming. Eeperimental study on material properties of stainless steel at room temperature[J]. Steel Construction, 2011, 5(26): 1–6. (in Chinese) |
| [12] | Hara T, Shinohara Y, Hattori Y, et al. Development and mass production of X60 high deformable line pipe suitable for strain-based design[C]//Proceedings of the Twenty-first International Offshore and Polar Engineering Conference, June 19-24, 2011, Maui, Hawaii, USA. Cupertino:International Society of Offshore and Polar Engineers, 2011. https://www.researchgate.net/publication/286725944_Development_and_mass_production_of_X60_high_deformable_line_pipe_suitable_for_strain-based_design |
| [13] | 王志文, 蔡仁良. 化工容器设计[M]. 3版. 北京: 化学工业出版社, 2005. |
| [14] | Song B, Cheng J J R, Chan D H, Zhou J. Numerical simulation of stress relief of buried pipeline at Pembina river crossing[C]//Proceedings of the ASME International Pipeline Conference 2006. New York, United States, ASME, 2007. https://www.researchgate.net/publication/267644102_Numerical_Simulation_of_Stress_Relief_of_Buried_Pipeline_at_Pembina_River_Crossing |
| [15] | 薛守义. 弹塑性力学[M]. 北京: 中国建材工业出版社, 2005. |
| [16] |
张京海, 方大鹏.
高强钢低匹配焊接接头应用性能研究[J]. 材料开发与应用, 2012(3): 1–6.
ZHANG Jinghai, FANG Dapeng. Practicability research on low-match weld joint of high-strength steel[J]. Development and Application of Materials, 2012(3): 1–6. (in Chinese) |
| [17] |
张九菊, 段梦兰, 马建敏, 等.
基于深海卷管铺设的海管椭圆度分析[J]. 应用数学和力学, 2013, 34(6): 552–563.
ZHANG Jiuju, DUAN Menglan, MA Jianmin, et al. Study on ovalization of submarine pipe during deep water reel-lay[J]. Applied Mathematics and Mechanics, 2013, 34(6): 552–563. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

