图像分割是一种基本的计算机视觉技术,也是由图像处理进入到图像分析的关键步骤,一直是数字图像处理领域的一项重要研究内容。图像分割不仅要求快速,而且要准确地分割图像。一直以来都是图像处理领域中的一个经典难题,目前还没有某个算法能令人满意地分割各种特征的图像[1],往往需要基于图像类型人们主观地选择分割方法,这其中基于模型和基于区域的分割方法是比较常用的分割方法。
基于模型的图像分割方法可以分为两种[2]:一种是基于水平集方法的几何活动轮廓模型,由Osher和Sethian[3]提出;另一种是基于变分方法的参数活动轮廓模型,其代表为主动轮廓模型分割算法,主要由Kass等人[4]提出。相对于传统的图像分割方法,基于模型的图像分割方法分割速度较快,实用性较强,因而得到了广泛的应用[5-8]。而在此基础之上,Chan等[9]提出了基于变形曲线、Mumford-Shah分割函数和水平集的Chan-Vese模型[10]。Chan-Vese模型的最大缺点就是演化速度很慢,尤其是对目标和背景灰度差较小的图像[11-12],而且,其处理直线和尖角的能力也较弱。
笔者在研究分析Chan-Vese模型的基础之上,发现其演化速度慢的原因,然后提出一种结合阈值分割方法的Chan-Vese模型分割方法。
1 Chan-Vese模型Chan-Vese模型属于单水平集二相分割算法,首先给出其定义。与实数c对应的可微函数f的水平集是实点集{(x1,x2,…,xn)|f(x1,x2,…,xn)=c},称可微函数f为水平集函数。令Ω为R2的有界开子集,φ:Ω→R为Lipschitz连续的水平集函数。轮廓曲线Γ
| $ \left\{ \begin{align} & \mathit{\Gamma =}\left\{ \left( x, y \right)\left| \left( x, y \right)\in \mathit{\Omega },\varphi \left( x, y \right)=0 \right. \right\}, \\ & {{\omega }_{\text{1}}}\mathit{=}\left\{ \left( x, y \right)\left| \left( x, y \right)\in \mathit{\Omega },\varphi \left( x, y \right)>0 \right. \right\}, \\ & {{\omega }_{2}}\mathit{=}\left\{ \left( x, y \right)\left| \left( x, y \right)\in \mathit{\Omega },\varphi \left( x, y \right)<0 \right. \right\}。\\ \end{align} \right. $ | (1) |
令u:Ω→R,Ω
| $ \begin{align} & F\left( {{c}_{1}}, {{c}_{2}}, \varphi \right)\mathit{=}\mu \int\limits_{\mathit{\Omega }}{\left| \nabla H\left( \varphi \left( x, y \right) \right) \right|}\text{d}x\text{d}y+\nu \int\limits_{\mathit{\Omega }}{\left| H\left( \varphi \left( x, y \right) \right) \right|}\text{d}x\text{d}y \\ & +{{\lambda }_{1}}{{\int\limits_{\mathit{\Omega }}{\left| \mu \left( x, y \right)\text{-}{{c}_{1}} \right|}^{2}}}H\left( \varphi \left( x, y \right) \right)\text{d}x\text{d}y+{{\lambda }_{2}}{{\int\limits_{\mathit{\Omega }}{\left| \mu \left( x, y \right)\text{-}{{c}_{2}} \right|}^{2}}}\left( 1\text{-}H\left( \varphi \left( x, y \right) \right) \right)\text{d}x\text{d}y, \\ \end{align} $ | (2) |
式中:H为单位阶跃函数;μ≥0,ν≥0,λ1>0,λ2>0为固定系数;c1和c2为曲线Γ内外平均灰度,分别表示为
| $ {{c}_{1}}\left( \varphi \right)\text{=}\frac{\int\limits_{\mathit{\Omega }}{\mu \left( x, y \right)H\left( \varphi \left( x, y \right) \right)\text{d}x\text{d}y}}{\int\limits_{\mathit{\Omega }}{H\left( \varphi \left( x, y \right) \right)\text{d}x\text{d}y}}, $ | (3) |
| $ {{c}_{2}}\left( \varphi \right)\text{=}\frac{\int\limits_{\mathit{\Omega }}{\mu \left( x, y \right)\left( 1\text{-}H\left( \varphi \left( x, y \right) \right) \right)\text{d}x\text{d}y}}{\int\limits_{\mathit{\Omega }}{\left( 1\text{-}H\left( \varphi \left( x, y \right) \right) \right)\text{d}x\text{d}y}}。$ | (4) |
能量函数是变分分割模型,该函数是由具有一定物理意义的正则化项构成。当能量函数取到最小值时,分割轮廓收敛于图像真实边界处。能量函数最小值的求解一般通过一阶变分来实现。因为能量函数的一阶变分为0,是能量函数取最小值的必要条件。
对能量函数(2)求一阶变分,可以导出如下Euler-Lagrange方程:
| $ \frac{\partial \varphi }{\partial t}=\delta \left( \varphi \right)\left[\mu \text{div}\left( \frac{\nabla \varphi }{\left| \nabla \varphi \right|} \right)-\nu-{{\lambda }_{1}}{{\left( u-{{c}_{1}} \right)}^{2}}+{{\lambda }_{2}}{{\left( u-{{c}_{2}} \right)}^{2}} \right]。$ | (5) |
解方程(5)求得φ,就可以得到二区域分割结果为
| $ \left\{ \begin{align} & {{\bf{R}}_{1}}=uH\left( \varphi \right), \\ & {{\bf{R}}_{2}}=u\left( 1-H\left( \varphi \right) \right)。\\ \end{align} \right. $ | (6) |
根据式(5)可以做进一步的分析,方程的右端是各项对演化起到限制作用的因子。第一项对应的是曲线的长度因子,第二项是曲线包围的面积因子。对式(5)进行差分求解时,曲线的长度和面积都是在不断减小的,最终得到光滑曲线。系数μ,ν是尺度系数,当其值较大时只有较大的目标物体能被检测到,当其值较小时较小的目标物体也能被检测到,并且系数的正确选择有助于去除噪声。对于右端的第三项,假定λ1=λ2=1,因为-(I-c1)2+(I-c2)2=2(c1-c2)
如果能预先对图像进行处理、变换,拉伸灰度级范围,加大演化曲线内外灰度值差c1-c2,这样就会保持较高的水平集演化速度。基于以上分析,提出如下改进方案:
首先对待处理图像进行基于灰度直方图的阈值分割,阈值分割方法基于对灰度图像的一种假设:目标或背景内相邻像素间的灰度值是相似的,但不同目标或背景的像素在灰度上有差异,反映在图像直方图上,不同目标和背景则对应不同的峰。最简单的阈值选取方法就是选取位于两个峰之间的谷,从而将各个峰分开。阈值分割的优点是实现简单,对于不同类的物体灰度值或其他特征值相差很大时,它能很有效地对图像进行分割。
由于此处需要的并不是简单的用阈值方法来分割图像,而是要利用双阈值排除掉背景和目标区域内大部分过高或者过低灰度值的像素,通过尺度变换加强目标边缘处的灰度值差,因此,选择两个峰处为双阈值进行阈值分割。
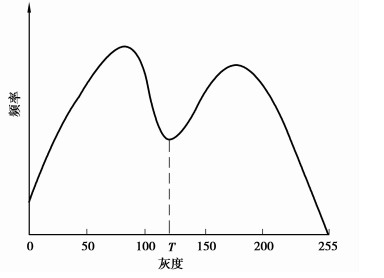
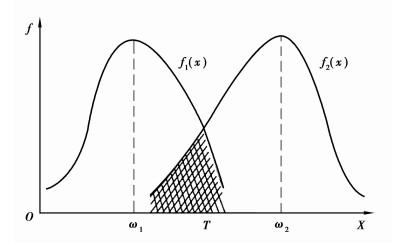
因为未进行阈值分割前,原图像全部像素点的灰度值范围为0~255,见图 1,分割后的图像全部像素点的灰度值范围为ω1~ω2(0 < ω1 < ω2 < 255),见图 2,对像素灰度值范围为ω1~ω2的图像进行灰度值尺度变换,变换公式为
| $ G\left( z \right)=\frac{{{g}_{\text{m}}}}{{{\omega }_{2}}-{{\omega }_{1}}}\left( z-{{\omega }_{1}} \right), \left( {{\omega }_{1}} < z < {{\omega }_{2}} \right)。$ | (7) |
|
图 1 图像灰度分布频率图 |
|
图 2 双阈值的选取 |
其中z为图像灰度值,灰度最大值为gm(一般gm为255),G(z)为尺度变换后原像素点新灰度值。通过灰度值尺度变换,将经过阈值分割后灰度值范围为ω1~ω2的图像的灰度值范围重新变换为0~255,这样就实现了图像灰度值范围的拉伸,在实际处理中还可以根据具体情况调整阈值的选取,控制放缩的幅度。
从而可将Chan-Vese模型改进为
| $ \begin{align} &{{E}_{\text{new}}}\left( {{c}_{1}},{{c}_{2}},\varphi \right)=\mu \int\limits_{\mathit{\Omega }}{\left| \nabla H\left( \varphi \left( x,y \right) \right) \right|}\text{d}x\text{d}y+\nu \int\limits_{\mathit{\Omega }}{\left| H\left( \varphi \left( x,y \right) \right) \right|}\text{d}x\text{d}y \\ &+{{\lambda }_{1}}\int\limits_{\mathit{\Omega }}{{{\left| \mu \left( x,y \right)\text{-}{{c}_{1}} \right|}^{2}}}H\left( \varphi \left( x,y \right) \right)\text{d}x\text{d}y+{{\lambda }_{2}}\int\limits_{\mathit{\Omega }}{{{\left| \mu \left( x,y \right)\text{-}{{c}_{2}} \right|}^{2}}}\left( 1\text{-}H\left( \varphi \left( x,y \right) \right) \right)\text{d}x\text{d}y。\\ \end{align} $ | (8) |
最小化能量函数Enew(φ),就能以迭代的方式得到如下求解φ的Euler-Lagrange方程:
| $ \left\{ \begin{array}{l} \frac{{\partial \varphi }}{{\partial t}} = \delta \left( \varphi \right)\left[ \begin{array}{l} \mu {\text{div}}\left( {\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}}} \right) - \nu ,\\ - {\lambda _1}{\left( {G\left( z \right) - {c_1}} \right)^2} + {\lambda _2}{\left( {G\left( z \right) - {c_2}} \right)^2} \end{array} \right],\\ \varphi \left( {t,x,y} \right) = {\varphi _0}\left( {x,y} \right),\\ \frac{{\delta \left( \varphi \right)\partial \varphi }}{{\left| {\nabla \varphi } \right|\partial n}} = 0,\\ \frac{{\partial \varphi }}{{\partial t}} = \frac{{{\varphi ^{n + 1}} - {\varphi ^n}}}{{\Delta t}}。\end{array} \right. $ | (9) |
式中:t为时间变量;φ为水平集函数,当t=tn时,用φn表示当前的水平集φ。Chan-Vese模型的具体算法如下:
① 令n=0,初始化φ0;
② 用式(3)、式(4)计算c1(φn)和c2(φn),且当p=2时,有length{φn=0}=L(φn);
③ 用式(9)计算φn的偏微分方程,从而进一步求出φn+1;
④ 检查φn+1是否为稳态解,若不是则n=n+1,跳入②再次循环。
3 实验结果及讨论为验证提出算法的有效性,在运行Windows 7的实验平台(Intel Core i5四核2.80 GHz/内存4G)进行了仿真验证,程序用Matlab R2011a编写。
实验模型参数取值:μ=0.001×2552,ν=0,λ1=λ2=1,Δt=0.1 s。
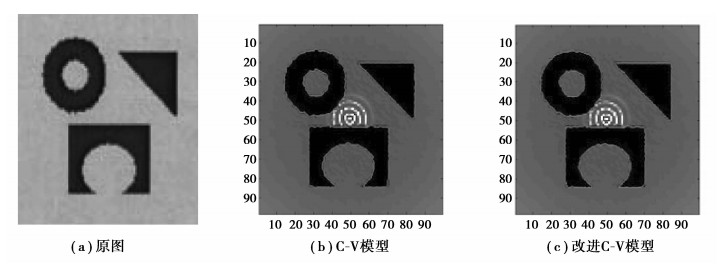
图 3是一组简单的几何图形,是一张二值图像,主要目的是验证算法的可行性,结果表明:Chan-Vese算法和改进C-V算法都能很好地分割出图像。
|
图 3 两种算法分割简单几何图像 |
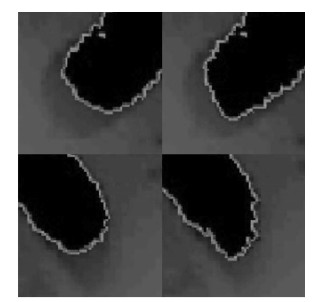
从图中脑室CT图像分割结果(图 4)来看,Chan-Vese模型分割方法在灰度值变化剧烈时能量最小化效果显著,能够准确判断并继续演化,但是在灰度变化缓和时,能量函数对停止收敛的判断存在很大的不确定性,导致最终分割过早结束,产生不完全分割的结果。而笔者提出的方法则大大改善了原方法这一缺陷,在腰部及右下尖锐边缘处很好地跟踪捕捉到了目标边缘,扩大了分割结果的有效面积。另一方面,Chan-Vese模型的最优化结果需要对整张图像素点的遍历,导致算法需要花费大量时间。笔者引入阈值算法预分割,阈值分割初步地排除掉大部分干扰算法分割,缩小算法遍历定义域,在进一步的Chan-Vese模型分割时大大减少了遍历的像素点,再结合尺度变化后保证了水平集的演化速度,最终达到了节省大量分割时间的目的。从图 5中可看出改进C-V算法的有效面积明显增大,图 6反映了改进C-V算法对复杂边缘良好的追踪。

|
图 4 两种算法对图像分割结果 |
|
图 5 局部分割效果放大后对比 (左为C-V模型,右为改进C-V模型) |
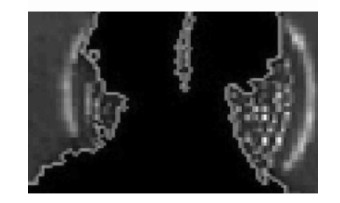
|
图 6 改进算法对尖锐边缘分割效果 |
在验证实验中,选择了对比度较低、边缘异常不规则的图像(图 7),传统C-V模型的需要更多迭代次数,导致分割时间增加,而尖锐的边缘使其分割有效面积更小。改进的C-V模型则在一定程度上弥补了传统C-V模型算法分割的不足,如图 8所示。
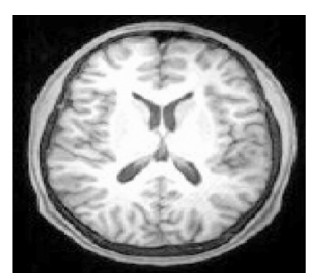
|
图 7 脑室PET图像 |
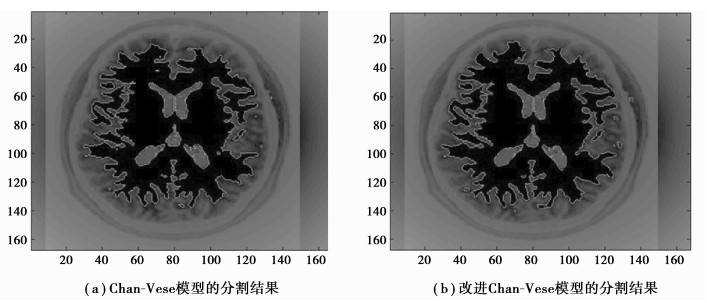
|
图 8 两个分割算法对比 |
在第一组实验中,C-V模型耗时2.66 s,改进算法耗时2.03 s,有效面积增大率为3.5%;第二组实验中,C-V模型耗时3.87 s,改进算法耗时2.96 s,有效面积增大率为4.7%。实验表明:结合阈值算法的Chan-Vese模型图像分割方法提高了图像分割的准确性和快速性。
4 结语笔者利用阈值分割算法和C-V模型图像分割算法相结合的方式,充分发挥阈值分割方法简单快速和Chan-Vese模型自动化程度高,分割准确的优点,大大节省了算法分割图像时间的同时,有效优化了C-V模型处理复杂图像的能力,并通过实验验证了该方法的有效性和合理性,实现了预定目标,对临床医学具有实际的意义。
| [1] |
罗希平, 田捷, 诸葛婴, 等.
图像分割方法综述[J]. 模式识别与人工智能, 1999, 12(3): 300–312.
LUO Xiping, TIAN Jie, ZHU Geying, et al. Method of image segmentation[J]. Pattern Recognition and Artificial Intelligence, 1999, 12(3): 300–312. (in Chinese) |
| [2] | 郑南宁. 计算机视觉与模式识别[M]. 北京: 国防工业出版社, 1998. |
| [3] | Osher S, Sethian J A. Fronts prop-agating with curvature-dependent speed:algorithms based on Hamil-ton-Jacobi formulation[J]. Jour-nal of Computation Physics, 1988, 79: 12–49. DOI:10.1016/0021-9991(88)90002-2 |
| [4] | Kass M, Witkin A, Terzopoulos D. Snakes:active contour models[J]. International Journal of Computer Vision, 1987, 1(4): 321–331. |
| [5] | Morar A, Moldoveanu F, Groller E. Image segmentation based on active contours without edges[J]. Intelligent Computer Communication and Processing, 2012: 213–220. |
| [6] | Lee S H, Seo J K. Level set-based bimodal segmentation with statio-nary global minimum[J]. IEEE Tran-sactions on Image Processing, 2006, 15(9): 2843–2852. DOI:10.1109/TIP.2006.877308 |
| [7] | Li C, Kao C, Gore J C, et al. Minim-ization of region-scalable fitti-ng energy for image segmentati-on[J]. IEEE Transactions on Image Processing, 2008, 17(10): 1940–1949. DOI:10.1109/TIP.2008.2002304 |
| [8] | Wang L, Li C, Sun Q, et al. Active contours driven by local and glo-bal intensity fitting energywith application to brain MR image segmentation[J]. Computerized Medical Imaging and Graphics, 2009, 33: 520–531. DOI:10.1016/j.compmedimag.2009.04.010 |
| [9] | Chan T F, Vese L A. Active cont-ours without edges[J]. IEEE Tran-sactions on Image Processing, 2001, 10(2): 266–277. DOI:10.1109/83.902291 |
| [10] | Wang X, Huang D, Xu H. An efficient local Chan-Vese model for image segmentation[J]. Pattern Recogn-ition, 2010, 43(3): 603–618. DOI:10.1016/j.patcog.2009.08.002 |
| [11] |
原野, 何传江.
LBF活动轮廓模型的改进[J]. 计算机工程与应用, 2009, 45(15): 177–179.
YUAN Ye, HE Chuanjiang. Improvement of LBF active contours model[J]. Computer Engineering and Applications, 2009, 45(15): 177–179. DOI:10.3778/j.issn.1002-8331.2009.15.051 (in Chinese) |
| [12] | 高佳. 医学图像分割与三维重构研究[D]. 兰州: 兰州大学, 2010. http://d.wanfangdata.com.cn/Thesis/Y1702760 |
 2014, Vol. 37
2014, Vol. 37


