1b. 成都信息工程学院 网络工程学院, 成都 610225;
2. 电子科技大学 互联网科学中心, 成都 610054
1b. College of Network Engineering, Chengdu University of Information Technology, Chengdu 610225, China;
2. Web Science Center, University of Electronic Science and Technology of China, Chengdu 610054, China
在复杂网络的研究中,疾病与舆情的传播动力学是其中的一个热点[1]。针对网络结构特点,提出有效的免疫策略,以及比较不同免疫策略的效果,都是复杂网络免疫研究的重要内容。根据网络结构可以将复杂网络分为两类:一是均匀网络[2-3],另一类是无标度网络[4]。人们根据网络的结构特征提出了较多的免疫策略,目前比较常见的3种免疫策略:随机免疫[5-6];即在网络中随机选择节点进行免疫;目标免疫[7],即在网络中选择度数最大的顶点进行免疫(为了便于区别,将这里的随机免疫称为全网络的随机免疫、目标免疫称为全网络的目标免疫);熟人免疫[8],即首先随机选择一个节点,再随机选择一个与该节点相邻的节点进行免疫。其他的免疫策略,如“比例优先免疫”策略[9],即每个节点被免疫的概率与该节点的度数成正比,以及由Hayashi提出的,如果要想控制疾病传播,就必须控制种群数量的增长的策略[10],等等。其中随机免疫对均匀网络比较有效,而目标免疫则比较适合于无标度网络。笔者提出了一种新的免疫策略:对独立集[11]中度数最大的顶点进行免疫的方法。
随着计算机技术和图论的发展,对顶点数目众多的复杂网络的顶点进行正常着色[11]已经没有问题,当对复杂网络的顶点进行正常的着色(提及的着色都是正常的着色)后,着相同颜色顶点构成的集合就是网络顶点的独立集[11]。至今很少有人将独立集应用于复杂网络的研究[12-13],仅有的将独立集应用于复杂网络免疫研究的是随机免疫[12],而非目标免疫。目前的研究结论是目标免疫更适用于无标度网络。本文基于独立集中任意两个顶点均不相邻的特点提出了一种免疫策略:免疫独立集中度数最大的节点,我们将其称为独立集的目标免疫。将这一免疫策略应用于BA网络模型,并对实验结果进行了分析。同时对独立集的随机免疫策略[12]进行了更深入地研究,在比较了独立集的随机免疫策略与全网络的随机免疫时,独立集的随机免疫策略效果更好,发现这2种免疫方法所免疫的节点的总度数和十分接近。由于SI传播模型的节点只有2种状态,S态和I态。在研究基于网络结构的免疫策略时,使用这种传播模型比使用SIR、SIS将更加有利。
1 着色算法及传播模型的选择着色是图论中的一个重要部分,在“四色问题”被提出来的一百多年间[11],着色的理论和应用得到极大的发展。在众多的着色算法中,如果选择“回溯时序”这样的着色算法[14],时间复杂度太高,无法对顶点数目很大的复杂网络着色;但选择“贪婪算法”[15],虽然时间复杂度不高,能够对顶点数目很大的复杂网络着色,但所用颜色数目比“最大度优先的Welsh-Powell点着色算法”[11, 16]多,因此选择的是能够对规模巨大的复杂网络顶点进行着色且所用颜色数目较少的“最大度优先的Welsh-Powell点着色算法”,算法的时间复杂度是O(N2)[17](N表示图的顶点数目)。此算法具体步骤如下
给定网络G=(V,E),V,E,代表网络的顶点和边的集合,设V={v1,v2,…,vn},着色函数为π,色集C={1,2,…,Δ+1},Δ代表图G的最大度。
步骤1 k(v1)≥k(v2)≥…≥k(vn);
步骤2 令π(v1)=1,i=1;
步骤3 若i=n,则停;否则令C(vi+1)={π(vj)|j≤i,并且vj与vi+1相邻},设m为C\C(vi+1)中的最小正整数(其中C\C(vi+1)的意思是集合C减去集合C(vi+1)),令π(vi+1)=m;
步骤4 令i=i+1,转步骤3。
在以上着色算法中,k(vi)代表顶点vi的度数;C代表色集;π(vi)=m表示顶点vi着m色。
当对复杂网络的顶点进行正常着色后,着相同颜色的顶点构成的集合即是独立集,此集合中的顶点具有任意2个顶点均不相邻的特点。
SI、SIR和SIS是在传染病动力学中常用的3种传播模型,现在被广泛的应用到复杂网络的传播动力学研究当中[18]。这3种传播模型最初的意思是:SI模型:患病后难以治愈[19];SIS模型:患病后可以治愈[19];SIR模型:患病治愈后获得了终身免疫力[19]。目前复杂网络传播动力学的研究结论是网络结构在传播的过程中起着决定性的作用,当研究一种免疫策略是基于网络结构做出的,用SI传播模型将更加有利。因为使用SIR传播模型时,I态节点在一个时间步后,将会成为R态节点,而此时R态节点的作用与免疫节点的作用是相同,不能被感染,也不能传播疾病,因此从网络结构上进行免疫的研究,使用SI传播模型更好,更能够体现免疫策略的真实效果。用SIS传播模型做免疫研究时与SIR模型有类似的情况,因此选择SI传播模型进行免疫策略研究,所有实验都使用SI传播模型。
2 独立集的免疫策略在选定了着色算法对复杂网络顶点进行正常着色后,将着相同颜色的顶点归为一个集合,就可以得到网络的独立集。基于独立集的免疫策略是免疫一个独立集中的部分或全部节点,由于独立集中任意2个顶点均不相邻,免疫独立集中的节点可以达到更加广泛地免疫网络中的节点的目的。
2.1 对独立集中度数最大节点的免疫策略现实世界的许多网络的度分布函数具有幂率形式,为解释幂率分布的产生机理,Barabasi和Albert于1999年在Science发表的论文中提出了一个无标度网络模型,又称为(Barabasi-Albert)BA网络模型[4]。无标度网络对于目标攻击极具脆弱性[20],在比较全网络的目标免疫与免疫一个独立集中最高度数节点的实验中,当两种免疫方法免疫节点数目相同时,传播模型无论是SIR还是SI,其结果仍然是全网络目标免疫的效果好,这与以往的结论是吻合的[20]。提出的新免疫方法是在独立集中免疫度数最高的一些节点(节点度数按降序排列,以节点度数从高到低的方法免疫)计算出免疫节点的总度数和再在全网络中免疫一定数量的节点,要求这些节点的度数在全网络中相比较是最大的(同样节点度数按降序排列,按节点度数从高到低的方法免疫),同时这些节点的总度数和等于在独立集中免疫节点的度数和。这2种方法可以简单称为:一个是全网络的目标免疫,另一个是独立集中的目标免疫,要求免疫节点总度数和相等。
在网络模型的选择上,使用的是BA网络模型,网络顶点数目为10 000,初始时m0=3,每一时间步添加的边的数目m=2,网络平均度〈k〉=4,在实验中,为了便于比较,所有BA网络模型参数都相同。在对此网络模型的顶点进行正常着色后,本质上是对网络模型的顶点进行了划分,让着相同颜色的顶点分在同一个集合里。又因为进行的是正常着色,着相同颜色的顶点均不相邻,最终网络模型的顶点被分成几个的独立集。传播模型选择的是SI传播模型,节点之间采用全接触的传播模式,传播率为:0.1,所有实验都是是50次的平均。
下面的实验是免疫第一大独立集(第一大独立集是独立集中顶点数目最多的独立集)中部分节点的结果。在图 1中,IN代表免疫第一大独立集中的度数最大的部分节点,设这些免疫节点的度数和为“SUM”;AN是在整个网络中免疫度数最高的节点,并且这些免疫节点的度数和等于第一大独立集中免疫节点的度数和“SUM”。对网络进行了免疫后,再在网络中随机感染10个节点作为传播源,比较这2种免疫方式对传播的影响。在传播平衡时,I态节点数目越少表示免疫的效果越好。
|
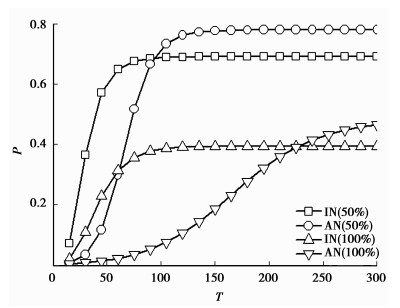
图 1 在BA网络模型中免疫第一大独立集中50%、100%的节点,横轴:传播时间;纵轴:传播时I态粒子个数占整个网络节点数目的比例。 |
由于BA网络模型对目标攻击是十分脆弱的[20]。当在整个网络中去掉度数最大的节点时,对网络的连通性破坏很大[20],因此免疫整个网络中度数最高的节点的方法,在初期的传播速度很慢。在以独立集方法免疫时最初一旦有较高度数节点被感染(这种可能性很大,因为在没有进行免疫的其他独立集中,仍然有高度数节点),此时独立集免疫方法在网络中的传播速度很快,参看图 1。大约在90个时间步后,以独立集免疫方法就基本达到平衡,即在很短的时间内,它能够传播多远、多广就确定了,主要原因有2个:一是独立集免疫策略使网络的最大连通分支的规模更小,规模小时传播就更快;二是有些分支中存在度数较大的节点,节点的度越大越有利于传播;对于这两个原因在图 2、图 3的实验都有说明。全网络的目标免疫策略,要用比它多得多的时间才能达到平衡。在整个网络中免疫度数最高的节点时,免疫后最大连通分支的节点数目更多,加之高度数节点被免疫掉(最大连通分支的高度数节点更少),传播进行得相对缓慢;但随着时间的增加,全网络的免疫策略使网络中感染节点的数目都多过独立集免疫策略(见图 1),主要原因在于全网络的免疫,使网络的最大连通分支更大,能被感染的节点更多。对于全网络的目标免疫策略使网络的“最大连通分支更大”和“最大连通分支的高度数节点更少”的结论在后面图 2、图 3的实验中也有说明。图 1的实验说明独立集的目标免疫策略更好,因为最终是独立集的免疫策略,让网络中受感染的节点数目更少。图 1的实验是免疫第一大独立集中50%、100%的节点,对于免疫第一大独立集中25%和75%的节点有类似的结果;如果免疫网络中其他独立集的节点与第一大独立集也有完全类似的结论,这里没有一一画出。
|
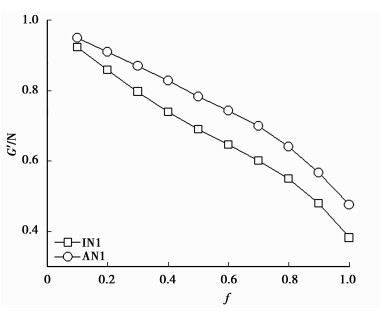
图 2 BA网络模型,对第一大独立集鲁棒性实验,横轴:免疫独立集中最大度节点比例,纵轴:最大连通子图节点占整个网络节点的比例。 |
|
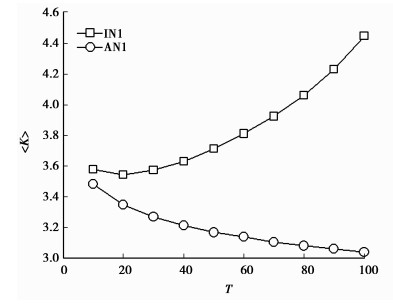
图 3 BA网络模型,最大连通子图的平均度。横轴的数值表示免疫第一大独立集中最大度节点比例,纵轴:最大连通子图的平均度数。 |
这2种免疫方式(独立集和全网络的免疫),要求免疫节点总的度数相等,等价于在网络中免疫数目相同的边。这一实验也说明:如果要对网络的边进行免疫,在免疫一定数目边时,选择同一独立集中的边(从顶点度数最大的点开始)比选择网络中度数最大节点相关联的边,免疫效果更好。
下面的2个实验从网络结构上对图 1的实验结果进行解释,对网络顶点免疫,等同于在网络中去掉免疫节点和免疫节点相关联的边。
图 2是对以上2种免疫策略网络鲁棒性的研究。横轴表示免疫第一大独立集中节点的百分比(从10%到100%),纵轴表示免疫后网络中最大连通子图的节点数占整个网络总节点数目的比例。IN1代表免疫第一大独立集中度数最大的一定比例的节点;AN1代表免疫全网络中度数最大的节点,要求免疫节点的总度数和等于独立集中免疫节点度数和。实验结果表明,在免疫最大度节点总度数和相等的条件下,对独立集的目标免疫与全网络目标免疫相比较,独立集的免疫策略使网络最大连通子图更小,即独立集的目标免疫策略使网络受到更大的破坏,这也是对独立集的免疫比在全网络中进行免疫效果更好的原因。其中独立集中的节点肯定不相邻,确保所选择的节点在整个网络中更加分散,因此对独立集中的节点的免疫使网络更加破碎,这验证了前面提出的“独立集免疫策略使网络的最大连通分支的规模更小”的观点。对于其他独立集的实验有相似的结论,这里没有一一画出。
下面的实验同样是免疫独立集和全网络中最大度节点、节点总度数和相等,检验免疫后网络最大连通子图的平均度。得到对独立集免疫时,最大连通子图的平均度增加,而对全网络免疫时,最大连通子图的平均度减少。在图 3中,IN1是免疫第一大独立集中一定比例的最大度节点,并统计这些节点的度之和,设为“SUM”;AN1是免疫整个网络中,一定数量度数最大的节点,使这些节点的度之和等于“SUM”。
免疫独立集中度数最大的节点使网络的最大连通子图仍然保留下度数较高的节点,因此最大连通子图的平均度更高;而全网络的最大度免疫策略,使网络中最大连通子图的高度数节点数目迅速减少,导致最大连通子图的平均度更低,即连通子图的高度数节点更少。这一实验验证了前面提出的独立集免疫策略使“最大连通分支中存在度数较大的节点”这一结论,同时说明在图 1的实验中,独立集目标免疫使网络仍保留有度数更高的节点,传播速度更快。图 3的实验选择第一大独立集,对于其他独立集有完全类似的结果。
2.2 独立集的随机免疫研究无标度网络对随机免疫策略完全失效,但随机免疫策略与其他免疫策略(目标免疫、熟人免疫)相比较又有方法简便、成本低、无需知道网络的全局信息和可操作性强等优点。
下面的实验是比较初始在独立集中随机免疫一定比例的节点与在全网络中随机免疫相同数目的节点,再随机感染网络中的10个节点,对比这2种免疫方法对传播的影响。网络模型为BA、传播模型是SI,传播方式和模型参数与图 1的实验相同。图 4中IN、AN分别表示的是,IN:初始随机免疫第一大独立集里的一定比例的节点,然后随机感染全网络10个节点,让流行病传播;AN:初始随机免疫全网络中相同数目的节点(与独立集中免疫的节点数目相同),同样随机感染全网络10个节点,让流行病传播。在传播平衡时,I态节点越少说明免疫的效果越好。
|
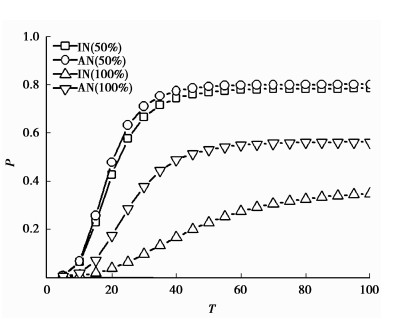
图 4 BA网络模型初始随机免疫第一大独立集中50%、100%的节点。横轴:传播时间;纵轴:传播时I态粒子个数占整个网络节点数目的比例。 |
从图 4的实验可以得到如下结论:无论免疫节点数目的多少,最终独立集的随机免疫均好于全网络的随机免疫;随着免疫节点比例的增加(此时两种免疫方式,免疫的节点数目相同),独立集的优势越来越明显,原因就是独立集中的节点一定不相邻,在网络中更加分散,随着免疫节点地增加,对网络的连通性破坏更大[12],这一免疫方法对传播地阻碍作用也更大。对于其他独立集的实验,与第一大独立集有完全类似的结果。
在对无标度网络的鲁棒性研究中知道,网络对目标攻击是十分脆弱的[20],即去掉网络中的高度数节点会对网络的连通性产生更大地破坏。因此有没有可能是在去掉同样数目的顶点的前提下,随机在全网络中选择的顶点与在独立集中随机选择相同数目的顶点,独立集中选择的高度数顶点更多呢?直觉似乎如此,但从表 1中实验数据可以否定这样的猜测。在表 1的实验中,所用网络模型与图 4的相同。表中第一行表示随机免疫第一大独立集中顶点比例,即在独立集中随机免疫顶点数目,在对全网络进行随机免疫时,免疫相同数目的顶点。第二行代表在独立集中随机免疫的顶点度数之和,第三行表示在全网络中随机免疫的顶点度数和。从表中可以发现这2种免疫方式免疫顶点的度数和十分接近,在两种免疫方法所免节点数目相同时,仅仅从免疫高度数节点的角度,独立集并不占有优势,否则独立集中免疫节点的度数和会高于全网络随机免疫节点的度数和。虽然免疫方法不同,免疫掉的节点在度数上具有相似性。
| 表 1 独立集中随机免疫的顶点与全网络中随机免疫的顶点度数和 |
提出了一种新的免疫策略:对独立集中度数最大节点的免疫。将这一免疫策略与免疫全网络中度数最大节点(2种免疫方式最终免疫掉的节点总度数和相等)相比较,得到独立集的免疫策略更好。这2种免疫方法等价于在网络中去掉相同数目的边,这等同于提出了免疫网络中边的方法。用数值实验说明了免疫独立集中度数最大节点效果更好的原因。对已有的基于独立集的随机免疫策略[12]进行了更进一步地研究,说明这一免疫策略并不是在独立集中免疫掉更多高度数节点,实验阐明基于独立集的随机免疫策略与全网络的随机免疫策略使免疫掉的节点度数的总和十分接近,即这2种免疫方法在免疫节点的度数方面具有相似性。SI传播模型中的节点只有2种状态(S态和I态),这对研究网络结构与免疫的影响提供了相对单纯的环境,可以更好的看到网络结构对于免疫的影响。SIR、SIS和SI是常用的3种传播模型,随着复杂网络免疫研究的发展,对于复杂网络的免疫策略也越来越多,比较不同的免疫策略更适合于何种传播模型将是一个有趣的问题。
| [1] | Tang M, Liu L, Liu Z H. Influence of dynamical condensation on epidemic spreading in scale-free networks[J]. Physical Review E, 2009, 79(1): 16–18. |
| [2] | Erdos P. Graph theory and probability[J]. Canadian Journal of Mathematics, 1959, 11(1): 34. |
| [3] | Watts D J, Strogatz S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(6684): 440–442. DOI:10.1038/30918 |
| [4] | Barabási A L, Albert R. Emergence of scaling in random networks[J]. science, 1999, 286(5439): 509–512. DOI:10.1126/science.286.5439.509 |
| [5] | Anderson R M, May R M, Anderson B. Infectious diseases of humans:dynamics and control[M]. Oxford: Oxford university press, 1992. |
| [6] | Callaway D S, Newman M E J, Strogatz S H, et al. Network robustness and fragility:Percolation on random graphs[J]. Physical Review Letters, 2000, 85(25): 54–68. |
| [7] | Pastor-Satorras R, Vespignani A. Immunization of complex networks[J]. Physical Review E, 2002, 65(3): 41–48. |
| [8] | Cohen R, Havlin S, Ben-Avraham D. Efficient immunization strategies for computer networks and populations[J]. Physical Review Letters, 2003, 91(24): 7901. |
| [9] | Dezsö Z, Barabási A L. Halting viruses in scale-free networks[J]. Physical Review E, 2002, 65(5): 55–103. |
| [10] | Hayashi Y, Minoura M, Matsukubo J. Oscillatory epidemic prevalence in growing scale-free networks[J]. Physical Review E, 2004, 69(1): 21–28. |
| [11] | 张先迪, 李正良. 图论及其应用[M]. 北京: 高等教育出版社, 2005. |
| [12] |
黄斌, 赵翔宇, 齐凯, 等.
复杂网络的顶点着色及其在疾病免疫中的应用[J]. 物理学报, 2013, 62(21): 518–525.
HUANG Bin, ZHAO Xiangyu, QI Kai, et al. Coloring the complex networks and its application for immunization strategy[J]. Acta Physica Sinica, 2013, 62(21): 518–525. (in Chinese) |
| [13] | Dall'Asta L, Pin P, Ramezanpour A. Statistical Mechanics of maximal independent sets[J]. Physical Review E, 2009, 80(6): 121–128. |
| [14] | Klotz W. Graph coloring algorithms[J]. Mathematics Report, 2002: 1–9. |
| [15] | Bollobás B. Modern graph theory[M].[s.l.] Springer, 1998. |
| [16] | Welsh D J A, Powell M B. An upper bound for the chromatic number of a graph and its application to timetabling problems[J]. The Computer Journal, 1967, 10(1): 85–86. DOI:10.1093/comjnl/10.1.85 |
| [17] | Klotz W. Graph coloring algorithms[J]. Mathematics Report, 2002: 1–9. |
| [18] | 汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006. |
| [19] | 马知恩, 传染病动力学的数学建模与研究[M]. 上海:科学出版社[M]. 2004. |
| [20] | Albert R, Jeong H, Barabási A L. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6794): 378–382. DOI:10.1038/35019019 |
 2014, Vol. 37
2014, Vol. 37

