2. 宿州学院 信息工程学院, 安徽 宿州 234000
2. College of Information Engineering, Suzhou University, Suzhou, Anhui 234000, China
无线传感器网络(wireless sensors network,WSN)中的节点定位算法分为基于测距的定位算法与无需测距的定位算法[1-2]。前者算法精度较高,但实施时需要特殊的硬件,成本较高;后者无需额外的硬件,是目前备受关注的定位算法[3-4],广泛应用到大规模无线传感器网络中。
DV-Hop算法[5-6]具有开销小且实现简单等优点,是WSN中一种应用较多的定位算法。但该算法易受网络结构的影响,导致定位误差大、定位准确度低。针对此问题,国内外很多学者对其进行了改进。Hu等[7]对平均每跳距离进行加权处理;Zhang等[8]提出转发一组相邻之间角度重叠的节点以提高定位精度;林金朝等[9]采用多边定位法和泰勒级数展开法求解位置节点的坐标位置;任红建等[10]利用RSSI测距技术对跳数和平均每跳距离进行修正;刘艳文等[11]引进RSSI模型,对DV-HOP的定位过程进行限制;周小波等[12]对节点间的跳数利用RSSI进行加权处理;赵雁航[13]通过改进锚节点广播的数据分组结构、加权处理参考锚节点的平均每跳距离的误差以及对定位中的迭代过程用用改进粒子群算法进行优化的方式来提高DV-HOP算法的定位精度。文中重点分析了DV-Hop算法定位过程中3个阶段带来的误差,在参考文献[12-13]的基础上,利用RSSI值改进DV-Hop算法定位过程中的3个阶段,并用仿真验证改进算法的性能。
1 DV-Hop算法DV-Hop算法基本思想是通过跳数乘以平均跳距估算锚节点和未知节点之间的距离。
1.1 计算节点间的最小跳数锚节点将包含自身坐标位置、编号和跳数的分组向邻居节点广播。邻居节点记录下分组信息,忽略来自相同编号而跳数值较大的分组。将跳数值加1后转发给其邻居节点。这个阶段完成后,全部节点得出与各锚节点的最小跳数。
1.2 估算节点间距离完成阶段(1)后,各锚节点利用式(1)计算平均每跳距离。
| $ {{n}_{i}}=\sum\limits_{j\ne i}{\sqrt{{{\left( {{x}_{i}}-{{x}_{j}} \right)}^{2}}+{{\left( {{y}_{i}}-{{y}_{j}} \right)}^{2}}}/\sum\limits_{j\ne i}{{{m}_{j}}}}, $ | (1) |
其中(xi,yi)和(xj,yj)分别表示锚节点i和j的位置,mj为i与j之间的最小跳数。然后,锚节点将计算出的m广播至网络中,未知节点收到后,用n×m即可得到2者之间的估算距离。
1.3 计算未知节点的坐标位置利用3个或3个以上锚节点的估算距离,使用三边测量法或极大似然估计法测算其坐标位置。
2 RMDV-Hop算法WSN中,节点随机分布。为了提高DV-HOP算法的定位精度,RMDV-Hop算法从定位过程的3个阶段进行了改进。
2.1 跳数修正节点之间以一定的概率连通。距离很近时,2个节点连通概率较高。节点之间的跳数均为1时无法区分远、近2种情况。针对此问题,RMDV-Hop算法将借助RSSI值来计算跳数值,这样可以大大降低定位误差。
RSSI利用信号传递过程中强度衰减特性来进行估算节点间的距离,距离为d的接收节点接收的信号强度Pr(d)可通过路径损耗阴影模型得到
| $ {{P}_\text{r}}\left( d \right)=\frac{{{P}_\text{r}}\left( {{d}_{0}} \right)}{{{\left( d/{{d}_{0}} \right)}^{\gamma }}}+z, $ | (2) |
式中:d为发送端与接收端的距离,d0为设置的发射端的参考距离,γ是信号衰减因子,z服从均值为0,方差为σ2的高斯分布。从路径损耗阴影模型可以看出,在其他条件均相同情况下,节点间距离越近,无线信号耗散越小,在接收端测得RSSI值越大,反之,在接收端测得RSSI值越小,因此可用节点间RSSI值来比征节点间的距离大小。RSSI值可通过节点自身的无线通信模块提供,无需增加硬件。
DV-Hop算法的原则是:节点只接受网络中最小的跳数值。实验表明:多数节点的误差在接收到m=1的情形时比较大[8]。因此RMDV-Hop算法对节点m=1的情形采用文献[9]方法进行修改。对于跳数大于1的,不作任何处理。具体过程如下:
1) 锚节点向其直接邻居节点广播分组{xi,yi,si,m,RSSIi},其中xi,yi为锚节点的坐标,si是该节点的编号,m是跳数值,初始化为0,RSSIi是节点接收分组时的信号强度,初始化为0;
2) 收到分组后,直接邻居节点记下分组信息,将RSSIi记为接收该元组时的RSSI值,将m加1,然后将该分组转发给其邻居节点;邻居节点根据接收元组时的RSSI值R计算权值wi=RSSIi/R,利用权值加权处理元组中的m值:m=m+w,继续转发该分组。
3) 如果节点接收到相同编号的元组,则与自己表中的m值比较,忽略大于当前值的m;小于则返回步骤2)对跳数进行加权处理。
由于WSN中节点随机分布且数量庞大,因而广播过程中数据分组会出现冲突或碰撞。一旦发生,会丢失该分组的信息,导致节点间的最小跳数发生偏差,影响正常定位过程,重发数据分组,会加重网络负担。因此本算法设定在允许范围内的最大传播跳数来降低分组在传播中发生冲突或碰撞的概率。
2.2 修正平均每跳距离DV-Hop算法中,未知节点只用距离它跳数最小的锚节点平均跳距,而一个参考节点不能完全准确反映整个网络的属性,因而导致产生较大的定位误差。为了降低未知节点的定位误差,RMDV-Hop算法将与其距离最近的N个锚节点作参考节点。
全部锚节点分组收到后,未知节点对锚节点依其RSSI值从大到小排序,采用RSSI值大的前N个锚节点计算未知节点的平均每跳距离。锚节点利用式(1)计算平均每跳距离,计算锚节点i与j之间的估算距离为
| $ {{d}_{\text{e}ij}}={{m}_{ij}}\times {{n}_{ij}}, $ | (3) |
根据记录的节点位置信息,计算出锚节点i与j之间的实际距离为
| $ {{d}_{\text{t}ij}}=\sqrt{{{\left( {{x}_{i}}-{{x}_{j}} \right)}^{2}}+{{\left( {{y}_{i}}-{{y}_{j}} \right)}^{2}}}, $ | (4) |
锚节由此可达到锚节点i的平均每跳距离误差为
| $ {{\varepsilon }_{i}}=\frac{\sum\limits_{i\ne j}{\left| {{d}_{\text{t}ij}}-{{d}_{\text{e}ij}} \right|/{{m}_{ij}}}}{N-1}。$ | (5) |
ε越小的锚节点,对未知节点的平均每跳距离值估计影响越大,因此,将较大的权值赋给ε较小的锚节点,从而提高未知节点的定位精度。每个锚节点权值为
| $ {{\omega }_{i}}=\frac{\frac{1}{{{\varepsilon }_{i}}}}{\sum\limits_{k=1}^{N}{\frac{1}{{{\varepsilon }_{k}}}}}, $ | (6) |
未知节点的平均每跳距离为
| $ {{d}_{\text{hop}}}\text{=}\sum\limits_{i=1}^{N}{{{\omega }_{i}}\times {{n}_{i}}}, $ | (7) |
按照平均每跳距离的误差不同给作为参考节点的N个锚节点赋予不同的权值,能够更加全面准确地反映网络的真实情况,提高了未知节点的平均每跳距离的准确度,解决了WSN无需测距定位算法定位误差较大的问题。
2.3 采用总体最小二乘法计算未知节点坐标总体最小二乘法充分考虑了由GPS自身定位产生的位置偏差引起的锚节点位置误差及节点间距离误差,能够体现未知节点坐标计算受这两种误差的影响,提高未知节点的坐标的精确性。
当未知节点i得出3个及以上dpi后,与DV-Hop算法不同,采用文献[14-15]描述的总体最小二乘法计算未知节点的坐标。
2.4 算法流程针对DV-Hop算法定位误差较大的问题,文中提出RMDV-Hop算法,其流程如图 1所示。
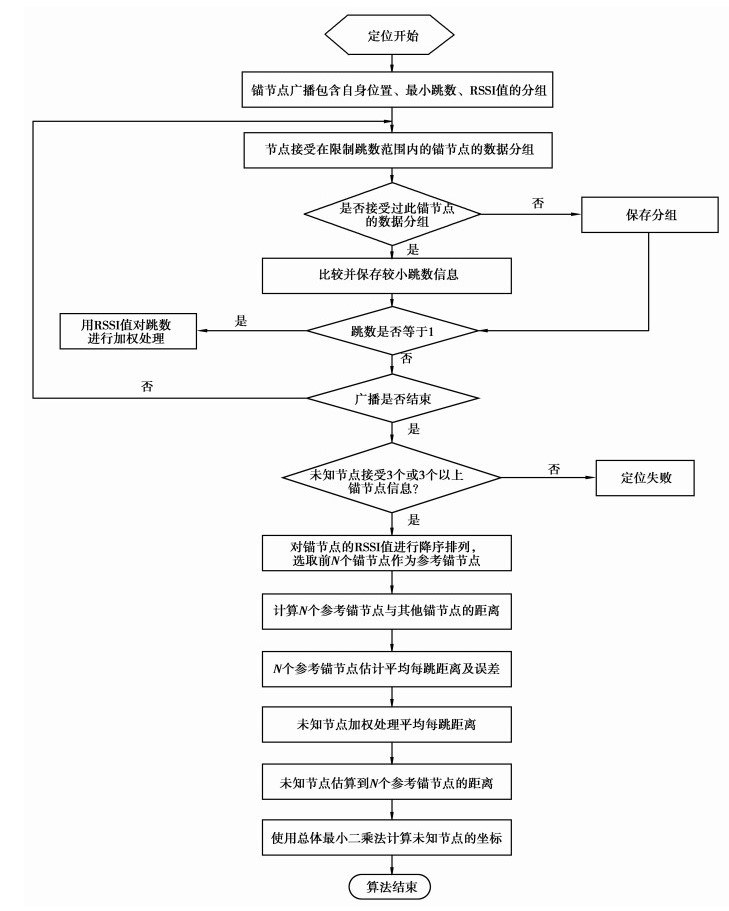
|
图 1 RMDV-Hop算法流程图 |
研究采用MATLAB 7.0对算法进行仿真。仿真环境中,锚节点和未知节点随机分布,区域为:[0, 150]×[0, 150],初始节点分布如图 2所示。
|
图 2 节点分布图 |
算法精度是衡量算法最重要的指标。将DV-Hop定位算法、RMDV-Hop算法在定位误差上进行比较来验证文中算法的性能。计算定位误差为
| $ {\delta _i} = 100\% \times \sqrt {{{\left( {{x_{\rm{t}}} - {x_{\rm{e}}}} \right)}^2} + {{\left( {{y_{\rm{t}}} - {y_{\rm{e}}}} \right)}^2}} /R, $ | (8) |
式中(xt,yt),(xe,ye)分别是节点的真实位置和估计位置,R是节点的通信半径。对每个实验场景都执行多次并对结果取平均,使得到的实验数据更客观。
3.2 结果分析网络中取总的节点数目为100个,改变通信半径,分别采用DV-Hop算法和RMDV-Hop算法在不同锚节点数量下仿真,多次执行定位算法程序计算出未知节点的坐标,再利用式(7)求出每次定位的误差;对同条件下的多个误差取平均值,仿真性能比较如图 3所示。
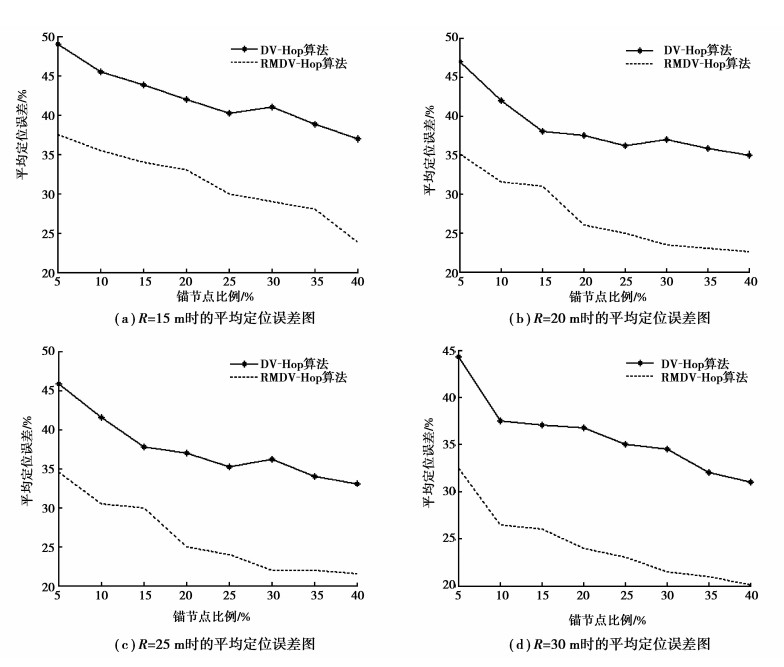
|
图 3 平均定位误差图 |
图 3表明,随着锚节点所占比例的增大,平均定位误差均不断降低。在通信半径相同,锚节点比例也相同的条件下,传统DV-Hop算法定位误差较大,RMDV-Hop算法误差较小。其他条件相同,通信半径变大,能够降低定位误差。RMDV-Hop算法定位精度比比传统DV-Hop算法平均提高了18%~28%。
图 4表明了在不同的通信半径下,RMDV-Hop算法平均定位误差均随着锚节点比例增大而降低。随通信半径的增大,定位误差逐渐减小,定位误差在R取30时最小。
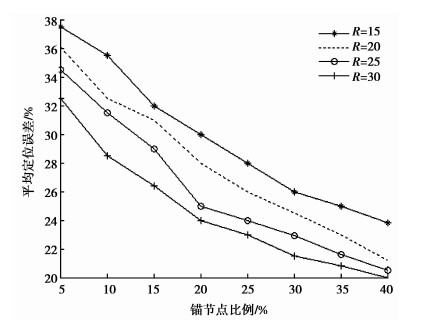
|
图 4 RMDV-Hop算法在不同通信半径下的定位误差对比 |
将50个节点随机分布,信标节点数保持不变,增加未知节点个数,通信半径取R=50 m,其他条件不作变化,比较文中算法和DV-HOP算法的平均定位误差。
图 5显示了比较的结果,2种定位算法的定位误差均随着节点数的增加而降低,在节点数为300时趋向平稳,定位精度在信标节点数目不变的条件下,文中改进算法的定位精度比传统DV-Hop算法平均提高了14% ~20%。
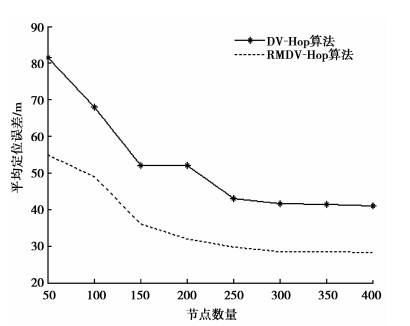
|
图 5 不同节点数的平均定位差比较 |
仿真结果表明,RMDV-Hop算法的定位误差明显低于传统的DV-Hop算法。由于网络中的所有节点均随机分布,网络的结构受锚节点数目、总节点数目的改变影响,导致定位误差不是直线下降而是曲线变化,仿真结果证明了这点。但是文中所提的RMDV-Hop算法没有太剧烈的振动,定位误差呈平稳下降,算法稳定性和性能较好。
4 结论DV-Hop算法在节点随机分布的网络环境中,定位不准、误差较大。为了减少定位误差,文中提出了RMDV-Hop算法。改进算法利用RSSI值对跳数是1的跳数值作了加权处理并限制了网络中广播的最大跳数值,并根据RSSI值选出对未知节点定位有较大影响的N个锚节点作为参考节点,加权处理参考锚节点平均每跳距离的误差;最后根据总体最小二乘法得出未知节点的坐标。仿真结果验证,RMDV-Hop算法在没有增加新的硬件条件下,WSN明显提高了算法的定位精度和稳定性。
| [1] | 孙利民, 李建中, 陈渝, 等. 无线传感器网络[M]. 北京: 清华人学出版社, 2005: 148-149. |
| [2] | He T, Huang C, Blum B M, et al. Range-free localization schemes in large scale sensornetworks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking. New York:ACM Press, 2003:81-95. |
| [3] |
王福豹, 史龙, 任丰原.
无限传感器网络中的自身定位系统和算法[J]. 软件学报, 2003, 16(5): 857–868.
WANG Fubao, SHI Long, REN Fengyuan. Self-Localization systems and algorithms for wireless sensor networks[J]. Journal of Software, 2003, 16(5): 857–868. (in Chinese) |
| [4] | Hsieh Y L, Wang K. Efficient localization in mobile wireless sensor networks[C]//Sensor Networks, Ubiquitous, and Trustworthy Computing, 2006. IEEE International Conference on. IEEE, 2006, 1:5 pp. |
| [5] | Niculescu D, Nath B. DV based positioning in ad hoc networks[C]. Journal of Telecommunication Systems, 2003, 22(1/4):267-280. |
| [6] | Niculescu D, Nath B. Ad hoc positioning system (APS)[C]//IEEE Global Telecommunications Conference (GLOBECOM'01).San Antonio, Texas, USA, 2001.2926-2931. |
| [7] | Hu Y, Li X. Based on DV-HOP algorithm for wireless sensor network node positioning technology[M]. Shanxi: Taiyuan University of Technology, 2012: 5. |
| [8] | Zhang X, Xie H. Wireless sensor networks in an improved DV-Hop localization algorithm Hunan:Wuhan University of Technology, 2008, 3. |
| [9] |
林金朝, 李小玲, 刘海波.
无线传感器网络DV-Hop算法改进与性能[J]. 重庆大学学报, 2010, 33(2): 127–132.
LIN Jinzhao, LI Xiaoling, LIU Haibo. Improvement and performances of DV-hop local ization algorithm in wireless sensor networks[J]. Journal of Chongqing University, 2010, 33(2): 127–132. DOI:10.11835/j.issn.1000-582X.2010.02.023 (in Chinese) |
| [10] |
任红建, 朱玲玲, 杨爱琴.
基于RSSI测距和DV-HOP误差修正的WSN节点定位[J]. 计算机测量与控制, 2012, 20(10): 2863–2866.
REN Hongjian, ZHU Lingling, YANG Aiqin. Localization algorism for sensor node based on RSSI ranging and DV-Hop error correcting[J]. Computer Measurement & Control, 2012, 20(10): 2863–2866. (in Chinese) |
| [11] |
刘艳文, 王福豹, 段渭军, 等.
基于DV-Hop定位算法和RSSI测距技术的定位系统[J]. 计算机应用, 2007, 27(3): 516–518.
LIU Yanwen, WANG Fubao, DUAN Weijun. A localization system based on DV-Hop localization algorithm and RSSI ranging technique[J]. Journal of Computer Applications, 2007, 27(3): 516–518. (in Chinese) |
| [12] |
周小波, 乔钢柱, 曾建潮.
无线传感器网络中基于RSSI的加权DV-HOP定位方法[J]. 计算机工程与应用, 2011, 47(14): 109–111.
ZHOU Xiaobo, QIAO Gangzhu, ZENG Jianchao. RSSI based weighted DV-HOP localization algorithm for Wireless Sensor Networks[J]. Computer Engineering and Applications, 2011, 47(14): 109–111. DOI:10.3778/j.issn.1002-8331.2011.14.030 (in Chinese) |
| [13] |
赵雁航, 钱志鸿, 尚小航, 等.
基于跳距修正粒子群优化的WSN定位算法[J]. 通信学报, 2013, 34(9): 105–114.
ZHAO Yanhang, QIAN Zhihong, SHANG Xiaohang, et al. PSO localization algorithm for WSN nodes based on modifying average hop distances[J]. Journal on Communications, 2013, 34(9): 105–114. (in Chinese) |
| [14] | 魏木生. 广义最小二乘为题的理论和计算[M]. 北京: 科学出版社, 2006: 107-114. |
| [15] | 于宁. 无限传感器网络定位优化方法[D]. 北京: 北京邮电大学, 2008: 15-17. http://d.wanfangdata.com.cn/Thesis/Y1317858 |
 2014, Vol. 37
2014, Vol. 37

