橡胶衬套是电动车悬架系统高频减振的重要元件,中高频范围内橡胶衬套的有限元建模是电动车用橡胶衬套的重要研究点[1]。
基于实验的橡胶衬套动态特性研究已较成熟。Slawomir[2]基于实验,提出半经验模型,能够表现出频率和振幅对模型动刚度和阻尼系数的影响,与实际情况比较相符,但模型在高频率、小振幅工况下,阻尼系数的变化规律与实验结果相差较大。而且橡胶衬套动态特性不仅受材料特性影响,其结构也是一个重要因素。同样橡胶材料应用于不同衬套结构,需重新做模型参数的识别甚至是模型的修改,非常不方便。基于实验研究的橡胶衬套半经验公式没有通用性,不适用于工程应用。因此, 有必要研究橡胶的材料特性,求出其本构方程,并将其转换为有限元软件中的材料参数,将结构的因素交给网格划分去处理,而材料特性的部分交给材料本构模型去处理。
为了描述橡胶材料的振幅相关性,前人提出了很多不同的摩擦模型,都有各自的优缺点[3-9]。但是少有研究提出可行的办法将材料的力学行为特性模型转化为有限元环境中的材料本构模型,无法将这些力学特性模型应用到有限元分析中。笔者将基于橡胶材料实验,揭示橡胶材料的本构关系。采用带屈服过程的塑性单元来描述橡胶材料的振幅相关性,对塑性单元的动刚度和阻尼角进行理论计算,确定选用塑性单元的个数和屈服点的分布。提出一种弹性单元、粘弹单元和塑性单元集成的橡胶材料粘弹塑性本构模型,并根据实验数据来拟合该集成本构模型中的材料参数。再将该理论模型转化为ABAQUS中的材料参数,通过ABAQUS中一个简单剪切实验仿真,分析理论模型和有限元模型的差别,在此基础上找出优化有限元模型中材料参数的方法。
1 橡胶材料动态特性参数的实验获取橡胶衬套中橡胶材料动态特性参数的获取,需要基于材料的纯剪切实验。这就需要从橡胶衬套中取出一个长方体的橡胶块出来,但由于橡胶衬套体积很小,内部填充的胶料有限,一般不太可行。
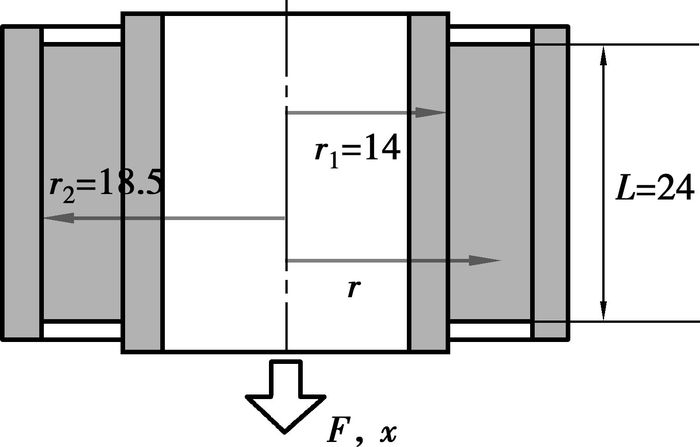
图 1为典型的车用橡胶衬套,由内圈、外圈以及其中的橡胶组成。具体的内部几何参数如图 2所示。

|
图 1 实验用橡胶衬套 |
|
图 2 实验用橡胶衬套几何参数 |
这种橡胶衬套结构非常简单,内圈没有阶梯轴结构,橡胶也没有挖孔。在橡胶衬套发生轴向运动时,可以认为橡胶是发生纯剪切。因此, 可以根据橡胶衬套的轴向位移加载实验来代替橡胶材料的纯剪切实验。当内外圈半径比值很小时,橡胶材料可以看作只发生纯剪切。
橡胶材料动态剪切模量Gdyn为:
| $ {G_{{\rm{dyn}}}} = {K_{{\rm{dyn}}}} \cdot \frac{{\ln \left( {{r_2}/{r_1}} \right)}}{{2{\rm{ \mathsf{ π} }}L}}。$ | (1) |
对于橡胶衬套而言,阻尼角表示的是力与位移的相位差;对于材料剪切实验而言,阻尼角表示应力与应变的相位差。这两者是一致的,可以直接用橡胶衬套轴向实验得到的阻尼角来表示材料剪切实验中应力与应变的相位差。
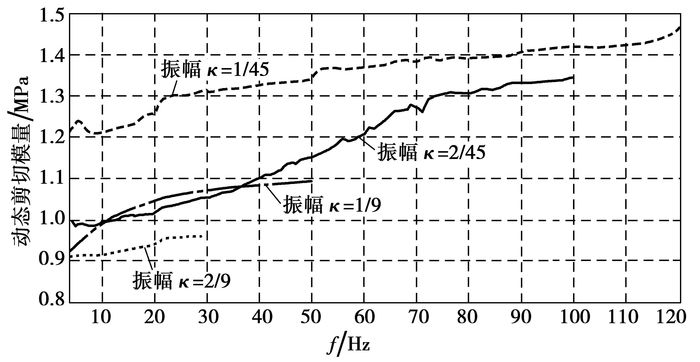
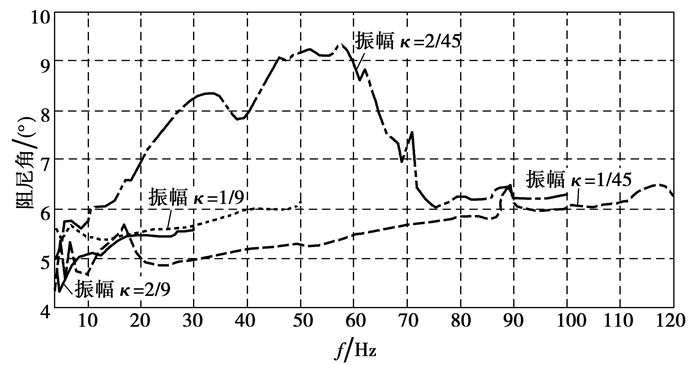
根据上面的分析,将橡胶衬套轴向实验数据转化为纯剪切实验的动态剪切模量和阻尼角,结果如图 3和图 4所示。总体来说,动态剪切模量在各个振幅下都随频率的增大而增大,并随振幅的增大而减小;阻尼角在振幅为2/45时随频率的增大先增大后减小,在其他振幅工况下随频率的增大而增大;阻尼角先随着振幅的增大而增大,在振幅为2/45时达到极值,然后随着振幅的增大又逐渐减小。
|
图 3 不同振幅下动态剪切模量随频率变化的实验数据 |
|
图 4 不同振幅下阻尼角随频率变化的实验数据 |
采用多个Maxwell单元并联模型这种橡胶材料粘弹模型来模拟其频率相关性。采用加入屈服强化过程的塑性模型来描述橡胶材料的振幅相关性。基于能量损耗原理将弹性单元、粘弹单元和塑性单元这三个理论模型集成为橡胶材料的粘弹塑性本构模型。
2.1 橡胶材料粘弹模型多个Maxwell单元并联模型这种橡胶材料粘弹模型的应力应变的线性微分本构方程可以表示为:
| $ \begin{array}{*{20}{c}} {\tau = G \cdot \kappa + \sum\limits_{i = 1}^N {{G_i}\left( {\kappa - {\kappa _i}} \right)} ,}\\ {{G_i}\left( {\kappa - {\kappa _i}} \right) = {\eta _i} \cdot {{\dot \kappa }_i}。} \end{array} $ | (2) |
可得到频域的剪切存储模量:
| $ {G_{\rm{s}}}\left( \omega \right) = G + \sum\limits_{p = 1}^N {{G_p}\frac{{{\omega ^2}x_p^2}}{{1 + {\omega ^2}x_p^2}}} 。$ | (3) |
剪切损失模量:
| $ {G_{\rm{l}}}\left( \omega \right) = \sum\limits_{p = 1}^N {\frac{{{\eta _p}\omega }}{{1 + {\omega ^2}x_p^2}}} 。$ | (4) |
进而得出多个Maxwell并联模型的动态剪切模量和阻尼角表达式分别为:
| $ {{G_{{\rm{dyn}}}}\left( \omega \right) = \sqrt {G_{\rm{s}}^2 + G_{\rm{l}}^2} ,} $ | (5) |
| $ {\theta = {{\tan }^{ - 1}}\left[ {{G_{\rm{l}}}\left( \omega \right)/{G_{\rm{s}}}\left( \omega \right)} \right]。} $ | (6) |
笔者采用加入屈服强化过程的塑性模型来描述橡胶材料的振幅相关性。
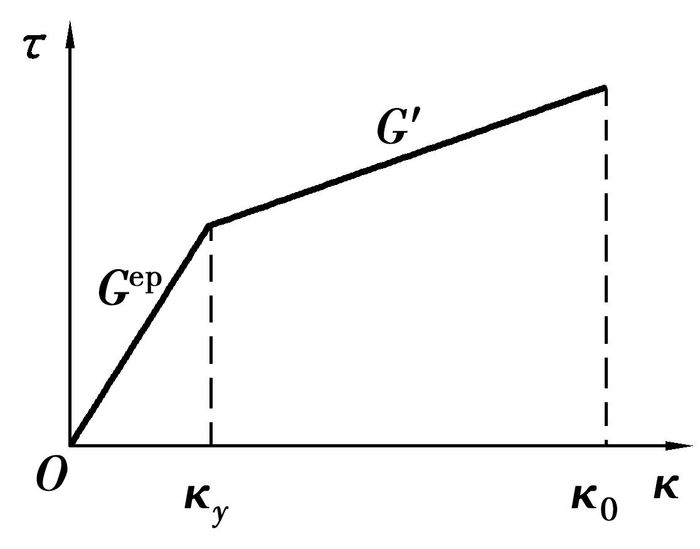
2.2.1 塑性单元动刚度和阻尼角的理论计算图 5所示为带强化过程的塑性模型。它与简单塑性模型最大的不同在于单元发生屈服之后,剪切模量不会直接变为零,而是相对于屈服前的剪切模型有所减小。
|
图 5 带强化过程的弹塑性模型 |
根据塑性单元的材料定义,可推断出其迟滞回线,从而根据迟滞回线计算塑性单元的动态剪切模量和阻尼角。
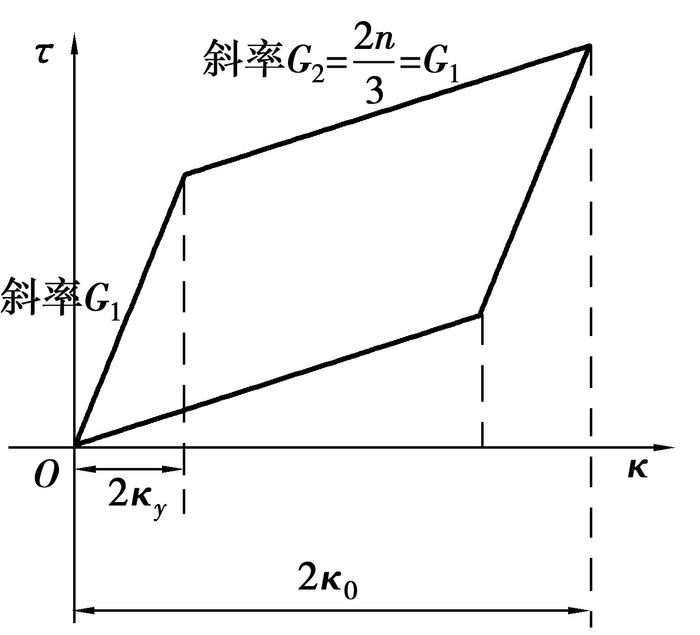
指定材料定义的塑性模型迟滞回线如图 6所示。迟滞回线包围面积,即一个循环内模型能量损耗:
|
图 6 指定材料定义的塑性模型迟滞回线 |
| $ {S_{四边形}} = 4{\kappa _y}\left( {{\kappa _0} - {\kappa _y}} \right)\left( {{G_1} - {G_2}} \right)。$ | (7) |
单个塑性单元的动刚度:
| $ {G^{{\rm{ep}}}} = \left( {{G_1}{\kappa _y} + {G_y}\left( {{\kappa _0} - {\kappa _2}} \right)} \right)/{\kappa _0}。$ | (8) |
单个塑性单元的阻尼系数:
| $ \sin \theta = {S_{四边形}}/\left[ {{\kappa _0} \cdot \left( {{G_1}{\kappa _y} + {G_2}\left( {{\kappa _0} - {\kappa _y}} \right)} \right) \cdot {\rm{ \mathsf{ π} }}} \right]。$ | (9) |
如果有两个或多个塑性单元叠加,则叠加塑性模型的动态剪切模量是两个或多个的叠加,阻尼角可以根据能量损耗原理计算,不在此详述。
2.2.2 塑性单元个数的选择若采用多个塑性单元的叠加,例如3个,屈服应变由小到大依次是:κy1, κy2, κy3。它们可能有如表 1所示的几种屈服点分布形式。
| 表 1 3个塑性单元的4种屈服点分布形式 |
第1种屈服点分布形式的屈服方程为:
| $ \left. \begin{array}{l} G_1^{{\rm{ep}}} + G_2^{{\rm{ep}}} + G_3^{{\rm{ep}}} + {G_{\rm{a}}} = {G_0},\\ \frac{{\left[ {G_1^{{\rm{ep}}}{\kappa _{{y_1}}} + \frac{{2n}}{3}G_1^{{\rm{ep}}}\left( {{\kappa _{01}} - {\kappa _{{y_1}}}} \right)} \right]}}{{{\kappa _{01}}}} + G_2^{{\rm{ep}}} + G_3^{{\rm{ep}}} + {G_{\rm{a}}} = {G_1},\\ \frac{{\left[ {G_1^{{\rm{ep}}}{\kappa _{{y_1}}} + \frac{{2n}}{3}G_1^{{\rm{ep}}}\left( {{\kappa _{02}} - {\kappa _{{y_1}}}} \right)} \right]}}{{{\kappa _{02}}}} + \frac{{\left[ {G_2^{{\rm{ep}}}{\kappa _{{y_2}}} + \frac{{2n}}{3}G_2^{{\rm{ep}}}\left( {{\kappa _{02}} - {\kappa _{{y_2}}}} \right)} \right]}}{{{\kappa _{02}}}} + \\ G_3^{{\rm{ep}}} + {G_{\rm{a}}} = {G_2},\\ \frac{{\left[ {G_1^{{\rm{ep}}}{\kappa _{{y_1}}} + \frac{{2n}}{3}G_1^{{\rm{ep}}}\left( {{\kappa _{03}} - {\kappa _{{y_1}}}} \right)} \right]}}{{{\kappa _{03}}}} + \frac{{\left[ {G_2^{{\rm{ep}}}{\kappa _{{y_2}}} + \frac{{2n}}{3}G_2^{{\rm{ep}}}\left( {{\kappa _{03}} - {\kappa _{{y_2}}}} \right)} \right]}}{{{\kappa _{03}}}} + \\ \frac{{\left[ {G_3^{{\rm{ep}}}{\kappa _{{y_3}}} + \frac{{2n}}{3}G_3^{{\rm{ep}}}\left( {{\kappa _{{0_3}}} - {\kappa _{{y_3}}}} \right)} \right]}}{{{\kappa _{03}}}} + {G_{\rm{a}}} = {G_3}。\end{array} \right\} $ | (10) |
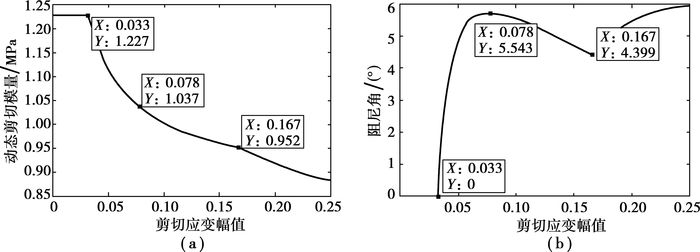
求得塑性叠加模型动态剪切模量和阻尼角如图 7所示。
|
图 7 第1种屈服点分布形式的动态特性计算结果 |
第1种屈服点分布形式的阻尼角计算结果不符合阻尼角随振幅增大先增大再减小的趋势。
第2种屈服点分布形式,也能得到塑性单元材料参数计算方程组。但整理得矩阵A奇异,方程无解,排除这种分布形式。
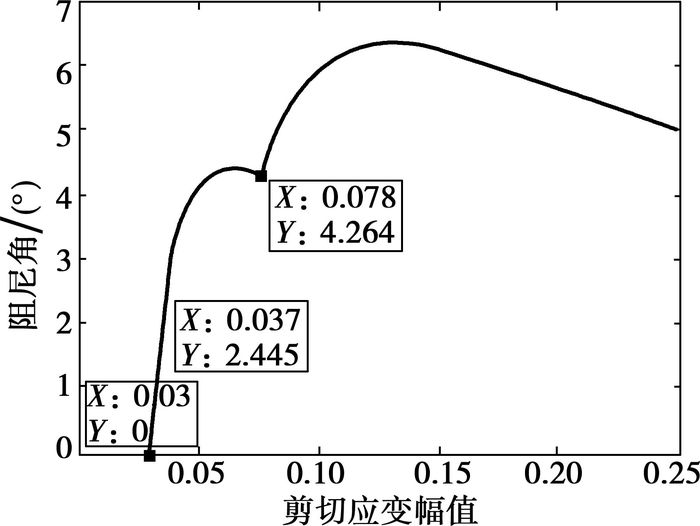
第3种屈服点分布形式的阻尼角计算结果如图 8所示,不符合阻尼角随振幅增大先增大再减小的趋势。
|
图 8 第3种屈服点分布形式的阻尼角计算结果 |
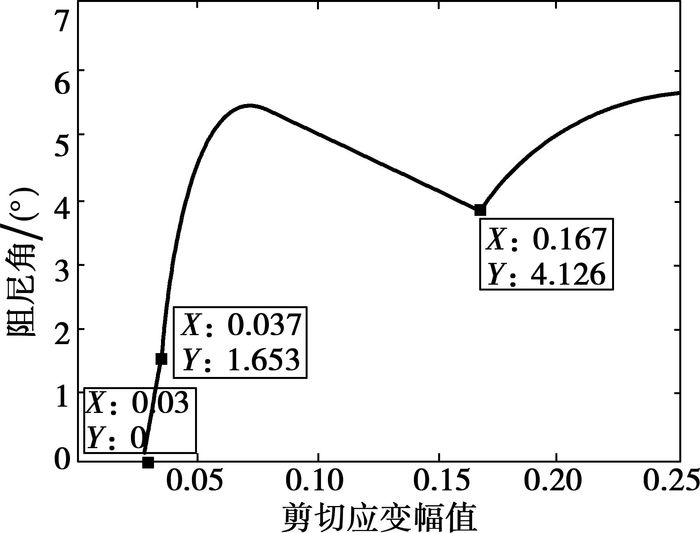
第4种屈服点分布形式的阻尼角计算结果如图 9所示,也不符合随振幅增大先增大再减小的趋势。
|
图 9 第4种屈服点分布形式的阻尼角计算结果 |
根据3个塑性单元动态特性分析可知,动态剪切模量随振幅增大而下降,在屈服点处,下降的斜率变大;阻尼角在没有新的塑性单元发生屈服时,随着振幅增大先增大后减小,遇到新的单元发生屈服时阻尼角突然增大。多个塑性单元叠加,阻尼角随着振幅的变化不满足要求,最好还是采用单个塑性单元。
2.2.3 塑性单元屈服点分布的确定假设κ0=1/45振幅下,塑性单元都没有发生塑性形变。根据实验,橡胶材料的阻尼角随着振幅的增大先增大后减小。可以从理论上找出这个转折点。
由单个塑性单元阻尼角计算公式可以得到:
| $ {\kappa _0} = 2.199{\kappa _y}。$ | (11) |
根据实验数据,振幅达到2/45后阻尼角开始随振幅增大而下降,可以把峰值点取在2/45附近。计算得到κy=0.020 2时峰值点在κ0=2/45处。但是κy>1/45,所以在这个范围内,取值越小越好, 取κy=0.023。
用振幅κ00=1/45和κ02=1/9的实验数据来拟合单个塑性单元的参数, 可得Gep=0.640 43,Ga=0.586 07。
用振幅κ00=1/45和κ02=2/9的实验数据来拟合单个塑性单元的参数,可得Gep=0.780 4,Ga=0.446 1。
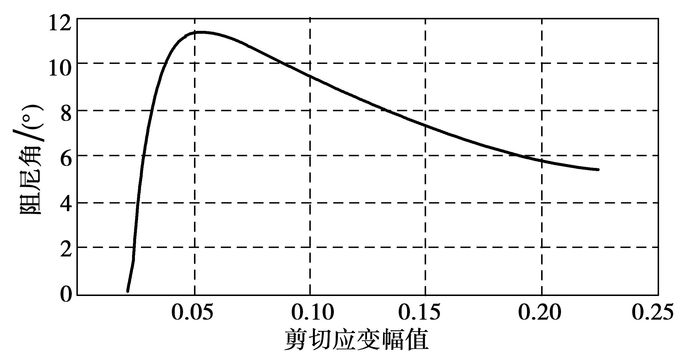
最后根据各个振幅下误差平均且最小的原则,确定了这个塑性单元的材料参数,计算其阻尼角结果如图 10所示。可以看出阻尼角先随着振幅的增加显著增大,在κ0=0.05处达到极大值后,随着振幅的增加又逐渐减小,与实验结果比较符合。
|
图 10 单个塑性单元的阻尼角计算结果 |
基于能量损耗原理将弹性单元、粘弹单元和塑性单元这3个理论模型集成为橡胶材料粘弹塑性模型。
集成模型的动态剪切模量等于粘弹单元动态剪切模量Gdynve与弹塑性单元动态剪切模量Gdynve相加:
| $ {G_{{\rm{dyn}}}} = G_{{\rm{dyn}}}^{{\rm{ve}}} + G_{{\rm{dyn}}}^{{\rm{ep}}}。$ | (12) |
单个周期内,集成模型损失的能量等于粘弹单元损失能量加上塑性单元损失能量:
| $ U = {U^{{\rm{ve}}}} + {U^{{\rm{ep}}}}, $ | (13) |
| $ \frac{U}{{{\rm{ \mathsf{ π} }} \cdot \kappa _0^2}} = \frac{{U \cdot \left( {{\tau _0}/{\kappa _0}} \right)}}{{{\rm{ \mathsf{ π} }}{\tau _0}{\kappa _0}}} = {G_{{\rm{dyn}}}} \cdot {\theta _{{\rm{dyn}}}}。$ | (14) |
则有集成模型的阻尼角:
| $ {\theta _{{\rm{dyn}}}} = \arcsin \left( {\frac{{G_{{\rm{dyn}}}^{{\rm{ve}}}\sin \left( {\theta _{{\rm{dyn}}}^{{\rm{ve}}}} \right) + G_{{\rm{dyn}}}^{{\rm{ep}}}\sin \left( {\theta _{{\rm{dyn}}}^{{\rm{ep}}}} \right)}}{{{G_{{\rm{dyn}}}}}}} \right)。$ | (15) |
根据橡胶材料集成模型的动态剪切模量和阻尼角的理论计算公式即可对模型的材料参数进行拟合。橡胶材料实验共有4个振幅工况,其中最小的振幅为κ0=1/45,在这个振幅下是否有塑性单元发生屈服,有两种不同的参数拟合方法。
假设1:κ0=1/45振幅工况下,模型中的塑性单元(个数还未确定)都没有发生塑性变形。
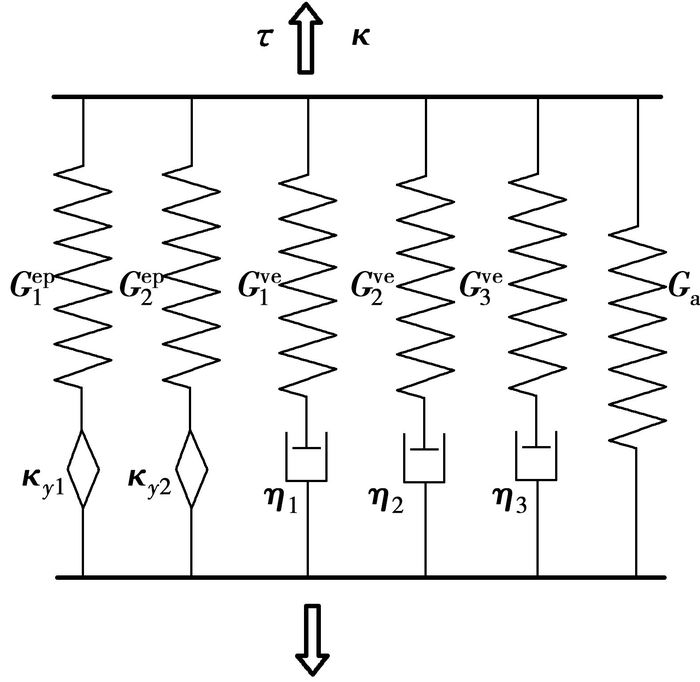
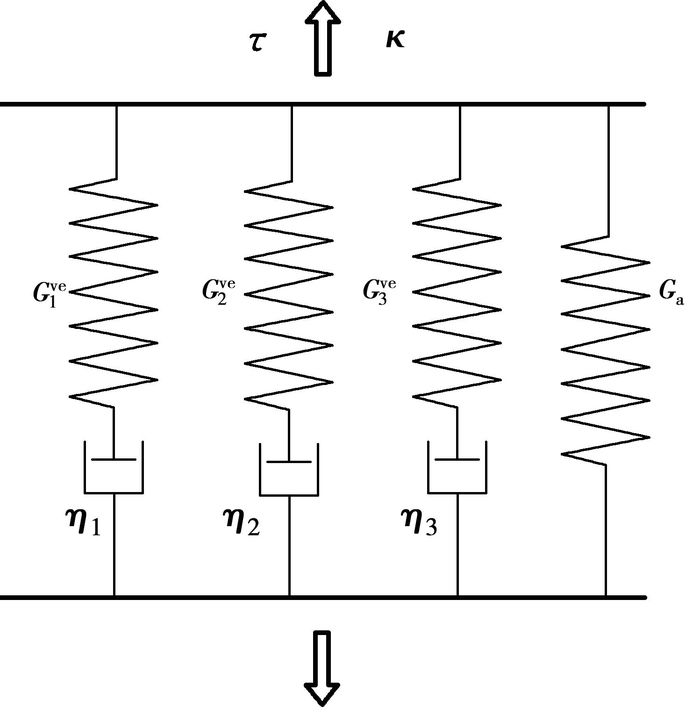
由于κ0=1/45振幅工况下,塑性单元都没有发生屈服,可将图 11所示的粘弹塑性集成模型直接转换成图 12所示的粘弹模型,并通过该工况下实验数据,确定粘性单元的各参数。
|
图 11 粘弹塑性集成理论模型 |
|
图 12 粘弹理论模型 |
对于实验得到的动态剪切模量和阻尼角随频率变化的数据,需调整如图 12所示模型中的各个参数来对其进行模拟,并采用Isight强大的多目标优化方法对橡胶材料参数进行拟合。
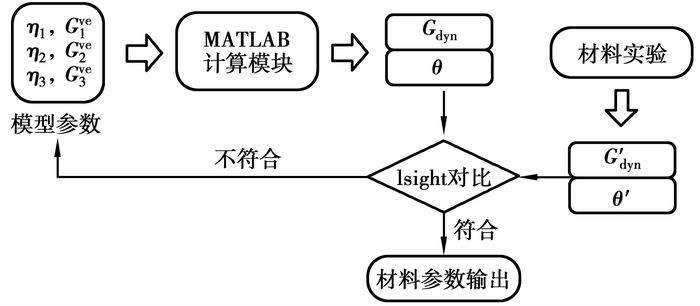
图 13为材料参数拟合流程图。优化目标有两个,分别使模型计算出来的动态剪切模量和阻尼角与实验值的差值最小。采用NSGA-Ⅱ多目标优化方法,优化后得到粘性材料参数。
|
图 13 粘弹理论模型参数拟合流程图 |
为考虑模型的振幅相关性,需把图 13中的线弹簧变成一个线弹簧加一个塑性单元。据前文分析,应选择单个塑性单元,通过Isight优化后得到参数为:κy=0.023,n=0.8,Gep=0.780 4,Ga=0.446 1。
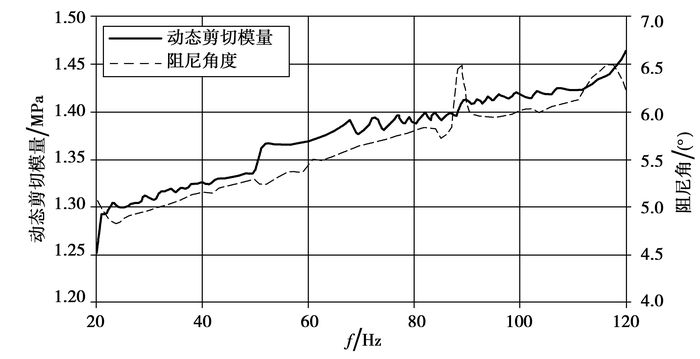
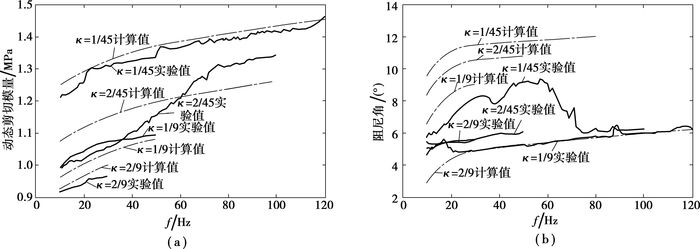
根据求得的材料参数,计算模型的动态剪切模量和阻尼角,κ0=1/45振幅下的计算结果如图 14所示,各振幅工况下的计算结果与实验数据进行对比,如图 15所示。
|
图 14 κ0=1/45振幅下,动态剪切模量和阻尼角的频率相关性 |
|
图 15 第1种假设下叠加模型理论计算与实验对比 |
第1种假设下,各振幅工况,动态剪切模量的计算值与实验值误差较小,拟合较准确;但是阻尼角仅在振幅为1/45时误差较小,其他振幅工况下的误差均过大。
假设2:κ0=1/45振幅工况下,已有塑性单元屈服。
与假设1相反,需先拟合塑性单元参数,再通过Isight优化粘性单元参数。
同样采用单个塑性单元,有κy<1/45,根据之前阻尼角随振幅变化峰值的推论,取κy=0.02,n=0.8。在不考虑粘弹参数影响(激励频率很低,如4 Hz)时,求得
| $ {G^{{\rm{ep}}}} = 0.4024,{G_{\rm{a}}} = 0.8429; $ |
| $ {G^{{\rm{ep}}}} = 0.7054,{G_{\rm{a}}} = 0.5540; $ |
| $ {G^{{\rm{ep}}}} = 0.8638,{G_{\rm{a}}} = 0.4030。$ |
综合考虑4个振幅下的情况,取Gep=0.8,Ga=0.46对应的各个振幅,在低频(4 Hz)工况下的误差:
| $\Delta {g_1} = - 0.31\% ,\Delta {g_2} = - 7.64\% ,\Delta {g_3} = - 3.6\% ,\Delta {g_4} = - 2.25\% 。$ |
根据上面确定的塑性单元模型,选择粘弹材料参数(共6个)作为设计变量,4个不同振幅工况的动刚度和阻尼角实验数据作为设计目标(共8个)。采用叠加模型,基于Isight做粘弹材料的参数优化。求得:
| $ {\eta _1} = 2.1948{\rm{e}} - 4,{G_1} = 0.03680; $ |
| $ {\eta _2} = 6.6999{\rm{e}} - 4,{G_2} = 0.11116; $ |
| $ {\eta _3} = 2.1822{\rm{e}} - 4,{G_3} = 0.30276。$ |
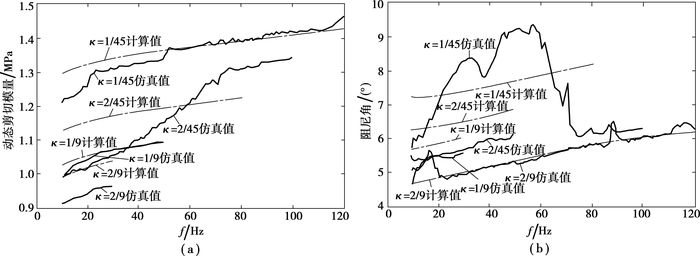
计算模型的动态剪切模量和阻尼角,与实验数据对比,结果如图 16所示。
|
图 16 第2种假设,叠加模型理论计算与实验结果对比 |
分析计算值与实验的误差:
| $ \Delta {g_1} = 1.04\% ,\Delta {g_2} = 7.05\% ,\Delta {g_3} = 0.69\% ,\Delta {g_4} = 8.11\% ; $ |
| $ \Delta {\theta _1} = 1.15\% ,\Delta {\theta _2} = 32.87\% ,\Delta {\theta _3} = 14.47\% ,\Delta {\theta _4} = 8.94\% 。$ |
从实验得到的动态剪切模量和阻尼角随频率变化的趋势可以看出,κ=2/45时的曲线走势与其他振幅下的趋势不一致,特别是该振幅下阻尼角随频率变化的趋势。用上文所述的粘弹模型,不可能得到这样的变化趋势。所以,认为κ=2/45振幅下的实验数据,特别是阻尼角的数据不可用。其他振幅下,动态剪切模量随频率变化曲线与实验对比,误差都能控制在10%以内,阻尼角都能控制在15%以内,说明通过理论模型拟合的参数比较可靠。
4 粘弹塑性集成模型在ABAQUS中的实现及误差分析参照其他文献中将橡胶材料粘弹模型向ABAQUS材料参数转化的方法[10],将该橡胶材料粘弹塑性本构模型转化为ABAQUS软件中的材料参数。
如图 17中左图所示,笔者采用网格叠加的方法,将超弹、粘弹以及弹塑性单元集成到一个模型中。采用两层共节点的网格,分别赋予不同的材料。

|
图 17 ABAQUS材料实验模型 |
第1层网格赋予超弹和粘弹材料参数:
1) 超弹单元采用Mooney-Rivlin长效响应模型,C01=0.184, C10=0.046。
2) 粘弹单元采用时域PRONY级数形式来定义,即
| $ {g_1} = 0.0649,{\tau _1} = 0.0066; $ |
| $ {g_2} = 0.0981,{\tau _2} = 0.0296; $ |
| $ {g_3} = 0.2593,{\tau _3} = 9.077{\rm{e}} - 004。$ |
第2层网格赋予弹塑性材料参数(见表 2)。
| 表 2 ABAQUS中塑性单元材料参数定义(E=2.4 MPa) |
塑性单元的定义,需要把剪切变化到拉压,即
| $ E = 3G,\varepsilon = \kappa /\sqrt 3 ,\sigma = E \cdot \varepsilon = \sqrt 3 \tau 。$ |
在ABAQUS中建立有限元模型,切向加载不同振幅和频率的位移。记录作动端的位移和固定端的力,并转化为剪切应力和应变。
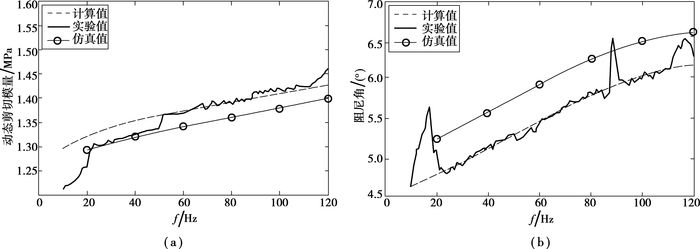
图 18为材料模型动态特性理论、仿真以及实验结果的对比。比较理论计算值和仿真值发现:动态剪切模量的理论计算值比仿真值大0.031 MPa;阻尼角的理论计算值比仿真值小0.424 5°。这是由于有限元中采用的基于机械硬化的塑性单元存在背应力现象导致的。为了提高仿真精度,应该在通过理论计算拟合材料参数的阶段,将动态剪切模量的目标值上调0.031 MPa,将阻尼角的目标值下调0.424 5°。
|
图 18 材料模型动态特性理论、仿真以及实验结果的对比 |
目标值修改后,按照之前假设2的方法,再做一次材料参数的拟合,得到的结果如下:
1) 超弹单元采用Mooney-Rivlin长效响应模型,C01=0.196 4, C10=0.091;
2) 粘弹单元采用时域PRONY级数形式来定义,即
| $ {g_1} = 0.0638,{\tau _1} = 0.0957; $ |
| $ {g_2} = 0.0899,{\tau _2} = 0.0105; $ |
| $ {g_3} = 0.2394,{\tau _3} = 9.5255{\rm{e}} - 004。$ |
3) 塑性单元,不改变,如表 2所示。
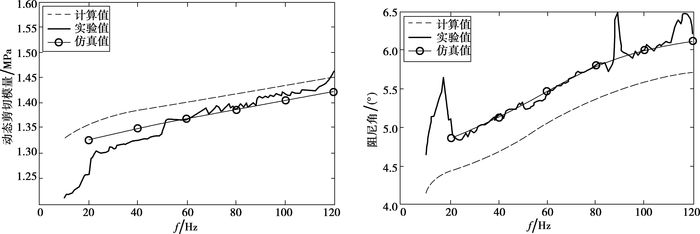
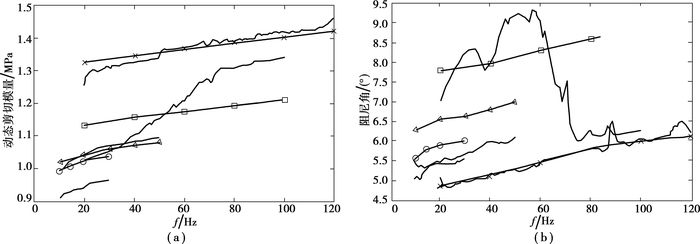
图 19为振幅κ=1/45工况下,修正后的理论计算、有限元以及实验结果的对比。可以看出,有限元仿真结果与实验贴合得非常好。同时,还对比了其他几个振幅工况下的有限元与实验结果如图 20所示。
|
图 19 振幅κ=1/45工况下,修正材料模型动态特性的理论、仿真以及实验结果的对比 |
|
图 20 修正后,材料模型动态特性的有限元与实验结果对比 |
动态剪切模量和阻尼角在不同振幅下,实验值与仿真值的误差如表 3所示。
| 表 3 各振幅工况下,材料模型动态特性有限元与实验结果对比 |
同样认为κ=2/45振幅下的实验数据不可用。其他振幅下,动态剪切模量随频率变化曲线与实验对比,误差都控制在10%以内,阻尼角都控制在16%以内,说明有限元模型比较可靠,可用于后续橡胶衬套以及悬架系统的分析。
5 结论1) 通过橡胶衬套的轴向实验,得到了橡胶材料的动态剪切模量和阻尼角,分析了其频率和振幅的相关性。
2) 用带屈服过程的塑性单元来描述橡胶材料的振幅相关性,提出了一种将弹性单元、粘弹单元和塑性单元集成的橡胶材料本构模型。
3) 把该理论模型转化为有限元模型,提出了有限元中塑性单元替代摩擦模型的方法。给出了塑性模型动特性理论计算方法,分析了塑性单元个数以及屈服点分布对橡胶材料集成模型的影响。
4) 该橡胶材料有限元模型的仿真结果与实验结果吻合较好。
5) 基于提出的橡胶材料本构模型,建立了橡胶衬套的有限元模型,结合悬架多体模型分析了衬套对悬架系统特性的影响,具有较高的实用价值。
| [1] | 于增亮. 轮毂电机驱动电动车悬架系统振动特性研究[D]. 上海: 同济大学博士学位论文, 2010. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=qcgc201404003&dbname=CJFD&dbcode=CJFQ |
| [2] | Slawomir D. Experiment-based modeling of cylindrical rubber bushings for the simulation of wheel suspension dynamic behavior[J]. Society of Automotive Engineers, 2000, 109: 78–85. |
| [3] | Sjöberg M, Kari L. Non-linear behavior of a rubber isolator system using fractional derivatives[J]. Vehicle System Dynamics, 2002, 37(3): 217–236. DOI:10.1076/vesd.37.3.217.3532 |
| [4] | Shaska K. The characterization of nonlinear viscoelastic isolators[D]. Michigan:Wayne State University, 2005. |
| [5] |
于增亮, 张立军, 罗鹰.
一种新的橡胶衬套半经验动力学模型[J]. 汽车技术, 2010(8): 6–11.
YU Zengliang, ZHANG Lijun, Luo Ying. A new rubber bushings semi-empirical kinetic model[J]. Automotive Technology, 2010(8): 6–11. (in Chinese) |
| [6] | Gil-Negretea N, Vinolasa J, Kari L. A simplified methodology to predict the dynamic stiffness of carbon-black filled rubber isolators using a finite element code[J]. Journal of Sound and Vibration, 2006, 296(4/5): 757–776. |
| [7] | Berg M. A non-linear rubber spring model for rail vehicle dynamics analysis[J]. Vehicle System Dynamics, 1998, 30(3/4): 197–212. |
| [8] | Berg M. A model for rubber springs in the dynamic analysis of rail vehicles[J]. Proceedings Institution of Mechanical Engineers, 1997, 211(2): 95–108. |
| [9] | Olsson A K. Finite element procedures in modeling the dynamic properties of rubber[D].Sweden:Lund University, 2007. |
| [10] |
潘晓明, 余俊, 杨钊, 等.
一种将线性粘弹微分型本构方程应用到ABAQUS的方法[J]. 华侨大学学报:自然科学版, 2010, 31(5): 570–575.
PAN Xiaoming, YU Jun, YANG Zhao, et al. Abaqus approach to the application of a differential type linear viscoelastic constitutive equation[J]. Journal of Huaqiao University:Natural Science, 2010, 31(5): 570–575. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

