2. 重庆大学 机械传动国家重点实验室, 重庆 400044
2. The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China
Power MEMS基于MEMS的微型动力能源系统,它通过利用燃烧化学反应能量,从而实现超高能量密度。采用液态烃类燃料的Power MEMS能量密度比当今最好的LiSO2电池高20~30倍,能满足远距离传输要求,在便携式能源系统领域有重要的研究价值[1]。MIT的Epstein[2]最早提出微型涡轮发动机概念,在微型流体力学、微燃烧等基础领域取得了很多进展,但仍未见完整样机的实际稳定运行。其他典型的Power MEMS研究还包括:汪克尔转子发动机[3]、超微型涡轮发动机和微型斯特林发动机(micro-stirling engine)[4]、NASA的微型蒸汽轮机[5]。相比其他Power MEMS,微型内燃机结构相对简单,热功转换原理成熟,更适合微型化制造。
顺应发展微动力能源系统的要求,微燃烧性能已成为国内外研究热点。新加坡Hua等[6-7]通过FLUENT模拟了H2/air预混气体在微型管道燃烧室的燃烧情况,发现只有燃烧室尺度大于绝热火焰厚度时气体才能稳定燃烧,当燃烧室尺度过小或者壁面热损失过大都会导致熄火。Norton等[8]将二维椭球型CFD微型燃烧器用来研究微型燃烧器尺度、导热、壁面厚度和材料、外部热损失条件等对燃烧特性和火焰稳定性的影响,发现壁面导热和厚度是决定逆流传热的重要因素,而逆流对点火和火焰稳定很必要,同时,导热和厚度是控制存在的热点的重要材料因素。Boyarkoa等[9]认为当燃烧室体积达到毫米级别的时候,表面积与体积的比值变大,微空间燃烧的热损失增加,易导致热淬息和基元淬息。冉景煜等[10]认为微空间燃烧应当通过表面催化过程得到促进。可见,对于微型内燃机,由于表面积体积比大,相对热损大,燃烧室热边界对微燃烧的影响非常大,所以在设计燃烧室时,需要特别注意包括燃烧室壁面参数在内的热边界对微燃烧的影响。
为了研究燃烧室热边界对微型内燃机微燃烧特性的影响以指导燃烧室设计,首先对微型燃烧室内的微流动过程进行分析,以确定适合微燃烧过程的仿真数学模型,并建立具体的仿真模型。再对仿真结果进行有效性分析,详细分析网格尺寸、时间步长、步长内最大计算步数3个关键建模因素对仿真精度的影响,以确定以上建模参数。最后,详细分析散热系数、壁面厚度和材料3个参数对瞬态燃烧过程的影响。
1 层流有限速率模型及甲醇氧化机理 1.1 层流有限速率模型微型发动机尺寸较小,留给缸内燃料燃烧时间较短,要求燃料具有较快的燃烧速度。低碳烷烃甲醇具有较大的层流火焰传播速度(0.327 m/s),且常温下为液体,便于充装,适合于用作微型发动机燃料[11]。分析微型燃烧室内混合气体流动状态,发现雷诺数为568~1 840(随转速变化),流动状态为层流。对于层流预混燃烧,燃烧反应速率受化学反应控制。因此,将层流有限速率模型应用于微型内燃机甲醇预混瞬态燃烧过程的数值仿真,该模型能够准确预测缸内燃烧各组分的变化。
仿真控制方程包括质量守恒方程、动量守恒方程、能量守恒方程和组分质量守恒方程,其守恒方程通用形式为
| $\frac{\partial }{{\partial t}}\left( {\rho \phi } \right) + \nabla \cdot \left( {\rho \nu \phi } \right) = \nabla \cdot \left( {{\mathit{\Gamma }_\phi }\nabla \phi } \right) + S,$ | (1) |
式中,φ为通用求解变量,Γφ为广义扩散系数,S为广义源项, ρ为混合物密度,v为速度,Δ为散度。在特定方程中具体代表如表 1所示。
| 表 1 方程符号代表的具体意义 |
表 1中,μ为气体粘度,k为气体导热系数,cp为气体比热容,T为气体温度,Yi为组分质量分数,Di, m为组分扩散系数,Ri为组分化学反应源项。
在求解组分i的质量守恒方程时,层流有限速率模型采用Arrhenius公式计算化学反应源项。组分i的化学反应净源项通过有组分i参加的Nr个化学反应的Arrhenius反应源的和计算有
| ${R_i} = {M_{w,i}}\sum\limits_{i = 1}^{{N_r}} {{{\hat R}_{i,r}}} ,$ | (2) |
式中,Mw, i是组分i的分子量,
| $\sum\limits_{i=1}^{N}{{{{{\nu }'}}_{i,r}}}{{M}_{i}}\underset{{{k}_{b,r}}}{\overset{{{k}_{f,r}}}{\rightleftharpoons}}\sum\limits_{i=1}^{N}{{{{{\nu }''}}_{i,r}}}{{M}_{i}},$ | (3) |
式中,N为系统中化学组分数目,ν′i, r为反应r中反应物i的化学计量系数,ν″i, r为反应r中生成物i的化学计量系数,Mi为组分i的符号,kf, r为反应r的正向速率常数,kb, r为反应r的逆向速率常数。
第r个反应中,组分i的产生或分解摩尔速度为
| ${{{\hat{R}}}_{i,r}}=\mathit{\Gamma }\left( {{{{\nu }''}}_{i,r}}-{{{{\nu }'}}_{i,r}} \right)\left( {{k}_{f,r}}\prod\limits_{j=1}^{{{N}_{r}}}{\left[ {{C}_{j,r}} \right]{{{{\eta }'}}_{j,r}}-{{k}_{b,r}}\prod\limits_{j=1}^{{{N}_{r}}}{\left[ {{C}_{j,r}} \right]{{{{\eta }''}}_{j,r}}}} \right),$ | (4) |
式中,Nr为反应r的化学组分数目,Cj, r为反应r中每种反应物或生成物j的摩尔浓度,η′j, r为反应r中每种反应物或生成物j的正向反应速度指数,η″j, r为反应r中每种反应物或生成物j的逆向反应速度指数,Γ为第三体对反应速率的净影响。反应r的正向速率常数kf, r通过Arrhenius公式计算为
| ${{k}_{f,r}}={{A}_{r}}{{T}^{{{\beta }_{r}}}}{{\rm{e}}^{\frac{-{{E}_{r}}}{RT}}}$ | (5) |
式中,Ar为指数前因子,βr为温度指数,Er为反应活化能,R为气体常数。逆向速率常数kb, r为
| ${{k}_{b,r}}=\frac{{{k}_{f,r}}}{{{k}_{r}}},$ | (6) |
式中kr为平衡常数。对于反应速率常数基于压力变化的处理采用Troe方法。
1.2 详细甲醇氧化反应机理早期,Bowman[12]、Held等[13]、Westbrook等[14]分别基于实验构建了甲醇氧化的详细反应机理,但上述机理都由于缺乏基元反应数据,在描述甲醇反应过程中存在较大误差。Grotheer机理能够用于模拟层流火焰速度和火花点火发动机中的自燃。Grotheer等[15]发现了CH3OH与OH反应生成CH2OH和CH3O的比率对火焰传播速度有很大的影响。Li等[16]以Held和Dryer机理为基础, 采用部分新的反应速率常数和热力学数据, 利用CO /H2O /H2/O2、CH2O、CH3OH的反应机理分级构建了一个甲醇氧化详细反应机理, 与Held和Dryer机理相比,该机理更适用范围更宽广。
仿真采用Li机理,共84步基元反应,17个组分。甲醇燃烧时, 首先与活性基OH、HO2、H、O发生脱氢反应, 生成CH2OH和CH3O,接着CH2OH和CH3O继续发生脱氢和高温裂解反应生成CH2O, CH2O与活性基发生脱氢反应生成HCO。HCO再通过脱氢和热裂解反应生成CO。最后CO被氧化生成最终产物CO2。另外再加上高温NO热生成机理。
2 微燃烧过程仿真模型建立仿真对象为一款微型二冲程活塞式内燃机,缸径10.8 mm, 行程10 mm,压缩比7.6。甲醇燃料燃点较高,所以采用电热丝助燃点火。燃烧室由下半部的圆柱体的上半部的圆锥体构成,助燃热丝位于燃烧室中心,故燃烧室结构中心轴对称。仿真从进气结束的上止点前105 ℃A开始,结束于开始排气的上止点后105 ℃A。由于仿真时缸内处于封闭状态,此时缸内流场主要在径向和轴向上变化,忽略进排气流动对流场初始条件的影响,这里假定缸内流场轴对称。并且仿真时采用详细化学反应机理,所需计算时间较长,为了节约计算成本,这里只对缸内一个二维轴对称平面内的流场进行仿真。对燃烧室建立二维轴对称几何模型,燃烧室几何空间由顶面、热丝热头、壁面、对称轴和表现为可移动边界的活塞构成。初始状态活塞距顶面距离为S0,终止状态为S1,对于任一时刻t,活塞行程St由式(8)确定:
| ${S_t} - {S_0} = L + \frac{L}{2}(1 - {\rm{cos}}{\theta _{\rm{t}}}) - \sqrt {{L^2} - \frac{{{L^2}}}{4}{\rm{si}}{{\rm{n}}^{\rm{2}}}{\theta _{\rm{t}}}} ,$ | (8) |
式中,冲程L=S1-S0,无量纲时间θt=
计算域采用四边形和三角形混合网格方案划分,网格总数约2 100。采用动态分层动网格技术划分动网格,压缩合并因子取为0.1,分割因子取为0.4。对于微型发动机,通过分析发现由于壁面非常薄,很难在壁面上加工出适合于准确测量汽缸内壁面温度的孔,所以很难获得准确的汽缸内壁面温度。并且通过初步仿真分析发现,由于汽缸半径只有约5 mm,仿真时设置的壁面温度对缸内燃烧性能影响非常大,远大于宏观机组的情况。综合考虑以上原因,相对较为合理的处理是对壁面设置第三类热边界条件,即平均换热系数和环境温度。而固体材料内部导热则按一维流假设处理。燃烧室外壁面平均对流换热系数通过强制横掠管外对流换热关系式Nu=CRenPr
数值仿真结果误差主要由数值误差和建模误差组成,数值误差主要由网格产生的离散误差和时间步长产生的离散误差以及控制方程离散所产生的截断误差组成。在此就控制离散误差展开详细讨论。
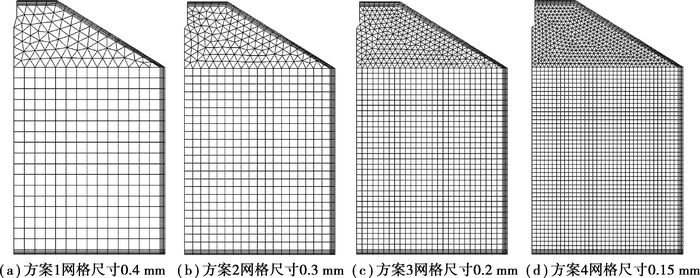
3.1 网格密度对仿真的影响及网格无关性分析网格密度是影响仿真计算的重要因素,一方面如果网格密度过小,则会增加离散误差;另一方面,随网格密度的增加,无反应流场的计算时间和化学反应计算总时间都将急速增加,增加计算成本。为了找到既满足计算精度,又具有相对较小计算成本的网格划分方案,对不同的网格密度方案进行分析。图 1显示了4个网格方案,方案1网格密度最小,网格尺寸为0.4 mm,方案4网格密度最大,网格尺寸为0.15 mm,计算中所有参数均保持相同。计算发现方案1~方案4在一台P4 2.5G CPU/3.5G DDR的计算机配置下所需的计算时间分别为10、12、16、23 h,可见随网格数量的增加,计算时间加速增加,影响很大。
|
图 1 网格模型方案 |
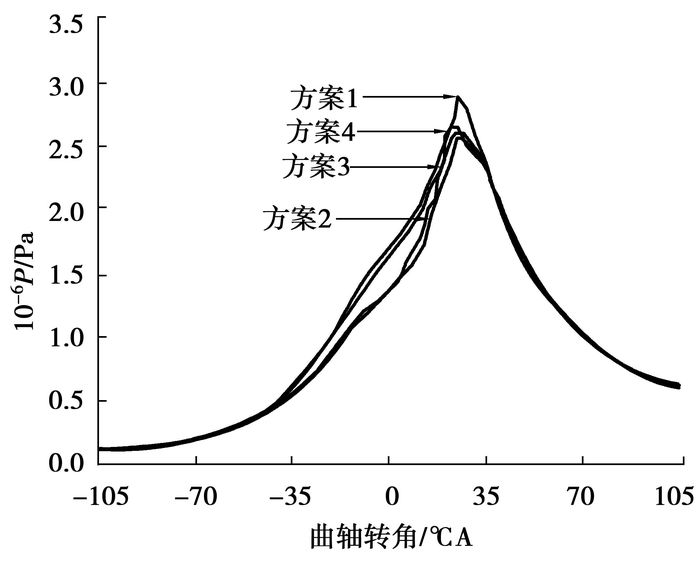
图 2显示的是不同网格密度下的缸内压力对比图。缸压用P表示,由图可以看到方案1和方案2的着火时刻点稍微晚一些,压力升高率小于另外两个方案,而方案3和方案4的缸压曲线基本一致。这主要是由于方案1和方案2的网格密度相对较小,因此,近壁区网格内的混合气相对较多,受到壁面低温影响的区域相对较大,所以缸内平均温度相对较低,着火点略有滞后。可见当网格尺寸减小到0.2 mm以后,再进一步减小25%并不能带来解的明显变化,可认为此时解具有网格独立性,综合考虑计算时间成本,最后取网格尺寸为0.2 mm,即方案3。
|
图 2 不同网格下缸内压力比较 |
类似于空间差分的网格密度,时间尺度差分的步长也对计算有较大的影响。在多维流场与化学反应耦合计算中,通常采用“反应流动”模式将流动与化学反应解耦。首先,在通过chemkin软件工具进行化学反应计算时假定各个单元的体积在一个时间步内不变,接着将计算结果导入多维计算中用于各单元流场计算,直到进入下一个时间步。可见时间步长将同时影响流场和化学反应计算,理论上要求步长无限小,以使计算的结果逼近于准确值。
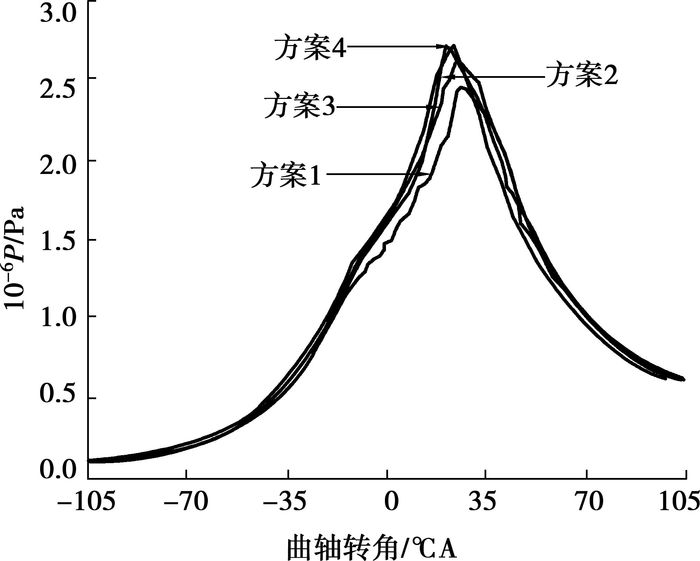
图 3显示了4个步长方案下的缸内压力计算结果,方案1时间步长为0.4 ℃A,方案2为0.2 ℃A,方案3为0.1 ℃A,方案4为0.05 ℃A。可见时间步长较大时,压力升高率相对较小,着火点也有所滞后,当步长减小到0.1 ℃A时,再继续缩减对缸内压力影响较小。而所用计算时间上,0.4 ℃A步长时需要9 h,0.2 ℃A步长时需要16 h,缩减到0.05 ℃A时时间增加到25 h,可见时间成本增加很大。综合以上因素考虑,最后选取的方案为0.1 ℃A,即方案3。
|
图 3 不同步长下缸内压力比较 |
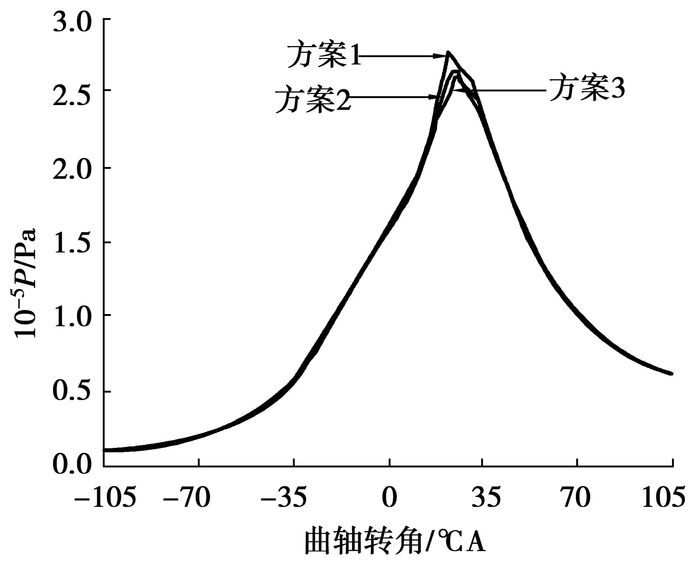
当确定了时间步长后,步长内的最大迭代步数将会影响时间步长内的计算精度,从而影响下一时间步的初始值,进而影响整个计算结果。图 4显示了当步长为0.1 ℃A时,最大迭代步数分别为方案1的50步、方案2的100步和方案3的150步的缸内压力对比,计算时将收敛指数设置为较小的判断值,以使3个案例下都能算到最大步数。由图可见,主要在上止点附近有较大差别,当步数从100增加到150时,差异已经比较小,综合考虑,最后选取迭代步数为100,即方案2。
|
图 4 不同计算步数下缸内压力比较 |
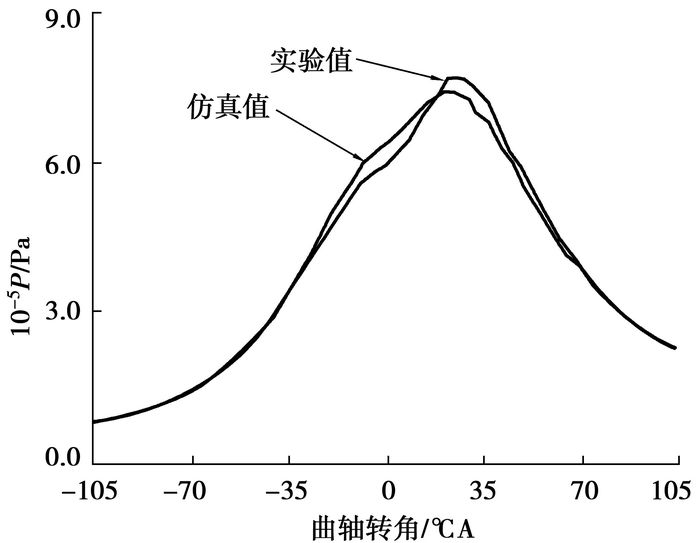
在上述讨论结果的基础上,将仿真结果与实验结果进行对比,对比工况为初始压力0.69 atm, 初始温度370 K,转速6 000 r/min,当量比1.8,缸径10.8 mm,压缩比7.6,图 5显示仿真结果与实验结果比较吻合,说明建模误差较小。综合上述比较和分析,仿真结果有效。
|
图 5 仿真与实验结果对比 |
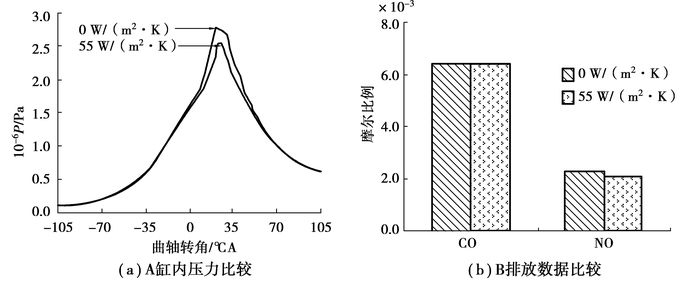
对于微型发动机,由于缸径非常小,并且表面积体积比比较大,所以缸壁面对外环境的散热是影响燃烧的重要因素。为了考察散热对燃烧性能的具体影响,仿真了不同换热系数下的燃烧。图 6为不同散热系数下的燃烧性能图,工况为初始压力1 atm, 初始温度370 K,转速为5 000 r/min,当量比1.0,压缩比7.6。从图中可以发现,当换热系数从0增加到55 W/(m2·K)时,平均压力升高率减小,着火点稍有滞后,最高压力值下降了2个大气压。图中还显示CO排放基本一致,NO排放随散热量的增大而有所下降。这主要是由于NO生成量受缸内温度决定,所以会有所下降。
|
图 6 不同散热系数下燃烧与排放对比 |
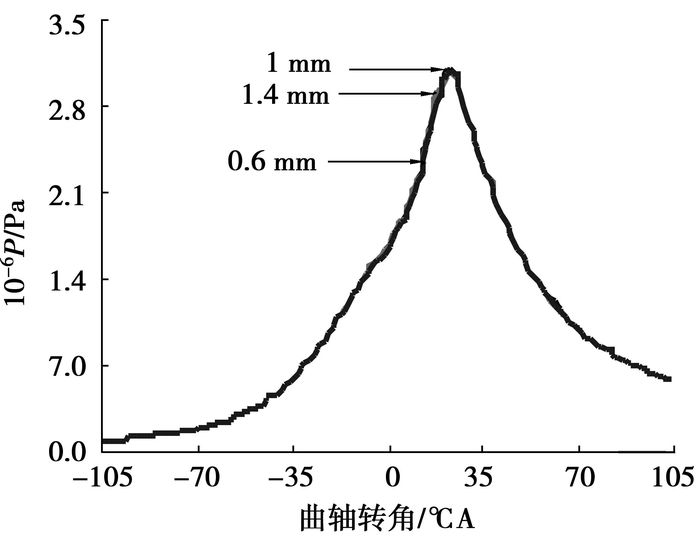
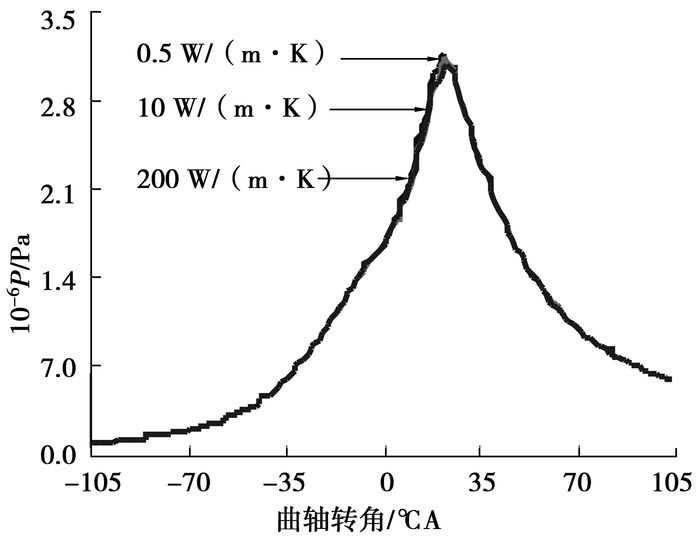
图 7和图 8分别为不同缸壁厚度和材料下的燃烧性能图,工况为初始压力1 atm, 初始温度370 K,转速为4 000 r/min,当量比1.0,压缩比7.6。从图 7和图 8发现,对于微型发动机,缸壁面厚度从0.5 mm增加到1.4 mm和壁面导热系数从0.5 W/(m·K)增加到200 W/(m·K)时,缸内压力变化非常小,可认为燃烧过程差别不大。这主要是由于在热量从缸内传出到外界环境热流路径中,主要传热热阻是外壁面与环境之间的对流换热热阻,所以缸壁面参数变动对总的散热影响不大,从而对燃烧过程影响很小。
|
图 7 不同壁面厚度下缸内压力比较 |
|
图 8 不同壁面材料下缸内压力比较 |
分析壁厚对散热的影响,增加壁面厚度将引起壁面导热热阻增大,从而减小散热,但前提必须是壁面导热热阻大于壁面与环境间对流换热热阻或者是两者大小相当,此时改动壁厚对散热影响才比较明显。所以,设计壁厚时除了考虑抗缸压强度性能以外,还需要考虑壁面与外环境的散热以及材料的耐高温特性。
对于壁面材料导热性能的选取,同样需要参考壁面与外环境间的散热性能。当选用导热系数较小的材料时,壁面导热热阻增大,从而减小散热,但前提也必须是壁面导热热阻大于壁面与环境间对流换热热阻或者是两者大小相当,此时修改壁面材料和厚度对整个散热和燃烧性能的影响会比较明显,设计有意义。否则,如文中仿真结果,基本不需要考虑壁面参数对散热的影响。
5 结论1) 分析了微型燃烧室内的微燃烧过程,指出其内部为层流预混燃烧,燃烧反应速率受化学反应控制。由此确定了对微燃烧过程进行仿真的数学模型为层流有限速率模型,并且进一步建立了具体的仿真模型。
2) 对仿真结果进行了有效性分析,详细讨论了网格尺寸、时间步长、步长内最大计算步数3个关键建模因素对仿真结果的影响。由此确定了以上3个建模参数,最后结果表明,仿真结果与实验结果比较吻合,仿真结果有效。
3) 散热系数对燃烧特性有较明显的影响。散热系数从0增加到55 W/(m2·K)时,平均压力升高率减小,着火点延后,最高压力值下降了2个大气压,散热系数通过影响燃烧室内的温度从而影响NO排放特性。
4) 壁面厚度和壁面材料对燃烧特性影响很小。通过进一步分析,揭示了燃烧特性对壁面厚度和材料不敏感的具体原因,由于在热量从缸内传出到外界环境的热流路径中,主要传热热阻是外壁面与环境之间的对流换热热阻,故缸壁面参数变动对燃烧特性影响很小。分析还指出当壁面热阻大于外壁面和环境之间的对流换热热阻或者是两者大小相当时,需要特别关注壁面参数的设计。
| [1] | Chou S K, Yang W M, Chua K J, et al. Development of micro power generators-A review[J]. Applied Energy, 2011, 88(1): 1–16. DOI:10.1016/j.apenergy.2010.07.010 |
| [2] | Epstein A H. Millimeter-scale, micro-electro-mechanical systems gas turbine engines[J]. Journal of Engineering for Gas Turbines and Power, 2004, 126(2): 205–226. DOI:10.1115/1.1739245 |
| [3] | Fernandez-Pello A C, Pisano A P, Fu K, et al. MEMS rotary engine power system[J]. 電気学会論文誌E (センサ·マイクロマシン部門誌), 2003, 123(9): 326–330. |
| [4] | Matsuo E, Yoshiki H, Nngashima T, et al. The development of the ultra micro gas turbines[J]. Journal of the Japan Institute of Energy, 2005, 84(3): 192–199. |
| [5] | Fréchette L G, Lee C, Arslan S, et al. Design of a microfabricated Rankine cycle steam turbine for power generation[C]//ASME 2003 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, 2003:335-344. |
| [6] | Hua J, Wu M, Kumar K. Numerical simulation of the combustion of hydrogen-air mixture in micro-scaled chambers. Part Ⅰ:fundamental study[J]. Chemical Engineering Science, 2005, 60(13): 3497–3506. DOI:10.1016/j.ces.2005.01.041 |
| [7] | Hua J, Wu M, Kumar K. Numerical simulation of the combustion of hydrogen-air mixture in micro-scaled chambers Part Ⅱ:CFD analysis for a micro-combustor[J]. Chemical Engineering Science, 2005, 60(13): 3507–3515. DOI:10.1016/j.ces.2005.01.042 |
| [8] | Norton D G, Vlachos D G. Combustion characteristics and flame stability at the microscale:a CFD study of premixed methane/air mixtures[J]. Chemical Engineering Science, 2003, 58(21): 4871–4882. DOI:10.1016/j.ces.2002.12.005 |
| [9] | Boyarko G A, Sung C J, Schneider S J. Catalyzed combustion of hydrogen-oxygen in platinum tubes for micro-propulsion applications[J]. Proceedings of the Combustion Institute, 2005, 30(2): 2481–2488. DOI:10.1016/j.proci.2004.08.203 |
| [10] |
冉景煜, 秦昌雷, 吴晟.
壁面参数对甲烷微尺度催化燃烧的影响[J]. 重庆大学学报, 2012, 35(2): 1–9.
RAN Jingyu, QIN Changlei, WU Shen. The effects of wall parameters on CH4 catalytic combustion in micro-channel[J]. Journal of Chongqing University, 2012, 35(2): 1–9. DOI:10.11835/j.issn.1674-4764.2012.02.001 (in Chinese) |
| [11] | 蒋德明, 黄佐华. 内燃机替代燃料燃烧学[M]. 西安: 西安交通大学出版社, 2007. |
| [12] | Bowman C T. A shock-tube investigation of the high-temperature oxidation of methanol[J]. Combustion and Flame, 1975, 25: 343–354. DOI:10.1016/0010-2180(75)90106-6 |
| [13] | Held T J, Dryer F L. A comprehensive mechanism for methanol oxidation[J]. International Journal of Chemical Kinetics, 1998, 30(11): 805–830. DOI:10.1002/(ISSN)1097-4601 |
| [14] | Westbrook C K, Dryer F L. A comprehensive mechanism for methanol oxidation[J]. Combustion Science and Technology, 1979, 20(3-4): 125–140. DOI:10.1080/00102207908946902 |
| [15] | Grotheer H H, Kelm S, Driver H S T, et al. Elementary reactions in the methanol oxidation system. Part Ⅰ:establishment of the mechanism and modelling of laminar burning velocities[J]. Berichte der Bunsengesellschaft für physikalische Chemie, 1992, 96(10): 1360–1376. DOI:10.1002/bbpc.v96:10 |
| [16] | Li J, Zhao Z, Kazakov A, et al. A comprehensive kinetic mechanism for CO, CH2O, and CH3OH combustion[J]. International Journal of Chemical Kinetics, 2007, 39(3): 109–136. DOI:10.1002/kin.20218 |
 2014, Vol. 37
2014, Vol. 37

